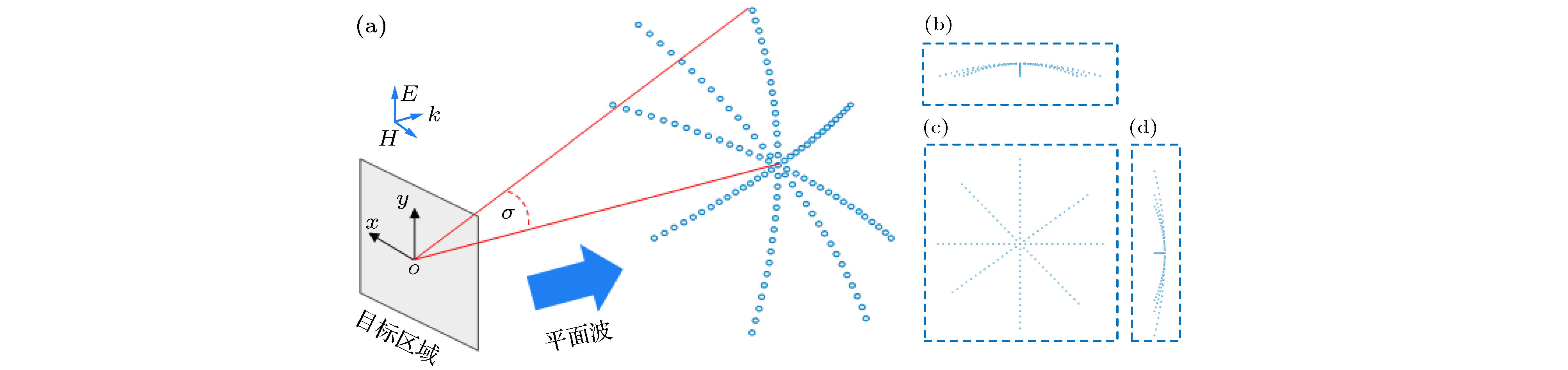
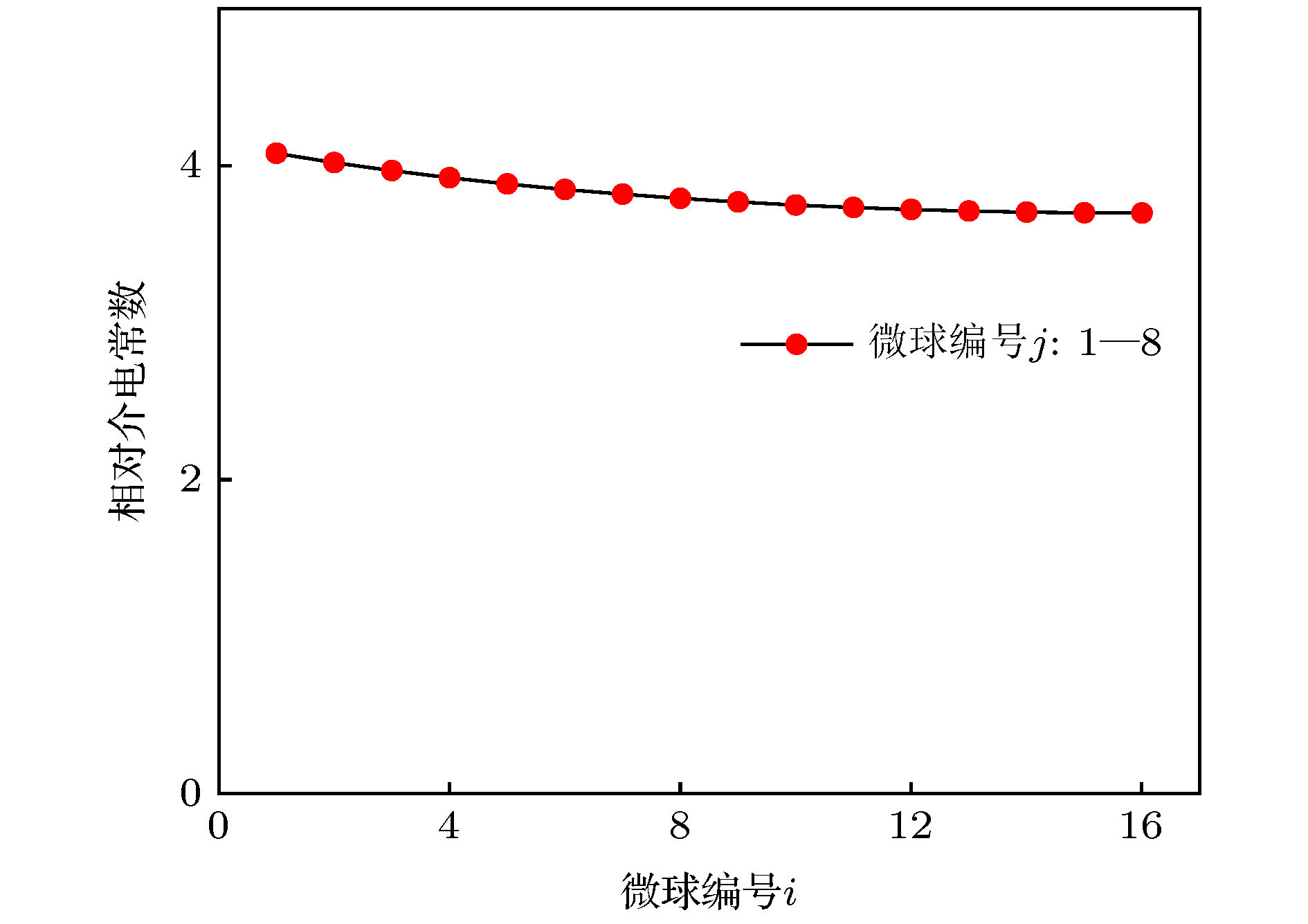
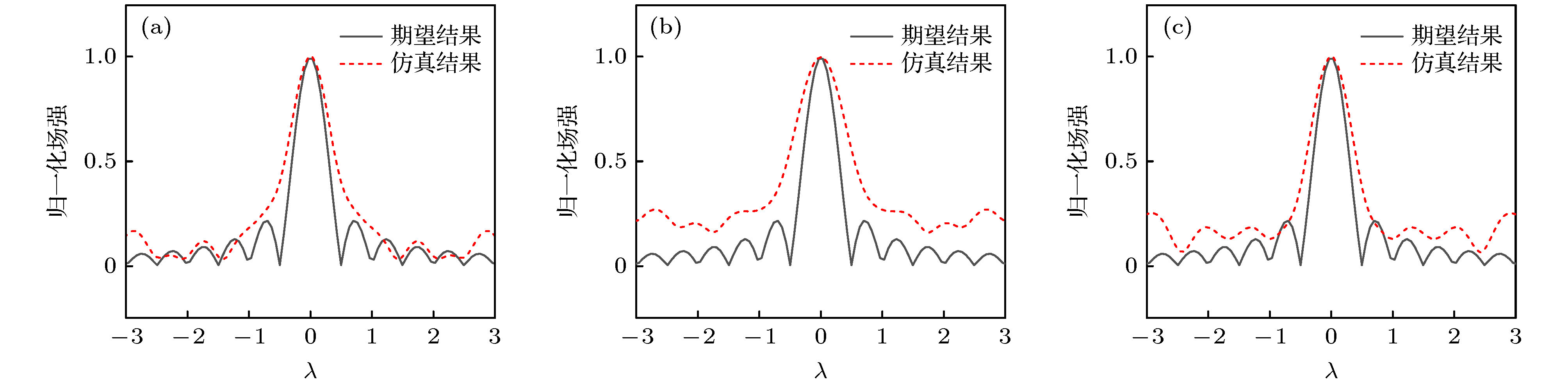
-
It is a novel and interesting idea to inversely design the scattering structure with the desired scattering field intensity distribution in a given target area as the known information. The inverse design method proposed in this paper does not need to be optimized, and the spatial distribution and dielectric constant distribution of the micro-scatterer array can be quickly analytically calculated according to the desired scattering field intensity in the target area. First, based on the spatial Fourier transform and angular spectrum transformation, the plane wave sources required in all directions are inversely obtained from the electric field intensity distribution required in the target area. Then, based on the theory of induced source, a method of irradiating the array of all-dielectric micro-scatterers with incident electromagnetic field to generate the required plane wave source is proposed. The scattering fields generated by these micro-scatterers will be superimposed on the target area to achieve the desired scattering field strength intensity. Finally, according to the proposed inverse design theory model, a specific three-dimensional (3D) design is carried out. In the 3D example, we study the scattering field intensity distribution of the point-focused shape of the square surface target area, and show an all-dielectric micro-sphere distribution design. Its spatial distribution and permittivity distribution are both obtained through the rapid analytical calculation of the desired scattered field intensity shape in the target area. Finally, based on the principle of linear superposition, we quickly and easily generate the complex shapes of “I”, “T”, and “X” in the target area. The satisfactory results of full-wave simulation show that the proposed inverse design method is effective and feasible.
-
Keywords:
- inverse design /
- scattering field intensity shaping /
- spatial spectrum
[1] Fink M, Prada C, Wu F, Cassereau D 1989 Proceedings, IEEE Ultrasonics Symposium Montreal, Canada, October 3−6, 1989 p681
[2] Azar L, Shi Y, Wooh S C 2000 NDT&E Int. 33 189
Google Scholar
[3] Zhao X Y, Gang T 2008 Ultrasonics 49 126
Google Scholar
[4] 张碧星, 王文龙 2008 物理学报 57 3613
Google Scholar
Zhang B X, Wang W L 2008 Acta Phys. Sin. 57 3613
Google Scholar
[5] 郑莉, 郭建中 2016 物理学报 65 044305
Google Scholar
Zheng L, Guo J Z 2016 Acta Phys. Sin. 65 044305
Google Scholar
[6] Shan L, Wen G Y 2014 IEEE Trans. Antennas Propag. 62 5565
Google Scholar
[7] Wang X Y, Yang G M, Wen G Y 2014 Microwave. Opt. Technol. Lett. 56 2464
Google Scholar
[8] Nepa P, Buffi A 2017 IEEE Antennas Propag. Mag. 59 42
Google Scholar
[9] Elmer M, Jeffs B D, Warnick K F, Fisher J R, Norrod R D 2012 IEEE Trans. Antennas Propag. 60 903
Google Scholar
[10] Guo S, Zhao D, Wang B Z 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Guangzhou, China, May 19−22, 2019 p1
[11] Zhao D, Zhu M 2016 IEEE Antennas Wirel. Propag. Lett. 1 5
Google Scholar
[12] Zhao D, Guo F, Guo S, Wang B Z 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Chengdu, China, May 7−11, 2018 p1
[13] Bellizzi G G, Crocco L, Iero D A M, Isernia T 2017 International Workshop on Antenna Technology: Small Antennas, Innovative Structures, and Applications (iWAT) Athens, March 1−3, 2017 p162
[14] Bellizzi G G, Bevacqua M T, Crocco L, Isernia T 2018 IEEE Trans. Antennas Propag. 66 4380
Google Scholar
[15] Alu A 2009 Phys. Rev. B 80 245115
Google Scholar
[16] Yu N, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[17] Pfeiffer C, Grbic A 2013 Phys. Rev. Lett. 110 197401
Google Scholar
[18] Grbic A, Jiang L, Merlin R 2008 Science 320 511
Google Scholar
[19] Imani M F, Grbic A 2013 IEEE Trans. Antennas Propag. 61 5425
Google Scholar
[20] Grbic A, Merlin R, Thomas E M, Imani M F 2011 Proceedings of the IEEE 99 1806
Google Scholar
[21] Khorasaninejad M, Chen W T, Devlin R C, Oh J, Zhu A.Y, Capasso F 2016 Science 352 1190
Google Scholar
[22] Li L, Liu H, Zhang H, Xue W 2018 IEEE Trans. Ind. Electron. 65 3230
Google Scholar
[23] Yu S, Liu H, Li L 2019 IEEE Trans. Ind. Electron. 66 3993
Google Scholar
[24] Chen X D 2018 Computational Methods for Electromagnetic Inverse Scattering (Hoboken: Wiley-IEEE Press) p24
[25] Kong J A 1990 Electromagnetic Wave Theory (New York: Wiley-Interscience) pp482−483
-
图 1 逆向设计示意图
Figure 1. Schematic diagram of inverse design.
图 2 微球阵列设计示意图 (a) 三维视角图; (b)俯视图; (c)正视图; (d)侧视图
Figure 2. Schematic of micro-sphere array design: (a) 3-D view; (b) top view; (c) front view; (d) side view.
图 3 微球相对介电常数分布
Figure 3. Spheres relative permittivity of array distribution.
图 4 目标区域归一化点聚焦形状散射场分布图 (a) 三维视角图; (b) 俯视图
Figure 4. Normalized scattering field distribution of focused shape in target area: (a) 3-D view; (b) top view.
图 5 目标区域三条线上的归一化散射场分布图 (a) y = 0处场分布; (b) x = 0处分布; (c) y = x处场分布
Figure 5. Normalized scattering field distribution on three special lines in target area: (a) A cut view in y = 0; (b) a cut view in x = 0; (c) a cut view in y = x.
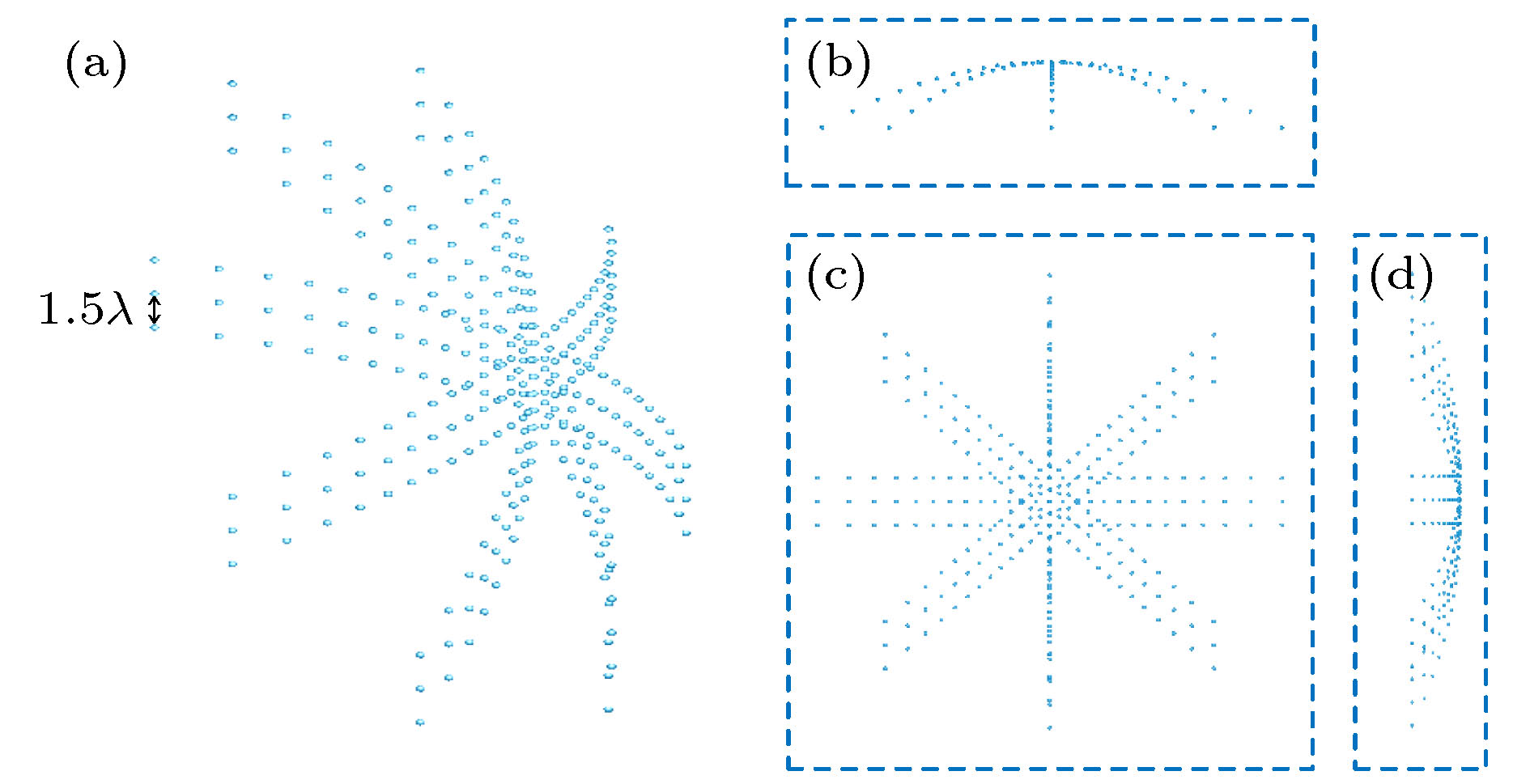
图 6 目标区域归一化复杂形状散射场分布图 (a) 相对原点沿向x方向右平移沿z方向上平移2
${\lambda _0}$ 的点聚焦形状散射场; (b) “I”形状; (c) “T”形状; (d) “X”-形状Figure 6. Normalized scattering field intensity distribution of complex shape in target area: (a) focused shaped field moving 2
${\lambda _0}$ to the right and top relative to the origin; (b) “I”-shaped; (c) “T”-shaped; (d) “X”-shaped.
图 7 “I”形散射场分布的微散射体阵列示意图 (a) 三维视角图; (b)俯视图; (c)正视图; (d)侧视图
Figure 7. Schematic of micro-sphere array design with “I”-shaped: (a) 3-D view; (b) top view; (c) front view; (d) side view.
-
[1] Fink M, Prada C, Wu F, Cassereau D 1989 Proceedings, IEEE Ultrasonics Symposium Montreal, Canada, October 3−6, 1989 p681
[2] Azar L, Shi Y, Wooh S C 2000 NDT&E Int. 33 189
Google Scholar
[3] Zhao X Y, Gang T 2008 Ultrasonics 49 126
Google Scholar
[4] 张碧星, 王文龙 2008 物理学报 57 3613
Google Scholar
Zhang B X, Wang W L 2008 Acta Phys. Sin. 57 3613
Google Scholar
[5] 郑莉, 郭建中 2016 物理学报 65 044305
Google Scholar
Zheng L, Guo J Z 2016 Acta Phys. Sin. 65 044305
Google Scholar
[6] Shan L, Wen G Y 2014 IEEE Trans. Antennas Propag. 62 5565
Google Scholar
[7] Wang X Y, Yang G M, Wen G Y 2014 Microwave. Opt. Technol. Lett. 56 2464
Google Scholar
[8] Nepa P, Buffi A 2017 IEEE Antennas Propag. Mag. 59 42
Google Scholar
[9] Elmer M, Jeffs B D, Warnick K F, Fisher J R, Norrod R D 2012 IEEE Trans. Antennas Propag. 60 903
Google Scholar
[10] Guo S, Zhao D, Wang B Z 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Guangzhou, China, May 19−22, 2019 p1
[11] Zhao D, Zhu M 2016 IEEE Antennas Wirel. Propag. Lett. 1 5
Google Scholar
[12] Zhao D, Guo F, Guo S, Wang B Z 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Chengdu, China, May 7−11, 2018 p1
[13] Bellizzi G G, Crocco L, Iero D A M, Isernia T 2017 International Workshop on Antenna Technology: Small Antennas, Innovative Structures, and Applications (iWAT) Athens, March 1−3, 2017 p162
[14] Bellizzi G G, Bevacqua M T, Crocco L, Isernia T 2018 IEEE Trans. Antennas Propag. 66 4380
Google Scholar
[15] Alu A 2009 Phys. Rev. B 80 245115
Google Scholar
[16] Yu N, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[17] Pfeiffer C, Grbic A 2013 Phys. Rev. Lett. 110 197401
Google Scholar
[18] Grbic A, Jiang L, Merlin R 2008 Science 320 511
Google Scholar
[19] Imani M F, Grbic A 2013 IEEE Trans. Antennas Propag. 61 5425
Google Scholar
[20] Grbic A, Merlin R, Thomas E M, Imani M F 2011 Proceedings of the IEEE 99 1806
Google Scholar
[21] Khorasaninejad M, Chen W T, Devlin R C, Oh J, Zhu A.Y, Capasso F 2016 Science 352 1190
Google Scholar
[22] Li L, Liu H, Zhang H, Xue W 2018 IEEE Trans. Ind. Electron. 65 3230
Google Scholar
[23] Yu S, Liu H, Li L 2019 IEEE Trans. Ind. Electron. 66 3993
Google Scholar
[24] Chen X D 2018 Computational Methods for Electromagnetic Inverse Scattering (Hoboken: Wiley-IEEE Press) p24
[25] Kong J A 1990 Electromagnetic Wave Theory (New York: Wiley-Interscience) pp482−483
DownLoad:
Catalog
Metrics
- Abstract views: 6766
- PDF Downloads: 121
- Cited By: 0
