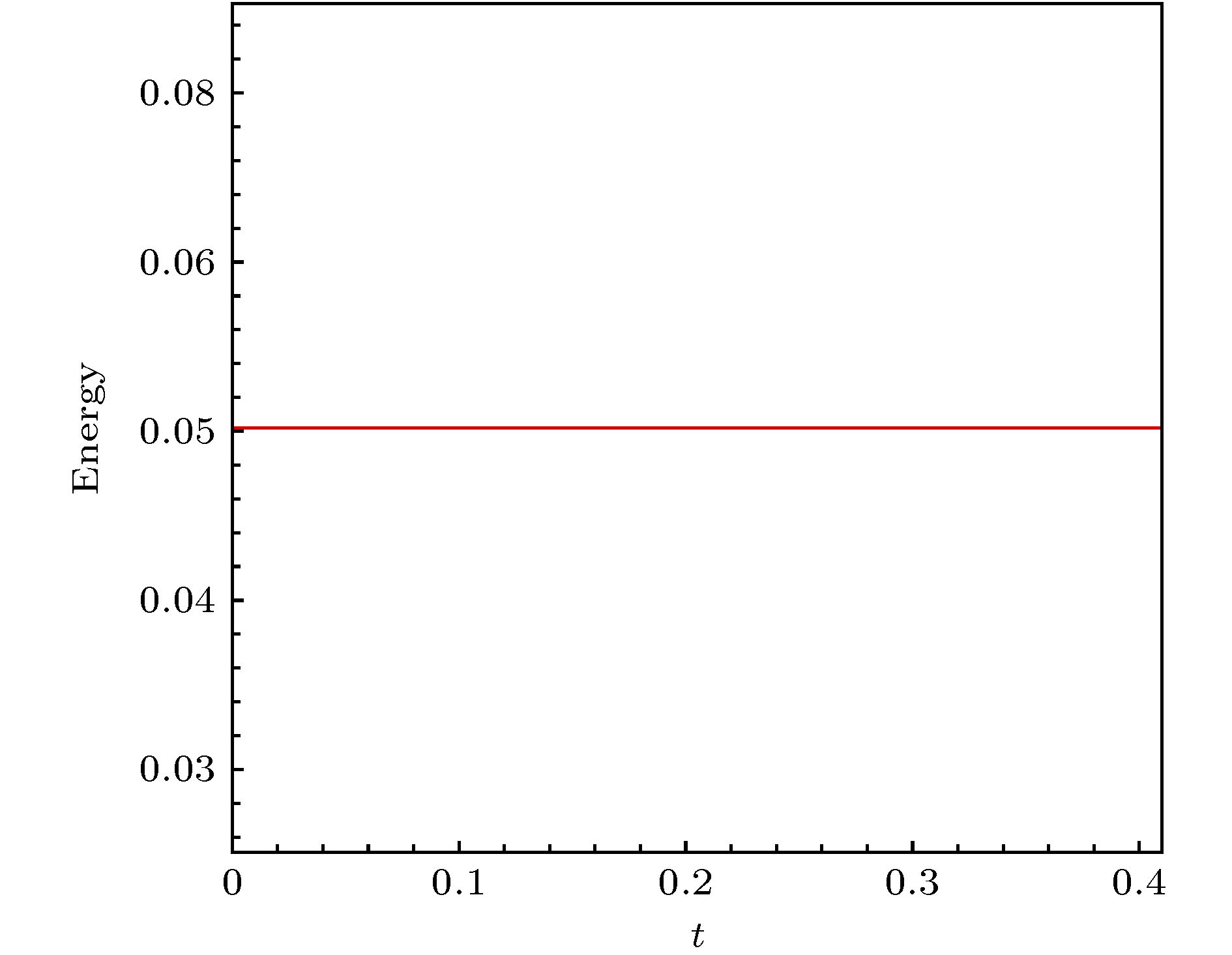
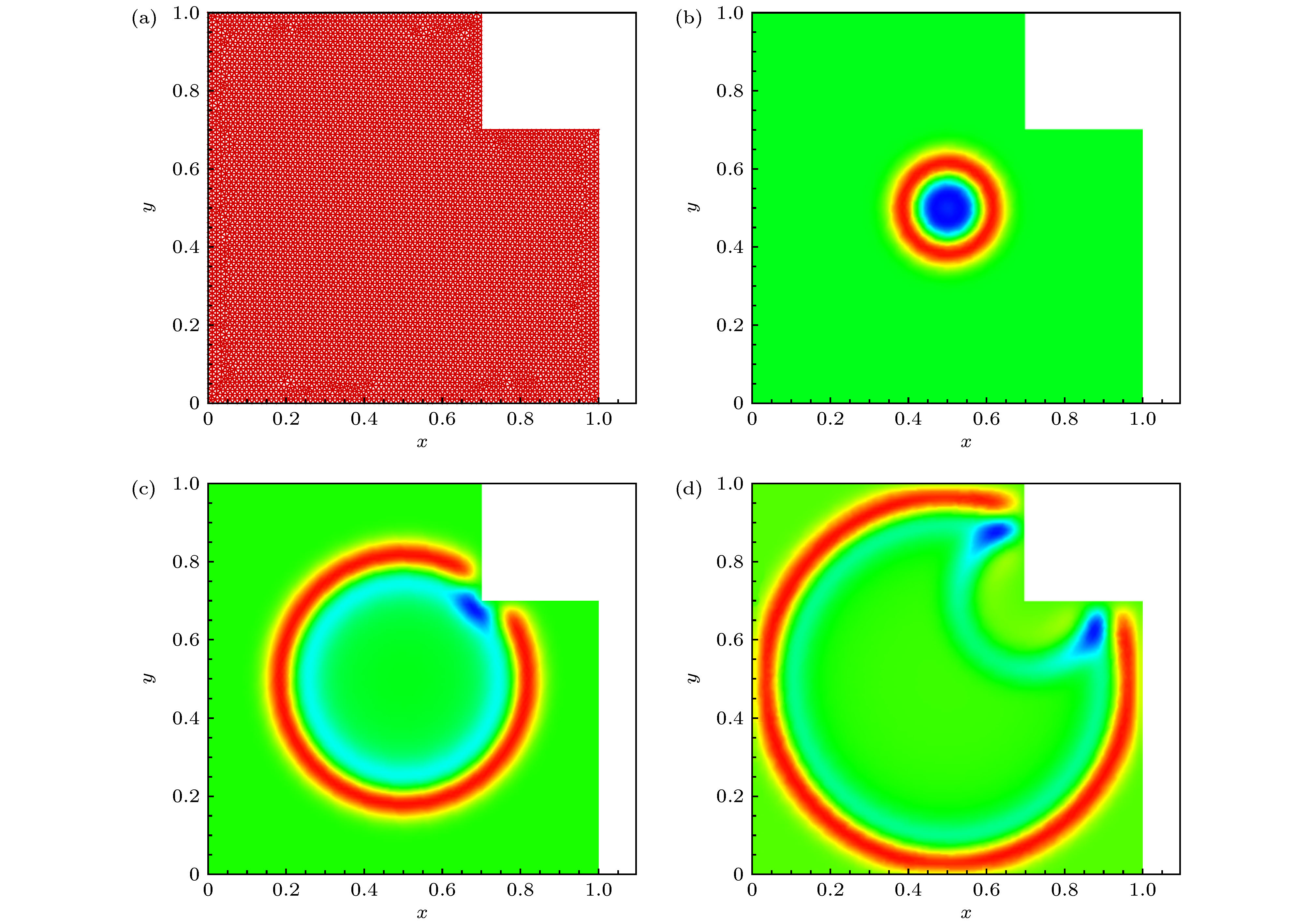
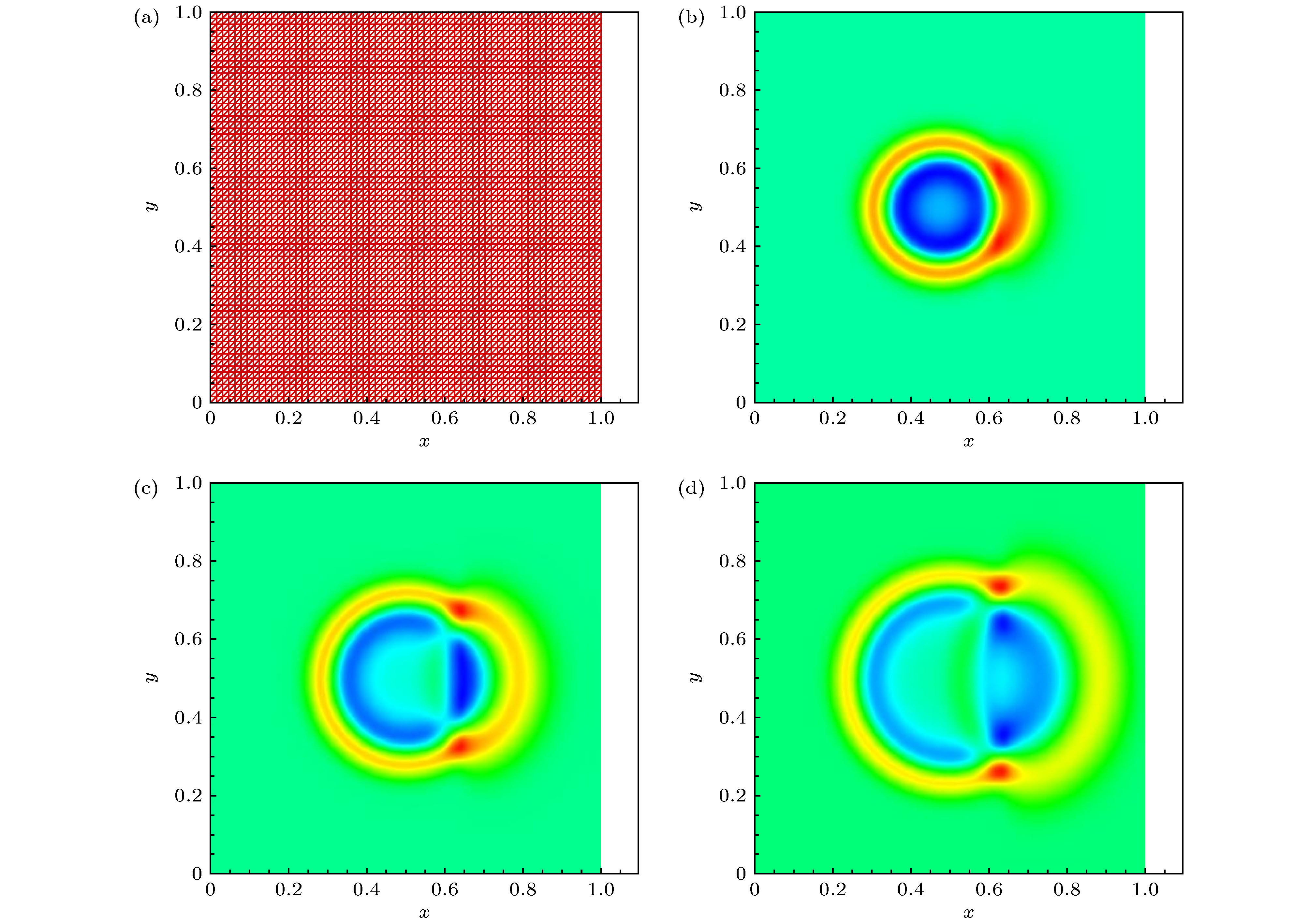
-
波的传播往往在复杂的地质结构中进行, 如何有效地求解非均匀介质中的波动方程一直是研究的热点. 本文将局部间断Galekin(local discontinuous Galerkin, LDG)方法引入到数值求解波动方程中. 首先引入辅助变量, 将二阶波动方程写成一阶偏微分方程组, 然后对相应的线性化波动方程和伴随方程构造间断Galerkin格式; 为了保证离散格式满足能量守恒, 在单元边界上选取广义交替数值通量, 理论证明该方法满足能量守恒性. 在时间离散上, 采用指数积分因子方法, 为了提高计算效率, 应用Krylov子空间方法近似指数矩阵与向量的乘积. 数值实验中给出了带有精确解的算例, 验证了LDG方法的数值精度和能量守恒性; 此外, 也考虑了非均匀介质和复杂计算区域的计算, 结果表明LDG方法适合模拟具有复杂结构和多尺度结构介质中的传播.
-
关键词:
- 波动方程 /
- 广义交替数值通量 /
- 局部间断Galerkin方法 /
- 能量守恒
The wave propagation is often carried out in complex geological structures. Solving the wave propagation problem effectively in inhomogeneous medium is of great interest and has many applications in physics and engineering. In this paper, the local discontinuous Galekin (LDG) method is applied to the numerical solution of the second-order wave equation. Firstly, the auxiliary variables are introduced, and the second-order wave equations are written as a system of first-order partial differential equations. Then the discontinuous Galerkin format is applied to the corresponding linearized wave equations and adjoint equations. We consider the triangulation in this paper. In order to ensure that the discrete format satisfies the energy conservation, the generalized alternating flux is chosen on the element boundary. We proves that the LDG method satisfies the energy conservation. The exponential integral factor method is used in time discretization. In order to improve the computational efficiency, the Krylov subspace method is used to approximate the product of the exponential matrix and the vector. Numerical examples with exact solutions are given in numerical experiments. The numerical results verify the numerical precision and energy conservation of the LDG method. In addition, the calculation of inhomogeneous medium and complex computational regions are considered. The results show that the LDG method is suitable for simulation of complex structures and propagation in multi-scale structured medium.-
Keywords:
- wave equation /
- generalized alternating /
- local discontinuous Galerkin method /
- energy conservation
[1] 周聪, 王庆良 2015 物理学报 64 239101
Google Scholar
Zhou C, Wang Q L 2015 Acta Phys. Sin. 64 239101
Google Scholar
[2] 王飞, 魏兵, 李林茜 2014 物理学报 63 104101
Google Scholar
Wang F, Wei B, Li L X 2014 Acta Phys. Sin. 63 104101
Google Scholar
[3] 王婷, 崔志文, 刘金霞, 王克协 2018 物理学报 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[4] Kampanis N A, Ekaterinaris J, Dougalis V 2008 Effective Computational Methods for Wave Propagation (Virginia beach: Chapman & Hall/CRC) pp135−164
[5] Sjögreen B, Anders P N 2011 J. Sci. Comput. 52 17
[6] Appelö D, Petersson N A 2009 Commun. Comput. Phys. 5 84
[7] 王同科 2010 数值计算和计算机应用 31 64
Wang T K 2010 J. Numerical Methods & Computer Applications 31 64
[8] Safjan A, Oden J 1993 Comput. Methods Appl. Mech. Eng. 103 187
Google Scholar
[9] Cockburn B, Shu C W 1997 SIAM J. Numer. Anal. 35 2440
[10] 赵国忠, 蔚喜军 2012 物理学报 61 110208
Google Scholar
Zhao G Z, Yu X J 2012 Acta Phys. Sin. 61 110208
Google Scholar
[11] Chung E, Engquist B 2009 SIAM J. Numer. Anal. 47 3820
Google Scholar
[12] Chou C S, Shu C W, Xing Y 2014 J. Comput. Phys. 272 88
Google Scholar
[13] Nie Q, Zhang Y T, Zhao R 2006 J. Comput. Phys. 214 521
Google Scholar
[14] 张荣培, 王震, 王语, 韩子健 2018 物理学报 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[15] Wang Y, Zhang R P, Wang Z J, Han Z 2019 Chin. Phys. B 28 50503
Google Scholar
[16] Chen S, Zhang Y 2011 J. Comput. Phys. 230 4336
Google Scholar
-
图 1 (a)算例2的网格剖分和数值解
${w_h}$ 在不同时刻(b)$t = 0.2$ , (c)$t = 0.{\rm{3}}$ , (d)$t = 0.{\rm{4}}$ 时的波传播Fig. 1. (a) The triangulation mesh of Example 2; contour plot of solution
${w_h}$ at different time: (b)$t = 0.2$ ; (c)$t = 0.{\rm{3}}$ ; (d)$t = 0.{\rm{4}}$ .
图 3 (a)算例3的网格剖分和数值解
${w_h}$ 在不同时刻 (b)$t = 0.{\rm{1}}$ , (c)$t = 0.{\rm{3}}$ , (d)$t = 0.{\rm{45}}$ 时的波传播Fig. 3. (a) The triangulation mesh of Example 3; contour plot of solution
${w_h}$ at different time: (b)$t = 0.{\rm{1}}$ ; (c)$t = 0.{\rm{3}}$ ; (d)$t = 0.{\rm{45}}$ .表 1 数值解
${w_h}$ 和p的误差和收敛阶数Table 1. Error and convergence order of numerical solution
${w_h}$ and p.网格数 w的误差 p的误差 ${L^2}$范数下误差 收敛阶 ${L^2}$范数下误差 收敛阶 $8 \times 8$ 2.80 × 10–2 — 6.63× 10–2 — $16 \times 16$ 5.75 × 10–3 2.28 3.40× 10–2 0.96 $32 \times 32$ 1.64 × 10–3 1.81 1.70× 10–2 1.00 $64 \times 64$ 4.62 × 10–4 1.83 8.56× 10–3 0.99 $128 \times 128$ 9.20 × 10–5 2.32 4.30 × 10–3 0.99 
下载: 导出CSV
-
[1] 周聪, 王庆良 2015 物理学报 64 239101
Google Scholar
Zhou C, Wang Q L 2015 Acta Phys. Sin. 64 239101
Google Scholar
[2] 王飞, 魏兵, 李林茜 2014 物理学报 63 104101
Google Scholar
Wang F, Wei B, Li L X 2014 Acta Phys. Sin. 63 104101
Google Scholar
[3] 王婷, 崔志文, 刘金霞, 王克协 2018 物理学报 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[4] Kampanis N A, Ekaterinaris J, Dougalis V 2008 Effective Computational Methods for Wave Propagation (Virginia beach: Chapman & Hall/CRC) pp135−164
[5] Sjögreen B, Anders P N 2011 J. Sci. Comput. 52 17
[6] Appelö D, Petersson N A 2009 Commun. Comput. Phys. 5 84
[7] 王同科 2010 数值计算和计算机应用 31 64
Wang T K 2010 J. Numerical Methods & Computer Applications 31 64
[8] Safjan A, Oden J 1993 Comput. Methods Appl. Mech. Eng. 103 187
Google Scholar
[9] Cockburn B, Shu C W 1997 SIAM J. Numer. Anal. 35 2440
[10] 赵国忠, 蔚喜军 2012 物理学报 61 110208
Google Scholar
Zhao G Z, Yu X J 2012 Acta Phys. Sin. 61 110208
Google Scholar
[11] Chung E, Engquist B 2009 SIAM J. Numer. Anal. 47 3820
Google Scholar
[12] Chou C S, Shu C W, Xing Y 2014 J. Comput. Phys. 272 88
Google Scholar
[13] Nie Q, Zhang Y T, Zhao R 2006 J. Comput. Phys. 214 521
Google Scholar
[14] 张荣培, 王震, 王语, 韩子健 2018 物理学报 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[15] Wang Y, Zhang R P, Wang Z J, Han Z 2019 Chin. Phys. B 28 50503
Google Scholar
[16] Chen S, Zhang Y 2011 J. Comput. Phys. 230 4336
Google Scholar
下载:
计量
- 文章访问数: 7324
- PDF下载量: 81
- 被引次数: 0
