下载:
-
一般来讲, Boussinesq方程可写为
$ u_{tt}+\alpha u_{xx}+\beta (u^2)_{xx}+\gamma u_{xxxx} = 0, $ 其中, 下角标x和t表示偏微分. Boussinesq方程可以用于描绘浅水波、等离子体、非线性晶格等众多物理现象[1-5].
由于该方程应用广泛, 一些特殊形式的或者修正的Boussinesq方程被推导出来研究. 例如, “坏”Boussinesq方程(也叫不适定Boussinesq方程)的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}- u_{xxxx} = 0. $ 这个方程是在1872年由Boussinesq[1]提出来用于描绘浅水波问题的. Benny和Luke[6]发现这个Boussinesq方程非线性弱散色现象的一般近似. “好”Boussinesq方程的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}+ u_{xxxx} = 0. $ 这个方程是作为描绘弦的非线性振动模型提出来的, 也可以用于描绘非线性介质材料中的电磁波[7]. 一种修正的Boussinesq方程的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}- u_{xxtt} = 0. $ 这个方程也经常被称为“改进的”Boussinesq方程[8], 它由流体力学推导而来, 也可以用于描绘波在磁场中的传播, 并取代“坏”Boussinesq方程.
很多不同形式的Boussinesq方程, 是方程(1)的特殊形式. 本文旨在研究Boussinesq方程(1)的可积性、对称性和严格解. 在下文中, 如果没有特殊说明, Boussinesq方程指的是方程(1). 论文结构如下: 在第2节中, 从一个简化的Boussinesq方程的Lax对, 推导出Boussinesq方程(1)的一组Lax对; 在第3节, 对Boussinesq方程(1)进行截断的Painlevé展开, 得到Boussinesq方程的Bäcklund变换; 第4节研究了Boussinesq方程的单参数群变换; 第5节讨论了Boussinesq方程的全点李对称性相似解; 第6节应用CRE (consistent Riccati expansion, CRE)方法证明了Boussinesq方程的CRE相容性. Boussinesq方程孤立波-周期波在第7节进行了讨论; 第8节是本文的结论和讨论.
-
当
$ \alpha = 0 $ ,$ \beta = 1 $ ,$ \gamma = {1}/{3} $ 时, 方程(1)退化成$ v_{\tau\tau}+ (v^2)_{\chi\chi}+\frac{1}{3}v_{\chi\chi\chi\chi} = 0, $ 为了将方程(1)和方程(5)的变量进行区分, 我们将方程(1)中的变量
$ \{u, x, t\} $ 对应地写成方程(5)中的$ \{v, \chi, \tau\} $ . Weiss[9]通过研究方程(5)的painlevé性质, 推出了方程(5)的一组Lax对, 其形式如下$ \psi_{\chi\chi\chi} = -\frac{3}{2} v\psi_\chi-\frac{3}{4}\psi v_{\chi}-\frac{3}{4}\psi{\int v_{\tau}\, {\rm d }\chi}+\lambda \psi \tag{6a},$ $ \psi_{\tau} = \psi_{\chi\chi}+v \psi \tag{6b}.$ $ \begin{split} & u(x,{\mkern 1mu} t) = {\left( {\frac{{3 \gamma }}{{{\beta ^2}}}} \right)^{\frac{1}{3}}}v\left( {\chi ,\tau } \right) - \frac{\alpha }{{2 \beta }},\\ &\chi = \pm \frac{{{\beta ^{\left( {\frac{1}{6}} \right)}} {3^{\left( {\frac{2}{3}} \right)}} x}}{{3 {\gamma ^{\frac{1}{3}}}}},\\ & \tau = \pm \frac{{{3^{\left( {\frac{5}{6}} \right)}} {\beta ^{\left( {\frac{1}{3}} \right)}} t}}{{3 {\gamma ^{\left( {\frac{1}{6}} \right)}}}}.\end{split}$ 结合方程(5)的Lax对(6)式以及标度变换, 可以得到方程(1)的Lax对.
定理1 (Lax对定理)
Boussinesq方程(1)具有如下形式Lax对:
$\begin{split} \phi_{xxx} =\, & - { \frac { \sqrt{3\, \gamma } \beta\phi }{12\,\gamma ^{2}}} \, { \int } u_t\, {\rm d} x \! - { \frac { (2\,u\,\beta + \alpha ) }{4\,\gamma }} \phi_x \\ & - { \frac {\phi \,\beta \,}{ 4\,\gamma }} u_x \pm { \frac { \,\phi \,\lambda \,\sqrt{\beta }}{3\,\gamma }},\end{split} \tag{8a} $ $ \phi_t = \sqrt{3\,\gamma} \phi_{xx} + { \frac {\sqrt{3} \,\phi \,(2\,\beta \,u + \alpha )\,}{6\,\sqrt{ \gamma }}},\tag{8b} $ 这里的λ代表谱函数, φ表示
$ \{x, t\} $ 的任意函数. -
截断Painlevé展开法, 是分析非线性系统最有效的方法之一[10-12]. 对Boussinesq方程(1), 可将u展开成
$ u = u_0+\frac{u_1}{f}+\frac{u_2}{f^2}, $ 这里的
$ u_0, u_1, u_2 $ 和f都是$ \{x, t\} $ 的函数, f是奇异流函数. 将(9)式代入到方程(1)中, 所得到的多项式中, f的所有不同阶次的系数都应该为零. 由$ f^{-6} $ 的系数为零, 可得到$ {u_2} = - { \frac {6\,\gamma \, {f_{x}}^{2}}{\beta }}. $ 由
$ f^{-5} $ 的系数为零, 可得$ {u_1} = { \frac {6\,\gamma \,{f _{{xx}}}}{\beta }}. $ 由
$ f^{-4} $ 的系数, 容易得到$ {u_0} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}\ . $ 将(10)式–(12)式代入到
$ f^{-3} $ 的系数中, 得$ \gamma \left( { \frac {{f_{{xxx}}}}{{f_{x} }}} - { \frac {3}{2}} \,{ \frac {{f_{ {xx}}}^{2}}{{f_{x}}^{2}}} \right)_x + \left({ \frac {{f_{t}}}{ {f_{x}}}} \right)_t + { \frac {{f_{t}}\,}{{f _{x}}}} \left({ \frac {{f_{t}}}{{f_{x}}}} \right)_x = 0, $ 方程(13)在Möbious变换下, 保持形式不变, 因此被称为Schwarzian形式的Boussinesq方程[9].
将(9)式—(13)式代到方程(1)中, 比较所得方程中
$ f^0 $ 的系数, 可发现$ u_0 $ 也是Boussinesq方程的一个解, 这表示$ u = u_0 $ 是Boussinesq方程的一个自Bäcklund变换. 而且, 对以上截断Painlevé展开进行总结, 可得到一个非自Bäcklund变换.定理2 (Bäcklund变换定理)
如果f是Schwarzian形式的Boussinesq方程(13)的解, 那么
$ u = {u_0} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }} $ 也是Boussinesq方程(1)的解.
定理3 (Bäcklund变换定理)
如果f是Schwarzian形式的Boussinesq方程(13)的解, 那么
$\begin{split} u = \, & u_0+\frac{u_1}{f}+\frac{u_2}{f^2} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}}\\ & - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}+\frac{{ 6\,\gamma \,{f _{{xx}}} }}{f\beta}-\frac{ { 6\,\gamma \, {f_{x}}^{2} }}{\beta f^2}\end{split}$ 也是Boussinesq方程(1)的解.
-
将
$ { \dfrac {6\, \gamma \, {f _{{xx}}}}{\beta }} $ 代入Boussinesq方程(1)的对称决定性方程, 可发现$ { \dfrac {6\, \gamma \, {f _{{xx}}}}{\beta }} $ 是Boussinesq方程(1)的一个非局域对称. 为了将传统的点李对称和非局域对称结合在一起, 我们需要建立一个包含Boussinesq方程、Schwarzian形式的Boussinesq方程以及这两个方程的变换关系式的拓展系统, 其形式如下:$ u_{tt}+\alpha u_{xx}+\beta (u^2)_{xx}+\gamma u_{xxxx} = 0, \tag{16a}$ $ \gamma \left( { \frac {{f_{{xxx}}}}{{f_{x} }}} - { \frac {3}{2}} \,{ \frac {{f_{ {xx}}}^{2}}{{f_{x}}^{2}}} \right)_x + \left({ \frac {{f_{t}}}{ {f_{x}}}} \right)_t + { \frac {{f_{t}}\,}{{f _{x}}}} \left({ \frac {{f_{t}}}{{f_{x}}}} \right)_x = 0, \tag{16b}$ $ u = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}, \tag{16c}$ $ f_x = g, \tag{16d}$ $ f_{xx} = h . \tag{16e}$ Boussinesq方程的对称
$ \sigma^u $ 也相应地拓展为满足下式的四分量对称$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $ ,$ \sigma \!=\! \left(\!\!\! \begin{array}{cccc} \sigma^u \\ \sigma^f\\ \sigma^g\\ \sigma^h \end{array}\!\!\!\right) \!=\! \left(\!\!\!\begin{array}{cccc} { \dfrac {6\,\gamma \,{f _{{xx}}}}{\beta }} \\ -f^2\\ -2ff_x\\ -2{f_x}^2-2ff_{xx} \end{array}\!\!\!\right) \!=\! \left(\!\!\!\begin{array}{cccc} { \dfrac {6\,\gamma \,h}{\beta }} \\ -f^2\\ -2fg\\ -2g^2-2fh \end{array}\!\!\right)\ . $ 对方程(16), 我们也可以研究它的全点李对称. 基于这个目的, 四分量对称
$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $ 应该满足Boussinesq方程的线性化的非线性系统. 按照点李对称的方法, 经过计算可得总的对称矢量为$ \underline{V} = C_1 \underline{ V_1} +C_2 \underline{V_2}+C_3 \underline{V_3}+C_4\underline{ V_4}+C_5 \underline{V_5}+C_{6} \underline{V_{6}}\,, $ 各个对称矢量为:
$\begin{split} & \underline{V_1} = \frac{x}{2}\partial_x + t\partial_ t-u\partial_u - { \frac {\alpha }{2 \,\beta }} \partial_u -\frac{g}{2}\partial_g-h\,\partial_h, \\ & \underline{ V_2} = \partial_x, \ \ \ \ \underline{V_3} = \partial_t, \\ & \underline{V_4} = -h\partial_u +{ \frac {\beta f^{2}}{6\,\gamma }} \partial_f +{ \frac {g\,\beta \,f}{3\,\gamma }}\partial_g +{ \frac {\beta (f\,h+g^2)}{3\,\gamma }}\partial_h,\qquad \qquad \\ & \underline{V_5} = -f\partial_f-g \partial_g-h \partial_h, \ \ \ \ \ \underline{V_{6}} = -\partial_f . \\[-10pt]\end{split}$ 其中,
$ \underline{V_1} $ ,$ \underline{V_5} $ 表示标度变换,$ \underline{V_2} $ 表示空间平移不变性,$ \underline{V_3} $ 代表时间平移不变性,$ \underline{V_4} $ 与非局域对称关联, 而$ \underline{V_{6}} $ 则表示相平移不变性.由对称矢量(19)式, 可得到六个单参数不变子群:
$g_{\varepsilon}(\underline{V_1}) : \{x,t,u,f,g,h\} \longrightarrow \left\{x\,{\rm e}^{ \frac {\varepsilon }{2} },t\,{\rm e}^{\varepsilon },{\rm e}^{ - \varepsilon }\,u + { \frac { \alpha }{2\,\beta }}({\rm e}^{ - \varepsilon }-1),f,g\,{\rm e}^{ - \frac {\varepsilon }{2} }, h\,{\rm e}^{ - \varepsilon } \right\}, \tag{20a}$ $ g_{\varepsilon}(\underline{V_2}) : \{x,t,u,f,g,h\} \longrightarrow \{x+\varepsilon, \ t, \ u, \ f, \ g, \ h\}, \tag{20b}$ $ g_{\varepsilon}(\underline{V_3}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t+\varepsilon, \ u, \ f, \ g, \ h\}, \tag{20c}$ $ \begin{array}{l} g_{\varepsilon}(\underline{V_4}) : \{x,t,u,f,g,h\} \longrightarrow \left\{ \begin{array}{ll} x,\ t, \ { u- { \dfrac {6\,\gamma \,\varepsilon ^{2}\,\beta \,g^{2}}{(\varepsilon \,\beta \,f - 6\,\gamma )^{2}}} + { \dfrac {6\, \gamma \,\varepsilon \,h}{\varepsilon \,\beta \,f - 6\,\gamma }}} , \ { \dfrac {6\, \gamma \,f}{6\,\gamma-\varepsilon \,\beta \,f }},\\ { { \dfrac { 36\,g\,\gamma ^{2}}{(\varepsilon \,\beta \,f - 6\,\gamma )^{2}}}},\ \ { { \dfrac {36\,\gamma ^{2 }\,( - 2\,g^{2}\,\varepsilon \,\beta + f\,h\,\varepsilon \,\beta - 6\,h\,\gamma )}{(\varepsilon \,\beta \,f - 6\,\gamma )^{3}}}} \end{array} \right\}, \end{array} \tag{20d}$ $ g_{\varepsilon}(\underline{V_5}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t, \ u, \ {\rm e}^{( - \varepsilon )}f, \ {\rm e}^{( - \varepsilon )} g, \ {\rm e}^{( - \varepsilon )}h\}, \tag{20e}$ $ g_{\varepsilon}(\underline{V_6}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t, \ u, \ f- \varepsilon, \ g, \ h\}. \tag{20f} $ 从以上六个单参数不变子群, 可到到下列Bäcklund变换定理.
定理4 (单参数群变换)
如果
$ \{u(x, t), f(x, t), g(x, t), h(x, t)\} $ 是拓展的Boussinesq系统(16)的一组解, 则下列函数也是拓展的Boussinesq系统(16)的一组解,$ \left\{ \begin{array}{ll} { \overline{u}_1 = {\rm e}^{ - \varepsilon }\,u(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon }) + { \dfrac { \alpha }{2\,\beta }}({\rm e}^{ - \varepsilon }-1)}, \qquad { \overline{f}_1 = f(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })}, \\ { \overline{g}_1 = g(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })\,{\rm e}^{ - \frac {\varepsilon }{2} }}, \qquad \qquad \qquad \ \qquad { \overline{h}_1 = h(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })\,{\rm e}^{ - \varepsilon }} \end{array}\right \}, \tag{21a}$ $ \left\{ \overline{u}_2 = u(x-\varepsilon, t), \ \ \ \overline{f}_2 = f(x-\varepsilon, t),\ \ \ \overline{g}_2 = g(x-\varepsilon, t), \ \ \ \overline{h}_2 = h (x-\varepsilon, t)\right\}, \tag{21b}$ $ \{ \overline{u}_3 = u(x, t-\varepsilon), \ \overline{f}_3 = f(x, t-\varepsilon),\ \ \ \ \ \overline{g}_3 = g(x, t-\varepsilon), \ \ \ \overline{h}_3 = h(x, t-\varepsilon) \}, \tag{21c}$ $ \left \{\begin{array}{ll} { \overline{u}_4 = u(x,t)- { \dfrac {6\,\gamma \,\varepsilon ^{2}\,\beta \,g(x,t)^{2}}{(\varepsilon \,\beta \,f(x,t) - 6\,\gamma )^{2}}} + { \dfrac {6\, \gamma \,\varepsilon \,h(x,t)}{\varepsilon \,\beta \,f(x,t) - 6\,\gamma }}}, \ { \overline{f}_4 = { \dfrac {6\, \gamma \,f(x,t)}{6\,\gamma-\varepsilon \,\beta \,f(x,t) }}}, \\ { \overline{g}_4 = { \dfrac { 36 \gamma^{2}g(x,t)\,}{(\varepsilon \beta f(x,t) - 6 \gamma )^{2}}}},\ { \overline{h}_4 = { \dfrac {36 \gamma ^{2 } ( \varepsilon \beta f(x,t) h(x,t) - 2 \varepsilon \beta g(x,t)^{2}- 6 \gamma h(x,t) )}{(\varepsilon \,\beta \,f(x,t) - 6\,\gamma )^{3}}}} \end{array} \!\!\!\right\}, \tag{21d}$ $ \{ \overline{u}_5 = u(x,t), \ \ \ \overline{f}_5 = {\rm e}^{( - \varepsilon )}f (x,t),\ \ \ \overline{g}_5 = {\rm e}^{( - \varepsilon )}\,g(x,t),\ \ \ \overline{h}_5 = {\rm e}^{( - \varepsilon )}h (x,t)\}, \tag{21e}$ $ \{\overline{u}_6 = u(x,t), \ \ \ \overline{f}_6 = f(x,t)- \varepsilon,\ \ \ \ \overline{g}_6 = g(x,t), \qquad \ \ \ \overline{h}_6 = h(x,t) \}. \tag{21f}$ -
对称性理论是求解偏微分方程的一种有效系统的方法[13-19]. 从对称矢量(19)式, 不仅可以得到单参数不变子群和群不变解, 而且可以得到Boussinesq的相似解和约化方程. 将约化方程的严格解和相似解相结合, 则可以得到所研究系统的严格解. 可得到下列四组非平庸情况.
情况1
$ C_1\neq 0, C_4\neq 0 $ .在种情这况, 群不变量可写为
$ \xi = { \frac {{C_{3}} + {C_{1}}\,t}{{C_{1}}\,(2\,{C _{2}} + {C_{1}}\,x)^{2}}}. $ 相似解的形式为
$ \begin{split}u= \,&{ \frac { {U}(\xi )}{(2\,{C_{2}} + {C_{1}}\,x)^{2}}} - { \frac {(4\,{C_{2}} + {C_{1}}\,x)\, \alpha\,{C_{1}}\,x}{2\,\beta( 2\, {C_{2}} + {C_{1}}\,x)^{2} }} \\ & - { \frac {6\,\gamma\,{C_{4}}\, {H}(\xi ) \,{\rm e}^{( - 2\, {F}(\xi )\,{C_{1}})}\, }{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,\delta }}\\ & \times {\rm tanh}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ] \\ & +{ \frac {6\,\beta\,\gamma\,{C_{4}}^{2}\, {G}(\xi )^{2}\,{\rm e} ^{( - 2\, {F}(\xi )\,{C_{1}})} }{\delta ^{2}\,(2\,{C_{2}} + {C_{1}}\,x)^{2}\,}}\\ & \times {\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2}, \end{split}\tag{23a}$ $ f \!=\! { \frac {3\,\gamma\,{C_{5}} }{C_4\,\beta}}-\frac{\delta}{C_4\,\beta} {\rm tanh} \!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} \!+\! {C_{1}}\,x ) \!+\! \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ],\tag{23b}$ $\begin{split} g =\, &{ \frac { {G}(\xi )\,{\rm e}^{( - {F}(\xi ) \,{C_{1}})}}{\,(2\,{C_{2} } + {C_{1}}\,x)}} \\ & \times{\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2},\end{split}\tag{23c}$ $ \begin{split} h = & { \frac { {H}(\xi )\,{\rm e}^{( - 2\, {F}( \xi )\,{C_{1}})}}{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,}} \\ & \times{\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2} \\ &+{ \frac {2\,\beta\,{C_{4}}\, {G}(\xi )^{2}\, \,{\rm e}^{( - 2\, {F}(\xi )\,{C _{1}})}}{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,\delta }} \\ & \times\frac{{\rm sinh}\!\left[{ \dfrac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]}{{\rm cosh}\!\left[{ \dfrac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^3} , \end{split}\tag{23d}$ 其中
$ \delta = \sqrt{6\, \gamma \, \beta \, {C_{4}}\, {C_{6}} + 9\, \gamma ^{2}\, {C_{5}}^{2}} $ , 约化函数$ \{U(\xi), $ $ F(\xi) $ ,$ G(\xi), H(\xi)\} $ 需要满足相应的约化方程. 这种情况的约化方程非常长, 这里省略不写.情况2
$ C_1\neq 0, C_4 = 0 $ .$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $ 包含$ C_4 $ , 而$ C_4 $ 是与非局域对称相关联的, 那么如果令$ C_4 = 0 $ , 则相似解会变得更加简化. 这样, 相似解为:$ u = - { \frac {4\,x\, \alpha \,{C_{1}}\,{C_{2}} + x^{2}\,\alpha \,{C_{1}}^{2} - 2\, {U}(\xi )\,\beta }{2\,\beta \,(2\,{C_{2}} + {C_{1}}\,x)^{2}} }\,, \tag{24a}$ $ f = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - \frac {2\,{C_{5}}}{{C_{1}}}\right)}\, {F}(\xi ) - { \frac {{C_{6}}}{{C_{5}}}}\,,\tag{24b}$ $ g = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - 1 - \frac {2\,{C_{5}}}{{C_{1}}}\right) }\, {G}(\xi )\,, \tag{24c}$ $ h = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - 2 - \frac {2\,{C_{5}}}{{C_{1}}}\right ) }\, {H}(\xi )\, . \tag{24d}$ 与情况一相比, 时间和空间的对称性都没有改变, 因此这种情况的群不变量与情况一相同, 仍为
$ \xi = { \frac {{C_{3}} + {C_{1}}\,t}{{C_{1}}\,(2\,{C _{2}} + {C_{1}}\,x)^{2}}}\ . $ 将(24b)式代入(16d)式和(16e)式, 则变量f和g变成:
$ g = - 2\,(2\,{C_{2}} + {C_{1}}\,x)^{( - 1 - \frac {2\,{C_{5}}}{{C_{1}}})}\,({C_{1}}{F_{\xi }}\,\xi \, + C_{5} {F} ), $ $\begin{split} h =\,& 2\,(2\,{C_{2}} + {C_{1}}\,x)^{( - 2 - \frac {2 \,{C_{5}}}{{C_{1}}})} (2 {C_{1}}^{2} {F_{\xi \xi }} \xi ^{2}+ 3 {C_{1}}^{2} { F_{\xi }}\,\xi \\ & + {C_{1}} {C_{5}}{F} \, + 4\,{C_{1}} {F_{\xi }} {C_{5}} \xi + 2\,{C_{5}}^{2} {F} ),\\[-12pt]\end{split}$ 将(24b)式代到(16c)式, 可以得到用和F表示的u的表达式, 将(24b)代入到(16b)式, 可以得到F满足的约束方程. 由于这两个式子都很长, 此处省略不写.
情况3
$ C_1 = 0, C_2\neq 0, C_4\neq 0 $ .(18)式和(19)式说明空间x和时间t的对称受到
$ C_1 $ 的影响. 当$ C_1 = 0 $ 时, 群不变量ξ将比情况一和情况二的群不变量简单. 此时, 群不变量变为$ \xi = \frac{C_2 t-C_3x}{C_2}, $ 相似解为:
$ u = {U}(\xi)+{ \frac {3\,\gamma\, C_{4} {\rm e} ^{ \frac {\delta \,{F}(\xi) }{ 3\,{C_{2}}\,\gamma } } {H}(\xi) }{\delta \,\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right] }} - { \frac {24\,\beta\,\gamma\,{C_{4}}^{2} {G}(\xi)^{2} }{\delta ^{2} \left[{\rm e}^{ \frac {\delta \, (x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{2}}}, \tag{29a}$ $ f = - { \frac {\delta }{ \beta \,{C_{4}}}} {\rm tanh}\left[ { \frac {\delta \,(x + F (\xi) )}{6\,\gamma\,{C_{2}} }} \right ] + { \frac {3\,\gamma \,{C_{5}}}{ \beta \,{C_{4}}}}, \tag{29b}$ $ g = - { \frac {2\, {G}(\xi) }{ {\rm cosh}\left[{ \dfrac {\delta \,(x + {F}(\xi) )}{3\,{C_{2}}\,\gamma }} \right] + 1} }, \tag{29c}$ $ h = { \frac { {\rm e}^{ \frac {\delta \, (2\,{F}(\xi) +x)}{3\,{C_{2}}\,\gamma } } {H}(\xi) }{\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{2}}} - { \frac {16\,\beta\,{C_{4}}\, G(\xi)^{2}\,{\rm e}^{ \frac {\delta \,(x+F(\xi)) }{3\,{C_{2}}\,\gamma } } }{ \delta \,\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{3}}} .\tag{29d}$ 其中
$ F(\xi) $ 满足$ \begin{split}& 27 {C_{2}}^{2}\,{C_{3}}^{5} \gamma ^{2} {F_{\xi \xi }}^{3} + 4 {F_{\xi \xi }} {C_{3}}^{4}\,{C_{2}} \delta ^{2}\,{F_{ \xi }}^{3}\\ + & ( - 6 {C_{3}}^{3} {C_{2}}^{2} \delta ^{2} {F_{ \xi \xi }} + 9\,{C_{3}}^{5}\,{F_{\xi \xi \xi \xi }}\,{C_{2}}^{2}\,\gamma ^{2})\,{F_{\xi }}^{2}\\ + & \{[ 2\,{C_{2}}^{3}\,( 2\,\delta ^{2}\,{C_{3}}^{2}-9\,\gamma \,{C_{2}}^{4})\\ - & 36\,{C_{2}}^{2}\,{C_{3}}^{5}\,\gamma ^{2}\,{F_{\xi \xi \xi }} ]\,{F_{\xi \xi }} - 18\,{C_{2}}^{3}\,{C_{3 }}^{4}\,{F_{\xi \xi \xi \xi }}\,\gamma ^{2}\}\,{F_{\xi }} \\ - & {C_{3}}^{5} {F_{\xi \xi }}\,\delta ^{2}\,{F_{\xi }}^{4} \\ + & \left[36 \gamma ^{2} {C_{3}}^{4} {C_{2}}^{3} {F_{\xi \xi \xi }} + { \frac {{C_{2}}^{4}\,(9\, \gamma {C_{2}}^{4} - \delta ^{2} {C_{3}}^{2})}{{C_{3}}}}\right] \\ \times & {F _{\xi \xi }} + 9\gamma ^{2} {C_{2}}^{4} {F_{\xi \xi \xi \xi }} {C _{3}}^{3} = 0 . \\[-10pt] \end{split} $ 将(29b)式代到(16c)式, 可得到关于Boussinesq方程的下列Bäcklund变换.
定理5 (Bäcklund变换定理).
如果F满足(30)式, 则Boussinesq方程的解为
$ \begin{split} u =& - { \frac {1}{6}} \, { \frac {({C_{2}} - {F_{\xi }}\,{C_{3}})^{2}\,\delta ^{2}\,}{\beta \,\gamma \,{C_{2}}^{4}}}{\rm tanh}\left[ { \frac {\delta \,(x + {F} )}{6\,{C_{2}}\, \gamma }}\right ]^{2} \\ &+ { \frac {\delta \,{C_{3}}^{2}\,{F_{\xi \xi }} }{{C _{2}}^{3}\,\beta }} {\rm tanh}\left[ { \frac {\delta \,(x + {F} )}{6\,{C_{2}}\, \gamma }}\right ] \\ &- \frac {1}{18 \gamma \beta{C_{2}}^{4}({C_{2}} - {F _{\xi }}\,{C_{3}})^{2} } \{ 3\,{C_{2}}^{2}\,(3\,\gamma \,{C_{2}}^{4} \\ & + 3\,{C_{2}}^{2} \,\alpha \,\gamma \,{C_{3}}^{2} - 4\,\delta ^{2}\,{C_{3}}^{2})\,{ F_{\xi }}^{2}\\ & + [36\,{F_{\xi \xi \xi }}\,{C_{3}}^{4}\,{C_{2}}^{ 2}\,\gamma ^{2} - 2\,{C_{2}}^{3}\,{C_{3}}\,(9\,{C_{2}}^{2}\, \alpha \,\gamma\\ &- 4\,\delta ^{2})]\,{F_{\xi }} - 27\gamma ^{2} {F_{\xi \xi }}^{2}\,{C_{3}}^{4}\,{C_{2}}^{2} \\ &- 2 \delta ^{2} {F_{\xi }}^{4} {C_{3}}^{4} - 36 {F_{\xi \xi \xi }} {C_{3}}^{3} {C_{2}}^{3 }\,\gamma ^{2} \\ &+ {C_{2}}^{4}\,(9\alpha \gamma {C_{2}}^{2} - 2 \delta ^2)+ 8\,\delta ^{2}\,{C_{2}}\,{F_{\xi }}^{3}\,{C_{3}} ^{3} \}. \end{split}$ 情况4
$ C_1 = 0, C_2\neq 0, C_4 = 0 $ .这种情况下, 拓展系统(16)的相似解为:
$ u = {U} (\xi ), \tag{32a} $ $ f = {\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}\, {F}(\xi ) - { \frac {{C_{6}}}{{C_{5}}}}, \tag{32b}$ $ g = G(\xi )\,{\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}, \tag{32c}$ $ h = {H}(\xi )\,{\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}, \tag{32d}$ 这里, 群不变量ξ为
$ \xi = \frac{C_2 t-C_3x}{C_2}. $ 将(32b)式代入到(16b)式, 可得到
$ F(\xi) $ 满足的约束方程. 将(32b)式代入到(16c)式, 则得到下列定理.定理6 (Bäcklund变换定理).
如果
$ F(\xi) $ 满足(32b)式, 则Boussinesq方程的解可以写为$ \begin{split} u = & - { \frac {1}{2}}\frac{1}{({F_{\xi }} { C_{3}} + {F} {C_{5}})^{2} {C_{2}}^{2} \beta} \left\{ [4\,\gamma {F_{\xi \xi \xi }}\,{C_{3}}^{4}\right. \\ &+ 2\,{C_{3}} {C_{5}} {F} (2\,{C_{5}}^{2}\,\gamma + \alpha \,{C_{2}}^{2})] {F_{\xi }} - 3\,\gamma \,{F_{\xi \xi }}^{2}\,{C_{3}}^{4} \\ & +{C_{2}}^{2} (\alpha \,{C_{3}}^{ 2} + {C_{2}}^{2}) {F_{\xi }}^{2} + 6\, \gamma \,{F}{F_{\xi \xi }}\,{C_{3}}^{2}{C_{5 }}^{2}\,\\ & \left.+ 4\,\gamma \,{F_{\xi \xi \xi }} {C_{3}}^{3} {F} {C_{5}} + {C_{5}}^{2} {F} ^{2} ({C_{5}}^{2}\,\gamma + \alpha {C_{2}}^{2})\right\} . \end{split} $ -
本节将通过CRE (consistent Riccati expansion, CRE)方法来讨论Boussinesq方程的严格解[20]. Riccati方程的形式为
$ R_w = a_0+a_1R(w)+a_2 R(w)^2, $ 这里的
$ a_0 $ ,$ a_1 $ 和$ a_2 $ 是任意常数. Riccati方程的严格解可写为$ R(w) = -\frac{\sqrt{\theta}}{2\, a_2}\tanh \left(\frac{\sqrt{\theta}\, w}{2}\right)+\frac{ a_1}{2\, a_2}, $ 其中,
$ \theta\equiv {a_1}^2-4a_0\, a_2. $ 对于一个偏微分系统
$ \begin{split} & P(x, t, v) = 0,\ \ \ P = \{P_1, P_2,..., P_m\}, \\ & x = \{x_1, x_2,..., x_n\}, \ \ \ v = \{v_1, v_2,..., v_m\}, \end{split} $ 我们可假设它可以展开为
$ v_i = \sum\limits_{j = 0}^{J_i} v_{i,j}R^j(w), $ 这里的
$ R(w) $ 是Riccati方程的严格解. 将(39)式代入到(38)式, 并令$ R^i(w) $ 的系数为零, 可得:$ P_{j,i}(x,t,v_{l,k},w) = 0. $ 如果系统(40)是自洽的, 则展开式(39)式是“CRE”, 且非线性系统(38)是“CRE”相容系统[20].
为了得到孤立波-周期波碰撞解, 可应用CRE方法. CRE方法可被用于证明一个系统是CRE相容系统, 并可用于寻求非线性系统的碰撞波解. 对Boussinesq方程, u可展开成截断展开的形式:
$ u = u_3+u_4 R(w)+u_5 {R(w)}^2,$ 这里,
$ u_3, \ u_4, \ u_5 $ 和w都是x和t的函数,$ R(w) $ 是Riccati方程的一个解.将(35)式和(41)式代入到方程(1)中, 并令
$ R(w) $ 所有阶次的系数为零, 可得$\begin{split} {u_{3}} = & -\, { \frac { \gamma \,({a_{1}}^{2} + 8\,{a_{2}}\, {a_0})\,{w_{x}}^{2}}{ 2\, \beta }} - { \frac { \alpha + 6\,\gamma \,{w_{{xx}}}\,{a_{1}}}{2\,\beta }} \\ & - { \frac {2\,\gamma \,{w_{{xxx}}}}{{w_{x}}\, \beta }} - { \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{{xx}}}^{2}}{2\,\beta \,{w_{x}} ^{2}}}, \\[-18pt]\end{split} \tag{42a}$ $ {u_{4}} = - { \frac {6\,{a_{2}}\,\gamma \,({w_{x}}^{2 }\,{a_{1}} + {w_{{xx}}})}{\beta }}, \tag{42b}$ $ {u_{5}} = - { \frac {6\,\gamma \,{w_{x}}^{2}\,{a_{2}} ^{2}}{\beta }},\tag{42c}$ 这里w满足
$\begin{split} {w_{t}}^{2} {w_{ {xx}}}\, & - \gamma (4 {a _{2}} {a_0}\! -\! {a_{1}}^{2}) {w_{ {xx}}} {w_{x}}^{4} \!-\! ( \gamma {w_{ {xxxx}}}\! +\! {w_{ {tt}}}) {w_{x}} ^{2}\\ &+ 4 \gamma {w_{x}} {w_{ {xx}}} {w_{ {xxx}}} - 3 \gamma {w_{ {xx}}}^{3} = 0. \\[-10pt]\end{split} $ 通过CRE和CRE相容性的定义, Boussinesq方程显然是一个CRE相容系统. 基于以上讨论, 可得到如下定理:
定理7 (CRE相容性定理)
Boussinesq方程是一个CRE相容系统. 如果w是相容性条件(43)式的一个解, 则下列形式的u也是Boussinesq方程的一个解.
$ \begin{split} u = & u_3+u_4 R(w)+u_5 {R(w)}^2 \\ = & - \,{ \frac { \gamma \,({a_{1}}^{2} + 8\,{a_{2}}\, {a_0})\,{w_{x}}^{2}}{ 2\,\beta }} - { \frac { \alpha + 6\,\gamma \,{w_{{xx}}}\,{a_{1}}}{2\,\beta }} \\ & - { \frac {2\,\gamma \,{w_{{xxx}}}}{{w_{x}}\, \beta }} - { \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{{xx}}}^{2}}{2\,\beta \,{w_{x}} ^{2}}} \\ & - { \frac {6\,{a_{2}}\,\gamma \,({w_{x}}^{2 }\,{a_{1}} + {w_{{xx}}})}{\beta }} R(w) \\ & - { \frac {6\,\gamma \,{w_{x}}^{2}\,{a_{2}} ^{2}}{\beta }} R(w)^2, \end{split} $ -
从Boussinesq方程的CRE性质, 可进一步研究Boussinesq方程的严格解. 将(36)式代入到(44)式中可得
$ \begin{split} u = & - { \frac {3}{2}} \, { \frac {{w_{x}}^{2}\,\gamma \,\,\theta }{ \beta }} {\rm tanh}\left( { \frac {w\,\sqrt{\theta }}{2}} \right)^{2}\\ & + { \frac {3\,\gamma \,{w_{{xx}}}\, \, \sqrt{\theta }}{\beta }}{\rm tanh}\left({ \frac {w\,\sqrt{\theta }}{2}} \right) - { \frac {\alpha }{2\,\beta }} \\ & - { \frac {\gamma \,(4\,{a _{2}}\,{a_{0}} - {a_{1}}^{2})\,{w_{x}}^{2}}{\beta }} - { \frac {2\,\gamma \,{w_{ {xxx}}}}{{w_{x}}\, \beta }}\\ & - { \frac {1}{2}} \,{ \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{ {xx}}}^{2}}{\beta \,{w_{x}} ^{2}}} . \end{split} $ 从(45)式可看到, 如果我们想知道u的具体形式, 那么需要先知道w的表达式. 如果w具有如下形式:
$ w = {k_{1}}\,x + \omega_1\,t + {a_{3}}\,E_{\pi}( {\rm sn}({k_{2}}\,x + \omega_2\,t, \,m), \,n, \,m), $ 这里
$ k_1, k_2, \omega_1, \omega_2, a_3, n $ 和m是常数,$ E_{\pi} $ 是第三类不完全椭圆积分. 将(46)式代入到(43)式中, 并令$ {\rm sn}({k_{2}}\, x + \omega_2\, t, \, m) $ 的所有不同阶次的系数为零, 可发现参数应该满足:$ \left\{\begin{aligned} & {a_{0}} = { \frac {n\,{ a_{1}}^{2}\,{a_{3}}^{2} - 4\,m^{2} + 4\,m^{2}\,n - 4\,n^{2} + 4\, n}{4\, {a_{3}}^{2}\,{a_{2}}\,n}}, \\ & \gamma = { \frac {3\,[{k_{1}}^{2}\,{a _{4}}\,n^{2} - {k_{1}}\,{a_{4}}^{2}\,(1 + m^{2})\,n + m^{2}\,{a_{ 4}}^{3}]\,{k_{1}}\,{\omega _{2}}^{2}\,n\,{a_{3}}^{2}}{{k_{2}}^{2} \,[{k_{1}}^{2}\,({k_{1}} + 3\,{a_{4}})\,n^{2} - 2\,{k_{1}}\,{a_{4 }}\,({k_{1}} + {a_{4}})\,(1 + m^{2})\,n + m^{2}\,({a_{4}} + 3\,{k _{1}})\,{a_{4}}^{2}]^{2}}},\\ & {\omega _{1}} = - { \frac {{\omega _{ 2}} {k_{1}} [{k_{1}}^{2} (3 {a_{4}} - {k_{1}}) n^{2} - 2 {k _{1}} {a_{4}} (2 {a_{4}} - {k_{1}}) (1 + m^{2}) n + m^{2} ( 5 {a_{4}} - 3 {k_{1}}) {a_{4}}^{2}]}{{k_{2}} [{k_{1}}^{2}\,({ k_{1}} + 3 {a_{4}})\,n^{2} - 2 {k_{1}} {a_{4}} ( {k_{1}} + {a_{4}} ) (1 + m^{2})\,n + m^{2} ({a_{4}} + 3 \,{k_{1}})\,{a_{4}}^{2}]}},\end{aligned} \right. $ 或
$ \left\{\begin{aligned} & {\omega _{1}} = - { \frac {1}{2}} \,{ \frac {{\omega _{2}}\,{k_{1}}}{{k_{2}}}}, \\ & \gamma = - { \frac {3}{16}} \, { \frac {{\omega _{2}}^{2}\,{a_{3}}^{2}\,(3\,{a_{4}} - 2\,{k_{1}}\,n)}{{k_{2}}^{2}\,{a_{4}}\,({k_{1}}\,n - {a_{4}})^{ 2}}}, \\ & m = \pm { \frac { \sqrt{( 2\,{k_{1}}\,n- 3\,{a _{4}})\,{a_{4}}\,{k_{1}}\,n\,({k_{1}}\,n - 2\,{a _{4}})}}{{a_{4}}\,( 3\,{a_{4}}- 2\,{k_{1}}\,n)}},\\ &{a_{0}} = { \frac {1}{4}} \, { \frac {{a_{1}}^{2}}{{a_{2}}}} - { \frac {(n - 1)\,({k_{1}}^{2}\,n + 2\,{k_{1}}\,n\,{a_{3}}\,{k_{2}} - {k_{1}}^{2} - 4\,{k_{1}}\,{a_{3}}\,{k_{2}} - 3\,{a_{3}}^{2}\,{ k_{2}}^{2})}{{a_{2}}\,( 2\,{k_{1}}\,n - 3\,{a_{4}} )\,{a_{3}}^{2}\,{a_{4}}}}, \end{aligned} \right. $ 这里
$ {a_{4}} = {k_{1}} + {a_{3}}\, {k_{2}} $ .$ u = { \frac {3}{2}} \, { \frac {(a_{4}-{k_{1}}\,n\,S^{2} )^{2} \gamma \theta T^{2}}{(n\,S^{2} - 1)^{2} \beta }} + { \frac {6 \gamma {a_{3}} {k_{2}}^{2} n S C {D} \sqrt{\theta }\,T}{(n S^{2} - 1)^{2} \beta }} - \frac{ [ a_5 S^{8} + a_6 S^{6} + a_7 S^{4} +a_8 S^{2} + a_9 ]}{2[({k_{1}} n S^{2} -{a_{4}} )^{2} (n S^{2} - 1)^{2} \beta ]}, $ 其中
$ \begin{split} T\equiv \, &{\rm tanh}\left\{{ \frac {1}{2}} \,\sqrt{\theta }\,\left [{ k_{1}}\,x + {\omega _{1}}\,t + {a_{3}}\,E_{\pi}( {\rm sn}({k_{2}}\,x + \omega_2\,t, \,m), \,n, \,m)\right ]\right\}, \\ S\equiv\, &{\rm sn}({k_{2}}\,x + \omega_2\,t, \,m),\ C\equiv{\rm cn}({k_{2}}\,x + \omega_2\,t, \,m), \ D\equiv{\rm dn}({k_{2}}\,x + \omega_2\,t, \,m), \\ a_5 = \, & - n^{3} (2 n \gamma \theta {k_{1}}^{4} - \alpha {k_{1}}^{2} n - {\omega _{1}}^{2} n + 8 \gamma {a_{3}} {k_{2}}^{3} {k_{ 1}} m^{2}), \\ a_6 =\, & 2 n^3[ 8 \gamma a_{3}{k_2}^{3}k_{1} ( m^2 + 1)+ 4 \gamma {a_{4}} \theta {k_{1}}^{3}- \alpha {k_{1}}^{2} - \alpha {k_{1}} {a_{4}} - 2 {\omega _{1}}^{2} - \omega _{1} {a_{3}} \omega _2] - 4 n^{2}m^{2} {a_{3}}\gamma {k_{2}}^{3}( a_4 +3 {k_{1}} ), \\ a_7 = \, & 24 n\gamma {a_{3}}{k_{2}}^{3}( {a_{4}}\,m^{2} - n^2 {k_{1}}) + n^2( {\omega _{ 2}}^{2} {a_{3}}^{2} - 4\,\gamma \,{a_{3}}^{2} {k_{2}}^{4} - 12 \gamma {k_{1}}^{2} {a_{4}}^{2} {a_{1}}^{2} \\ & + 6 {\omega _{1}}^{2} + 48 \gamma {a_{2} } {k_{1}}^{2} {a_{4}}^{2} {a_{0}} + 6\,{\omega _{1}} {a_{3 }} {\omega _{2}} - 4 \gamma {a_{3}}^{2} {k_{2}}^{4} m^{2} + 6 \alpha {k_{1}} {a_{4}} + \alpha {a_{3}}^{2} {k_{2}}^{2} ), \\ a_8 =\, & 4 \gamma n^2 {a_{3}} {k_{2}}^{3} ({k_{1}}+3 {a_{4}}) +8n \gamma{k_{1}} {a_{4}}^{3} \theta - 16\,n\gamma {a_{3}} {k _{2}}^{3}a_{4}( m^{2} + 1) \\ & -2n( {a_{3}}^{2} {\omega _{2}}^{2} + \alpha {k_{1}} {a_{4}} + 2 {\omega _{1}}^{2} + 3 { \omega _{1}} {a_{3}} {\omega _{2}} + {a_{4}}^{2} \alpha), \\ a_9 = & {a_{4}}^{2} \alpha +( {a_{3}} {\omega _{2}} + {\omega _{1}})^{2} + 8 {a_{3}} \gamma {k_{2}}^{3} n {a_{4}} - 2 \gamma {a_{4}} ^{4} \theta, \end{split} $ 图1和图展示了满足约束关系(47)的解(49)式. 图1中的自由参数选为{n = 0.2, m = 0.5, a1 = 1, a3 = 1, k1 = 1, k2 = 1,
$ \omega_2 = 1, \alpha = -0.8, \beta = 1 \} $ , 图2中的自由参数选为{n = 0.2, m = 0.9, a1 = 1, a3 = 1, k1 = 1, k2 = 1,$\omega_2 = 1, \alpha = -0.8, \beta = 1 \} $ . 图1和图2展示了亮孤子和周期波的碰撞行为. 图3展示了图1和图2中u的密度函数, 图3(a)对应图1, 图3(b)对应图2. 两种情况的周期波和孤立波的方向是一致的, 而碰撞处的形状则不相同.
图4和图5展示了满足参数限制(48)式的碰撞波解(49)式, 里边的周期波在扭结孤立波上运动, 而不是在常数背景上运动. 图4中的自由参数选为 {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22,
$\omega_2 = 1, \alpha = -400, \beta = 80 \} $ , 其中(48)式中的m选“+”; 图5中的自由参数选为{n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1,$ \alpha = -14,\; \beta = 6 \} $ , 其中(48)式中的m选“–”. 图6展示了图4和图5中u的密度函数, 图6(a)对应图4, 图6(b)对应图5. 图6清楚地展示了扭结孤立波和周期波的碰撞.
图 4 参数关系满足(48)式的碰撞波解(49)式的演化图. 自由参数为 {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}
Figure 4. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are chosen as {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}.
图 5 参数关系满足(48)式的碰撞波解(49)式. 自由参数为{n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}
Figure 5. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are selected as {n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}.
-
本文推导了Boussinesq方程的Lax对, 说明Boussinesq方程是Lax可积模型. 运用截断Painlevé展开法研究了Boussinesq方程, 得到了Boussinesq方程的自Bäcklund变换, 以及Boussinesq方程和Schwarzian形式的Boussinesq方程之间的非自Bäcklund变换. 研究了Boussinesq方程的全点李对称, 得到了单参数群变换和单参数子群不变解. 运用CRE方法研究了Boussinesq方程, 证明了Boussinesq方程是一个CRE相容模型, 得到了Boussinesq方程的孤立波-椭圆余弦波碰撞解. Boussinesq方程广泛地应用于描绘流体动力学、电磁学、等离子体、非线性晶格等物理现象. 它作为一个著名的孤立子方程, 各种各样的激发模式, 以及它在各种物理情景中的应用, 值得不断深入研究.
感谢楼森岳教授和任博博士的宝贵讨论.
-
Boussinesq方程是流体力学等领域一个非常重要的方程. 本文推导了Boussinesq方程的Lax对. 借助于截断Painlevé展开, 得到了Boussinesq方程的自Bäcklund变换, 以及Boussinesq方程和Schwarzian形式的Boussinesq方程之间的Bäcklund变换. 探讨了Boussinesq方程的非局域对称, 研究了Boussinesq方程的单参数群变换和单参数子群不变解. 运用Riccati展开法研究了Boussinesq方程, 证明Boussinesq方程具有Riccati展开相容性, 得到了Boussinesq方程的孤立波-椭圆余弦波解.
-
关键词:
- Boussinesq方程 /
- lax对 /
- Bäcklund变换 /
- Riccati展开
The Boussinesq equation is a very important equation in fluid mechanics and some other disciplines. A Lax pair of the Boussinesq equation is proposed. With the help of the truncated Painlevé expansion, auto-Bäcklund transformation of the Boussinesq equation and Bäcklund transformation between the Boussinesq equation and the Schwarzian Boussinesq equation are demonstrated. Nonlocal symmetries of the Boussinesq equation are discussed. One-parameter subgroup invariant solutions and one-parameter group transformations are obtained. The consistent Riccati expansion solvability of the Boussinesq equation is proved and some interaction structures between soliton-cnoidal waves are obtained by consistent Riccati expansion.[1] Boussinesq J 1872 J. Math. Pures Appl. 17 55
[2] Ursell F 1953 Proc. Cambridge Philos. Soc. 49 685
Google Scholar
[3] Daripa P 1998 J. Comput. Appl. Math. 100 161
Google Scholar
[4] Guo B, Gao Z, Lin J 2016 Commun. Theor. Phys. 64 589
[5] Liu W 2009 Z. Naturforschung A 64 709
Google Scholar
[6] Benny D J, Luke J C 1964 J. Math. Phys. 43 309
Google Scholar
[7] Himonas A A, Mantzavinos D 2015 J. Differ. Equations 258 3107
Google Scholar
[8] Li S, Zhang W, Bu X 2017 J. Math. Anal. Appl. 449 96
Google Scholar
[9] Weiss J 1983 J. Math. Phys. 24 1405
Google Scholar
[10] Guo B X, Lin J 2013 Int. J. Mod. Phys. B 30 1640013
[11] Guo B X, Gao Z J, Lin J 2016 Commun. Theor. Phys. 66 589
Google Scholar
[12] Liu Y K, Li B 2016 Chin. J. Phys. 54 718
Google Scholar
[13] Gao X N, Lou SY, Tang X Y 2013 J. High Energy Phys. 5 029
[14] Olver P J 1993 Applications of Lie Group to Differential Equations (2nd ed.) (New York: Springer) pp75–238
[15] Liu P, Zeng B Q, Ren B 2015 Commun. Theor. Phys. 63 413
Google Scholar
[16] Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202
Google Scholar
[17] Liu P, Zeng B Q, Deng B B, Yang J R 2015 AIP Adv. 5 087162
Google Scholar
[18] Liu P, Wang Y X, Ren B, Li J H 2016 Commun. Theor. Phys. 66 595
Google Scholar
[19] 焦小玉, 贾曼, 安红利 2019 物理学报 68 140201
Google Scholar
Jiao X Y, Jia M, An H L 2019 Acta Phys. Sin. 68 140201
Google Scholar
[20] Lou S Y 2015 Stud. Appl. Math. 134 372
Google Scholar
-
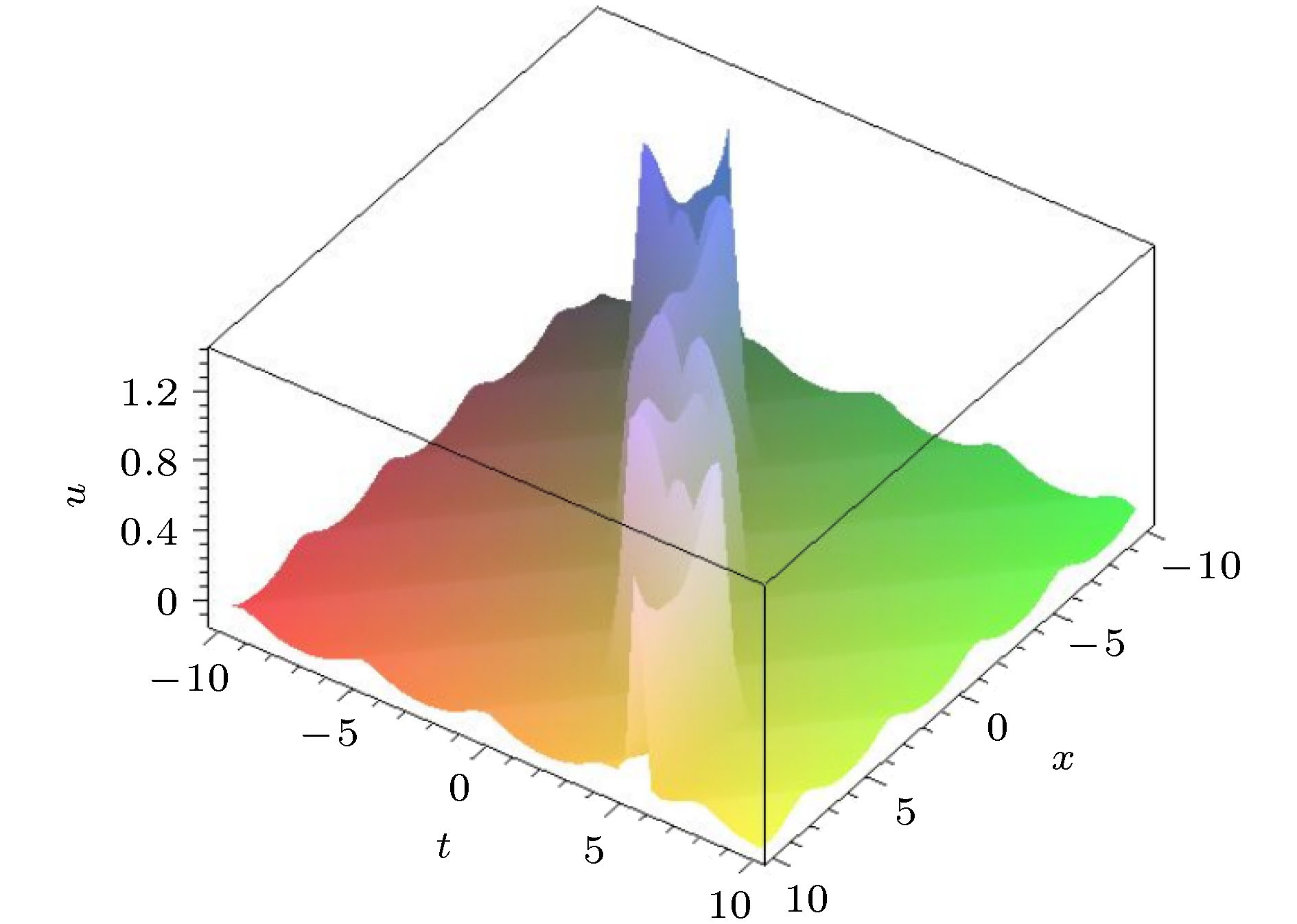
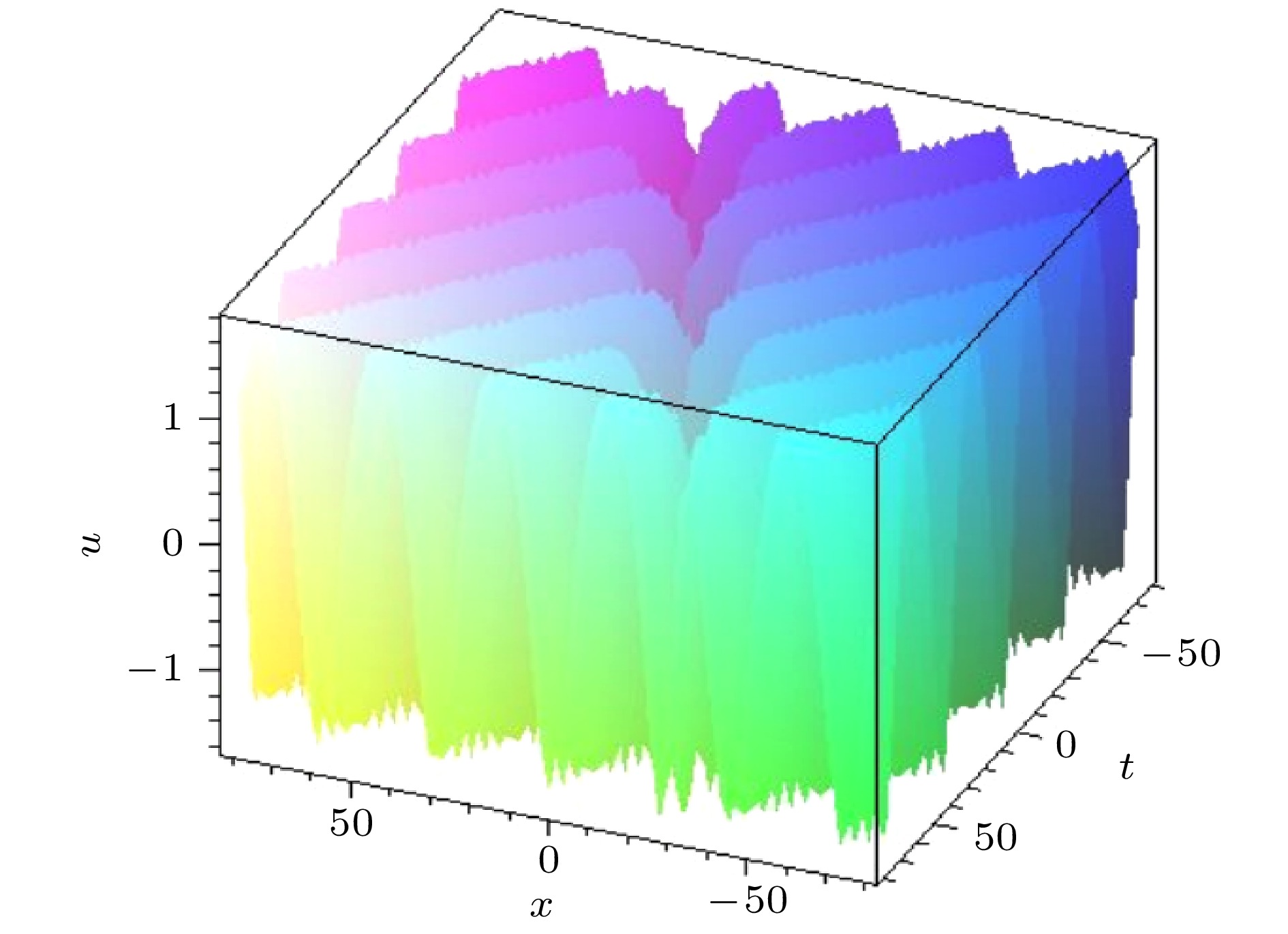
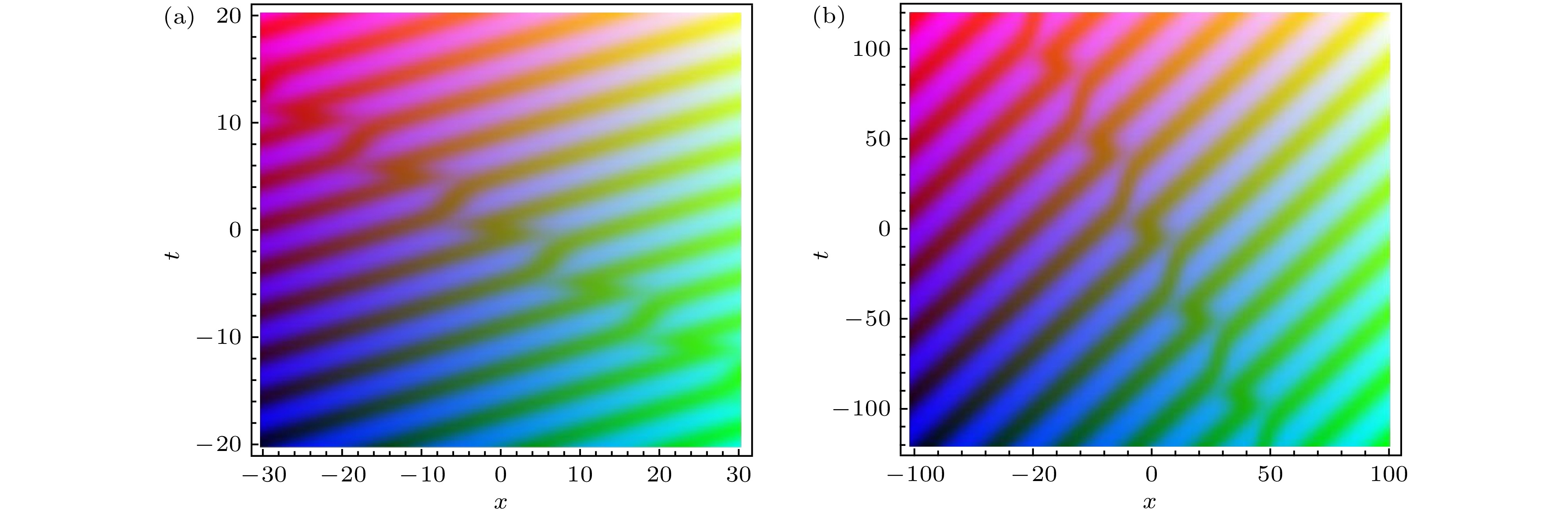
图 4 参数关系满足(48)式的碰撞波解(49)式的演化图. 自由参数为 {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}
Fig. 4. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are chosen as {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}.
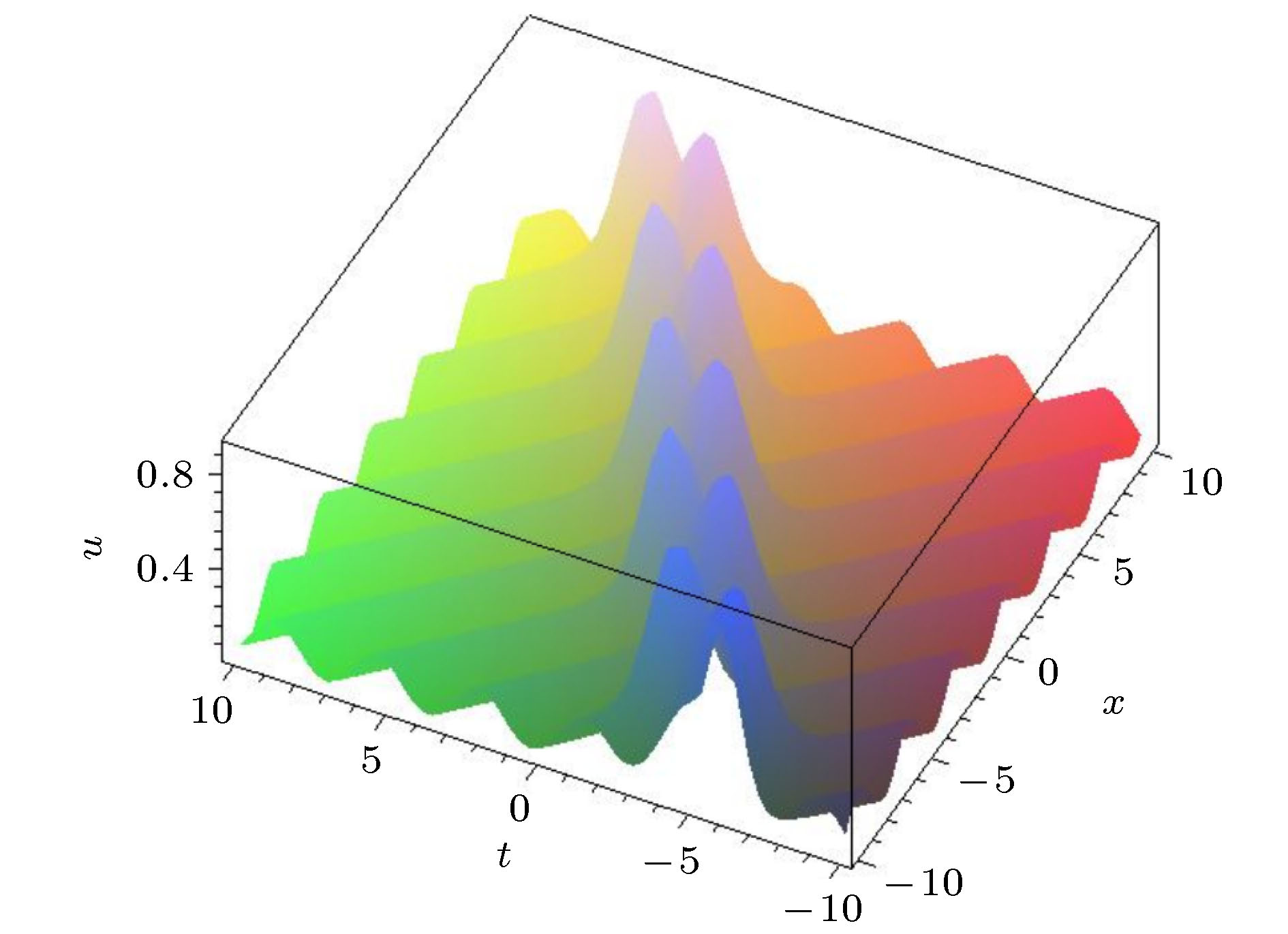
图 5 参数关系满足(48)式的碰撞波解(49)式. 自由参数为{n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}
Fig. 5. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are selected as {n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}.
-
[1] Boussinesq J 1872 J. Math. Pures Appl. 17 55
[2] Ursell F 1953 Proc. Cambridge Philos. Soc. 49 685
Google Scholar
[3] Daripa P 1998 J. Comput. Appl. Math. 100 161
Google Scholar
[4] Guo B, Gao Z, Lin J 2016 Commun. Theor. Phys. 64 589
[5] Liu W 2009 Z. Naturforschung A 64 709
Google Scholar
[6] Benny D J, Luke J C 1964 J. Math. Phys. 43 309
Google Scholar
[7] Himonas A A, Mantzavinos D 2015 J. Differ. Equations 258 3107
Google Scholar
[8] Li S, Zhang W, Bu X 2017 J. Math. Anal. Appl. 449 96
Google Scholar
[9] Weiss J 1983 J. Math. Phys. 24 1405
Google Scholar
[10] Guo B X, Lin J 2013 Int. J. Mod. Phys. B 30 1640013
[11] Guo B X, Gao Z J, Lin J 2016 Commun. Theor. Phys. 66 589
Google Scholar
[12] Liu Y K, Li B 2016 Chin. J. Phys. 54 718
Google Scholar
[13] Gao X N, Lou SY, Tang X Y 2013 J. High Energy Phys. 5 029
[14] Olver P J 1993 Applications of Lie Group to Differential Equations (2nd ed.) (New York: Springer) pp75–238
[15] Liu P, Zeng B Q, Ren B 2015 Commun. Theor. Phys. 63 413
Google Scholar
[16] Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202
Google Scholar
[17] Liu P, Zeng B Q, Deng B B, Yang J R 2015 AIP Adv. 5 087162
Google Scholar
[18] Liu P, Wang Y X, Ren B, Li J H 2016 Commun. Theor. Phys. 66 595
Google Scholar
[19] 焦小玉, 贾曼, 安红利 2019 物理学报 68 140201
Google Scholar
Jiao X Y, Jia M, An H L 2019 Acta Phys. Sin. 68 140201
Google Scholar
[20] Lou S Y 2015 Stud. Appl. Math. 134 372
Google Scholar
计量
- 文章访问数: 3860
- PDF下载量: 127
- 被引次数: 0
