-
Hydrogen maser uses the transition frequency of hydrogen atom at hyperfine energy level of ground state to realize precise timing. It has excellent frequency stability, especially in medium- and short-term, and low frequency drift. It has been used as high-precision frequency standard in engineering fields such as time keeping, navigation, and very long baseline interferometry. Clock transition of hydrogen maser is the transition between states of
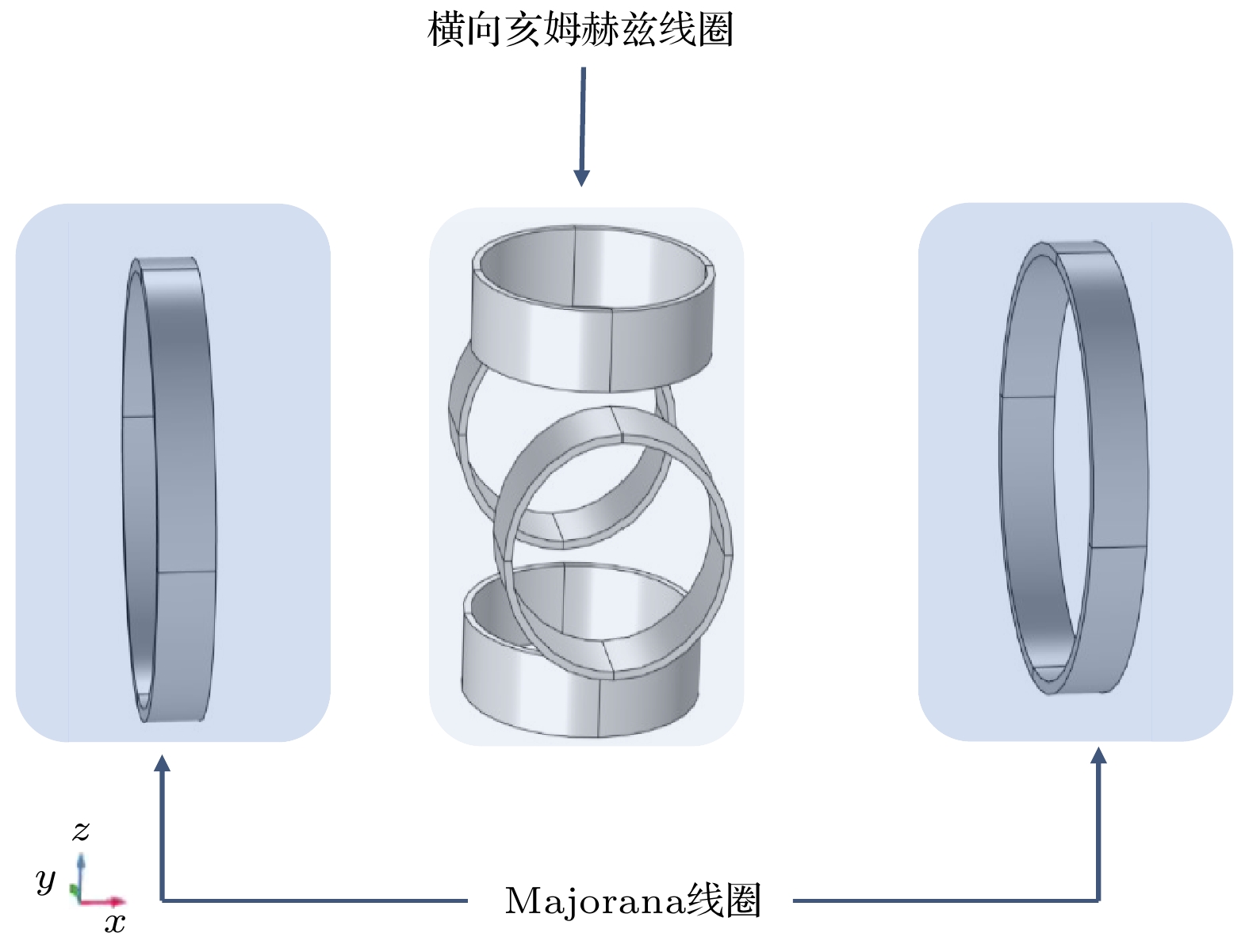
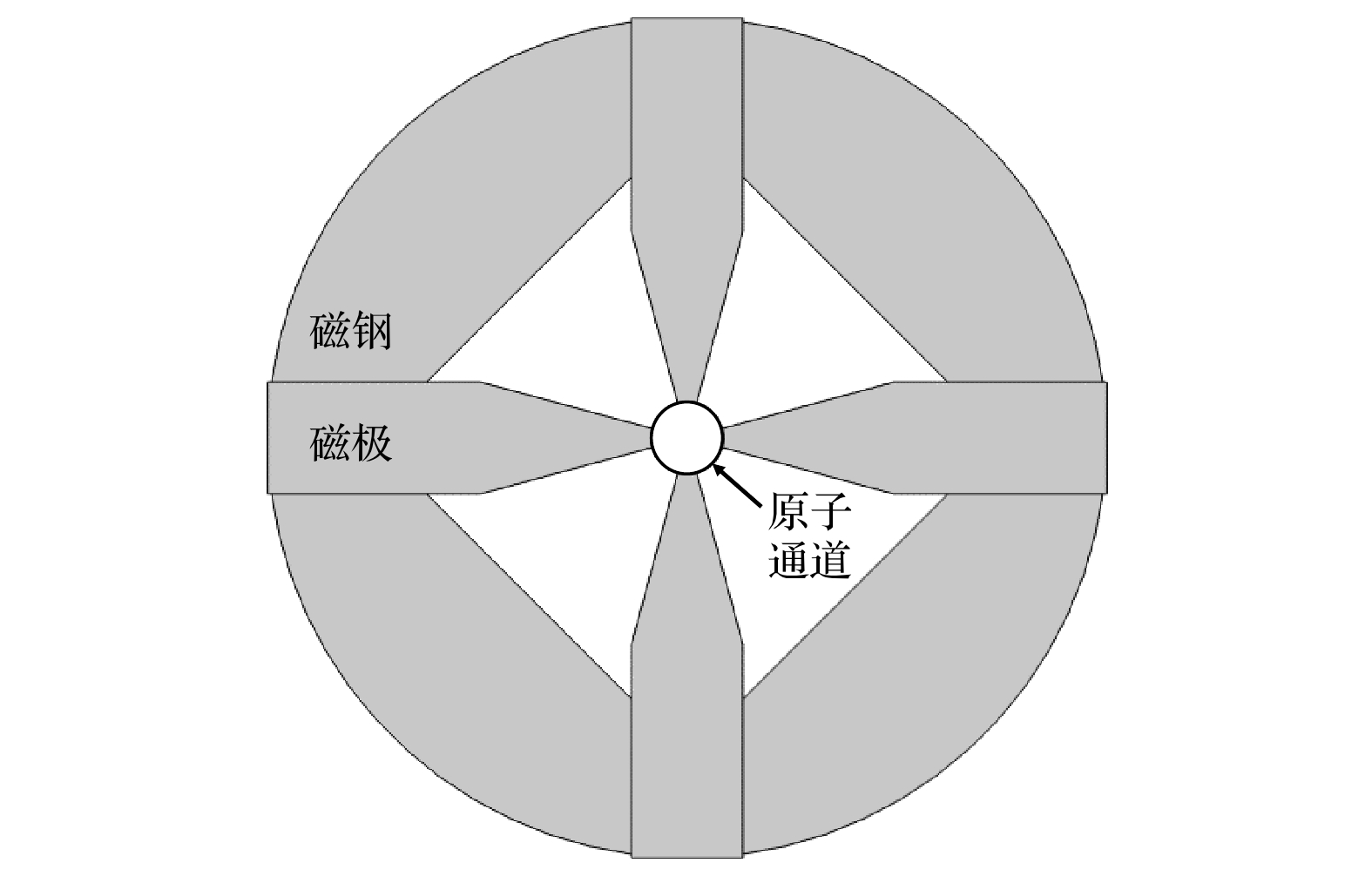
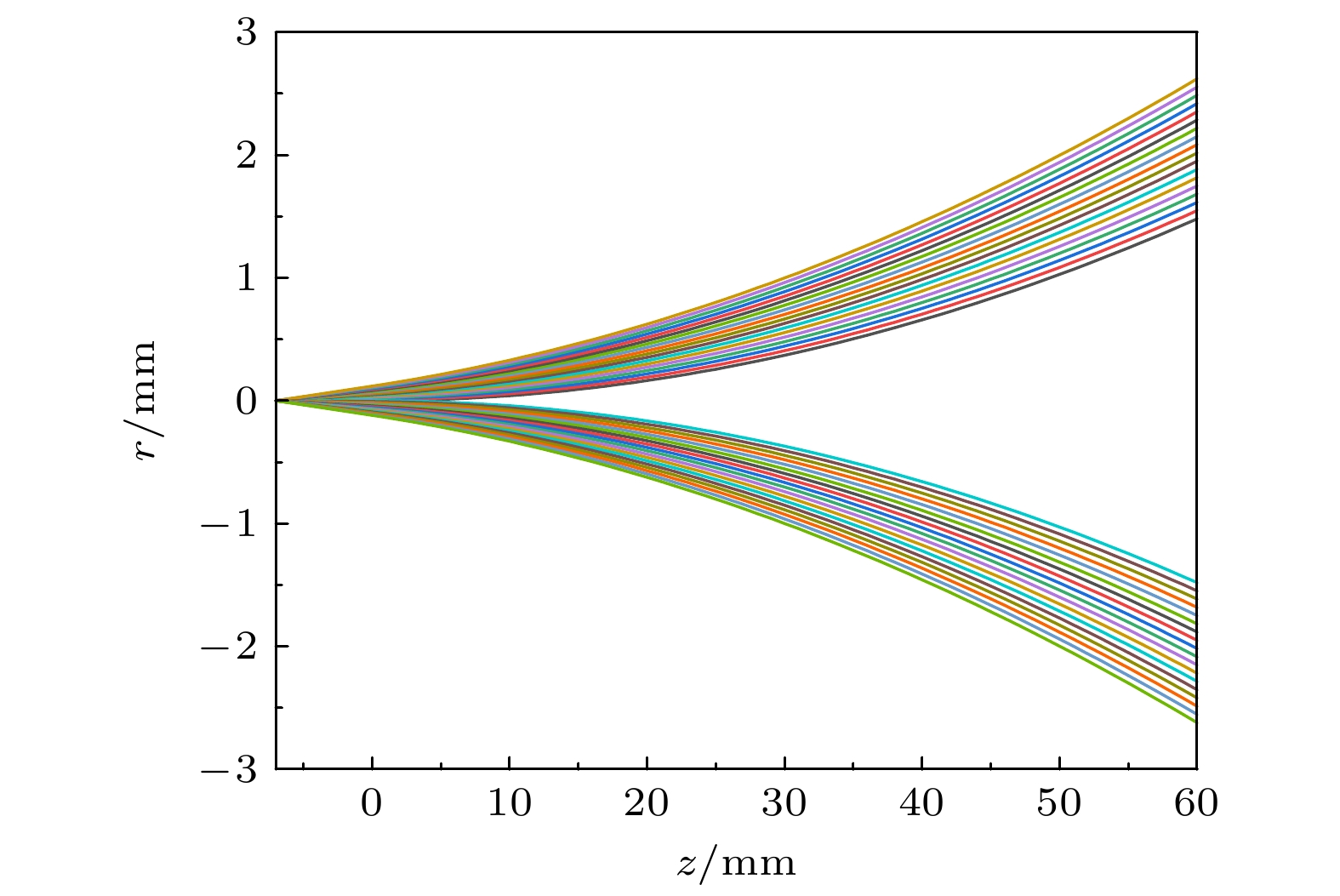
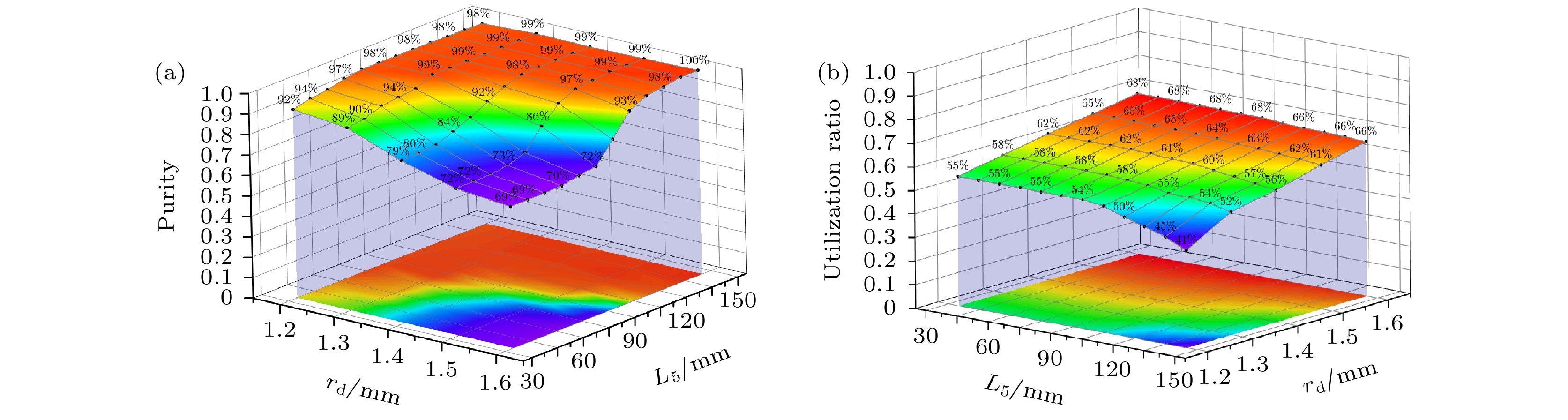
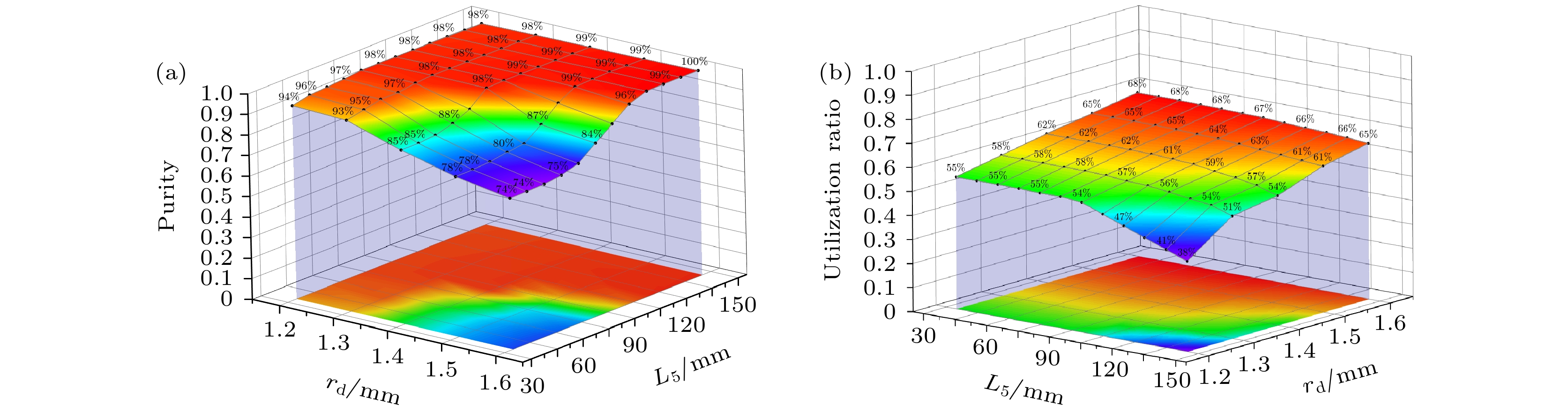
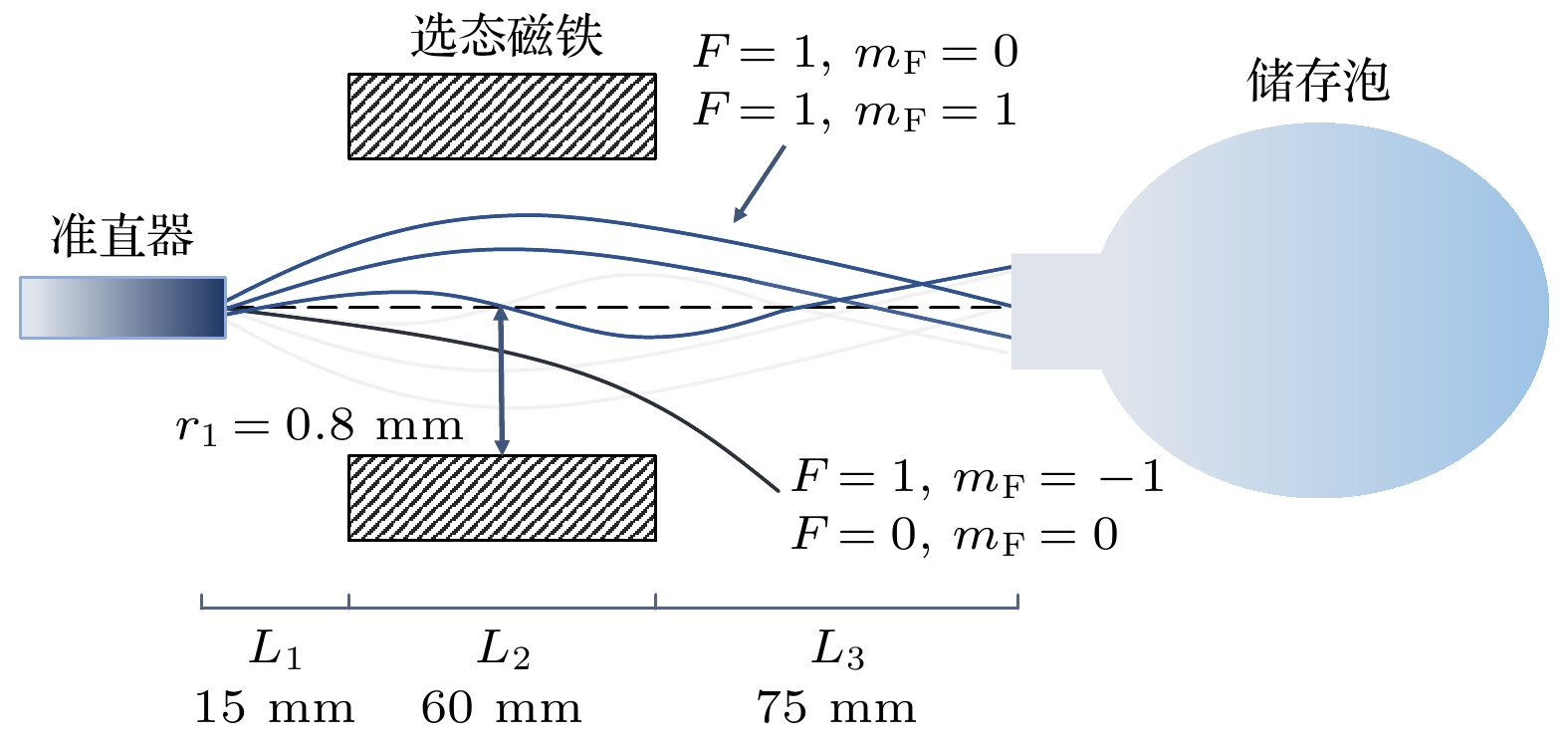
$|F = 1, m_{\rm F} = 0\rangle $ and$|F = 0, m_{\rm F} = 0\rangle $ . State selection is realized by state selection magnet, through which high energy atoms are converged and low energy atoms are dispersed. In conventional magnet state-selecting system, both atoms of$|F = 1, m_{\rm F} = 0\rangle $ states, which are required for the maser transition, and useless atoms of$|F = 1, m_{\rm F} = 1\rangle $ states are focused into storage bulb, which places restrictions on the medium- and long-term frequency stability performance of hydrogen maser. In order to further improve the quality of atomic transition spectral lines and the performance of hydrogen maser, double state-selection beam optical system which is based on the Majorana transition mode is constructed through calculations and simulations. In this work, we use Majorana method to invert atomic states. The magnetic field required for Majorana transition is established by using two coils with reverse current. The two coils are separated by 71 mm, and the coil axes are aligned with the direction of atomic beam. The other two pairs of transverse Helmholtz coils are separated by 22 mm in the center of the state reversal to adjust the zero point of magnetic field, which should coincide with the atomic beam to ensure a complete reversal of atomic polarity. The state reversal region is surrounded by four magnetic shields to reduce the influence of stray magnetic fields. Relationship between selected-state magnetic field gradient and distance of magnetic poles is analyzed by simulation, and trajectories of the atoms with high and low energy under different selected-state magnetic fields are calculated. The utilization and purity of high energy state atoms entering into bulb atoms are obtained. The purity of the selected$|F = 1, m_{\rm F} = 0\rangle $ state atoms reaches 99% and the utilization rate is 58%. This is ideal for engineering applications. It effectively enhances the proportion of$|F = 1, m_{\rm F} = 0\rangle $ state atoms entering into the atomic storage bulb and ensures the utilization of atoms. We verify the state-selection beam optical system experimentally. By turning on double state-selection system the maser signal can be enhanced. By adjusting the coil current of the double state-selection system, the maser signal varies with coil current, which verifies the effectiveness of double state-selection system.-
Keywords:
- hydrogen atomic clock /
- double state-selection /
- beam optical system
[1] Kleppner D, Goldenberg H M, Ramsey N F 1962 Phys. Rev. 126 603
Google Scholar
[2] Schmittberger B L, Scherer D R 2020 arXiv: 2004.09987 [atom-ph]
[3] Litvinov D A, Rudenko V N, Alakoz A V, Bach U, Zakhvatkin M V 2018 Phys. Lett. A 382 2192
Google Scholar
[4] Wu Z Q, Zhou S S, Hu X G, Liu L, Shuai T 2018 GPS Solutions 22 43
Google Scholar
[5] 王志超, 刘庆会, 郑鑫, 谢勇辉, 邓涛, 蒋健华, 张超, 王玲, 梁悦 2022 天文学报 63 21
Wang Z C, Liu Q H, Zheng X, Zhang J, Xie Y H, Deng T, Jiang J H, Zhang C, Wang L L, Liang Y 2022 Acta Astron. Sin. 63 21
[6] Ashby N, Heavner T P, Jefferts S R, Parker T E, Radnaev A G, Dudin Y O 2007 Phys. Rev. Lett. 98 070802
Google Scholar
[7] Vanier J, Audoin C 1989 The Quantum Physics of Atomic Frequency Standards (Bristol: Hilger) pp491–499
[8] 王义遒 1986 量子频标原理 (北京: 科学出版社) 第403—421页
Wang Y Q 1986 Quantum Frequency Scale Principle (Beijing: Science Press) pp403–421 (in Chinese)
[9] Shinji U, Yasusada O 1983 Jpn. J. Appl. Phys. 22 1009
Google Scholar
[10] Urabe S, Nakagiri K, Ohta Y, Kobayashi M, Saburi Y 1980 IEEE Trans. Instrum. Meas. 29 304
Google Scholar
[11] Humphrey M A, Phillips D F, Walsworth R L 2000 Phys. Rev. A 62 597
[12] Boyko A I, Aleynikov M S 2014 Meas. Tech. 56 1140
Google Scholar
[13] Mikhail A 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum Denver, CO, USA, April 12–16, 2015 p480
[14] Polyakov V, Belyaev A, Demidov A, Timofeev Y V 2018 Meas. Tech. 61 784
Google Scholar
[15] Polyakov V, Timofeev Y, Demidov A 2021 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium Electr Network, July 7–17, 2021 p2022-05-04
[16] Morris R J 1964 Phys. Rev. 133 A740
Google Scholar
[17] Mattison E M, Vessot FC R, S Wei 1987 Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on 34 622
Google Scholar
[18] 王义遒 1981 计量学报 1 44
Wang Y Q 1981 Acta Metrol. Sin. 1 44
[19] 王勇, 李建清, 邱实 2012 东南大学学报(自然科学版) 42 67
Google Scholar
Wang Y, Li J Q, Qiu S 2012 J. Southeast Univ. (Nat. Sci. Ed. ) 42 67
Google Scholar
[20] 谢勇辉, 戴家瑜, 林传富 2009 全国时间频率学术会议 四川成都, 10月22—24日, 2009年 第87页
Xie Y H, Dai J Y, Lin C F 2009 National Academic Conference on Time and Frequency Chengdu, Sichuan, October 22–24, 2009 p87 (in Chinese)
-
图 1 选态原理
Figure 1. Principle of state selection.
图 2 双选态示意图
Figure 2. Schematic diagram of the double state selection system.
图 3 氢原子能级布局数随P值的变化
Figure 3. Variation of hydrogen atomic energy level layout number with P value.
图 4 Majorana线圈与横向Helmholtz线圈位置示意图
Figure 4. Position diagram of Majorana coils and transverse Helmholtz coils.
图 5 四极选态磁铁示意图
Figure 5. Quadrupole state selective magnet.
图 6 (a) 仿真磁场示意图; (b) 不同磁极间距对应的磁场大小
Figure 6. (a) The simulated magnetic field; (b) the right figure shows the magnetic field of different magnetic poles.
图 7
$|F = 0, m_{\rm F} = 0\rangle $ 和$|F = 1, m_{\rm F} = -1\rangle $ 态原子在一级选态区运动轨迹Figure 7. Trajectories of
$|F = 0, m_{\rm F} = 0\rangle $ and$|F = 1, m_{\rm F} = $ $ -1\rangle $ state atoms in the first selected region.
图 8
$|F = 1, m_{\rm F} = 1\rangle $ 态和$|F = 1, m_{\rm F} = 0\rangle $ 态原子在一级选态区内运动轨迹Figure 8. Trajectories of
$|F = 1, m_{\rm F} = 1\rangle $ and$|F = 1, m_{\rm F} = $ $ 0\rangle $ state atoms in the first selected region.
图 9
$|F = 1, m_{\rm F} = 1\rangle $ 态和$|F = 1, m_{\rm F} = 0\rangle $ 态原子在二级选态区入口处偏转距离Figure 9.
$|F = 1, m_{\rm F} = 1\rangle $ and$|F = 1, m_{\rm F} = 0\rangle $ state atoms deflection distance at the entrance of the secondary selected region.
图 10 束光学系统三维模型
Figure 10. The model of beam optical system.
图 11 L4 = 60 mm, 不同rd和L5下的原子纯度和利用率 (a) 原子纯度; (b) 原子利用率
Figure 11. Atomic purity and utilization under different rd and L5 at L4 = 60 mm: (a) Atomic purity; (b) atomic utilization.
图 12 L4 = 70 mm, 不同rd和L5下的原子纯度和利用率 (a)原子纯度; (b)原子利用率
Figure 12. At L4 = 70 mm, atomic purity and utilization under different rd and L5: (a) Atomic purity; (b) atomic utilization on the right.
图 13 L4 = 75 mm, 不同rd和L5下的原子纯度和利用率 (a) 原子纯度; (b) 原子利用率
Figure 13. At L4 = 75 mm, atomic purity and utilization under different rd and L5: (a) Atomic purity; (b) atomic utilization.
图 14 L4 = 80 mm, 不同rd和L5下的原子纯度和利用率 (a) 原子纯度; (b) 原子利用率
Figure 14. At L4 = 80 mm, atomic purity and utilization under different rd and L5: (a) Atomic purity; (b) atomic utilization.
图 15 在储存泡口截面处原子点密度图
Figure 15. Point density diagram of atoms at entrance of storage bulb.
图 16 在一对线圈电流Ix = –0.5 mA的固定值下, 氢原子钟输出功率与Iy的依赖关系
Figure 16. The Hydrogen atomic clock’s output power dependence on the current of the transverse pair Iy under fixed value of the another pair’s current Ix = –0.5 mA.
图 17 改变两对线圈电流, 氢原子钟输出功率变化
Figure 17. The Hydrogen atomic clock’s output power dependence on the both coil pair’s currents.
表 1 磁场梯度与磁极间距对应关系
Table 1. Correspondence between magnetic field gradient and magnetic pole spacing.
磁极间距/mm 0.8 1 1.2 1.3 1.4 1.5 1.6 1.8 2 $ \dfrac{B}{{{r_{\text{d}}}}} $/(T·mm–1) 1.167 0.850 0.625 0.557 0.510 0.456 0.405 0.367 0.303 
DownLoad: CSV
表 2 L4 = 60 mm时, 不同L5和rd原子偏转概率
Table 2. Different L5 and rd atomic deflection probabilities at L4 = 60 mm.
rd/mm L5/mm 60 70 80 90 100 110 120 130 140 150 1.2 80.1% 84.2% 88.5% 96.8% 99.4% 100.0% 100.0% 100.0% 100.0% 100.0% 1.3 71.2% 75.0% 76.0% 85.9% 91.0% 98.8% 100.0% 100.0% 100.0% 100.0% 1.4 65.5% 70.5% 72.5% 75.2% 85.7% 91.2% 95.2% 99.7% 100.0% 100.0% 1.5 61.5% 64.2% 65.2% 69.6% 75.0% 81.7% 88.2% 93.9% 96.5% 99.4% 1.6 57.2% 58.6% 61.2% 67.5% 69.5% 73.4% 77.5% 83.0% 88.3% 93.0%
DownLoad: CSV
表 3 L4 = 70 mm时, 不同L5和rd原子偏转概率
Table 3. Different L5 and rd atomic deflection probabilities at L4 = 70 mm.
rd/mm L5/mm 60 70 80 90 100 110 120 130 140 150 1.2 94.5% 96.1% 100.0% 100.0% 92.3% 97.6% 99.7% 100.0% 100.0% 100.0% 1.3 86.7% 88.0% 96.8% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 1.4 76.0% 79.0% 88.2% 96.1% 99.5% 100.0% 100.0% 100.0% 100.0% 100.0% 1.5 71.2% 73.6% 76.6% 84.8% 91.3% 97.6% 99.7% 100.0% 100.0% 100.0% 1.6 66.2% 67.2% 71.2% 79.7% 84.8% 88.3% 93.1% 97.4% 100.0% 100.0%
DownLoad: CSV
表 4 L4 = 80 mm时, 不同L5和rd原子偏转概率
Table 4. Different L5 and rd atomic deflection probabilities at L4 = 80 mm.
rd/mm L5/mm 60 70 80 90 100 110 120 130 140 150 1.2 99.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 1.3 97.8% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 1.4 89.5% 92.3% 97.2% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% 1.5 82.9% 83.5% 87.8% 93.4% 98.7% 100.0% 100.0% 100.0% 100.0% 100.0% 1.6 76.2% 78.2% 82.3% 90.1% 95.4% 98.2% 100.0% 100.0% 100.0% 100.0%
DownLoad: CSV
-
[1] Kleppner D, Goldenberg H M, Ramsey N F 1962 Phys. Rev. 126 603
Google Scholar
[2] Schmittberger B L, Scherer D R 2020 arXiv: 2004.09987 [atom-ph]
[3] Litvinov D A, Rudenko V N, Alakoz A V, Bach U, Zakhvatkin M V 2018 Phys. Lett. A 382 2192
Google Scholar
[4] Wu Z Q, Zhou S S, Hu X G, Liu L, Shuai T 2018 GPS Solutions 22 43
Google Scholar
[5] 王志超, 刘庆会, 郑鑫, 谢勇辉, 邓涛, 蒋健华, 张超, 王玲, 梁悦 2022 天文学报 63 21
Wang Z C, Liu Q H, Zheng X, Zhang J, Xie Y H, Deng T, Jiang J H, Zhang C, Wang L L, Liang Y 2022 Acta Astron. Sin. 63 21
[6] Ashby N, Heavner T P, Jefferts S R, Parker T E, Radnaev A G, Dudin Y O 2007 Phys. Rev. Lett. 98 070802
Google Scholar
[7] Vanier J, Audoin C 1989 The Quantum Physics of Atomic Frequency Standards (Bristol: Hilger) pp491–499
[8] 王义遒 1986 量子频标原理 (北京: 科学出版社) 第403—421页
Wang Y Q 1986 Quantum Frequency Scale Principle (Beijing: Science Press) pp403–421 (in Chinese)
[9] Shinji U, Yasusada O 1983 Jpn. J. Appl. Phys. 22 1009
Google Scholar
[10] Urabe S, Nakagiri K, Ohta Y, Kobayashi M, Saburi Y 1980 IEEE Trans. Instrum. Meas. 29 304
Google Scholar
[11] Humphrey M A, Phillips D F, Walsworth R L 2000 Phys. Rev. A 62 597
[12] Boyko A I, Aleynikov M S 2014 Meas. Tech. 56 1140
Google Scholar
[13] Mikhail A 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum Denver, CO, USA, April 12–16, 2015 p480
[14] Polyakov V, Belyaev A, Demidov A, Timofeev Y V 2018 Meas. Tech. 61 784
Google Scholar
[15] Polyakov V, Timofeev Y, Demidov A 2021 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium Electr Network, July 7–17, 2021 p2022-05-04
[16] Morris R J 1964 Phys. Rev. 133 A740
Google Scholar
[17] Mattison E M, Vessot FC R, S Wei 1987 Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on 34 622
Google Scholar
[18] 王义遒 1981 计量学报 1 44
Wang Y Q 1981 Acta Metrol. Sin. 1 44
[19] 王勇, 李建清, 邱实 2012 东南大学学报(自然科学版) 42 67
Google Scholar
Wang Y, Li J Q, Qiu S 2012 J. Southeast Univ. (Nat. Sci. Ed. ) 42 67
Google Scholar
[20] 谢勇辉, 戴家瑜, 林传富 2009 全国时间频率学术会议 四川成都, 10月22—24日, 2009年 第87页
Xie Y H, Dai J Y, Lin C F 2009 National Academic Conference on Time and Frequency Chengdu, Sichuan, October 22–24, 2009 p87 (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 2045
- PDF Downloads: 41
- Cited By: 0
