-
针对偶极相互作用的玻色-爱因斯坦凝聚体, 解析计算了点状杂质沿平行极化轴和垂直极化轴运动的能量耗散率, 证明了在超流临界速度更大的方向上耗散率也更高. 该结论为最近在162Dy原子气体中观测到的实验现象提供了理论支持. 对于一般的运动方向, 给出了耗散率在高速极限下以及临界速度附近的渐近形式. 结合数值计算的结果, 论证了耗散率随方向角的变化总是表现出与临界速度一致的各向异性.
-
关键词:
- 偶极玻色-爱因斯坦凝聚体 /
- 各向异性超流 /
- 朗道临界速度 /
- 耗散
The ability to support frictionless motion is one of the manifestations of superfluidity. An impurity immersed in a superfluid can move without dissipation below the critical velocity, which, according to the Landau criterion, is determined by the elementary excitation spectrum of the system. In a quantum gas of the ultracold atoms, the critical velocity can be measured by stirring a laser beam through the atomic cloud, and the emergence of dissipation can be observed via the heating effect above the threshold stirring speed. Recently, such a technique is exploited to study the superfluidity of the Bose-Einstein condensate (BEC) of 162Dy atoms with dipole-dipole interactions. It is shown that both the critical velocity and the heating rate reflect the anisotropy of the underlying dipolar excitation spectrum. In this work, we theoretically investigate the anisotropic dissipation of a point-like impurity moving through a dipolar BEC. For the motion along the principal axis, the dissipation rate above the critical velocity is analytically derived according to the linear response theory. At a given reduced velocity, we find the dissipation rate being of a higher value in the direction parallel to the dipole moment, which qualitatively explains the recent experimental observation in dysprosium atoms. Moreover, in the moving direction away from the principal axis, the asymptotic expressions for the dissipation rate are obtained in the high-speed limit, as well as in the regime close to the dissipation threshold. By combining these analytical results with the numerical calculations, we conclude that, in a dipolar BEC, the angular dependence of the dissipation rate always shows the same anisotropy as the critical velocity. Our predictions can be examined in the current experiments with cold atoms, and the results presented here may be also helpful in understanding the anisotropic superfluidity in other systems. -
Keywords:
- dipolar Bose-Einstein condensate /
- anisotropic superfluidity /
- Landau critical velocity /
- dissipation
[1] Landau L D 1941 Phys. Rev. 60 356
Google Scholar
[2] Landau L D 1941 J. Phys. USSR 5 71
[3] Raman C, Köhl M, Onofrio R, Durfee D S, Kuklewicz C E, Hadzibabic Z, Ketterle W 1999 Phys. Rev. Lett. 83 2502
Google Scholar
[4] Onofrio R, Raman C, Vogels J M, Abo-Shaeer J R, Chikkatur A P, Ketterle W 2000 Phys. Rev. Lett. 85 2228
Google Scholar
[5] Desbuquois R, Chomaz L, Yefsah T, Léonard J, Beugnon J, Weitenberg C, Dalibard J 2012 Nat. Phys. 8 645
Google Scholar
[6] Miller D E, Chin J K, Stan C A, Liu Y, Setiawan W, Sanner C, Ketterle W 2007 Phys. Rev. Lett. 99 070402
Google Scholar
[7] Weimer W, Morgener K, Singh V P, Siegl J, Hueck K, Luick N, Mathey L, Moritz H 2015 Phys. Rev. Lett. 114 095301
Google Scholar
[8] Wenzel M, Böttcher F, Schmidt J N, Eisenmann M, Langen T, Pfau T, Ferrier-Barbut I 2018 Phys. Rev. Lett. 121 030401
Google Scholar
[9] Griesmaier A, Werner J, Hensler S, Stuhler J, Pfau T 2005 Phys. Rev. Lett. 94 160401
Google Scholar
[10] Lu M, Burdick N Q, Youn S H, Lev B L 2011 Phys. Rev. Lett. 107 190401
Google Scholar
[11] Aikawa K, Frisch A, Mark M, Baier S, Rietzler A, Grimm R, Ferlaino F 2012 Phys. Rev. Lett. 108 210401
Google Scholar
[12] Pitaevskii L P, Stringari S 2016 Bose-Einstein Condensation and Superfluidity (New York: Oxford University Press) pp89–91
[13] Yu Z Q 2017 Phys. Rev. A 95 033618
Google Scholar
[14] Baranov M A 2008 Phys. Rep. 464 71
Google Scholar
[15] Lahaye T, Menotti C, Santos L, Lewenstein M, Pfau T 2009 Rep. Prog. Phys. 72 126401
Google Scholar
[16] Volovik G E 2009 The Universe in a Helium Droplet (New York: Oxford University Press) pp321–322
[17] Kovrizhin D L, Maksimov L A 2001 Phys. Lett. A 282 421
Google Scholar
[18] Astrakharchik G E, Pitaevskii L P 2004 Phys. Rev. A 70 013608
Google Scholar
[19] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[20] Goldman N, Juzeliūnas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401
Google Scholar
[21] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
-
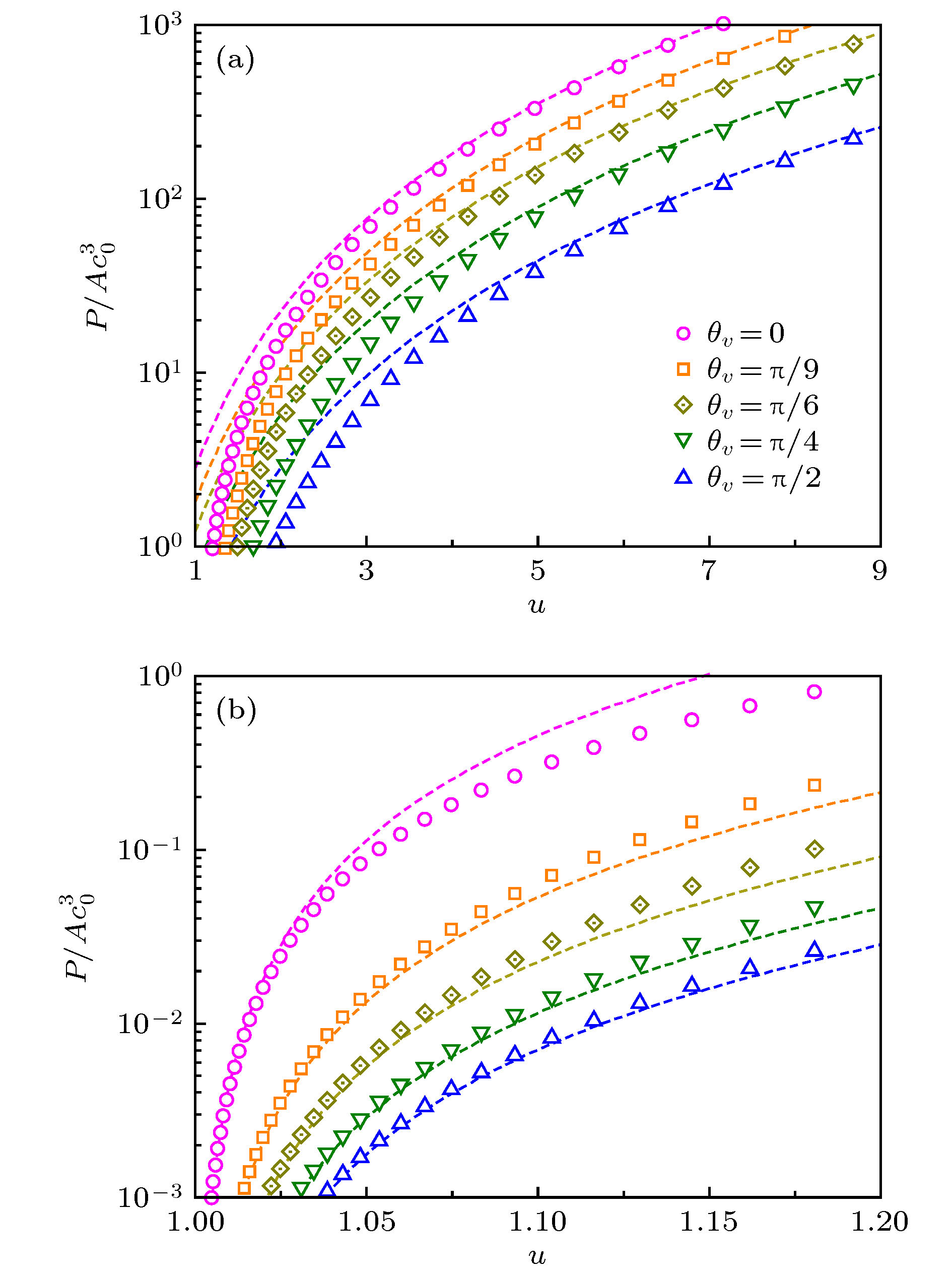
图 1 沿不同方向的能量耗散率P在(a)高耗散区间和(b)低耗散区间随约化速度u的变化曲线. 离散点为数值计算的结果, (a)和(b)中的虚线分别对应于(8)式和(9)式给出的渐近表达式. 从上至下, 各曲线的临界速度分别为 vc = 1.41c0, 1.22c0, 1.07c0, 0.89c0, 0.71c0. 两图采用的图例相同. 偶极相互作用参数取为
$ \epsilon_{\rm{dd}}=0.5 $ Fig. 1. Energy dissipation rate P as a function of reduced velocity u along different directions in (a) high dissipation regime and (b) low dissipation regime. Discrete symbols are numerical results, and dashed lines in (a) and (b) correspond to the asymptotic expressions (8) and (9), respecti-vely. From up to bottom, the critical velocities for each line are given by vc = 1.41c0, 1.21c0, 1.07c0, 0.89c0, and 0.71c0. The two plots use the same legend. The relative strength of dipolar interaction is set as
$ \epsilon_{\rm{dd}}=0.5 $ . -
[1] Landau L D 1941 Phys. Rev. 60 356
Google Scholar
[2] Landau L D 1941 J. Phys. USSR 5 71
[3] Raman C, Köhl M, Onofrio R, Durfee D S, Kuklewicz C E, Hadzibabic Z, Ketterle W 1999 Phys. Rev. Lett. 83 2502
Google Scholar
[4] Onofrio R, Raman C, Vogels J M, Abo-Shaeer J R, Chikkatur A P, Ketterle W 2000 Phys. Rev. Lett. 85 2228
Google Scholar
[5] Desbuquois R, Chomaz L, Yefsah T, Léonard J, Beugnon J, Weitenberg C, Dalibard J 2012 Nat. Phys. 8 645
Google Scholar
[6] Miller D E, Chin J K, Stan C A, Liu Y, Setiawan W, Sanner C, Ketterle W 2007 Phys. Rev. Lett. 99 070402
Google Scholar
[7] Weimer W, Morgener K, Singh V P, Siegl J, Hueck K, Luick N, Mathey L, Moritz H 2015 Phys. Rev. Lett. 114 095301
Google Scholar
[8] Wenzel M, Böttcher F, Schmidt J N, Eisenmann M, Langen T, Pfau T, Ferrier-Barbut I 2018 Phys. Rev. Lett. 121 030401
Google Scholar
[9] Griesmaier A, Werner J, Hensler S, Stuhler J, Pfau T 2005 Phys. Rev. Lett. 94 160401
Google Scholar
[10] Lu M, Burdick N Q, Youn S H, Lev B L 2011 Phys. Rev. Lett. 107 190401
Google Scholar
[11] Aikawa K, Frisch A, Mark M, Baier S, Rietzler A, Grimm R, Ferlaino F 2012 Phys. Rev. Lett. 108 210401
Google Scholar
[12] Pitaevskii L P, Stringari S 2016 Bose-Einstein Condensation and Superfluidity (New York: Oxford University Press) pp89–91
[13] Yu Z Q 2017 Phys. Rev. A 95 033618
Google Scholar
[14] Baranov M A 2008 Phys. Rep. 464 71
Google Scholar
[15] Lahaye T, Menotti C, Santos L, Lewenstein M, Pfau T 2009 Rep. Prog. Phys. 72 126401
Google Scholar
[16] Volovik G E 2009 The Universe in a Helium Droplet (New York: Oxford University Press) pp321–322
[17] Kovrizhin D L, Maksimov L A 2001 Phys. Lett. A 282 421
Google Scholar
[18] Astrakharchik G E, Pitaevskii L P 2004 Phys. Rev. A 70 013608
Google Scholar
[19] Galitski V, Spielman I B 2013 Nature 494 49
Google Scholar
[20] Goldman N, Juzeliūnas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401
Google Scholar
[21] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
下载:
计量
- 文章访问数: 6331
- PDF下载量: 122
- 被引次数: 0
