-
The fractal is a kind of geometric figure with self-similar character. Phase transition and critical phenomenon of spin model on fractal lattice have been widely studied and many interesting results have been obtained. The
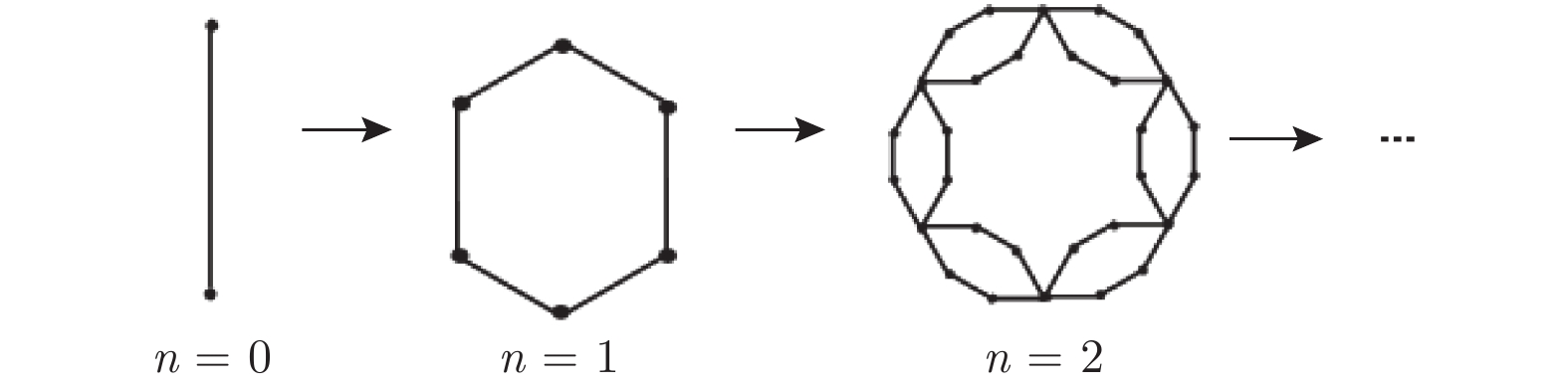
${S^4}$ model regarded as an extension of the Ising model, can take a continuous spin value. Research of the${S^4}$ model can give a better understanding of the phase transition in the real ferromagnetic system in nature. In previous work, the phase transition of the${S^4}$ model on the translation symmetry lattice has been studied with the momentum space renormalization group technique. It is found that the number of the fixed points is related to the space dimensionality. In this paper, we generate a family of diamond hierarchical lattices. The lattice is a typical inhomogenous fractal with self-similar character, whose fractal dimensionality and the order of ramification are${d_{\rm{f}}} = {\rm{1}} + \ln m/\ln {\rm{3}}$ and$R = \infty $ , respectively. In order to discuss the phase transition of the${S^4}$ model on the lattice, we assume that the Gaussian distribution constant${b_i}$ and the fourth-order interaction parameter${u_i}$ depend on the coordination number${q_i}$ of the site on the fractal lattices, and the relation${b_i}/{b_j} = {u_i}/{u_j} = {q_i}/{q_j}$ is satisfied. Using the renormalization group and the cumulative expansion method, we study the phase transition of the${S^4}$ model on a family of diamond lattices of$m$ branches. Removing the inner sites, we obtain the system recursion relation and the system corresponding critical point. Furthermore, we find that if the number of branches is$m = 2$ or$m > {\rm{1}}2$ (fractal dimensionality${d_{\rm{f}}} = {\rm{1}}{\rm{.63}}$ or${d_{\rm{f}}} > {\rm{3}}{\rm{.26}}$ ), the system only has the Gaussian fixed point of${K^ * } = {b_2}/2$ ,$u_2^ * = 0$ . The critical point of the system is in agreement with that from the Gaussian model on the fractal lattice, which predicts that the two systems belong to the same university class. We also find that under the condition of${\rm{3}} \leqslant m \leqslant {\rm{1}}2$ (fractal dimensionality${\rm{2}} \leqslant {d_{\rm f}} \leqslant {\rm{3}}{\rm{.26}}$ ), both the Gaussian fixed point and the Wilson-Fisher fixed point can be obtained in the system, and the Wilson-Fisher fixed point plays a leading role in the critical properties of the system. According to the real space renormalization group transformation and scaling theory, we obtain the critical exponent of the correlation length. Finally, we find that the critical points of the${S^4}$ model on a family of diamond lattices depend on the value of the fractal dimensionality. The above result is similar to that obtained from the${S^4}$ model on the translation symmetry lattice.-
Keywords:
- diamond lattice /
- S4 model /
- renormalization-group
[1] Gefen Y, Mandelbrot B, Aharony A 1980 Phys. Rev. Lett. 45 855
 Google Scholar
Google Scholar
[2] Gefen Y, Aharony A, Mandelbrot B 1983 J. Phys. A 16 1267
 Google Scholar
Google Scholar
[3] Gefen Y, Aharony A, Mandelbrot B 1984 J. Phys. A 17 435
 Google Scholar
Google Scholar
[4] Gefen Y, Aharony A, Mandelbrot B 1984 J. Phys. A 17 1277
 Google Scholar
Google Scholar
[5] Hu B 1985 Phys. Rev. Lett. 55 2316
 Google Scholar
Google Scholar
[6] Wang Z D, Gong C D, Arno H 1986 Phys. Rev. A 34 1531
 Google Scholar
Google Scholar
[7] Wu Y K, Hu B 1987 Phys. Rev. A 35 1404
 Google Scholar
Google Scholar
[8] Fahnle M, Braun P 1988 Phys. Rev. B 38 7094
 Google Scholar
Google Scholar
[9] Yang Z R 1988 Phys. Rev. B 38 728
 Google Scholar
Google Scholar
[10] Qin Y, Yang Z R 1992 Phys. Rev. B 46 284
[11] Li S, Yang Z R 1997 Phys. Rev. E 55 6656
 Google Scholar
Google Scholar
[12] Zhu J Y, Yang Z R 1997 Phys. Rev. E 59 1551
[13] Kong X M, Li S 1999 Sci. China A 42 325
[14] Lin Z Q, Kong X M 2001 Chin. Phys. Lett. 18 882
[15] Zhu J Y, Zhu H 2003 Chin. Phys. 12 264
 Google Scholar
Google Scholar
[16] 孙春峰 2005 物理学报 54 3768
 Google Scholar
Google Scholar
Sun C F 2005 Acta Phys. Sin. 54 3768
 Google Scholar
Google Scholar
[17] Li Y, Kong X M 2005 Physica A 356 589
 Google Scholar
Google Scholar
[18] Sun C F, Kong X M, Yin X C 2006 Commun. Theor. Phys. 45 555
 Google Scholar
Google Scholar
[19] Chen X, Zhang J S 2014 Chin. Phys. B 23 096401
 Google Scholar
Google Scholar
[20] 尹训昌, 刘万芳, 祝祖送, 孔祥木 2015 物理学报 64 016402
 Google Scholar
Google Scholar
Yin X C, Liu W F, Zhu Z S, Kong X M 2015 Acta Phys. Sin. 64 016402
 Google Scholar
Google Scholar
[21] 陈克萍, 吕鹏, 王海鹏 2017 物理学报 66 068101
 Google Scholar
Google Scholar
Chen K P, Lü P, Wang H P 2017 Acta Phys. Sin. 66 068101
 Google Scholar
Google Scholar
-
表 1 mDH晶格上
${S^4}$ 模型的Wilson-Fisher不动点和关联长度$\nu $ 的数值Table 1. Wilson-Fisher fixed point of
${S^4}$ model on mDH lattices and the value of correlation length$\nu $ .$m$ ${K^ * }/{b_2}$ $u_2^ * /b_2^2$ $\nu $ 3 $0.484$ $0.017$ 0.465 4 $0.508$ $0.012$ 0.465 5 $0.515$ $0.010$ 0.467 6 $0.518$ $0.009$ 0.471 7 $0.520$ $0.008$ 0.477 8 $0.521$ $0.007$ 0.485 9 $0.521$ $0.006$ 0.489 10 $0.520$ $0.005$ 0.497 11 $0.517$ $0.004$ 0.488 12 $0.512$ $0.002$ 0.506 -
[1] Gefen Y, Mandelbrot B, Aharony A 1980 Phys. Rev. Lett. 45 855
 Google Scholar
Google Scholar
[2] Gefen Y, Aharony A, Mandelbrot B 1983 J. Phys. A 16 1267
 Google Scholar
Google Scholar
[3] Gefen Y, Aharony A, Mandelbrot B 1984 J. Phys. A 17 435
 Google Scholar
Google Scholar
[4] Gefen Y, Aharony A, Mandelbrot B 1984 J. Phys. A 17 1277
 Google Scholar
Google Scholar
[5] Hu B 1985 Phys. Rev. Lett. 55 2316
 Google Scholar
Google Scholar
[6] Wang Z D, Gong C D, Arno H 1986 Phys. Rev. A 34 1531
 Google Scholar
Google Scholar
[7] Wu Y K, Hu B 1987 Phys. Rev. A 35 1404
 Google Scholar
Google Scholar
[8] Fahnle M, Braun P 1988 Phys. Rev. B 38 7094
 Google Scholar
Google Scholar
[9] Yang Z R 1988 Phys. Rev. B 38 728
 Google Scholar
Google Scholar
[10] Qin Y, Yang Z R 1992 Phys. Rev. B 46 284
[11] Li S, Yang Z R 1997 Phys. Rev. E 55 6656
 Google Scholar
Google Scholar
[12] Zhu J Y, Yang Z R 1997 Phys. Rev. E 59 1551
[13] Kong X M, Li S 1999 Sci. China A 42 325
[14] Lin Z Q, Kong X M 2001 Chin. Phys. Lett. 18 882
[15] Zhu J Y, Zhu H 2003 Chin. Phys. 12 264
 Google Scholar
Google Scholar
[16] 孙春峰 2005 物理学报 54 3768
 Google Scholar
Google Scholar
Sun C F 2005 Acta Phys. Sin. 54 3768
 Google Scholar
Google Scholar
[17] Li Y, Kong X M 2005 Physica A 356 589
 Google Scholar
Google Scholar
[18] Sun C F, Kong X M, Yin X C 2006 Commun. Theor. Phys. 45 555
 Google Scholar
Google Scholar
[19] Chen X, Zhang J S 2014 Chin. Phys. B 23 096401
 Google Scholar
Google Scholar
[20] 尹训昌, 刘万芳, 祝祖送, 孔祥木 2015 物理学报 64 016402
 Google Scholar
Google Scholar
Yin X C, Liu W F, Zhu Z S, Kong X M 2015 Acta Phys. Sin. 64 016402
 Google Scholar
Google Scholar
[21] 陈克萍, 吕鹏, 王海鹏 2017 物理学报 66 068101
 Google Scholar
Google Scholar
Chen K P, Lü P, Wang H P 2017 Acta Phys. Sin. 66 068101
 Google Scholar
Google Scholar
计量
- 文章访问数: 8785
- PDF下载量: 54
- 被引次数: 0



































 下载:
下载:





