-
In classic statistical physics, an isolated system corresponds to a constant energy shell in the phase space, which can be described by the microcanonical ensemble. While, for an isolated quantum system, the conventional treatment is to subject the system to a narrow energy window in the Hilbert space instead of the energy shell in classical phase space, and then confine the participating eigen states of system wave function in the narrow window, so that the microcanonical ensemble can be recovered in the framework of quantum mechanics. Apart from the traditional theory, there is a more self-consistent description for the isolated quantum system, that is, the quantum microcanonical (QMC) ensemble. The QMC ensemble abandons the narrow energy window assumption, and allows all the eigen states to contribute to the system wave function on condition that the system average energy is fixed at a given value. At the same time, the total occupation probability of these eigen states is conserved to unity. The most probable probability distribution obtained in the Hilbert space for an isolated quantum system according to the constraints specified above is called the QMC statistics. There is a clear difference between the QMC distribution and the traditional Gibbs distribution having an exponential form. Through the external periodic drives, an isolated quantum system may produce the QMC distribution, which is a consequence of the interplay between internal origins and external drives. In this paper, we investigate the conditions for the formation and suppression of QMC distribution by using the exact diagonalization method based on the one-dimensional Ising model. We start with the one-dimensional Ising model and focus on three different cases of periodic drives: systems under vertical (along the z axis), horizontal (along the x axis), horizontal magnetic field together with random internal (along the y axis) magnetic field. For all these three cases, the external magnetic fields are set to be ordinary rectangular pulses and the Gibbs distributions are taken as the initial states. We then study the evolutions and their asymptotic tendencies to the QMC distributions of the eigen state occupation probability under the effect of external periodic magnetic field. The results show that under the vertical magnetic field, the eigen state occupation probability does not change, and the system cannot produce the QMC distribution; under the horizontal magnetic field, the system tends to display a QMC distribution, but only partly; under horizontal and random internal magnetic fields at the same time, the transition to QMC distribution can be fully realized, and finally the system is almost completely thermalized. In order to clarify the different behaviors of the Ising model in the three cases, we also calculate the information entropy of the eigen state of Floquet operator in the eigen representation of the unperturbed Hamiltonian. We find that as the information entropy of the Floquet eigen state increases, the convergence to the QMC distribution in the Hilbert space is improved. We also notice that the mechanism for the emergence of QMC distribution is closely related to the thermalization effect of the isolated quantum system. Our analyses show that when the magnetic field is vertical, it cannot trigger the thermalization of the system. When the magnetic field is horizontal, the system becomes partly, but not completely, thermalized. When we add a horizontal periodic magnetic field and a random internal magnetic field at the same time, the system can be completely thermalized to infinite temperature. Thus, the asymptotic behavior towards the QMC statistics is a reflection of the fact that the isolated quantum system is thermalizable under periodic drives.
-
Keywords:
- micro-canonical ensemble /
- Ising model /
- Floquet representation /
- thermalization
[1] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[2] Tomza M, Jachymski K, Gerritsma R, Negretti A, Calarco T, Idziaszek Z, Julienne P S 2019 Rev. Mod. Phys. 91 035001
Google Scholar
[3] Shi F, Kong X, Wang P, Kong F, Zhao N, Liu R B, Du J 2014 Nat. Phys. 10 21
Google Scholar
[4] Gao W B, Imamoglu A, Bernien H, Hanson R 2015 Nat. Photonics 9 363
Google Scholar
[5] Huang K 1987 Statistical Mechanics (New York: Wiley) pp131–135
[6] Pathria R K, Beale P D 2011 Statistical Mechanics (3rd Ed.) (Boston: Academic) pp115–119
[7] Popescu S, Short A J, Winter A 2006 Nat. Phys. 2 754
Google Scholar
[8] Goldstein S, Lebowitz J L, Tumulka R, Zanghì N 2006 Phys. Rev. Lett. 96 050403
Google Scholar
[9] Reimann P 2007 Phys. Rev. Lett. 99 160404
Google Scholar
[10] Mahler G, Gemmer J, Michel M 2005 Physica E 29, 53
Google Scholar
[11] Levine R D 1988 J. Stat. Phys. 52 1203
Google Scholar
[12] Buch V, Gerber R B, Ratner M A 1982 J. Chem. Phys. 76 5397
Google Scholar
[13] Brody D C, Hughston L P 1998 J. Math. Phys. 39 6502
Google Scholar
[14] Bender C M, Brody D C, Hook D W 2005 J. Phys. A: Math. Gen. 38 L607
Google Scholar
[15] Naudts J, Van der Straeten E 2006 J. Stat. Mech.: Theory Exp. 2006 06015
Google Scholar
[16] Fine B V 2009 Phys. Rev. E 80 051130
Google Scholar
[17] Campisi M 2013 New J. Phys. 15 115008
Google Scholar
[18] Ji K, Fine B V 2011 Phys. Rev. Lett. 107 050401
Google Scholar
[19] D'Alessio L, Rigol M 2014 Phys. Rev. X 4 041048
Google Scholar
[20] Ji K, Fine B V 2018 Phys. Rev. Lett. 121 050602
Google Scholar
[21] Izrailev F M 1990 Phys. Rep. 196 299
Google Scholar
[22] Zelevinsky V, Brown B A, Frazier N, Horoi M 1996 Phys. Rep. 276 85
Google Scholar
[23] Borgonovi F, Izrailev F M, Santos L F, Zelevinsky V G 2016 Phys. Rep. 626 1
Google Scholar
[24] Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126
Google Scholar
[25] Abanin D A, Altman E, Bloch I, Serbyn M 2019 Rev. Mod. Phys. 91 021001
Google Scholar
-
图 1 外磁场强度随时间做周期性变化示意图
Figure 1. Schematic plot of external magnetic field intensity with a periodic change.
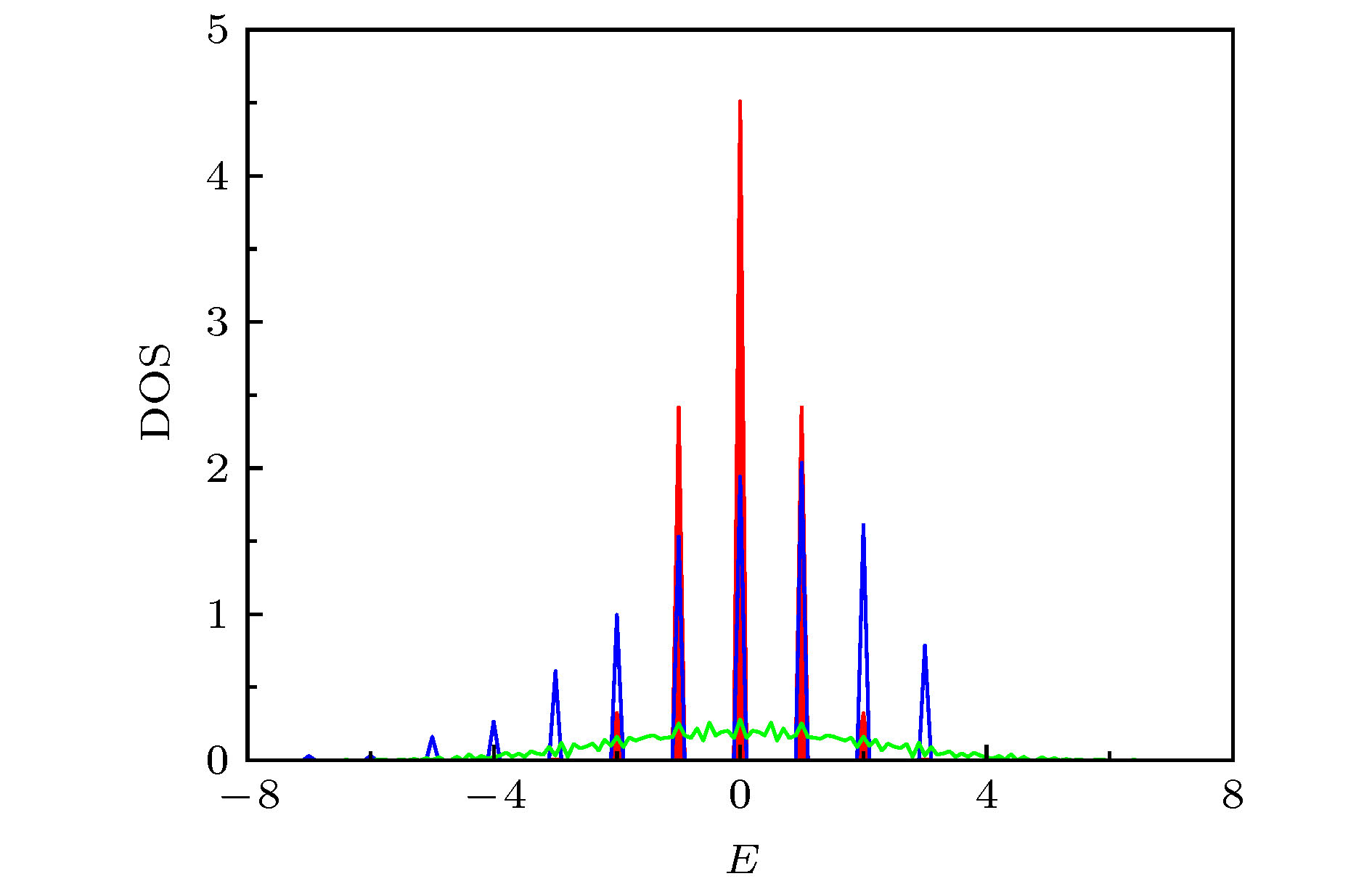
图 2 一维伊辛模型在纵向(沿
$z$ 轴)周期磁脉冲作用下本征态占据概率不发生任何变化, 其中$n$ 是磁脉冲作用的次数, 图上每一数据点代表相邻32个态的平均值, 绿线和红线分别是e指数和QMC拟合的结果Figure 2. The eigenstate occupation numbers of one-dimensional Ising model keep invariant under longitudinal periodic magnetic pulses (along the
$z$ -axis). Here$n$ is the number of magnetic pulses, each point in the graph represents the mean of 32 neighboring states, the green and red curves are the exponential and QMC fitting results, respectively.
图 3 一维伊辛模型的态密度, 其中粗红线: 无外场伊辛模型; 蓝线: 纵场伊辛模型; 细绿线: 横场伊辛模型
Figure 3. DOS of one-dimensional Ising model. Thick red curve: Ising model without external field; blue curve: Ising model with a longitudinal field; thin green curve: Ising model with a transverse field.
图 4 一维伊辛模型在横向(沿
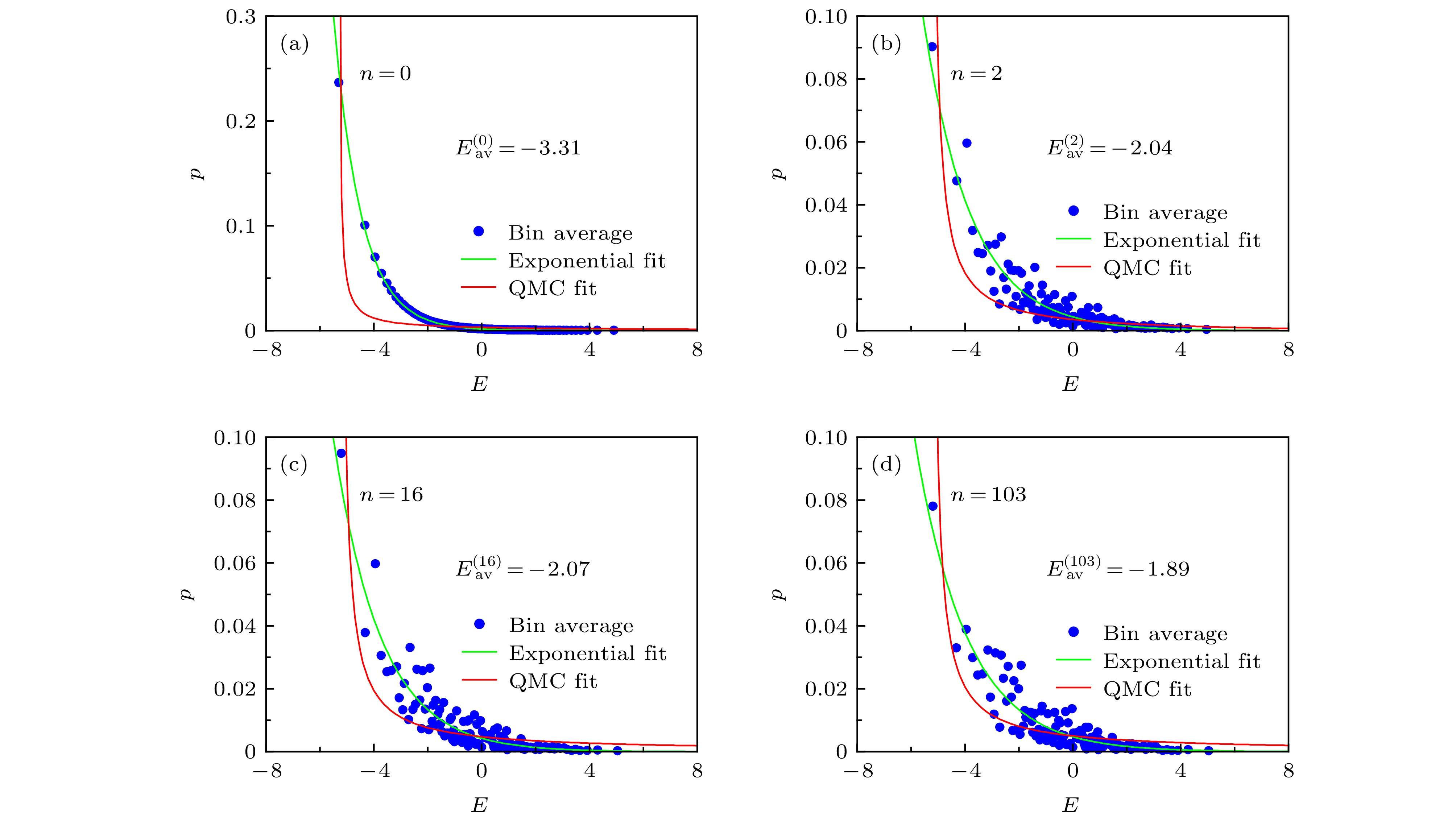
$x$ 轴)周期磁脉冲作用$n$ 次后本征态占据概率的分布 (a) n = 0; (b) n = 2; (c) n = 16; (d) n = 103. 图中每一点代表相邻32个态的平均值, 绿线和红线分别是e指数和QMC拟合的结果Figure 4. Distribution of eigenstate occupation numbers of one-dimensional Ising model after
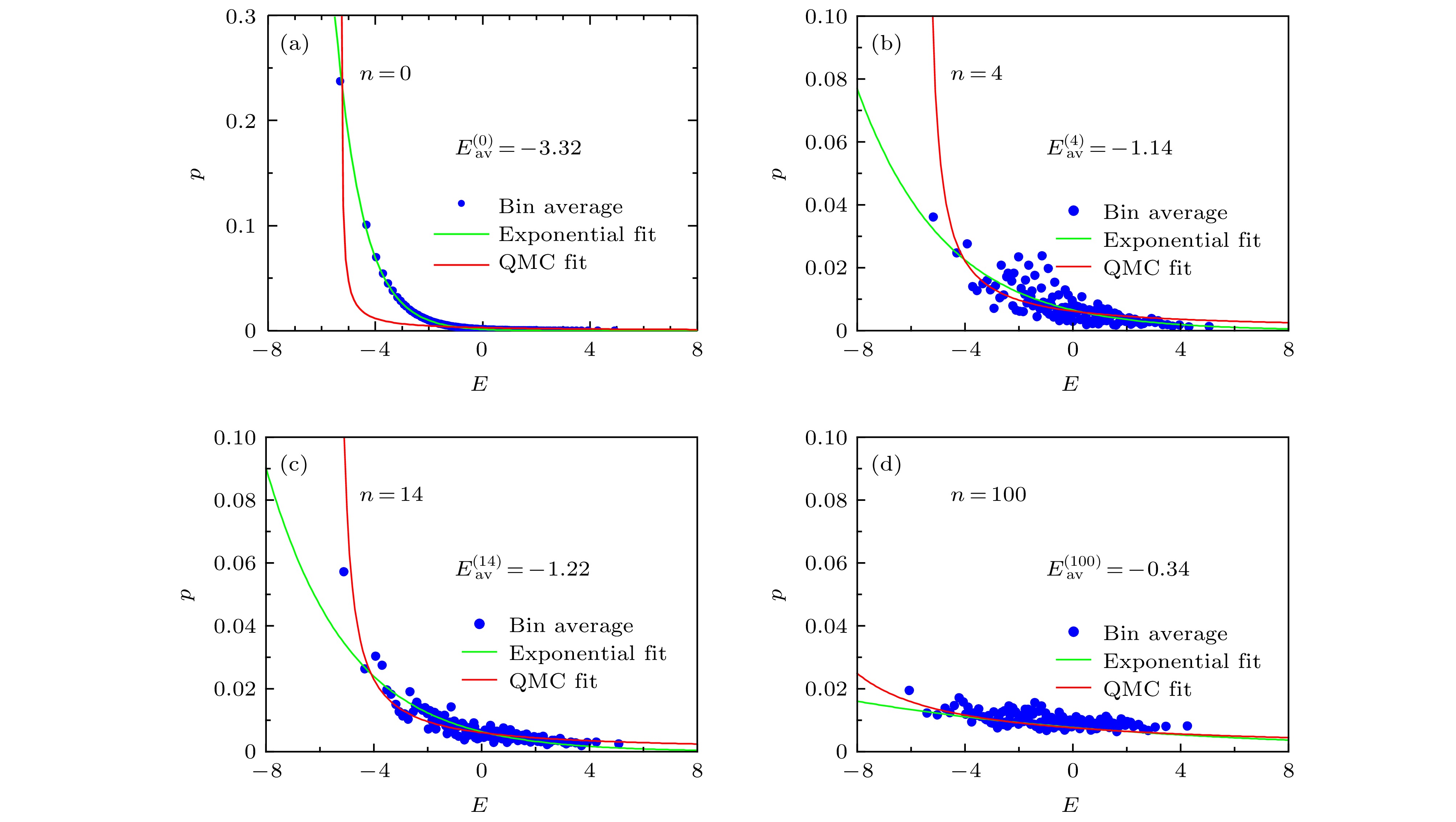
$n$ periodic transverse (along x-axis) magnetic pulses: (a) n = 0; (b) n = 2; (c) n = 16; (d) n = 103. Each point in the graph represents the mean of 32 states, the green and red curves are the exponential and QMC fitting results, respectively.
图 5 本征态占据概率分布 (a) n = 0; (b) n = 4; (c) n = 14; (d) n = 100. 与图4类似的情况, 区别是在模型中加入了微弱的随机局域磁场
Figure 5. Distribution of eigenstate occupation numbers: (a) n = 0; (b) n = 4; (c) n = 14; (d) n = 100. The situation is similar to that of Fig. 4 except for the introduction of weak random local magnetic fields.
图 6 一维伊辛模型在横向(沿
$x$ 轴)周期磁脉冲作用下弗洛凯本征态在哈密顿量${H_{{\rm{on}}}}$ 的本征态表象下的信息熵 (a) 系统不含随机局域磁场; (b) 系统包含随机局域磁场. 其中红、绿、蓝点分别对应磁脉冲的时间间隔为${t_{{\rm{off}}}} = 1, \;2, \;5$ , 黑色虚线是一维伊辛模型在纵向(沿$z$ 轴)周期磁脉冲作用下的信息熵分布Figure 6. Information entropy of the Floquet eigenstates in the eigenstate representation of
${H_{{\rm{on}}}}$ for the one-dimensional Ising model under transverse (along x-axis) periodic magnetic pulses: (a) Systems without random local magnetic fields; (b) systems with random local magnetic fields, where the red, green, and blue points correspond to magnetic pulse interval${t_{{\rm{off}}}} = 1, \;2, \;5$ , respectively, and the black dashed lines are the distribution of information entropy for the one-dimensional Ising model under longitudinal (along z-axis) periodic magnetic pulses.
图 7 一维伊辛模型在横场(沿x轴)周期磁脉冲作用下单个自旋平均能量随脉冲数n的变化 (a) 系统不含随机局域磁场; (b) 系统含随机局域磁场. 这里红方块、绿圆圈、蓝三角分别对应磁脉冲的时间间隔为
${t_{{\rm{off}}}} = 1, \;2, \;5$ , 黑色虚线是一维伊辛模型在纵向(沿z轴)周期磁脉冲作用下的单自旋平均能量Figure 7. Average energy per spin versus pulse number n for the one-dimensional Ising model under transverse (along x-axis) periodic magnetic pulses: (a) Systems without random local magnetic fields; (b) systems with random local magnetic fields, where the red squares, green circles, and blue triangles correspond to magnetic pulse interval
${t_{{\rm{off}}}} = 1, \;2, \;5$ , respectively, and the black dashed lines are the average energy per spin for the one-dimensional Ising model under longitudinal (along z-axis) periodic magnetic pulses. -
[1] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[2] Tomza M, Jachymski K, Gerritsma R, Negretti A, Calarco T, Idziaszek Z, Julienne P S 2019 Rev. Mod. Phys. 91 035001
Google Scholar
[3] Shi F, Kong X, Wang P, Kong F, Zhao N, Liu R B, Du J 2014 Nat. Phys. 10 21
Google Scholar
[4] Gao W B, Imamoglu A, Bernien H, Hanson R 2015 Nat. Photonics 9 363
Google Scholar
[5] Huang K 1987 Statistical Mechanics (New York: Wiley) pp131–135
[6] Pathria R K, Beale P D 2011 Statistical Mechanics (3rd Ed.) (Boston: Academic) pp115–119
[7] Popescu S, Short A J, Winter A 2006 Nat. Phys. 2 754
Google Scholar
[8] Goldstein S, Lebowitz J L, Tumulka R, Zanghì N 2006 Phys. Rev. Lett. 96 050403
Google Scholar
[9] Reimann P 2007 Phys. Rev. Lett. 99 160404
Google Scholar
[10] Mahler G, Gemmer J, Michel M 2005 Physica E 29, 53
Google Scholar
[11] Levine R D 1988 J. Stat. Phys. 52 1203
Google Scholar
[12] Buch V, Gerber R B, Ratner M A 1982 J. Chem. Phys. 76 5397
Google Scholar
[13] Brody D C, Hughston L P 1998 J. Math. Phys. 39 6502
Google Scholar
[14] Bender C M, Brody D C, Hook D W 2005 J. Phys. A: Math. Gen. 38 L607
Google Scholar
[15] Naudts J, Van der Straeten E 2006 J. Stat. Mech.: Theory Exp. 2006 06015
Google Scholar
[16] Fine B V 2009 Phys. Rev. E 80 051130
Google Scholar
[17] Campisi M 2013 New J. Phys. 15 115008
Google Scholar
[18] Ji K, Fine B V 2011 Phys. Rev. Lett. 107 050401
Google Scholar
[19] D'Alessio L, Rigol M 2014 Phys. Rev. X 4 041048
Google Scholar
[20] Ji K, Fine B V 2018 Phys. Rev. Lett. 121 050602
Google Scholar
[21] Izrailev F M 1990 Phys. Rep. 196 299
Google Scholar
[22] Zelevinsky V, Brown B A, Frazier N, Horoi M 1996 Phys. Rep. 276 85
Google Scholar
[23] Borgonovi F, Izrailev F M, Santos L F, Zelevinsky V G 2016 Phys. Rep. 626 1
Google Scholar
[24] Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126
Google Scholar
[25] Abanin D A, Altman E, Bloch I, Serbyn M 2019 Rev. Mod. Phys. 91 021001
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6626
- PDF Downloads: 76
- Cited By: 0
