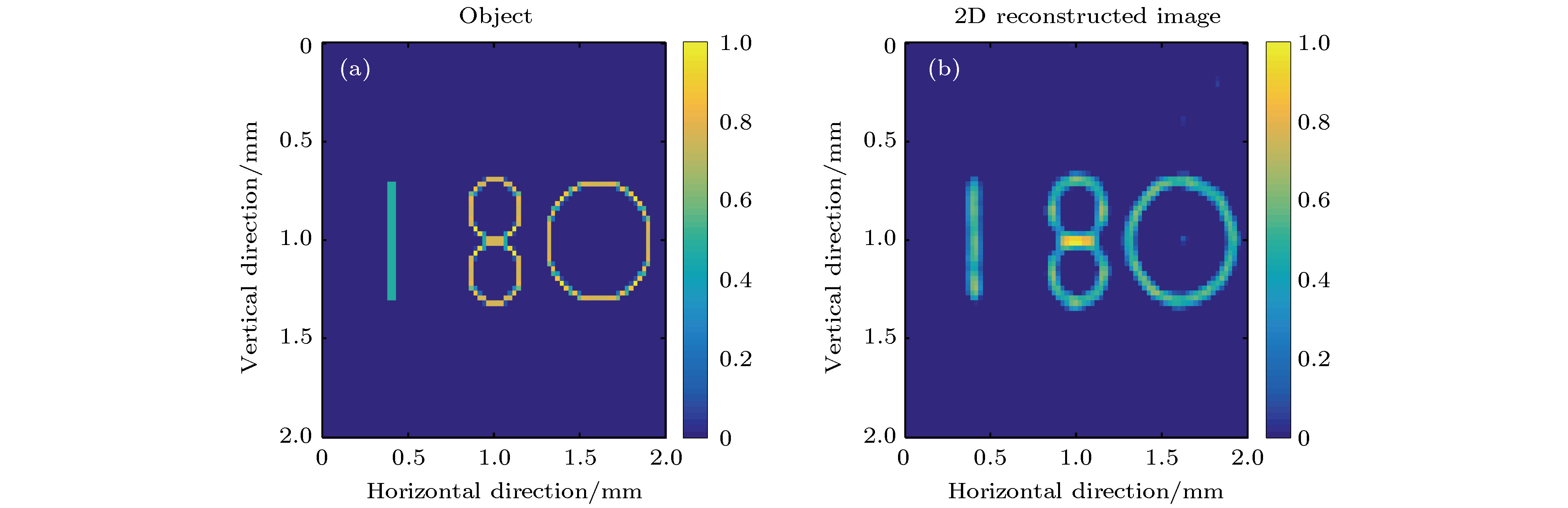
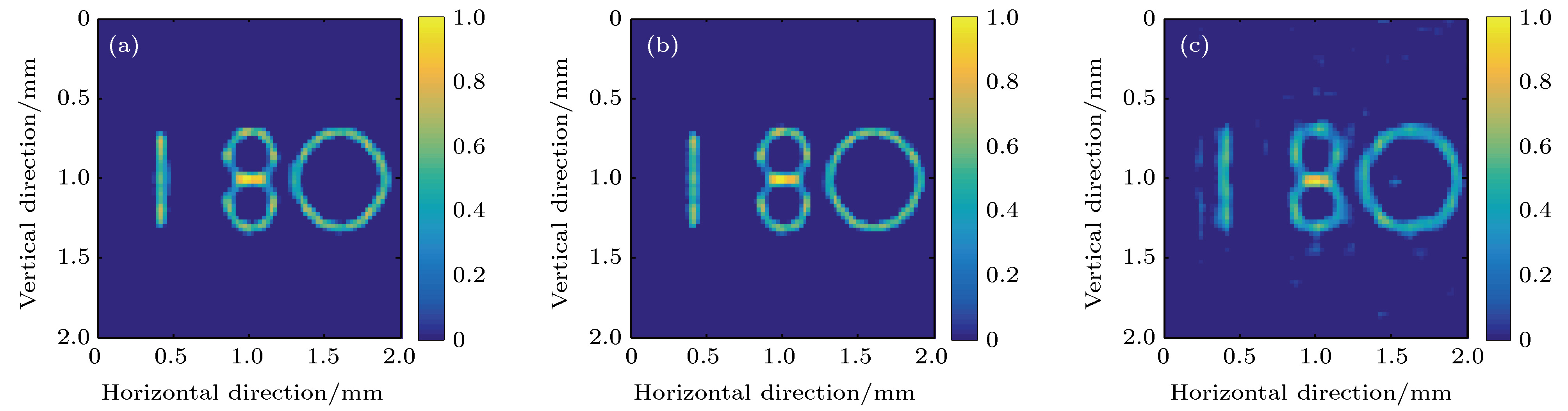
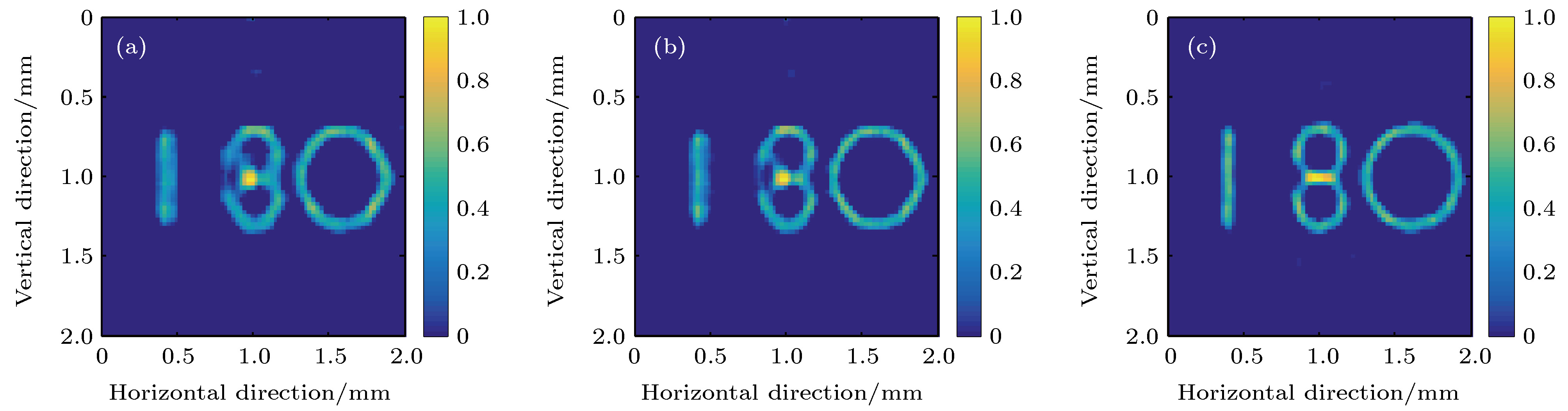
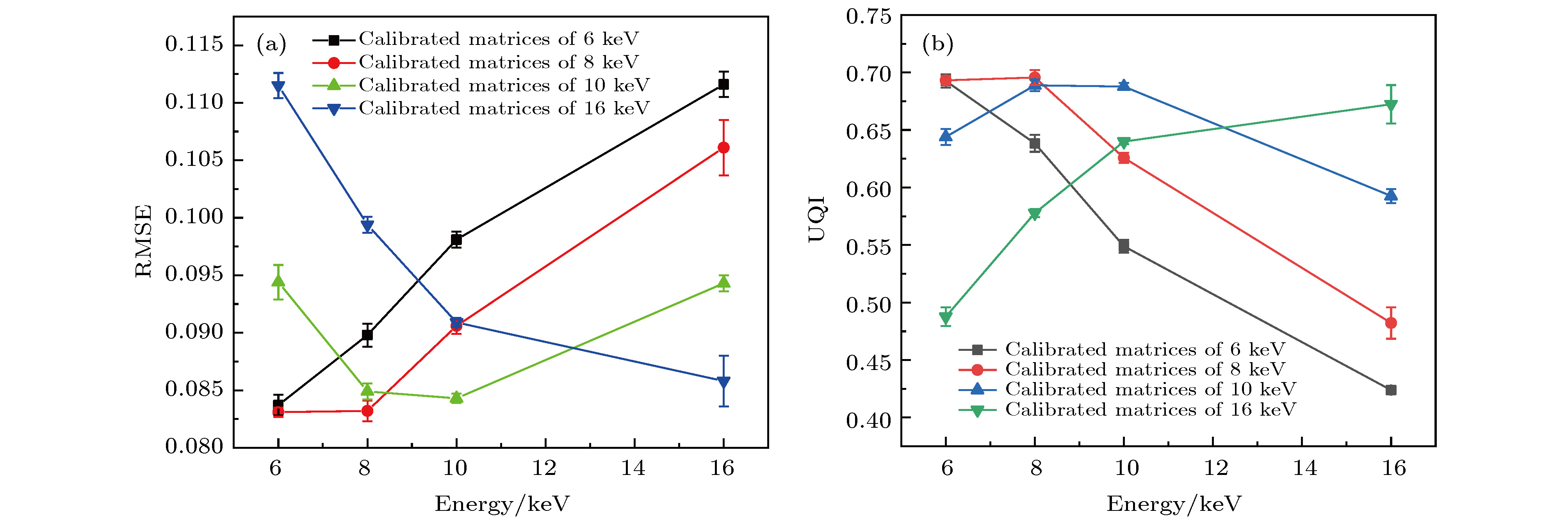
-
Compared with traditional X-ray imaging systems based on polycapillary X-ray optics or a pinhole, coded aperture imaging system has the advantages in simple structure, high sensitivity, and strong expandability, which make it possess the potential applications in X-ray fluorescence imaging. In this work, a new coded aperture X-ray imaging system based on a novel imaging model which decomposes the mask projections into a superposition of two separable functions is designed and proposed for high-resolution X-ray imaging. The performance of the system is demonstrated by using the Geant4 package. To reduce the computational complexity of calibration and image reconstruction, a separable mask with 90 × 90 pixels is used. The mask is designed by selecting the central part of the original rank 463 modified uniformly redundant arrays. The mask is made of platinum foil with a pixel pitch of 25 microns. To study the effect of mask thickness on system performance, the mask thickness is varied from 25 to 200 microns. The active area of the Si detector employed in the system is 2 mm × 2 mm, divided into 80 × 80 pixels, each with a size of 25 μm × 25 μm. The field of view of the system is equal to the area of the detector, which is 2 mm × 2 mm. The detector is parallel to and center-aligned with the mask with a fixed distance of 2.0 mm. The images are reconstructed by using the fast iterative shrinkage-thresholding algorithm. The high-quality reconstructed images of different energy line sources and complex shaped objects are obtained. The simulation and analysis results indicate that for the near-field imaging, unlike imaging systems based on the conventional convolution model, the system has the performance that is not affected by the aperture collimation effect. The spatial resolution of the imaging system is about 65 microns. The calibrated matrices used have an important influence on the image quality. The quality of the reconstructed image is affected by the energy of X-rays used during calibration and the energy of X-rays emitted from the object; the smaller the difference between these two energy values, the higher the quality of the reconstructed images will be. The three-dimensional reconstruction results show that the system can correctly estimate the distance between the object and the system from a single two-dimensional projection. The axial spatial resolution of the system is about 1.1 mm.
-
Keywords:
- coded aperture /
- X-ray fluorescence imaging /
- Monte Carlo simulation /
- image reconstruction
[1] Terzano R, Denecke M A, Falkenberg G, Miller B, Paterson D, Janssens K 2019 Pure Appl. Chem. 91 1029
Google Scholar
[2] Romano F P, Caliri C, Cosentino L, Gammino S, Giuntini L, Mascali D, Neri L, Pappalardo L, Rizzo F, Taccetti F 2014 Anal. Chem. 86 10892
Google Scholar
[3] Tsuji K, Matsuno T, Takimoto Y, Yamanashi M, Kometani N, Sasaki Y C, Hasegawa T, Kato S, Yamada T, Shoji T, Kawahara N 2015 Spectrom. Acta B 113 43
Google Scholar
[4] Buzanich G, Radtke M, Reinholz U, Riesemeier H, Thünemann A F, Streli C 2012 J. Anal. At. Spectrom. 27 1875
Google Scholar
[5] Rauwolf M, Turyanskaya A, Roschger A, Prost J, Simon R, Scharf O, Radtke M, Schoonjans T, Buzanich A G, Klaushofer K, Wobrauschek P, Hofstaetter J G, Roschger P, Streli C 2017 J. Synchrotron Radiat. 24 307
Google Scholar
[6] Zhang H, Jiang S W, Liao J, Deng J J, Liu J, Zhang Y B, Zheng G A 2019 Opt. Express 27 7498
Google Scholar
[7] 强鹏飞, 盛立志, 李林森, 闫永清, 刘哲, 周晓红 2019 物理学报 68 160702
Google Scholar
Qiang P F, Sheng L Z, Li L S, Yan Y Q, Liu Z, Zhou X H 2019 Acta Phys. Sin. 68 160702
Google Scholar
[8] Dicke R H 1968 Astrophys. J. 153 L101
Google Scholar
[9] Ables J G 1968 Astron. Soc. Aust. 1 172
Google Scholar
[10] Cieślak M J, Gamage K A A, Glover R 2016 Radiat. Meas. 92 59
Google Scholar
[11] Liu Y T, Xiao X, Zhang Z M, Wei L 2020 Nucl. Instrum. Methods Phys. Res. A 957 163385
Google Scholar
[12] Sun S F, Liu Y, Ouyang X P 2020 Radiat. Phys. Chem. 174 108891
Google Scholar
[13] Haboub A, MacDowell A A, Marchesini S, Parkinson D Y 2014 Rev. Sci. Instrum. 85 063704
Google Scholar
[14] Kulow A, Buzanich A G, Reinholz U, Streli C, Radtke M 2020 J. Anal. At. Spectrom. 35 347
Google Scholar
[15] DeWeert M J, Farm B P 2015 Opt. Eng. 54 023102
Google Scholar
[16] Asif M S, Ayremlou A, Sankaranarayanan A, Veeraraghavan A, Baraniuk R G 2017 IEEE Trans. Comput. Imaging 3 384
Google Scholar
[17] Adams J K, Boominathan V, Avants B W, Vercosa D G, Ye F, Baraniuk R G, Robinson J T, Veeraraghavan A 2017 Sci. Adv. 3 e1701548
Google Scholar
[18] Sun S F, Liu Y, Ouyang X P 2020 Nucl. Instrum. Methods Phys. Res. A 951 163001
Google Scholar
[19] Beck A, Teboulle M 2009 SIAM J. Imaging Sci. 2 183
Google Scholar
[20] Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, Bagli E, Bagulya A, Banerjee S, Barrand G 2016 Nucl. Instrum. Methods Phys. Res. A 835 186
Google Scholar
[21] Wang Z, Bovik A C 2002 IEEE Signal Process. Lett. 9 81
Google Scholar
-
图 1 编码孔径成像示意图
Figure 1. Schematics diagram of coded aperture imaging
图 2 模拟选用的可编码准直器图样
Figure 2. The mask pattern used in the simulation.
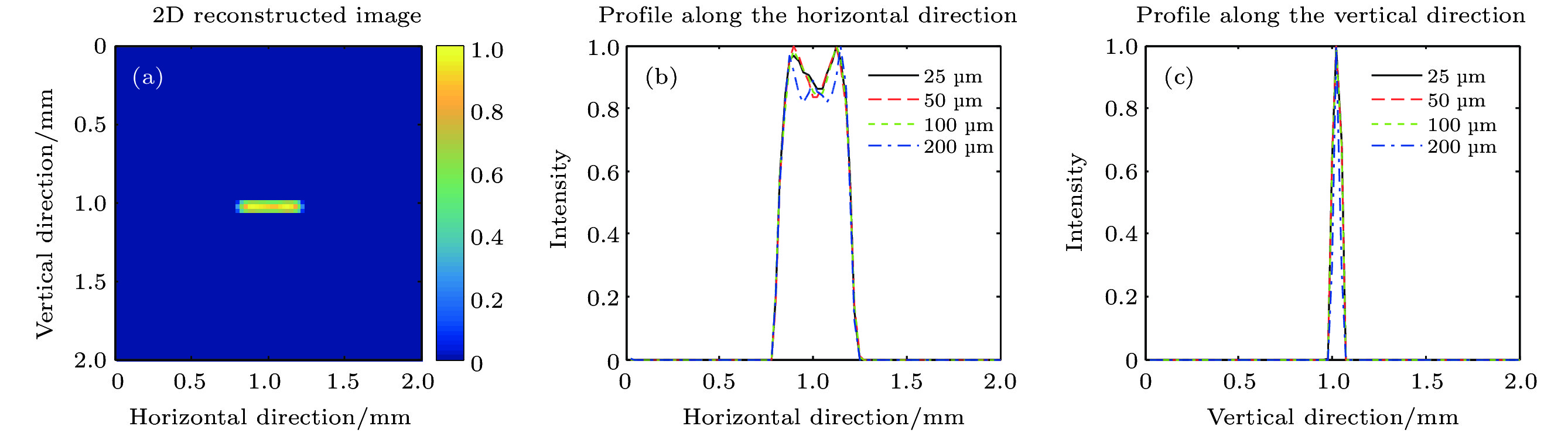
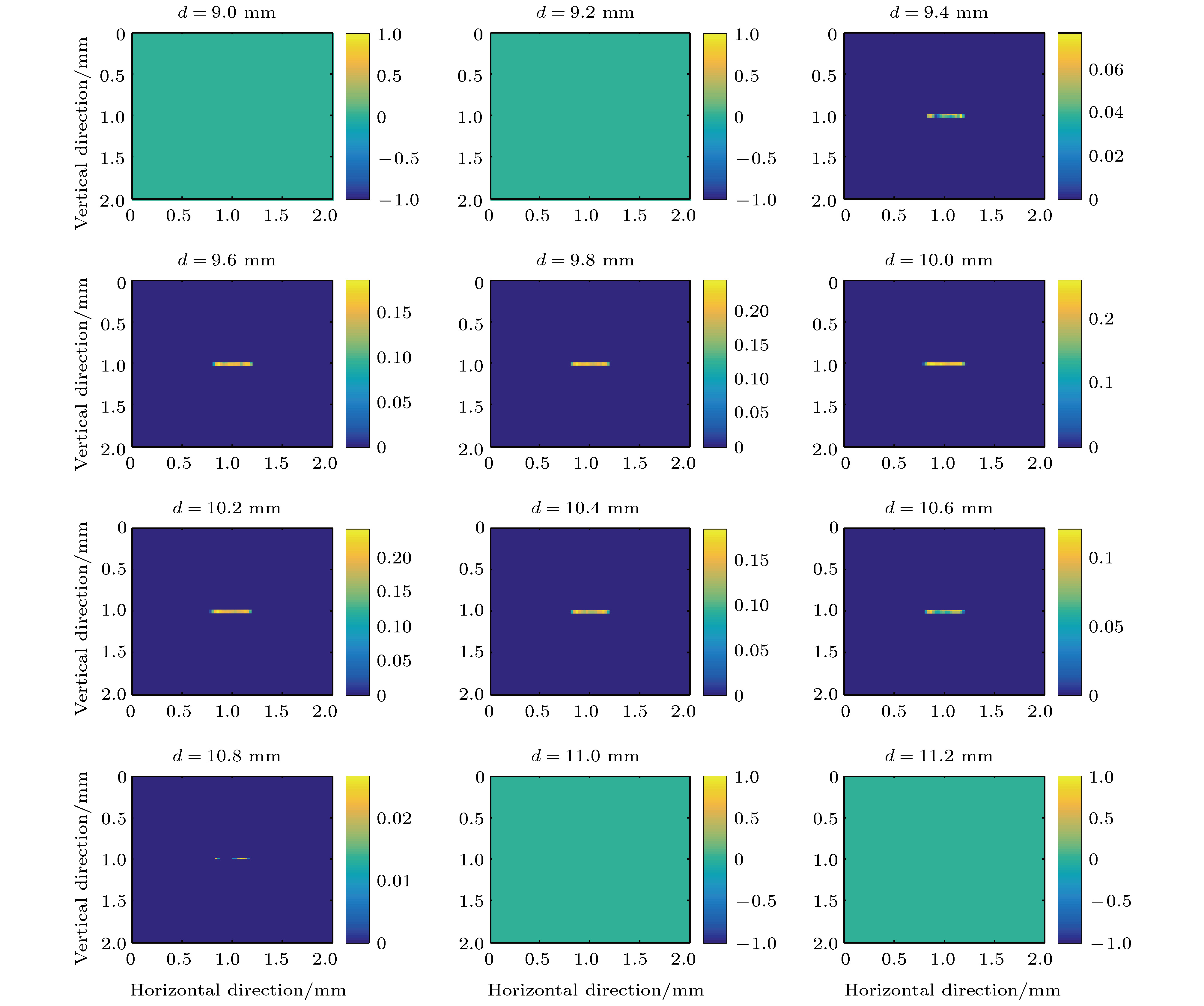
图 3 线源二维重建图像及其沿横纵向分布 (a)准直器厚度25微米时的线源重建图像; (b)不同准直器厚度时的横向分布; (c)不同准直器厚度时的纵向分布
Figure 3. 2 d reconstructed image of the line source and its horizontal and vertical distribution: (a) Reconstructed image of the line source when the mask thickness was 25 micron; (b) horizontal distribution for different mask thickness; (c) vertical distribution for different mask thickness.
图 4 物体的原始图像及重建图像 (a)原始图像; (b)准直器厚度25微米时的重建图像
Figure 4. Original image and reconstructed image of the object: (a) Original image; (b) reconstructed image when the mask thickness was 25 micron.
图 5 校准能量10 keV情况下物体不同能量时的重建图像 (a) 6 keV; (b) 8 keV; (c) 16 keV
Figure 5. Reconstructed images of the object with different energies at a calibration energy of 10 keV: (a) 6 keV; (b) 8 keV; (c) 16 keV.
图 6 校准能量16 keV情况下物体不同能量时的重建图像 (a) 6 keV; (b) 8 keV; (c) 16 keV
Figure 6. Reconstructed images of the object with different energies at a calibration energy of 16 keV: (a) 6 keV; (b) 8 keV; (c) 16 keV.
图 7 重建图像质量的定量评价结果随物体能量和校准能量的变化情况 (a) RMSE; (b) UQI
Figure 7. Quantitative evaluation results of reconstructed images change with the object energy and calibration energy: (a) RMSE; (b) UQI
图 8 线源的三维重建图像
Figure 8. 3D reconstructed image of the line source.
图 9 复杂物体的三维重建图像
Figure 9. 3D reconstructed image of the complex object.
-
[1] Terzano R, Denecke M A, Falkenberg G, Miller B, Paterson D, Janssens K 2019 Pure Appl. Chem. 91 1029
Google Scholar
[2] Romano F P, Caliri C, Cosentino L, Gammino S, Giuntini L, Mascali D, Neri L, Pappalardo L, Rizzo F, Taccetti F 2014 Anal. Chem. 86 10892
Google Scholar
[3] Tsuji K, Matsuno T, Takimoto Y, Yamanashi M, Kometani N, Sasaki Y C, Hasegawa T, Kato S, Yamada T, Shoji T, Kawahara N 2015 Spectrom. Acta B 113 43
Google Scholar
[4] Buzanich G, Radtke M, Reinholz U, Riesemeier H, Thünemann A F, Streli C 2012 J. Anal. At. Spectrom. 27 1875
Google Scholar
[5] Rauwolf M, Turyanskaya A, Roschger A, Prost J, Simon R, Scharf O, Radtke M, Schoonjans T, Buzanich A G, Klaushofer K, Wobrauschek P, Hofstaetter J G, Roschger P, Streli C 2017 J. Synchrotron Radiat. 24 307
Google Scholar
[6] Zhang H, Jiang S W, Liao J, Deng J J, Liu J, Zhang Y B, Zheng G A 2019 Opt. Express 27 7498
Google Scholar
[7] 强鹏飞, 盛立志, 李林森, 闫永清, 刘哲, 周晓红 2019 物理学报 68 160702
Google Scholar
Qiang P F, Sheng L Z, Li L S, Yan Y Q, Liu Z, Zhou X H 2019 Acta Phys. Sin. 68 160702
Google Scholar
[8] Dicke R H 1968 Astrophys. J. 153 L101
Google Scholar
[9] Ables J G 1968 Astron. Soc. Aust. 1 172
Google Scholar
[10] Cieślak M J, Gamage K A A, Glover R 2016 Radiat. Meas. 92 59
Google Scholar
[11] Liu Y T, Xiao X, Zhang Z M, Wei L 2020 Nucl. Instrum. Methods Phys. Res. A 957 163385
Google Scholar
[12] Sun S F, Liu Y, Ouyang X P 2020 Radiat. Phys. Chem. 174 108891
Google Scholar
[13] Haboub A, MacDowell A A, Marchesini S, Parkinson D Y 2014 Rev. Sci. Instrum. 85 063704
Google Scholar
[14] Kulow A, Buzanich A G, Reinholz U, Streli C, Radtke M 2020 J. Anal. At. Spectrom. 35 347
Google Scholar
[15] DeWeert M J, Farm B P 2015 Opt. Eng. 54 023102
Google Scholar
[16] Asif M S, Ayremlou A, Sankaranarayanan A, Veeraraghavan A, Baraniuk R G 2017 IEEE Trans. Comput. Imaging 3 384
Google Scholar
[17] Adams J K, Boominathan V, Avants B W, Vercosa D G, Ye F, Baraniuk R G, Robinson J T, Veeraraghavan A 2017 Sci. Adv. 3 e1701548
Google Scholar
[18] Sun S F, Liu Y, Ouyang X P 2020 Nucl. Instrum. Methods Phys. Res. A 951 163001
Google Scholar
[19] Beck A, Teboulle M 2009 SIAM J. Imaging Sci. 2 183
Google Scholar
[20] Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, Bagli E, Bagulya A, Banerjee S, Barrand G 2016 Nucl. Instrum. Methods Phys. Res. A 835 186
Google Scholar
[21] Wang Z, Bovik A C 2002 IEEE Signal Process. Lett. 9 81
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6826
- PDF Downloads: 126
- Cited By: 0
