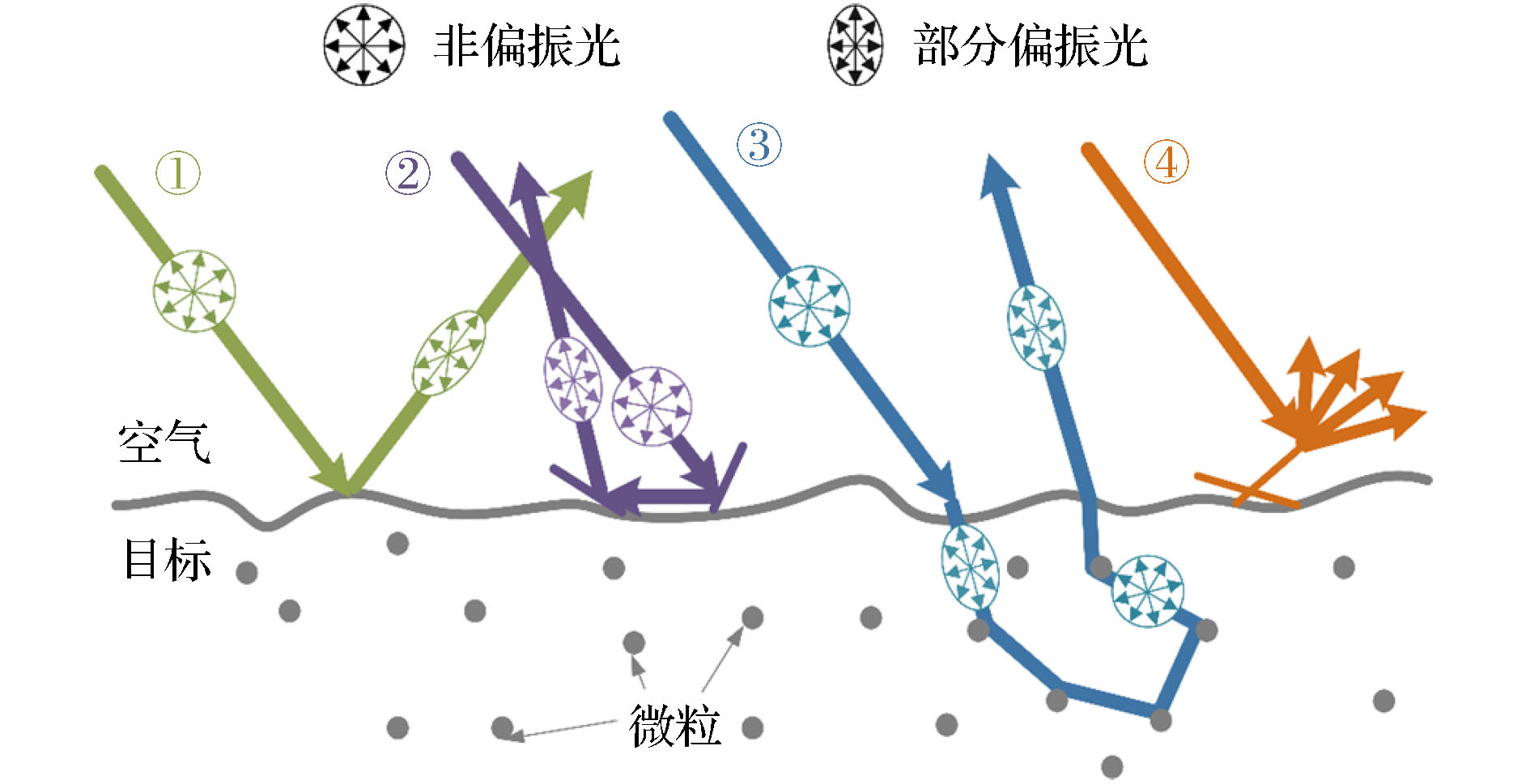
-
The reflection light field of surface of the Non-Lambertian body in nature has both specular reflection and diffuse reflection components. In the process of three-dimensional(3D) reconstruction, image matching and pattern recognition are based on the ideal Lambert body. The imaging effect is limited due to the presence of specular reflection components, and the accuracy of feature recognition is low. In order to obtain the diffuse reflection component accurately, a large number of studies have been conducted for a long time, which can be mainly divided into two parts: intensity- and polarization-based separation techniques. The intensity-based separation algorithm is limited in many aspects due to the prior knowledge, such as light source chromaticity, direction and image color information. With the maturity of detection technology, the acquisition and interpretation of multi-dimensional physical properties of light-field have made great progress of the utilization of polarization characteristics of light wave. Compared with traditional intensity imaging technology, the polarization imaging technology has strongr and many advantages in highlighting targets. However, in traditional polarization-based separation techniques, it is often necessary to assume that the diffuse light is completely unpolarized, which is used in some specific cases but not universally. In this work, we report a method to obtain the diffuse reflection components of the target surface based on the polarization characteristics of the light-field. According to Fresnel's law and Lawrence B. Wolff's reflection model, the reflected light-field on the target surface can be divided into diffuse and specular components with partial polarization. The partial polarization characteristics of diffuse and specular components are explored in depth and the Stokes vector is used to calculate the minimum light intensity of each pixel modulated by polarizer, which is completely unpolarized light. By subtracting completely unpolarized light from the obtained polarized sub-images, the diffuse and specular components in the polarized part satisfy the linear constraint model. Based on the independent component analysis (ICA) model, the diffuse and specular components in the polarized part are regarded as independent and non-interfering additive vectors. The singular value decomposition method and optical relevancy of mutual information are used to determine the optimal mix coefficients matrix of the subcomponents in the linear constrained model. Thus, the diffuse components are accurately acquired and explained from the complex reflected light-field. Simulation and experimental results show that the algorithm mentioned above can accurately obtain the optimal mix coefficients’ matrix without the prior knowledge of illuminant chromaticity, or direction or image chromatic information, or others. This technique can accurately obtain and remove the specular reflection part, at the same time, restore the diffuse light intensity which is covered by the specular reflection and conforms to the change trend of the surface shape. Meanwhile, the pretty good results also demonstrate that the proposed separation method has the strong stability and wide applicability. This technology does not have to make the assumption that 3D imaging technology and computer vision algorithms such as pattern recognition rely on natural objects as ideal Lambert bodies, and it can eleminate the influence of complex reflected light-field on target results, which makes passive remote 3D imaging technology more applicable and more robust. [1] Zhang W Z, Chen Z B, Xia B F, Lin B, Cao X Q 2014 Chin. Phys. B 23 044212
Google Scholar
[2] Salvi J, Pages J, Batlle J 2004 Pattern Recognit. 37 827
Google Scholar
[3] Varady T, Martin R R, Cox J 1997 Comput.-Aided Des. 29 255
Google Scholar
[4] 周光照, 王玉丹, 任玉琦, 陈灿, 叶琳琳, 肖体乔 2012 物理学报 61 018701
Google Scholar
Zhou G Z, Wang Y D, Ren Y Q, Chen C, Ye L L, Xiao T Q 2012 Acta Phys. Sin. 61 018701
Google Scholar
[5] Zhang R, Tsai P S, Cryer J E, Shah M 1999 IEEE Trans. Pattern Anal. Mach. Intell. 21 690
Google Scholar
[6] Jiang L, Zhang J Y, Deng B L, Li H, Liu L G 2018 IEEE Trans. Image Process. 27 4756
Google Scholar
[7] Shafer S A 1985 Color Res. Appl. 10 210
Google Scholar
[8] Klinker G J, Shafer S A, Kanade T 1988 Int. J. Comput. Vision 2 7
Google Scholar
[9] Klinker G J, Shafer S A, Kanade T 1990 Int. J. Comput. Vision 4 7
Google Scholar
[10] Novak C L, Shafer S A 1992 Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Champaign, USA, June 15–18, 1992 p599
[11] Tan P, Quan L, Lin S 2006 Proceedings 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition New York, USA, June 17–22, 2006 p1855
[12] Shen H L, Zheng Z H 2013 Appl. Opt. 52 4483
Google Scholar
[13] Ren W H, Tian J D, Tang Y D 2017 IEEE Trans. Image Process. 26 2327
Google Scholar
[14] Sato Y, Ikeuchi K 1994 J. Opt. Soc. Am. A: 11 2990
Google Scholar
[15] Wolff L B, Boult T E 1991 IEEE Trans. Pattern Anal. Mach. Intell. 13 635
Google Scholar
[16] Nayar S K, Fang X S, Boult T 1997 Int. J. Comput. Vision 21 163
Google Scholar
[17] Umeyama S J, Godin G 2004 IEEE Trans. Pattern Anal. Mach. Intell. 26 639
Google Scholar
[18] Atkinson G A, Hancock E R 2007 IEEE Trans. Pattern Anal. Mach. Intell. 29 2001
Google Scholar
[19] 王文波, 张晓东, 汪祥莉 2013 物理学报 62 050201
Google Scholar
Wang W B, Zhang X D, Wang X L 2013 Acta Phys. Sin. 62 050201
Google Scholar
[20] Comon P 1994 Signal Process. 36 287
Google Scholar
[21] TichavskÝ P, Kybernetika Z 2011 Kybernetika 47 426
[22] Hyvarinen A, Oja E 2000 Neural Networks 13 411
Google Scholar
[23] Adachi K, Trendafilov N T 2018 Psychometrika 83 407
Google Scholar
[24] Li Z, Liu D T, Ye T, Chen G H, Zhang L H, Yang Q S, Ji F 2007 Chin. Phys. Lett. 16 2913
Google Scholar
[25] Biglieri E, Yao K 1989 Signal Process. 18 277
Google Scholar
[26] 赵辽英, 吕步云, 厉小润, 陈淑涵 2015 物理学报 64 124204
Google Scholar
Zhao L Y, Lü B Y, Li X R, Chen S H 2015 Acta Phys.Sin. 64 124204
Google Scholar
-
图 1 物体表面反射光分类
Figure 1. Classification of reflected light on the reflection surface.
图 2 (a) 仿真人脸深度信息; (b), (c) 通过渲染后的漫反射和镜面反射仿真图像
Figure 2. (a) Simulated face depth information; (b), (c) simulated images with diffuse and specular reflections after rendering, respectively.
图 3 基于二色反射模型的四幅模拟图像 (a), (b), (c), (d)分别代表(8)式混合后的光强分布
$I_1^{\rm{Total}}$ ,$I_2^{\rm{Total}}$ ,$I_3^{\rm{Total}}$ 和$I_4^{\rm{Total}}$ Figure 3. Four simulated images based on dichromatic reflection model, (a), (b), (c) and (d) represent the intensity image
$I_1^{\rm{Total}}$ ,$I_1^{\rm{Total}}$ ,$I_3^{\rm{Total}}$ and$I_4^{\rm{Total}}$ obtained from Eq. (8), respectively.
图 4 互信息随β变化情况及镜面反射和漫反射最终分离结果 (a) 分离的最优漫反射; (b) 分离的最优镜面反射
Figure 4. Mutual information variation and the finally separated diffuse and specular reflection: (a) The optimal separated diffuse reflection; (b) the optimal separated specular reflection.
图 5 10组仿真测试数据图 Coef1, Coef2, Coef3和Coef4是镜面反射分量混合系数的4个设定值; Coef1-Ours, Coef2-Ours, Coef3-Ours和Coef4-Ours是算法得到的混合系数值; Eu-Dis表示每组设定值组成的向量跟算法计算值组成的向量之间的欧氏距离
Figure 5. Plots of ten sets of simulation test data: Coef1, Coef2, Coef3 and Coef4 are four set values of the coefficients of the specular reflection components; Coef1-Ours, Coef2-Ours, Coef3-Ours and Coef4-Ours are the coefficients obtained by our algorithm; Eu-Dis represents the Euclidean distance between the vector composed of set values and the vector composed of the calculated values of our algorithm in each group.
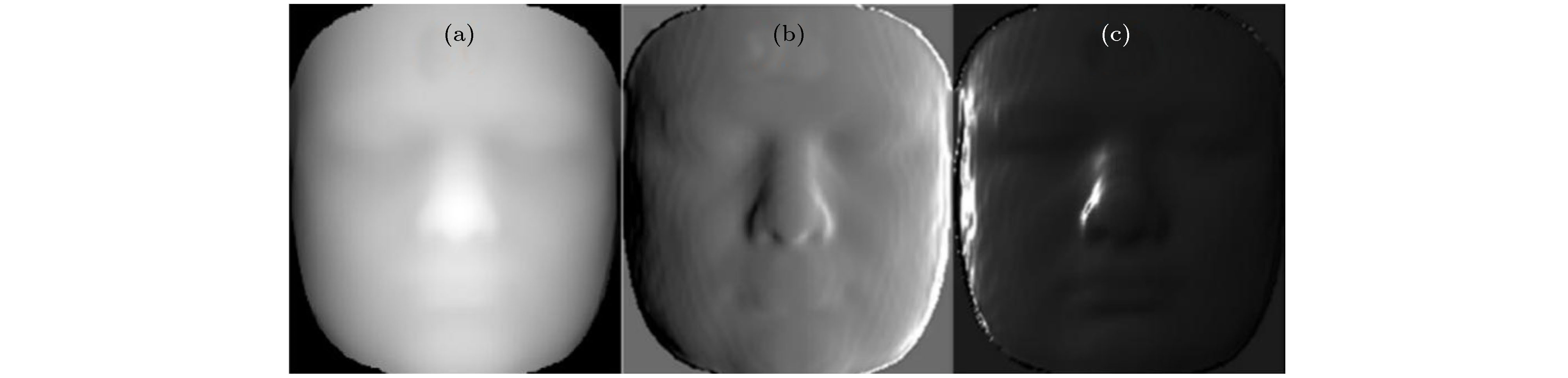
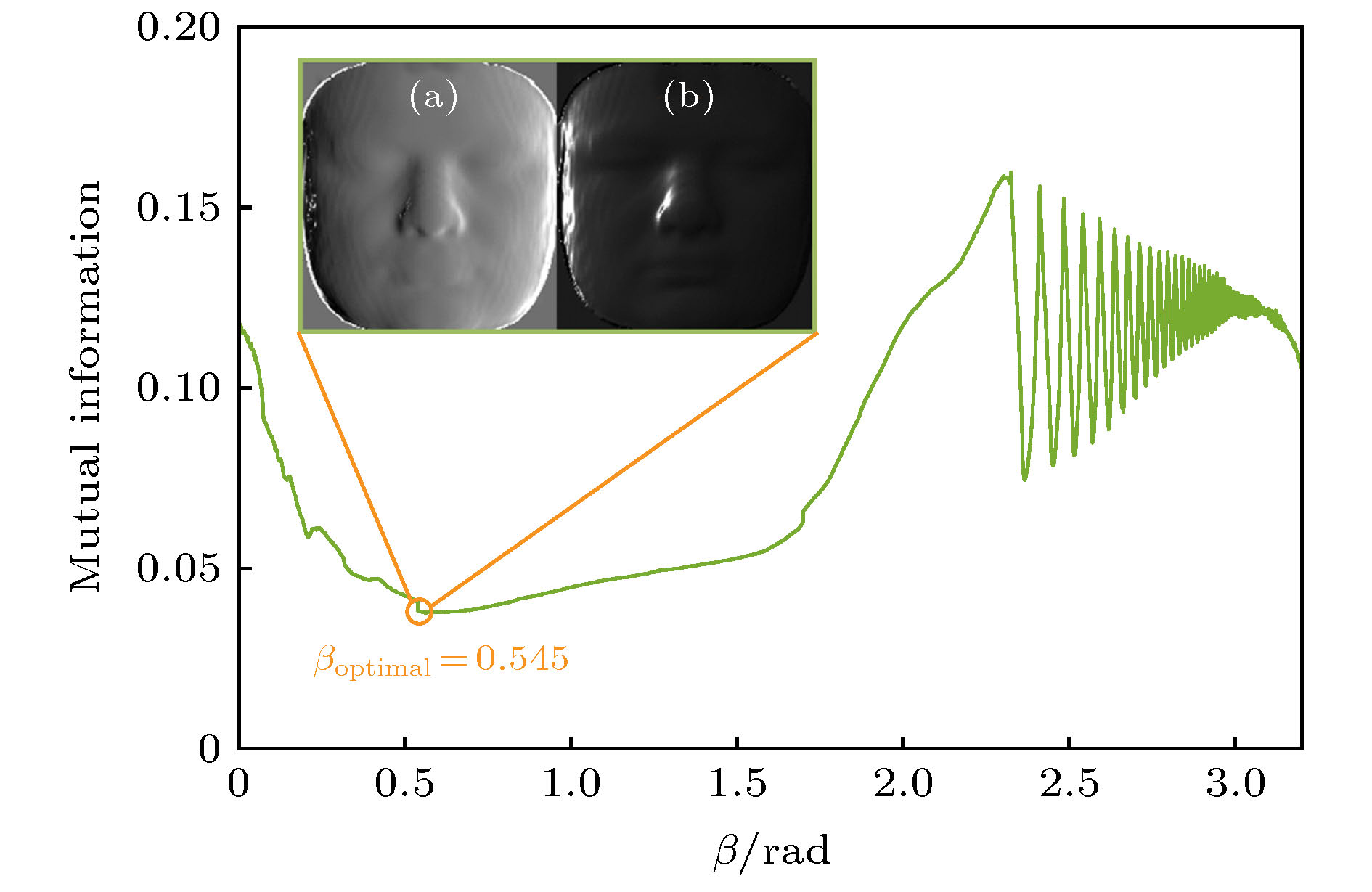
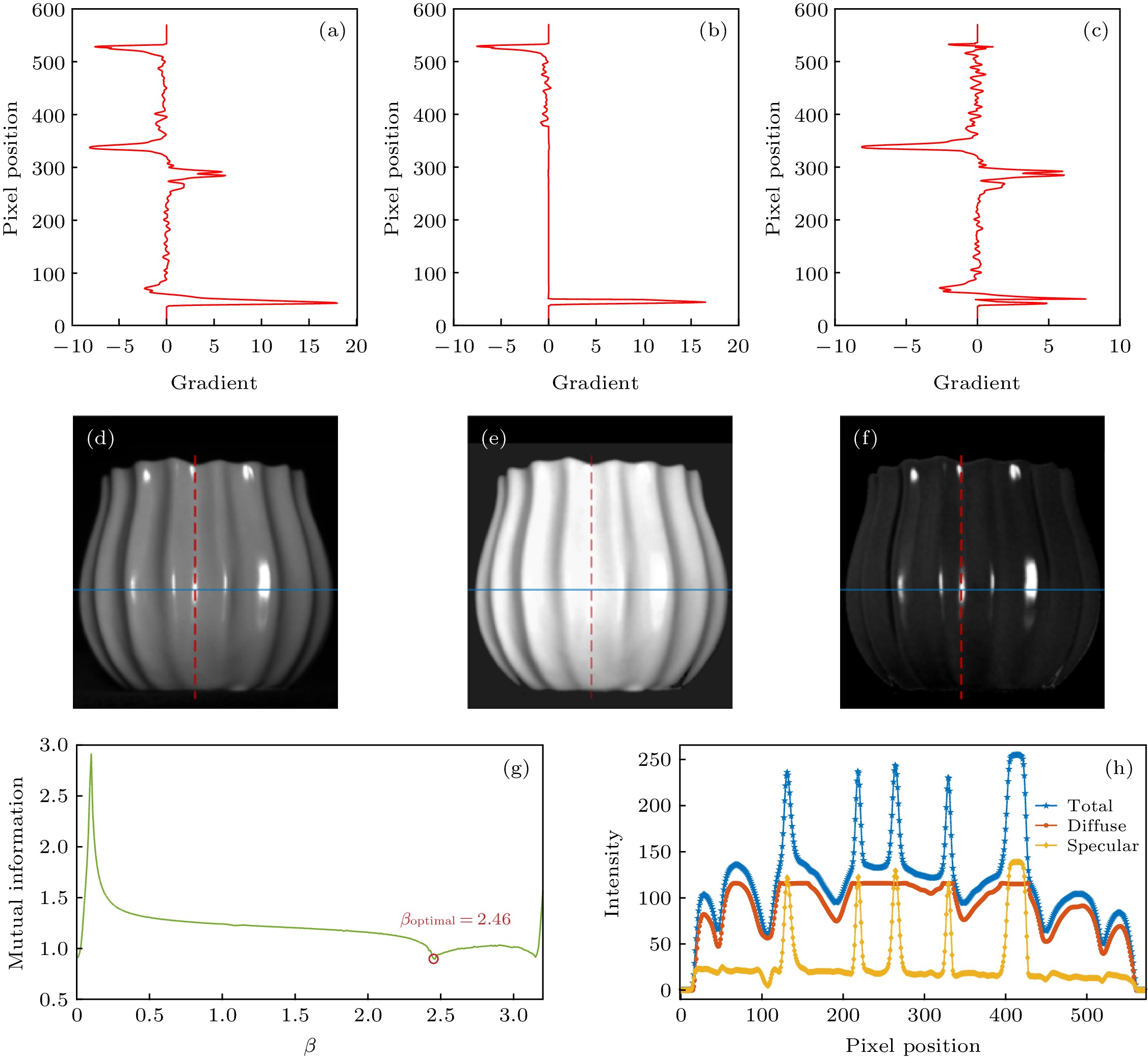
图 6 陶瓷目标表面反射光强分布及分离结果 (a), (b)和(c)分别为图(d), (e)和(f)沿图示红虚线处的光强梯度分布; (d)是偏振片在0°方向下获取的目标原始光强图片; (e)和(f)分别是算法处理后最优的漫反射和镜面反射光强分布; (g)是算法处理过程中得到的互信息图; (h)是(d), (e), (f)沿图示蓝实线位置的光强截面结果
Figure 6. Intensity distribution and separation results on the surface of ceramic object: (a), (b) and (c) are the light intensity gradient distribution along the red dotted line shown in Fig. (d), (e) and (f), respectively; (d) is the original light intensity of the target obtained from the polarizer at the direction of 0°; (e) and (f) are the optimal light intensity distributions of diffuse and specular component after our algorithm, respectively; (g) is the mutual information plot obtained during algorithm processing; (h) is the results of light intensity cross section obtained along the blue solid line in Fig. (d), (e) and (f).
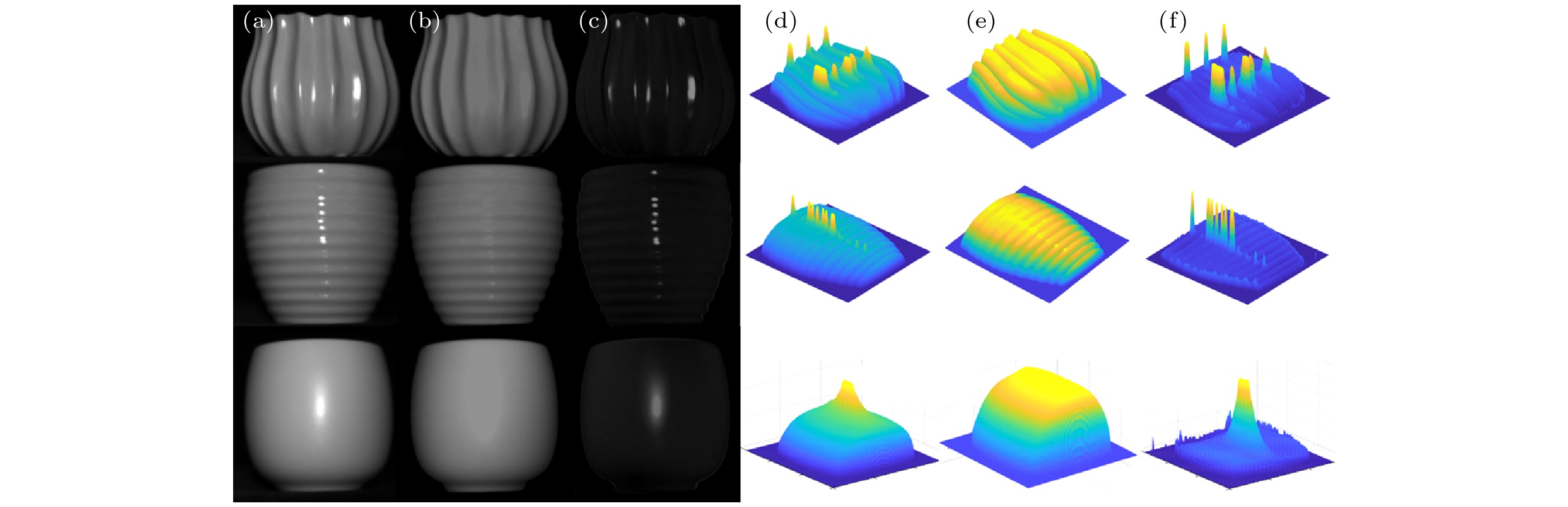
图 7 其他目标反射成分分离结果 (a) 总光强分布; (b), (c) 分离后的漫反射分量和镜面反射分量光强分布; (d), (e), (f) 分别为(a), (b), (c)的光强空间显示结果
Figure 7. Reflection separation of three different objects: (a) Total light intensity distribution; (b), (c) light intensity distributions of separated diffuse and specular reflection, respectively; (d), (e), (f) spatial display of (a), (b) and (c) respectively.
-
[1] Zhang W Z, Chen Z B, Xia B F, Lin B, Cao X Q 2014 Chin. Phys. B 23 044212
Google Scholar
[2] Salvi J, Pages J, Batlle J 2004 Pattern Recognit. 37 827
Google Scholar
[3] Varady T, Martin R R, Cox J 1997 Comput.-Aided Des. 29 255
Google Scholar
[4] 周光照, 王玉丹, 任玉琦, 陈灿, 叶琳琳, 肖体乔 2012 物理学报 61 018701
Google Scholar
Zhou G Z, Wang Y D, Ren Y Q, Chen C, Ye L L, Xiao T Q 2012 Acta Phys. Sin. 61 018701
Google Scholar
[5] Zhang R, Tsai P S, Cryer J E, Shah M 1999 IEEE Trans. Pattern Anal. Mach. Intell. 21 690
Google Scholar
[6] Jiang L, Zhang J Y, Deng B L, Li H, Liu L G 2018 IEEE Trans. Image Process. 27 4756
Google Scholar
[7] Shafer S A 1985 Color Res. Appl. 10 210
Google Scholar
[8] Klinker G J, Shafer S A, Kanade T 1988 Int. J. Comput. Vision 2 7
Google Scholar
[9] Klinker G J, Shafer S A, Kanade T 1990 Int. J. Comput. Vision 4 7
Google Scholar
[10] Novak C L, Shafer S A 1992 Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Champaign, USA, June 15–18, 1992 p599
[11] Tan P, Quan L, Lin S 2006 Proceedings 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition New York, USA, June 17–22, 2006 p1855
[12] Shen H L, Zheng Z H 2013 Appl. Opt. 52 4483
Google Scholar
[13] Ren W H, Tian J D, Tang Y D 2017 IEEE Trans. Image Process. 26 2327
Google Scholar
[14] Sato Y, Ikeuchi K 1994 J. Opt. Soc. Am. A: 11 2990
Google Scholar
[15] Wolff L B, Boult T E 1991 IEEE Trans. Pattern Anal. Mach. Intell. 13 635
Google Scholar
[16] Nayar S K, Fang X S, Boult T 1997 Int. J. Comput. Vision 21 163
Google Scholar
[17] Umeyama S J, Godin G 2004 IEEE Trans. Pattern Anal. Mach. Intell. 26 639
Google Scholar
[18] Atkinson G A, Hancock E R 2007 IEEE Trans. Pattern Anal. Mach. Intell. 29 2001
Google Scholar
[19] 王文波, 张晓东, 汪祥莉 2013 物理学报 62 050201
Google Scholar
Wang W B, Zhang X D, Wang X L 2013 Acta Phys. Sin. 62 050201
Google Scholar
[20] Comon P 1994 Signal Process. 36 287
Google Scholar
[21] TichavskÝ P, Kybernetika Z 2011 Kybernetika 47 426
[22] Hyvarinen A, Oja E 2000 Neural Networks 13 411
Google Scholar
[23] Adachi K, Trendafilov N T 2018 Psychometrika 83 407
Google Scholar
[24] Li Z, Liu D T, Ye T, Chen G H, Zhang L H, Yang Q S, Ji F 2007 Chin. Phys. Lett. 16 2913
Google Scholar
[25] Biglieri E, Yao K 1989 Signal Process. 18 277
Google Scholar
[26] 赵辽英, 吕步云, 厉小润, 陈淑涵 2015 物理学报 64 124204
Google Scholar
Zhao L Y, Lü B Y, Li X R, Chen S H 2015 Acta Phys.Sin. 64 124204
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7970
- PDF Downloads: 223
- Cited By: 0
