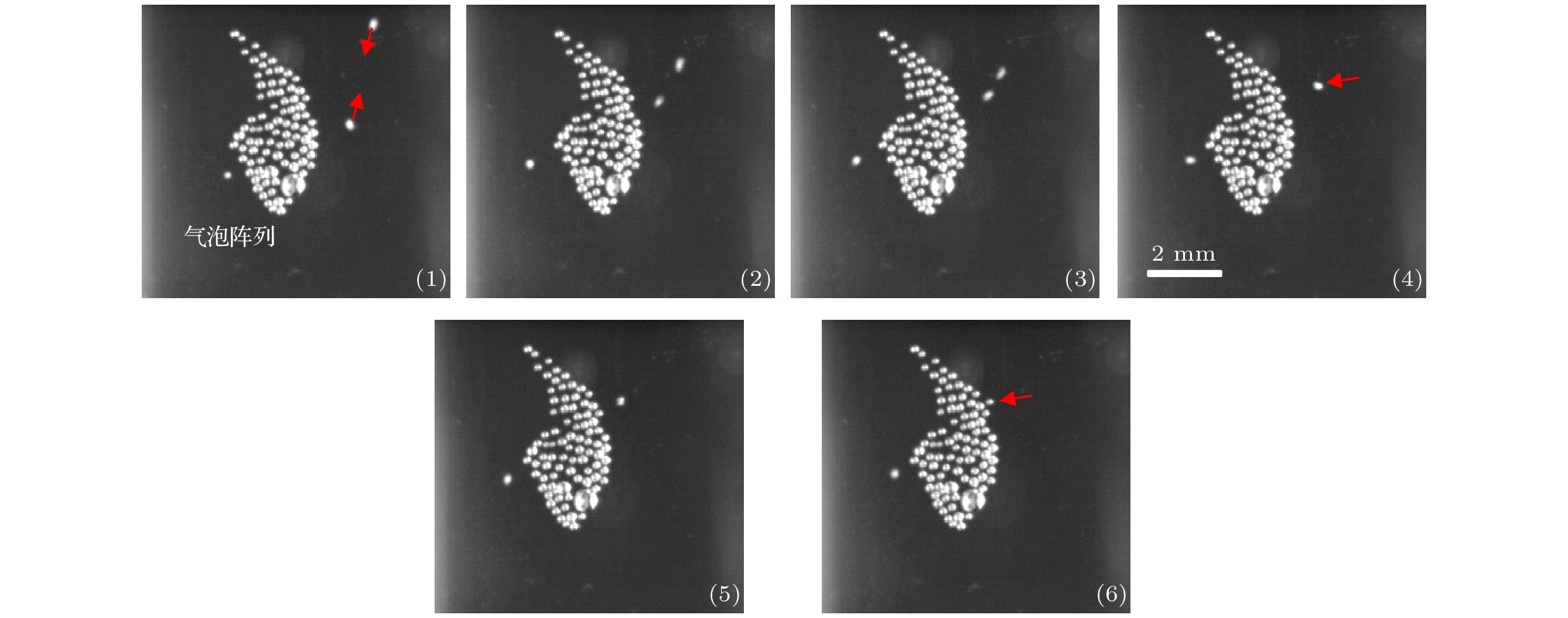
-
Bubbles in the fluid have a great influence on the macroscopic physical properties and flow state of the fluid. The study of bubble motion in fluid is of great significance to ultrasonic cleaning, sonochemistry, flood discharge and energy dissipation, aeration and cavitation reduction. Bubbles in the fluid may also exhibit a special translational motion in an ultrasonic field—orbital motion. The orbital motions of gas bubbles attached to a boundary in ultrasonic field are investigated experimentally by high-speed photography and image analysis. The present study focuses on the trajectories of wandering bubbles, the arrangement of gas bubble array, the source of gas bubbles and the surface fluctuation details of gas bubbles. It is found that the circular trajectory of the wandering gas bubble is unstable, irregular and unsmooth. The holding gas bubbles in the bubble array originate from wandering bubbles. The transformation of wandering bubbles into array bubbles is mainly realized by merging and increasing the volume, thereby reducing the Bjerknes force. The wandering bubbles are produced by the merging of a large number of cavitation bubbles in the ALF (acoustic lichtenberg figure) structure, which makes the radial vibration bubbles gradually transform into the surface fluctuating bubbles. Under the action of Bjerknes force, the array bubbles show regular surface fluctuations, while the smaller ones are completely unstable, showing extremely irregular morphology, and have an influence on the surface fluctuation of nearby array bubbles. The array bubbles show a very regular arrangement, and the adjacent array bubbles have opposite vibration phases and repel each other. The orbital motion of gas bubbles attached to a boundary is significantly different from that of the bubbles suspended in liquid. First of all, the attached bubbles move along the solid wall, while the suspended bubbles move completely away from the vessel wall in the liquid. Secondly, the attached bubbles move around a regular array of bubbles, while the suspended bubbles move orbitally alone. In addition, the attached bubble is nearly hemispherical, and its surface fluctuates violently, and its motion track is extremely unsmooth, which is different from the circular motion of spherical suspended bubble. Finally, there is a strong interaction between the attached wandering bubble and the array bubble, which has a great influence on the vibration and trajectory of the attached bubble. In contrast, the circular motion of the suspended bubble does not have such a complex effect.
-
Keywords:
- gas bubble /
- ultrasonic field /
- image processing /
- high-speed photogarphy
[1] Shew W L, Pinton J F 2006 Phys. Rev. Lett. 97 144508
Google Scholar
[2] Bai L X, Xu W L, Zhang Y C, Li Y F, Huang D F 2008 IEEE International Ultrasonics Symposium Proceedings Beijing, China, November 2–5, 2008 p942
[3] Young F R 1989 Cavitation (London: McGraw-Hill Book Company) p18
[4] Paul T, Richard M, Andrew O 2007 J. Fluid Mech. 576 191
Google Scholar
[5] 郭策, 祝锡晶, 王建青, 叶林征 2016 物理学报 65 044304
Google Scholar
Guo C, Zhu X J, Wang J Q, Ye L Z 2016 Acta Phys. Sin. 65 044304
Google Scholar
[6] Tomita Y, Shima A 1986 J. Fluid Mech. 169 535
Google Scholar
[7] Versluis M, Goertz D E, Palanchon P, Heitman I L, Van Der Meer S M, Dollet B, Jong N D, Lohse. D 2010 Phys. Rev. E 82 026321
Google Scholar
[8] Kim T, Kim H 2014 J. Fluid Mech. 750 355
Google Scholar
[9] Leighton T G, Walton A J, Pickworth M J W 1990 Eur. J. Phys. 11 47
Google Scholar
[10] Parlitzs B U, Mettin R, Luther S, Akhativ I, Voss M, Lauterborn W 1999 Philos. Trans. R. Soc. London, Ser. A 357 313
Google Scholar
[11] Metti R 2005 Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications (Kerala: Research Signpost Publisher) pp1−36
[12] Kodama T, Takayama K, Nagayasu N 1996 J. Appl. Phys 80 5587
Google Scholar
[13] Miller D L 1977 J. Acoust. Soc. Am. 62 12
Google Scholar
[14] Barbat T, Ashgritz N 2004 Appl. Math. Comput. 157 775
[15] Rensen J, Bosman D, Magnaudet J, Ohl C D, Prosperetti A, Togel R, Versluis M, Lohse D 2001 Phys. Rev. Lett. 86 4819
Google Scholar
[16] Shirota M, Yamashita K, Inamura T 2012 American Institute of Physics Conference Proceedings New Mexico, April 30–May 3, 2012 p155
[17] Desjouy C, Labelle P, Gilles B, Bera J C, Inserra C 2013 Phys. Rev. E 88 033006
Google Scholar
[18] Desjouy C, Labelle P, Gilles B, Bera JC, Inserra C 2013 J. Acoust. Soc. Am. 133 3277
[19] Bai L X, Xu W L, Deng J J, Li C, Xu D L, Gao Y D 2014 Ultrason. Sonochem. 21 1696
Google Scholar
[20] Bai L X, Xu W L, Zhang F X, Li N W, Zhang Y C, Huang D F 2009 Sci China Ser. E 52 1974
Google Scholar
-
图 1 实验装置图
Figure 1. Experimental setup.
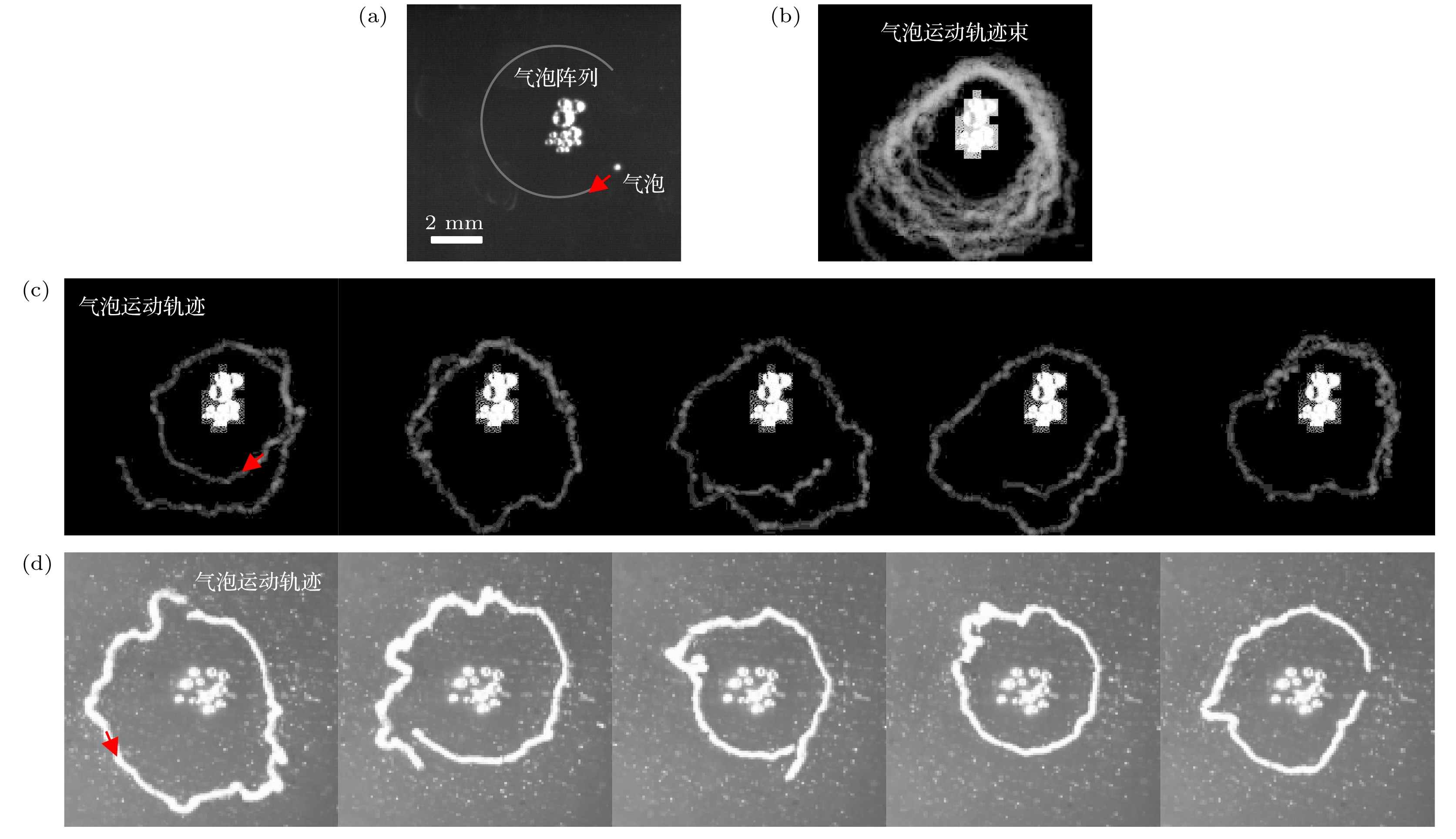
图 2 超声场中附壁气泡的绕圈运动 (a) 气泡绕圈运动的快照; (b) 图(a)中气泡运动轨迹束; (c) 图(a)中气泡单圈运动轨迹(影像叠加); (d) 气泡单圈运动轨迹(长时曝光)
Figure 2. Orbital motion of a gas bubble attached to a boundary in ultrasonic field: (a) Snapshot of the orbital motion of a gas bubble; (b) trajectories of the gas bubble in Fig.2(a); (c) single loop trajectory of the gas bubble in Fig. 2(a) (image overlay); (d) single loop trajectory of the gas bubble in Fig. 2(a) (long exposure).
图 3 超声场中附壁气泡的布阵过程
Figure 3. The arrangement of gas bubbles attached to the boundary in ultrasonic field.
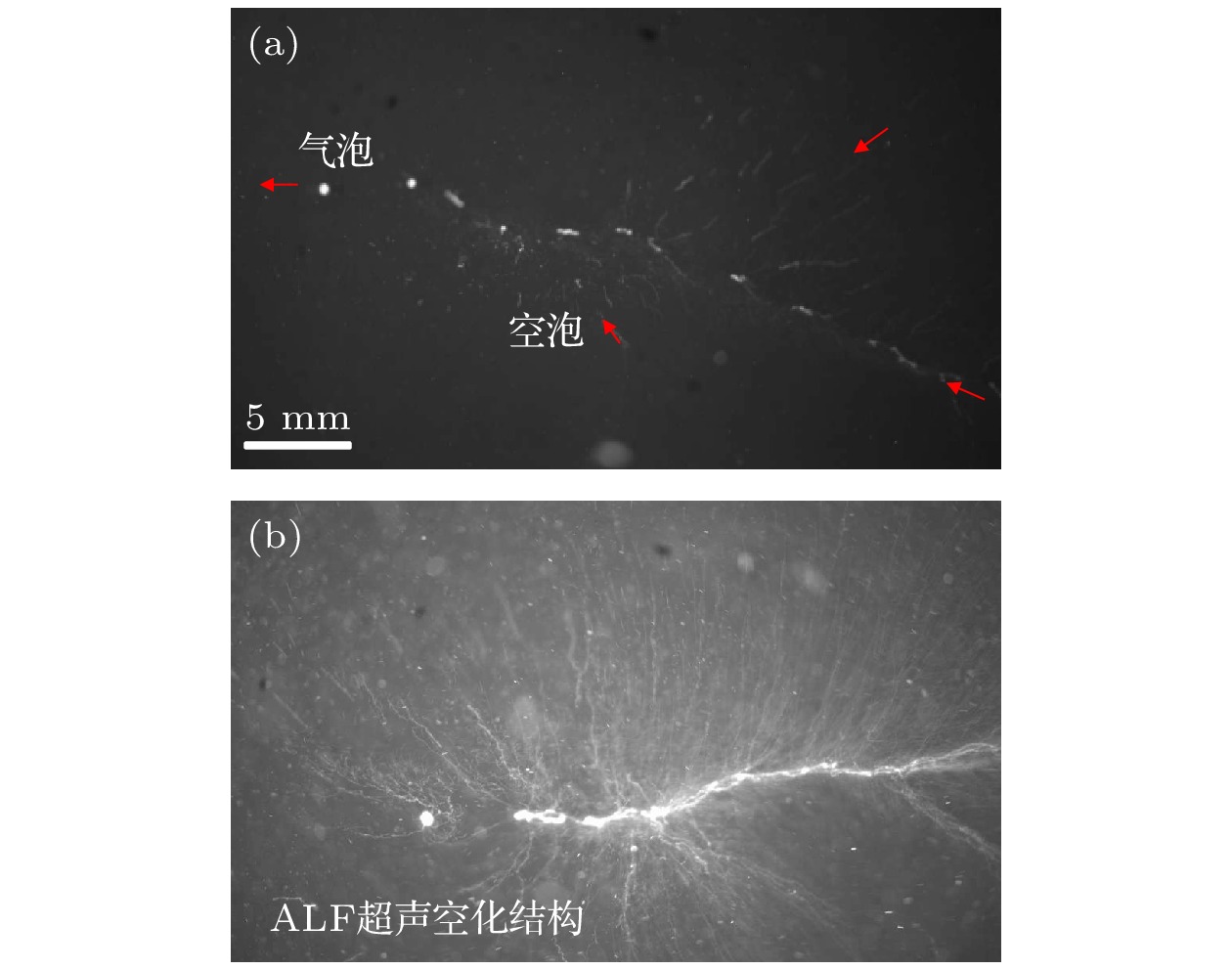
图 4 超声场中附壁气泡的来源 (a) ALF超声空化云中空泡的运动和气泡的形成(曝光时间1/250 s); (b) ALF超声空化云中空泡和气泡的运动轨迹(曝光时间1/50 s)
Figure 4. The source of gas bubbles attached to the wall in ultrasonic field: (a) The motion of cavitation bubbles and the formation of gas bubbles in ALF structure (the exposure time is 1/250 s); (b) trajectories of cavitation bubbles and gas bubbles in ALF structure (the exposure time is 1/50 s).
图 5 绕圈气泡与附壁气泡的表面形态
Figure 5. Surface morphology of wandering gas bubble and holding bubble.
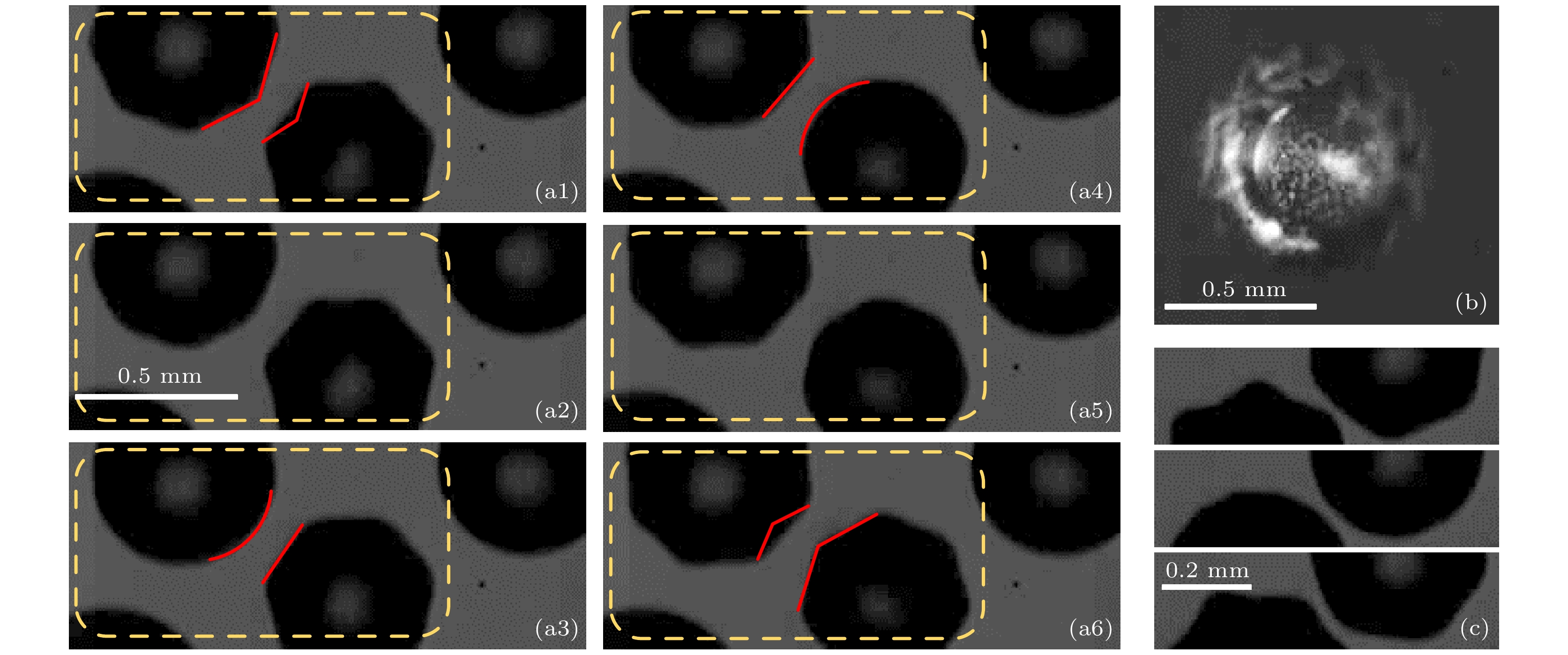
图 6 附壁气泡的表面波动 (a) 附壁气泡阵列中相邻气泡半个周期内表面波动的耦合(拍摄速度为100000 frame/s); (b) 反射光照射下附壁气泡的表面波动; (c) 相距极近的两个气泡的振动耦合
Figure 6. Surface wave of gas bubble attached to the boundary: (a) Surface fluctuation of adjacent gas bubbles in a bubble array in half a period (Frame rate: 100000 frame/s); (b) surface fluctuation of a gas bubble attached to boundary under reflected light; (c) wave coupling of two gas bubbles quite close to each other.
-
[1] Shew W L, Pinton J F 2006 Phys. Rev. Lett. 97 144508
Google Scholar
[2] Bai L X, Xu W L, Zhang Y C, Li Y F, Huang D F 2008 IEEE International Ultrasonics Symposium Proceedings Beijing, China, November 2–5, 2008 p942
[3] Young F R 1989 Cavitation (London: McGraw-Hill Book Company) p18
[4] Paul T, Richard M, Andrew O 2007 J. Fluid Mech. 576 191
Google Scholar
[5] 郭策, 祝锡晶, 王建青, 叶林征 2016 物理学报 65 044304
Google Scholar
Guo C, Zhu X J, Wang J Q, Ye L Z 2016 Acta Phys. Sin. 65 044304
Google Scholar
[6] Tomita Y, Shima A 1986 J. Fluid Mech. 169 535
Google Scholar
[7] Versluis M, Goertz D E, Palanchon P, Heitman I L, Van Der Meer S M, Dollet B, Jong N D, Lohse. D 2010 Phys. Rev. E 82 026321
Google Scholar
[8] Kim T, Kim H 2014 J. Fluid Mech. 750 355
Google Scholar
[9] Leighton T G, Walton A J, Pickworth M J W 1990 Eur. J. Phys. 11 47
Google Scholar
[10] Parlitzs B U, Mettin R, Luther S, Akhativ I, Voss M, Lauterborn W 1999 Philos. Trans. R. Soc. London, Ser. A 357 313
Google Scholar
[11] Metti R 2005 Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications (Kerala: Research Signpost Publisher) pp1−36
[12] Kodama T, Takayama K, Nagayasu N 1996 J. Appl. Phys 80 5587
Google Scholar
[13] Miller D L 1977 J. Acoust. Soc. Am. 62 12
Google Scholar
[14] Barbat T, Ashgritz N 2004 Appl. Math. Comput. 157 775
[15] Rensen J, Bosman D, Magnaudet J, Ohl C D, Prosperetti A, Togel R, Versluis M, Lohse D 2001 Phys. Rev. Lett. 86 4819
Google Scholar
[16] Shirota M, Yamashita K, Inamura T 2012 American Institute of Physics Conference Proceedings New Mexico, April 30–May 3, 2012 p155
[17] Desjouy C, Labelle P, Gilles B, Bera J C, Inserra C 2013 Phys. Rev. E 88 033006
Google Scholar
[18] Desjouy C, Labelle P, Gilles B, Bera JC, Inserra C 2013 J. Acoust. Soc. Am. 133 3277
[19] Bai L X, Xu W L, Deng J J, Li C, Xu D L, Gao Y D 2014 Ultrason. Sonochem. 21 1696
Google Scholar
[20] Bai L X, Xu W L, Zhang F X, Li N W, Zhang Y C, Huang D F 2009 Sci China Ser. E 52 1974
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5063
- PDF Downloads: 104
- Cited By: 0
