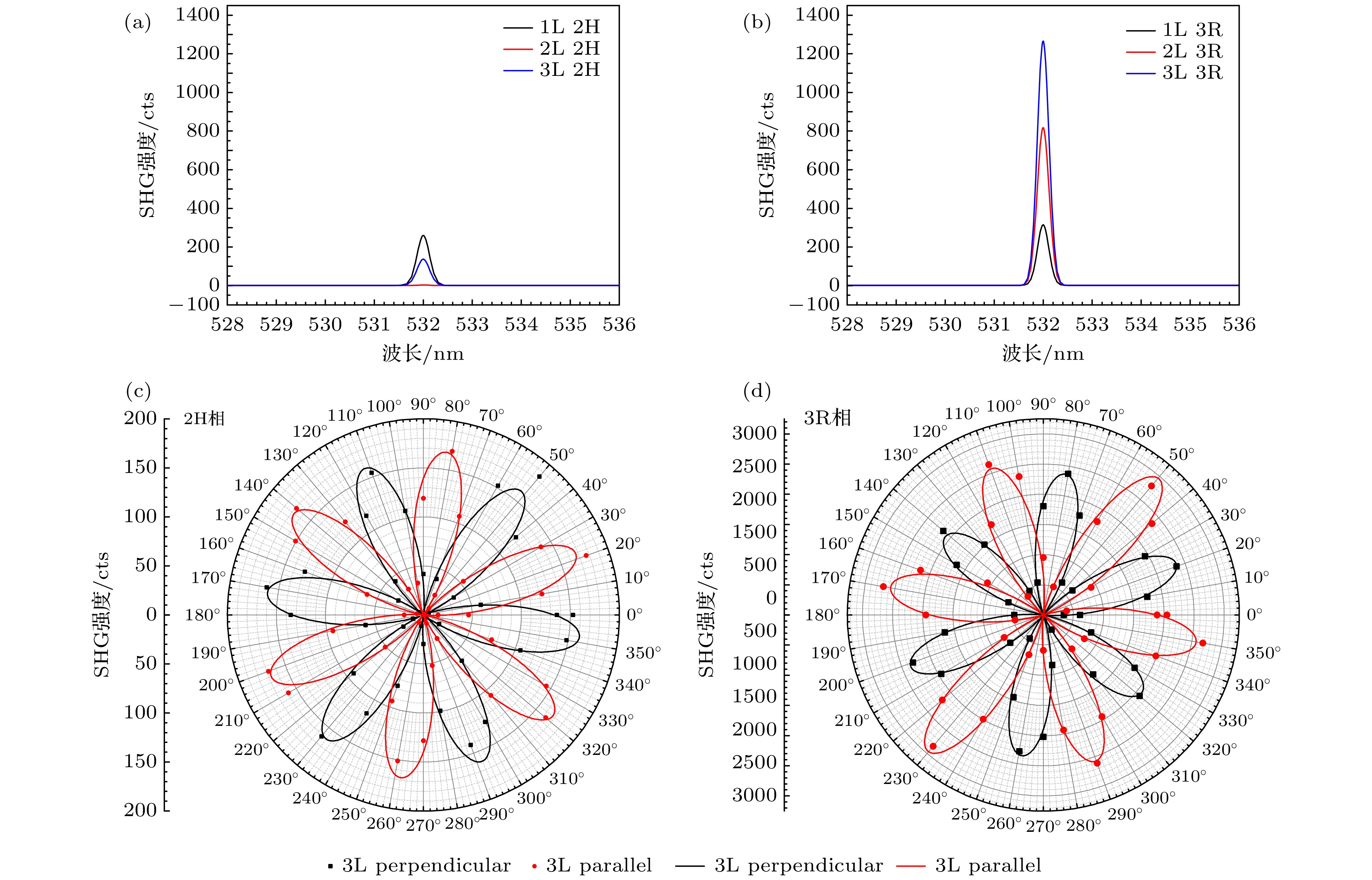
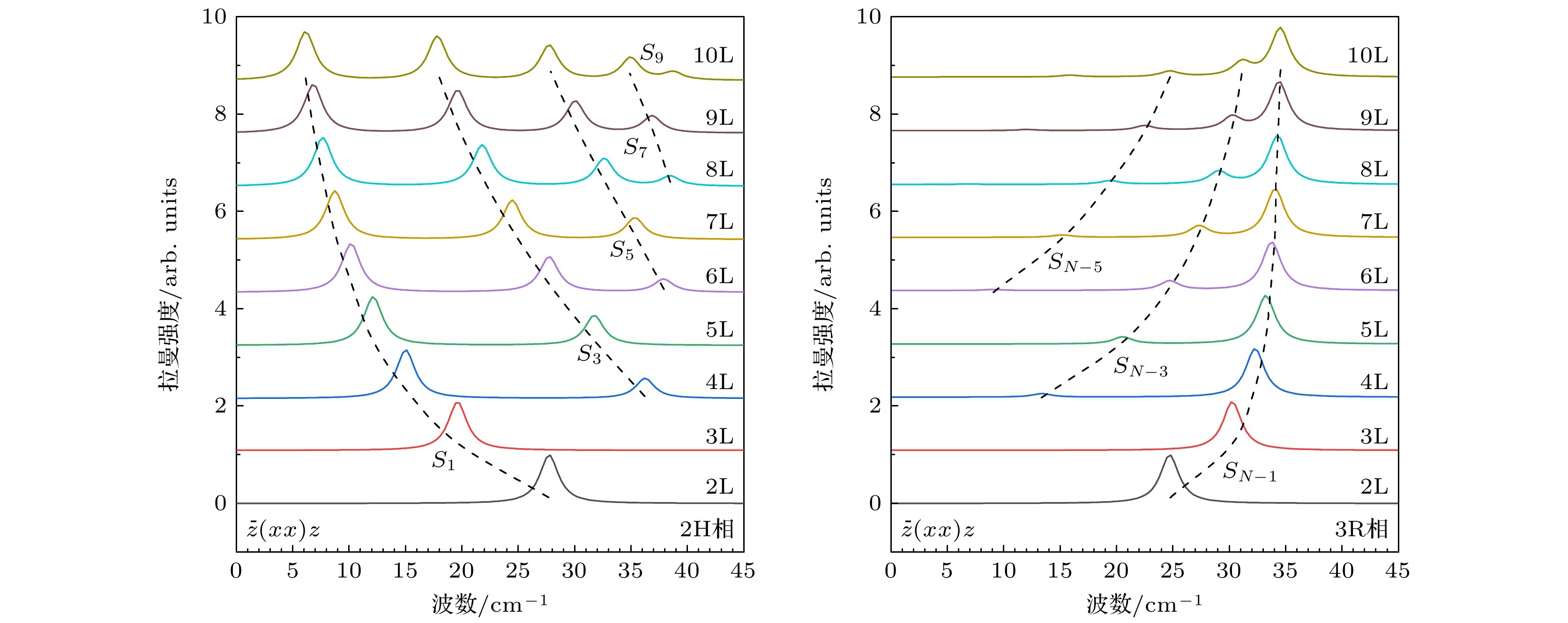
-
Layered transition metal dichalcogenides (TMDs) have attracted extensive interest due to their remarkable electronic, optical, and mechanical properties. Among them, molybdenum disulfide (MoS2) exhibits two main stacking polytypes: the centrosymmetric 2H phase and the non-centrosymmetric 3R phase. The latter has recently drawn attention for its spontaneous polarization, piezoelectricity, band modulation, and possible topological features, but its lattice dynamics and phonon-related properties remain far less understood. To address this gap, we present a comprehensive study of the layer-dependent Raman phonon characteristics of 3R-phase MoS2 and systematically compare them with those of the 2H phase.Experimentally, we employed confocal Raman spectroscopy and polarization-resolved second-harmonic generation (SHG) to probe vibrational modes and stacking-dependent nonlinear responses of samples ranging from monolayer to bulk. SHG measurements provided an unambiguous means of distinguishing the stacking orders: while the SHG signal vanishes in even-layer 2H samples due to inversion symmetry, it persists strongly in 3R samples of any thickness. Raman spectra in the low-frequency region revealed distinct shear and breathing modes whose evolution with layer number was analyzed using both the linear chain model (LCM) and the more refined force constant model (FCM). While the LCM qualitatively captures the layer-dependent shifts of interlayer vibrations, the FCM provides quantitative agreement with experiments by explicitly incorporating nearest- and next-nearest-neighbor interactions as well as surface corrections.To further interpret the relative intensities of interlayer Raman modes, we introduced the bond polarization model (BPM), which links mode-dependent scattering strength to the symmetry and orientation of chemical bonds. Our BPM analysis revealed pronounced asymmetry in charge redistribution for 3R stacking, leading to weaker interlayer binding energy compared to 2H (0.111 eV vs. 0.113 eV), and consequently a lower sliding barrier, consistent with the observed propensity of 3R crystals for interlayer slip. In the high-frequency region, both stacking types show characteristic in-plane and out-of-plane modes; however, the peak separation in 3R-phase MoS2 demonstrates stronger sensitivity to the layer number, making it a more reliable spectroscopic fingerprint for thickness identification. Importantly, we found that surface effects play a critical role in reproducing experimental high-frequency shifts in 3R samples, reflecting their weaker interlayer coupling and enhanced surface contributions.In summary, this work establishes a complete picture of the phonon behavior in 3R-phase MoS2, bridging experiment and theory. Our results demonstrate that Raman spectroscopy combined with SHG provides a powerful toolkit for identifying stacking order and thickness in layered MoS2. By benchmarking LCM, FCM, and BPM models, we clarify the roles of interlayer coupling, stacking symmetry, and surface effects in shaping vibrational properties. These insights not only advance the fundamental understanding of lattice dynamics in non-centrosymmetric TMD polytypes, but also lay the groundwork for exploiting 3R-phase MoS2 in next-generation optoelectronic, piezoelectric, and quantum devices.
-
Keywords:
- 3R-phase MoS2 /
- linear chain model (LCM) /
- force constant model (FCM) /
- bond polarization model (BPM)
-
图 1 (a) 3R相MoS2俯视图与侧视图; (b) 单层MoS2的6种声子模式, 峰位采用cm–1为单位; 单层、三层和块体的(c) 2H相和(d) 3R相MoS2拉曼谱线
Figure 1. (a) Top view and side view of 3R-phase MoS2; (b) six phonon modes of monolayer MoS2, peak positions in cm–1; Raman spectra of (c) 2H-phase and (d) 3R-phase MoS2 for monolayer, trilayer, and bulk.
图 2 1—3层(a) 2H相和(b) 3R相MoS2的SHG响应; 3层(c) 2H相和(d) 3R相MoS2的偏振SHG极图
Figure 2. SHG responses of 1–3 layer (a) 2H-phase and (b) 3R-phase MoS2; polarization-dependent SHG polar plots of trilayer (c) 2H-phase and (d) 3R-phase MoS2.
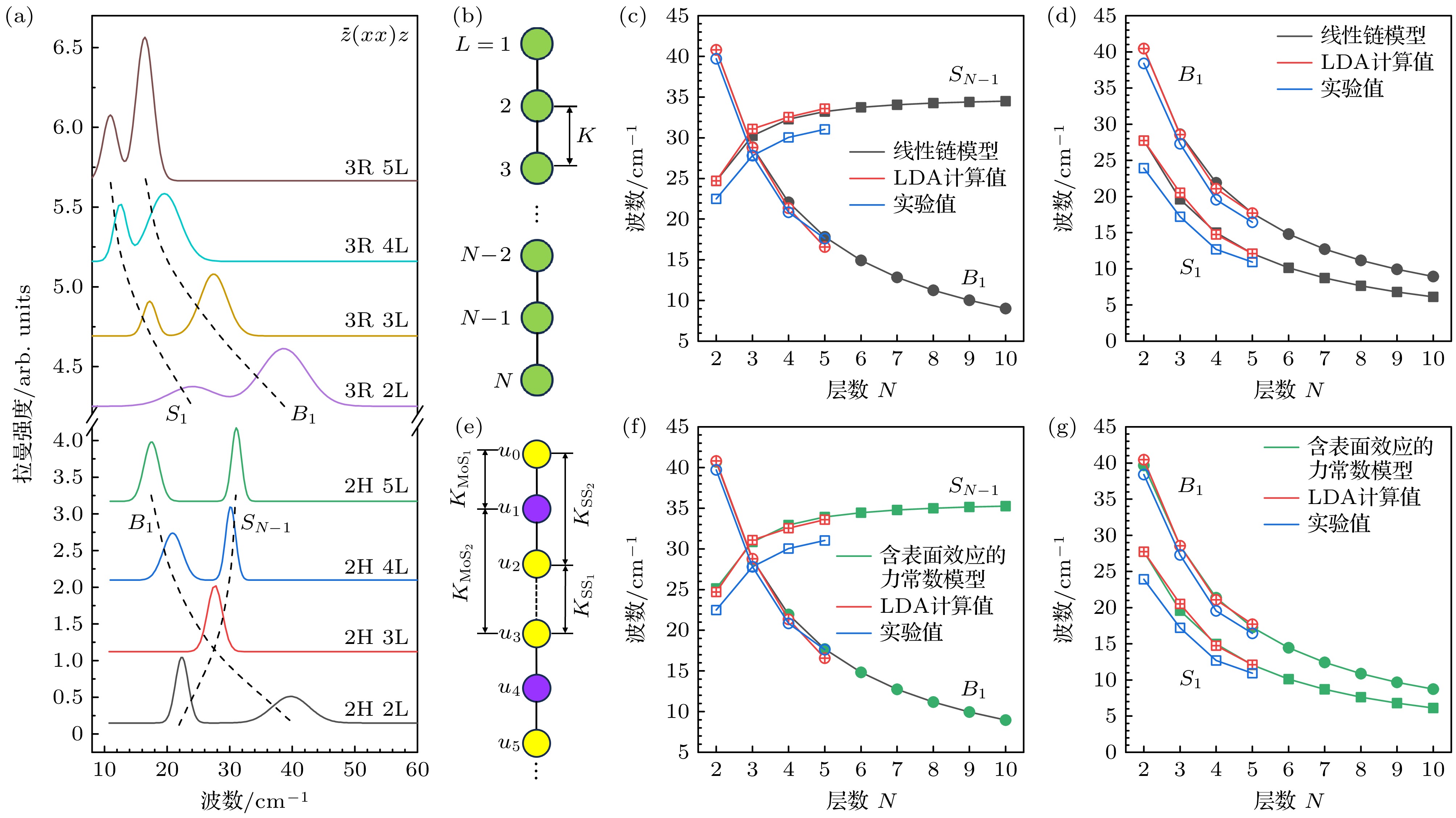
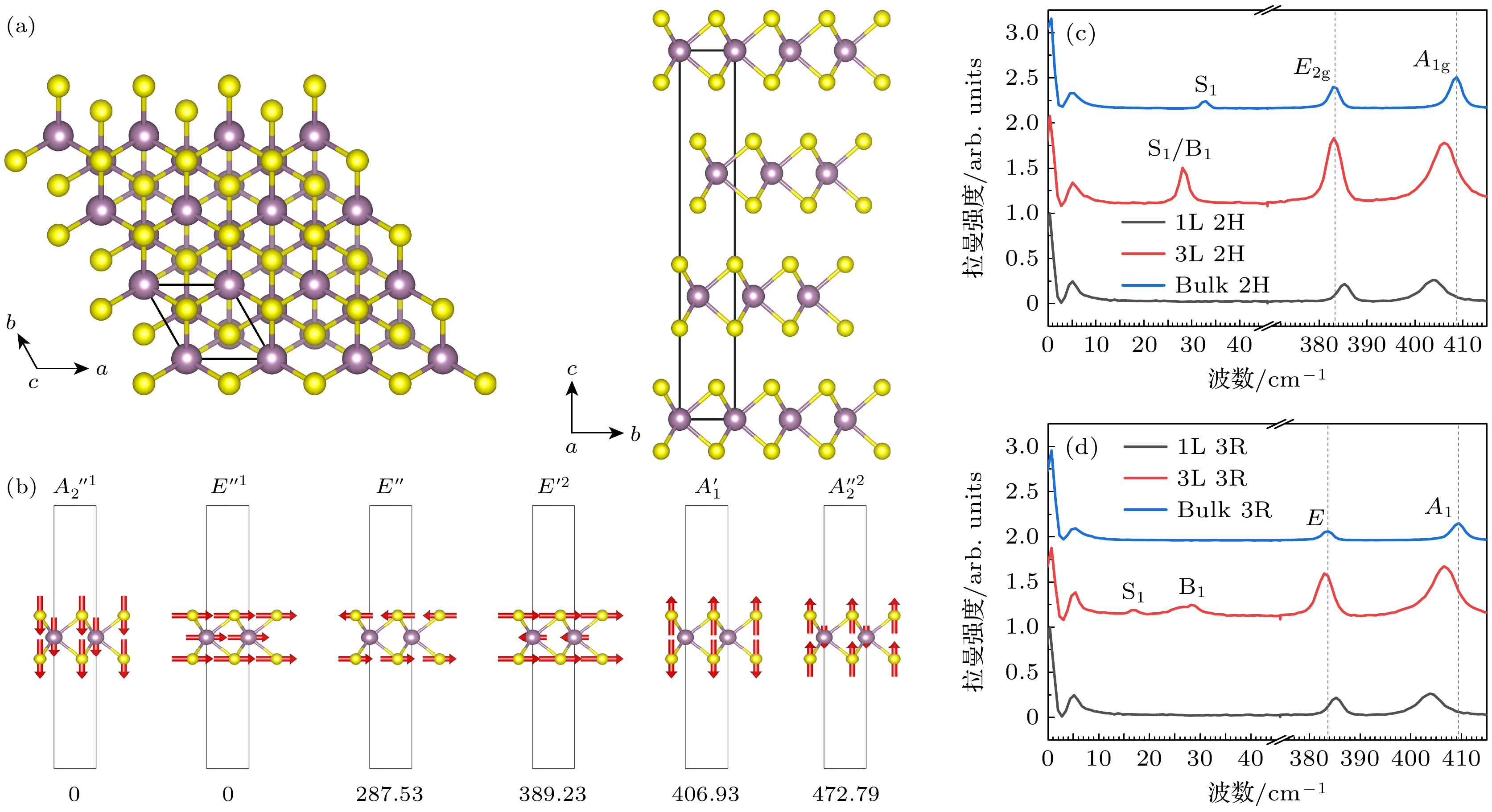
图 3 (a) 平行偏振下2—5层2H和3R相MoS2低波数拉曼谱线; (b) 线性链模型; 线性链模型对(c) 2H相和(d) 3R相的低波数峰拟合结果; (e) 力常数模型; 力常数模型对(f) 2H和(g) 3R相的低波数峰拟合结果
Figure 3. (a) Low-frequency Raman spectra of 2–5 layer 2H- and 3R-phase MoS2 under parallel polarization. (b) Linear chain model; fitting results of low-frequency peaks for (c) 2H-phase and (d) 3R-phase MoS2 using the linear chain model. (e) Force constant model; fitting results of low-frequency peaks for (f) 2H-phase and (g) 3R-phase MoS2 using the force constant model.
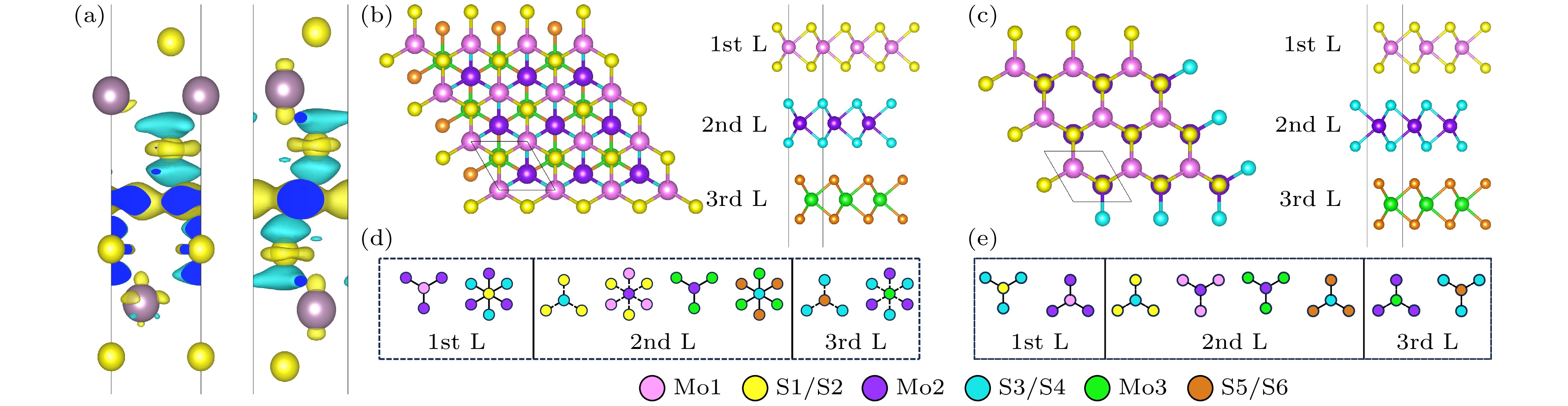
图 4 (a) 双层3R相(左)和2H相(右)MoS2的差分电荷图; 三层(b) 3R相和(c) 2H相MoS2的俯视图和侧视图; 三层(d) 3R相和(e) 2H相MoS2的键极化分析图, 其中虚线表示向上连接的键, 实线表示向下连接的键, $ {\rm{S_i}} $、$ {\rm{Mo_i}} $和$ {\rm{S_{i+1}}} $分别依次表示第i层从上至下的S、Mo和S原子
Figure 4. (a) Differential charge density maps of bilayer 3R-phase (left) and 2H-phase (right) MoS2. Top and side views of trilayer (b) 3R-phase and (c) 2H-phase MoS2. Bond polarization analysis of trilayer (d) 3R-phase and (e) 2H-phase MoS2, where dashed lines denote upward bonds and solid lines denote downward bonds. $ {\rm{S_i}} $, $ {\rm{Mo_i}} $, and $ {\rm{S_{i+1}}} $ represent the S, Mo, and S atoms in the i-th layer from top to bottom, respectively.
图 5 键极化模型得到的2H(左)和3R(右)堆叠方式层间拉曼强度图
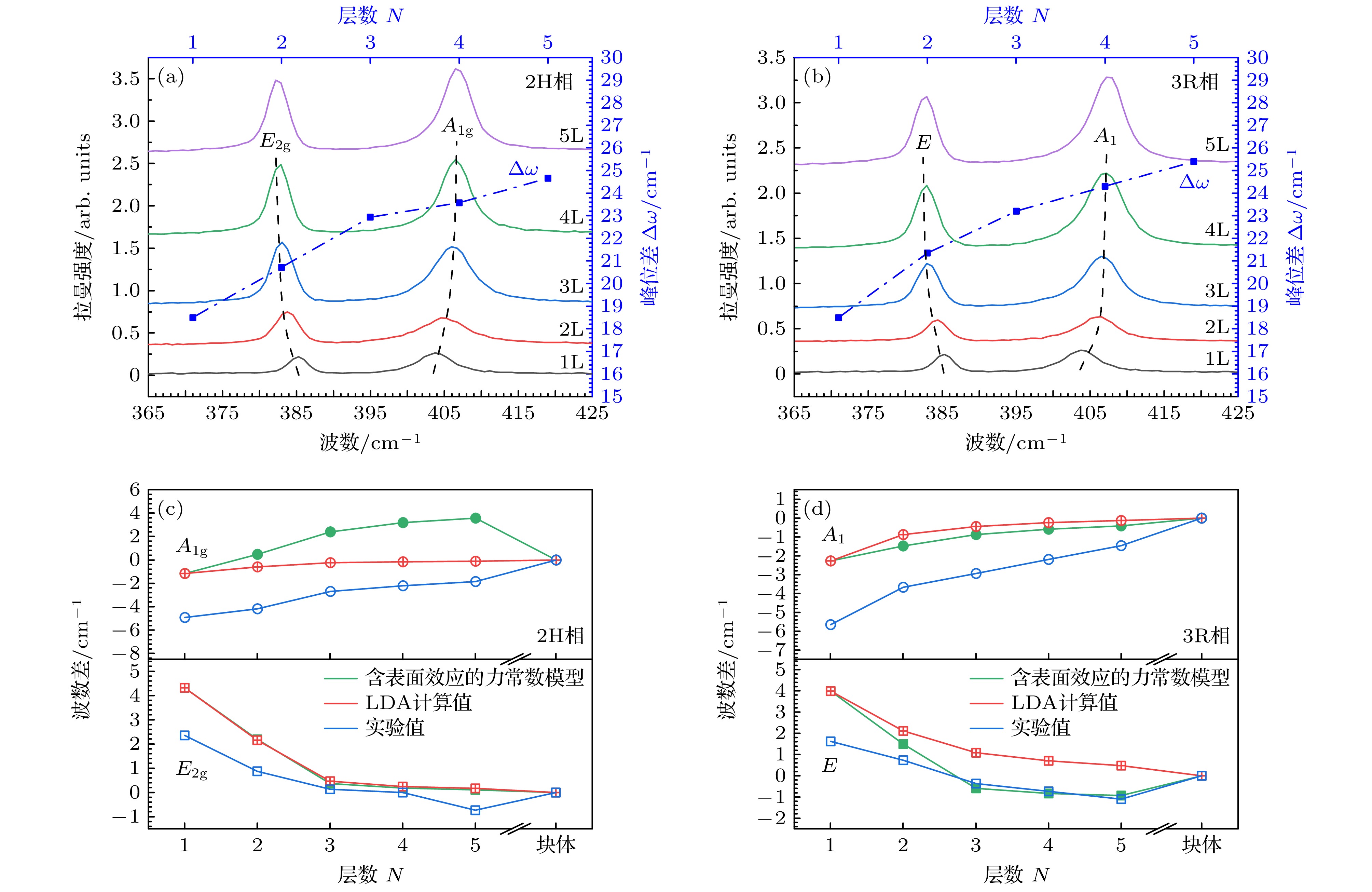
Figure 5. Interlayer Raman intensity maps obtained from the bond polarization model for 2H (left) and 3R (right) stacking configurations.
图 6 (a) 2H和(b) 3R相MoS2高频峰位及其峰位差; (c)和(d)为引入表面效应的力常数模型对高频峰位的拟合, 其中峰位差均是通过块体的频率计算得到的
Figure 6. High-frequency peak positions of (a) 2H-phase and (b) 3R-phase MoS2, together with their peak differences. (c) and (d) show the fitting of high-frequency peak positions using the force constant model with surface effects included, where the peak differences are obtained from the calculated bulk frequencies.
图 A1 3R相MoS2的18种声子模式, 峰位采用cm–1为单位
Figure A1. The 18 phonon modes of 3R-phase MoS2, with peak positions given in cm–1
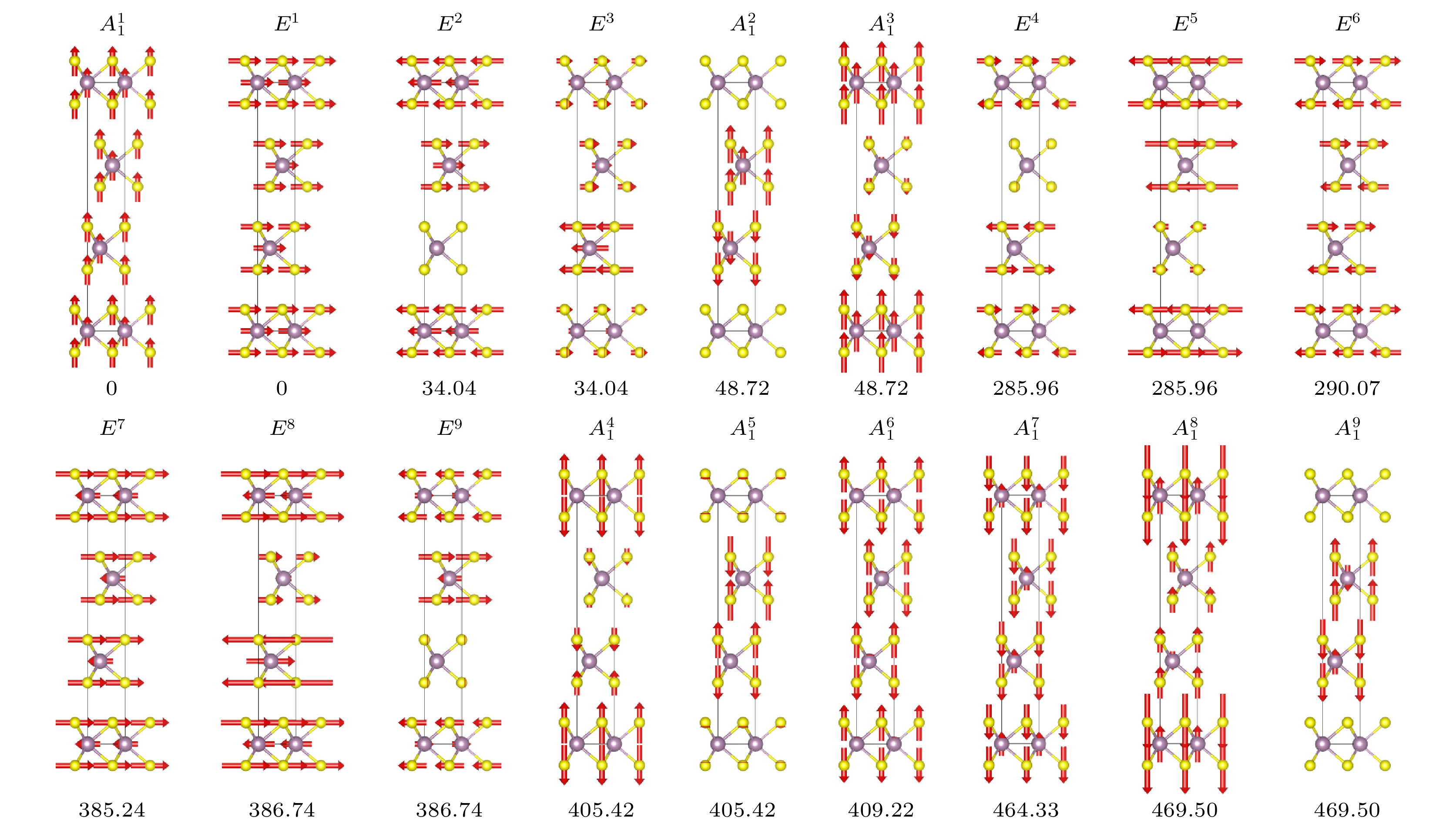
表 1 MoS2体系振动模式的不可约表示、实验测量频率和理论计算频率汇总
Table 1. Summary of the force constant values for 3R phase MoS2.
Phase Irr. rep. Exp. LDA LDA Exp. Irr. rep. Phase 2H $ E_{1 u} $(I) - 0 0 - $ A_{1} $(I+R) 3R $ A_{2 u} $(I) - 0 0 - E(I+R) $ E_{2 g} $(R) 33.29487 35.686900 34.037372 - E(I+R) $ B_{1 g} $ - 57.941155 34.037596 - E(I+R) $ E_{2 u} $ - 285.155367 48.724024 - $ A_{1} $(I+R) $ E_{1 g} $(R) - 287.775743 48.724325 - $ A_{1} $(I+R) $ E_{2 g} $(R) 384.917714 384.976788 285.957612 - E(I+R) $ E_{1 u} $(I) - 385.716750 285.958139 - E(I+R) $ B_{2 u} $ - 404.033206 290.072680 - E(I+R) $ A_{1 g} $(R) 409.04906 408.106024 385.242202 383.66260 E(I+R) $ A_{2 u} $(I) - 465.182502 386.741898 - E(I+R) $ B_{1 g} $ - 468.960303 386.742311 - E(I+R) 1H $ E' $(I+R) - 0 405.420245 - $ A_{1} $(I+R) $ A_2'' $(I) - 0 405.420515 - $ A_{1} $(I+R) $ E'' $(R) - 287.529971 409.217160 409.42571 $ A_{1} $(I+R) $ E' $(I+R) 385.28101 389.234675 464.326446 - $ A_{1} $(I+R) $ A_1' $(R) 403.77329 406.934400 469.500655 - $ A_{1} $(I+R) $ A_2'' $(I) - 472.790370 469.501212 - $ A_{1} $(I+R) 注: I表示具有红外活性, R表示具有拉曼活性, 频率均以cm–1为单位 
DownLoad: CSV
表 2 MoS2力常数模型各阶力常数系数汇总
Table 2. Summary of the force constant values for 3R phase MoS2.
力常数
类型面内模式(N/m) 面外模式(N/m) 2H块体 3R块体 单层 2H块体 3R块体 单层 $ K_{{\rm{MoS1}}} $ 4.236801 4.21876 4.34525 6.18676 6.15929 6.41101 $ K_{{\rm{MoS2}}} $ 0.03023 0.03780 - 0.01955 0.02427 - $ K_{{\rm{SS1}}} $ 0.01571 0.01715 - 0.16477 0.14432 - $ K_{{\rm{SS2}}} $ –0.188220 –0.18916 –0.19479 0.80216 0.77007 0.75612
DownLoad: CSV
-
[1] Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A 2011 Nat. Nanotechnol. 6 147
Google Scholar
[2] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805
Google Scholar
[3] 李璐, 张养坤, 时东霞, 张广宇 2022 物理学报 71 108102
Google Scholar
Li L, Zhang Y K, Shi D X, Zhang G Y 2022 Acta Phys. Sin. 71 108102
Google Scholar
[4] Chhowalla M, Shin H S, Eda G, Li L J, Loh K P, Zhang H 2013 Nat. Chem. 5 263
Google Scholar
[5] 蒋彬, 丁宇龙, 赵福利, 罗鑫 2022 物理与工程 32 24
Google Scholar
Jiang B, Ding Y L, Zhao F L, Luo X 2022 Physics and Engineering 32 24
Google Scholar
[6] Meng P, Wu Y Z, Bian R J, Pan E, Dong B, Zhao X X, Chen J G, Wu L S, Sun Y Q, Fu Q D, Liu Q 2022 Nat. Commun. 13 7696
Google Scholar
[7] Hallil H, Cai W F, Zhang K, Yu P, Liu S, Xu R, Zhu C, Xiong Q H, Liu Z, Zhang Q 2022 Adv. Electron. Mater. 8 2101131
Google Scholar
[8] Akashi R, Ochi M, Bordács S, Suzuki R, Tokura Y, Iwasa Y, Arita R 2015 Phys. Rev. Appl. 4 014002
Google Scholar
[9] Wu J D, Yang D Y, Liang J, Werner M, Ostroumov E, Xiao Y H, Watanabe K, Taniguchi T, Dadap J I, Jones D, Ye Z L 2022 Sci. Adv. 8 eade3759
Google Scholar
[10] Wieting T 1973 Solid State Commun. 12 931
Google Scholar
[11] Luo N, Ruggerone P, Toennies J P 1996 Phys. Rev. B 54 5051
Google Scholar
[12] Tan P H, Han W P, Zhao W J, Wu Z H, Chang K, Wang H, Wang Y F, Bonini N, Marzari N, Pugno N 2012 Nat. Mater. 11 294
Google Scholar
[13] Zhao Y Y, Luo X, Li H, Zhang J, Araujo P T, Gan C K, Wu J, Zhang H, Quek S Y, Dresselhaus M S, Hua X Q 2013 Nano Lett. 13 1007
Google Scholar
[14] Luo X, Zhao Y Y, Zhang J, Xiong Q H, Quek S Y 2013 Phys. Rev. B 88 075320
Google Scholar
[15] Luo X, Lu X, Cong C X, Yu T, Xiong Q H, Ying Quek S 2015 Sci. Rep. 5 14565
Google Scholar
[16] Van Baren J, Ye G H, Yan J A, Ye Z P, Rezaie P, Yu P, Liu Z, He R, Lui C H 2019 2 D Mater. 6 025022
[17] Shi J, Yu P, Liu F C, He P, Wang R, Qin L, Zhou J B, Li X, Zhou J D, Sui X Y 2017 Adv. Mater. 29 1701486
Google Scholar
[18] Zeng Z X S, Sun X X, Zhang D L, Zheng W H, Fan X P, He M, Xu T, Sun L, Wang X, Pan A L 2019 Adv. Funct. Mater. 29 1806874
Google Scholar
[19] Balla N K, O’ brien M, McEvoy N, Duesberg G S, Rigneault H, Brasselet S, McCloskey D 2018 ACS Photonics 5 1235
Google Scholar
[20] Li Y L, Rao Y, Mak K F, You Y M, Wang S Y, Dean C R, Heinz T F 2013 Nano Lett. 13 3329
Google Scholar
[21] Kumar N, Najmaei S, Cui Q N, Ceballos F, Ajayan P M, Lou J, Zhao H 2013 Phys. Rev. B 87 161403
Google Scholar
[22] Malard L M, Alencar T V, Barboza A P M, Mak K F, De Paula A M 2013 Phys. Rev. B 87 201401
Google Scholar
[23] Khan A R, Zhang L, Ishfaq K, Ikram A, Yildrim T, Liu B, Rahman S, Lu Y 2022 Adv. Funct. Mater. 32 2105259
Google Scholar
[24] Lazzeri M, Mauri F 2003 Phys. Rev. Lett. 90 036401
Google Scholar
DownLoad:
Metrics
- Abstract views: 366
- PDF Downloads: 12
- Cited By: 0
