-
利用变分近似及基于Gross-Pitaevskii方程的直接数值模拟方法, 研究了自旋-轨道耦合玻色-爱因斯坦凝聚体中线性塞曼劈裂对亮孤子动力学的影响, 发现线性塞曼劈裂将导致体系具有两个携带有限动量的静态孤子, 以及它们在微扰下存在一个零能的Goldstone激发模和一个频率与线性塞曼劈裂有关的谐振激发模. 同时给出了描述孤子运动的质心坐标表达式, 发现线性塞曼劈裂明显影响孤子的运动速度和振荡周期.
-
关键词:
- 孤子 /
- 玻色-爱因斯坦凝聚 /
- Gross-Pitaevskii方程 /
- 自旋-轨道耦合
Solitons as self-supported solitary waves are one of the most fundamental objects in nonlinear science. With the realization of Bose-Einstein condensate, matter-wave solitons have aroused enormous interest due to their potential applications in atomic transport and atomic interferometer. In recent years, the artificial spin-orbit coupling has been realized in ultracold atoms, thus providing a new platform to study the nonlinear matter wave solitons under a gauge field, and a variety of novel soliton phenomena have been successively predicted. In this paper, we analyze the effects of linear Zeeman splitting on the dynamics of bright-bright solitons in spin-orbit coupled two-component Bose-Einstein condensate, via the variational approximation and the numerical simulation of Gross-Pitaevskii (GP) equations. For the SU(2) spin-rotational invariant attractive atomic interaction in a uniform case without external trap, we take a hyperbolic secant function as the variational Ansatz for bright soliton in variational approximation, and derive the Euler-Lagrange equations describing the evolution of the Ansatz parameters. By solving the time-independent Euler-Lagrange equations, we find two stationary solitons each with a finite momentum for a weak spin-orbit coupling due to the linear Zeeman splitting. Linearizing the Euler-Lagrange equations around these stationary solitons, we further obtain a zero-energy Goldstone mode and an oscillation mode with frequency related to linear Zeeman splitting: the former indicates that the continuous translational symmetry of the stationary solitons will be broken under a perturbation, and the later shows that the stationary solitons will oscillate under a perturbation. Furthermore, by solving the time-dependent Euler-Lagrange equations, we also obtain the exact full dynamical solutions of Ansatz parameters, and observe that the linear Zeeman splitting affects the period and velocity of soliton's oscillation and linear motion, which may provide a new method to control the dynamics of solitons. All the variational calculations are also confirmed directly by the numerical simulation of GP equations.-
Keywords:
- soliton /
- Bose-Einstein condensate /
- Gross-Pitaevskii equation /
- spin-orbit coupling
[1] Malomed B A 2006 Soliton Management in Periodic Systems (Vol. 1) (Berlin: Springer) p1
[2] Kevrekidis P G, Frantzeskakis D J, Carretero-Gonzalez R 2008 Emergent Nonlinear Phenomena in Bose-Einstein Condensates (Vol. 1)(Berlin: Springer) pp43−96
[3] Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K, Sanpera A, Shlyapnikov G V, Lewenstein M 1999 Phys. Rev. Lett. 83 5198
Google Scholar
[4] Khaykovich L, Schreck F, Ferrari G, Bourdel T, Cubizolles J, Carr L D, Castin Y, Salomon C 2002 Science 296 1290
Google Scholar
[5] Strecker K E, Partridge G B, Truscott A G, Hulet R G 2002 Nature 417 150
Google Scholar
[6] Cornish S L, Thompson S T, Wieman C E 2006 Phys. Rev. Lett. 96 170401
Google Scholar
[7] Marchant A L, Billam T P, Wiles T P, Yu M M H, Gardiner S, Cornish S L 2013 Nat. Commun. 4 1865
Google Scholar
[8] Nguyen J H V, Dyke P, Luo D, Malomed B A, Hulet R G 2014 Nat. Phys. 10 918
Google Scholar
[9] Yefsah T, Sommer A T, Ku M J H, Cheuk L W, Ji W, Bakr W S, Zwierlein M W 2013 Nature 499 426
Google Scholar
[10] Ku M J H, Ji W, Mukherjee B, Guardado-Sanchez E, Cheuk L W, Yefsah T, Zwierlein M W 2014 Phys. Rev. Lett. 113 065301
Google Scholar
[11] 张蔚曦, 张志强, 冉茂武, 欧永康, 何章明 2014 物理学报 63 200507
Google Scholar
Zhang W X, Zhang Z Q, Ran M W, Ou Y K, He Z M 2014 Acta Phys. Sin. 63 200507
Google Scholar
[12] Guo X H, Xu T F, Liu C S 2018 Chin. Rhys. B 27 060307
[13] Wang Q, Wen L, Li Z D 2012 Chin. Phys. B 21 080501
Google Scholar
[14] Lin Y J, Jiménez-GarcÍa K, Spielman I B 2011 Nature 471 83
Google Scholar
[15] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[16] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[17] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[18] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[19] Zhou X, Li Y, Cai Z, Wu C J 2013 J. Phys. B: At. Mol. Opt. Phys. 46 134001
Google Scholar
[20] Xu Y, Zhang Y, Wu B 2013 Phys. Rev. A 87 013614
Google Scholar
[21] Achilleos V, Frantzeskakis D J, Kevrekidis P G, Pelinovsky D E 2013 Phys. Rev. Lett. 110 264101
Google Scholar
[22] Achilleos V, Stockhofe J, Kevrekidis P G, Frantzeskakis D J, Schmelcher P 2013 Europhys. Lett. 103 20002
Google Scholar
[23] Kartashov Y V, Konotop V V, Abdullaev F K 2013 Phys. Rev. Lett. 111 060402
Google Scholar
[24] Liu Y K, Yang S J 2014 Europhys. Lett. 108 30004
Google Scholar
[25] Kartashov Y V, Konotop V V, Zezyulin D A 2014 Phys. Rev. A 90 063621
Google Scholar
[26] Gautam S, Adhikari S K 2015 Laser Phys. Lett. 12 045501
Google Scholar
[27] Gautam S, Adhikari S K 2015 Phys. Rev. A 91 063617
Google Scholar
[28] Zhang Y, Xu Y, Busch T 2015 Phys. Rev. A 91 043629
Google Scholar
[29] Peotta S, Mireles F, Di Ventra M 2015 Phys. Rev. A 91 021601
Google Scholar
[30] Sakaguchi H, Li B, Malomed B A 2014 Phys. Rev. E 89 032920
Google Scholar
[31] Sakaguchi H, Sherman E Y, Malomed B A 2016 Phys. Rev. E 94 032202
Google Scholar
[32] Salasnich L, Cardoso W B, Malomed B A 2014 Phys. Rev. A 90 033629
Google Scholar
[33] Sakaguchi H, Malomed B A 2014 Phys. Rev. E 90 062922
Google Scholar
[34] Lobanov V E, Kartashov Y V, Konotop V V 2014 Phys. Rev. Lett. 112 180403
Google Scholar
[35] Zhang Y C, Zhou Z W, Malomed B A, Pu H 2015 Phys. Rev. Lett. 115 253902
Google Scholar
[36] Beličev P P, Gligorić G, Petrovic J, Maluckov A, Hadžievski L, Malomed B A 2015 J. Phys. B 48 065301
Google Scholar
[37] Li Y, Liu Y, Fan Z, Pang W, Fu S, Malomed B A 2017 Phys. Rev. A 95 063613
Google Scholar
[38] Liao B, Li S, Huang C, Luo Z, Pang W, Tan H, Malomed B A, Li Y 2017 Phys. Rev. A 96 043613
Google Scholar
[39] Sakaguchi H, Malomed B A 2018 Phys. Rev. A 97 013607
Google Scholar
[40] Zhong R, Chen Z, Huang C, Luo Z, Tan H, Malomed B A, Li Y 2018 Front. Phys. 13 130311
Google Scholar
[41] Xu Y, Mao L, Wu B, Zhang C 2014 Phys. Rev. Lett. 113 130404
Google Scholar
[42] Li Y E, Xue J K 2016 Chin. Phys. Lett. 33 100502
Google Scholar
[43] Wen L, Sun Q, Chen Y, Wang D S, Hu J, Chen H, Liu W M, Juzeliūnas G, Malomed B A, Ji A C 2016 Phys. Rev. A 94 061602
Google Scholar
[44] Wen L, Zhang X F, Hu A Y, Zhou J, Yu P, Xia L, Sun Q, Ji A C 2018 Anns. Phys. 390 181
[45] Sakaguchi H, Malomed B A 2017 Phys. Rev. A 96 043620
Google Scholar
[46] Kartashov Y V, Konotop V V 2017 Phys. Rev. Lett. 118 190401
Google Scholar
[47] Wen L, Sun Q, Wang H Q, Ji A C, Liu W M 2012 Phys. Rev. A 86 043602
Google Scholar
[48] Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. Lett. 108 225301
Google Scholar
[49] Gong M, Chen G, Jia S T, Zhang C 2012 Phys. Rev. Lett. 109 105302
Google Scholar
[50] Qu C L, Zheng Z, Gong M, Xu Y, Mao L, Zou X, Guo G, Zhang C 2013 Nat. Commun. 4 2710
Google Scholar
[51] Zhang W, Yi W 2013 Nat. Commun. 4 2711
Google Scholar
[52] Zhao D, Song S W, Wen L, Li Z D, Luo H G, Liu W M 2015 Phys. Rev. A 91 013619
Google Scholar
[53] 宗丰德, 杨阳, 张解放 2009 物理学报 58 3670
Google Scholar
Zong F D, Yang Y, Zhang J F 2009 Acta Phys. Sin. 58 3670
Google Scholar
[54] Alotaibi M O D, Carr L D 2017 Phys. Rev. A 96 013601
Google Scholar
-
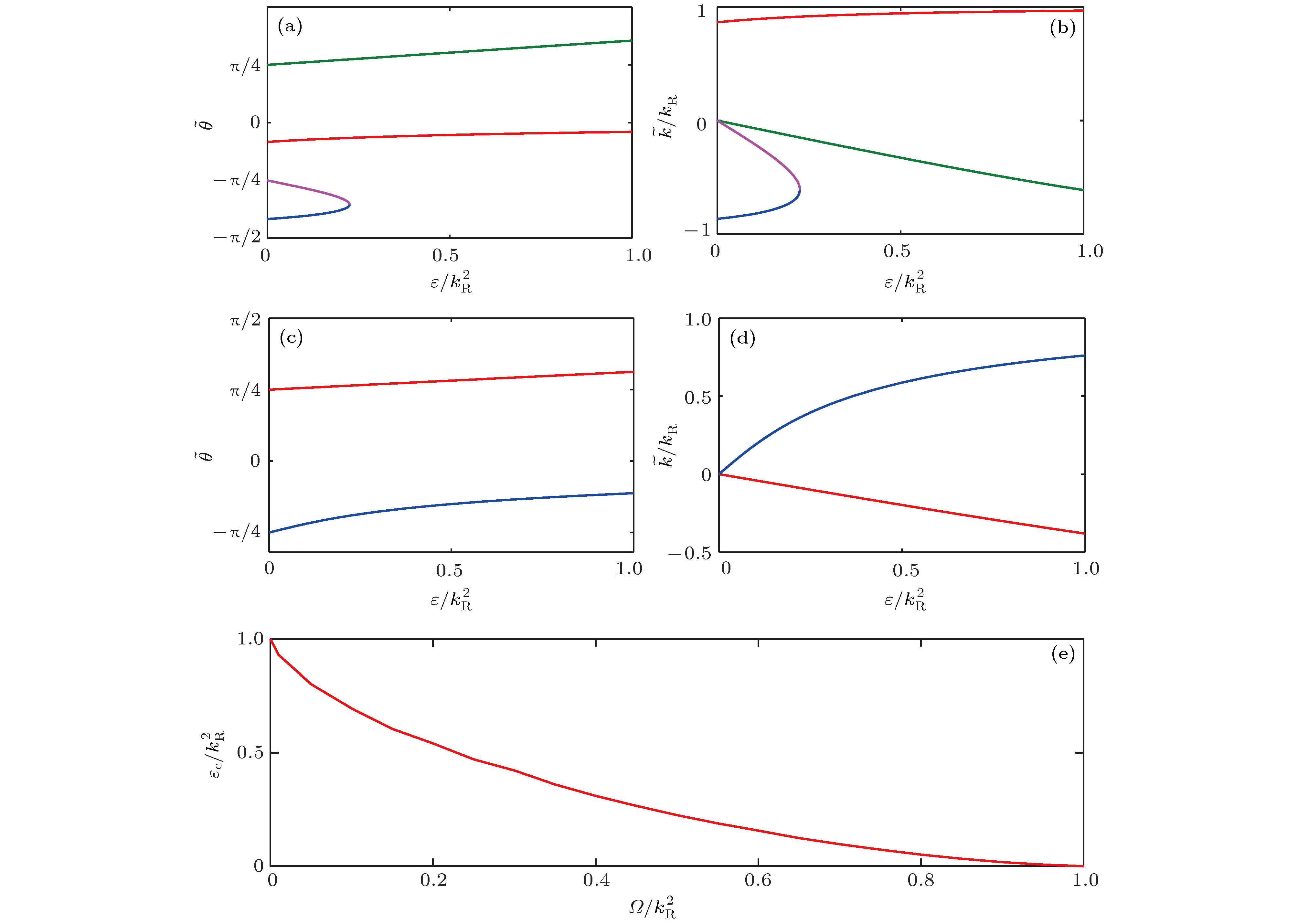
图 1 (a)，(b)
$ \varOmega/k_{\rm R}^2 = 0.5 $ 时固定点解$ \tilde{\theta} $ 和$ \tilde{k} $ 随线性塞曼劈裂$ \varepsilon $ 的变化; (c)，(d)$ \varOmega/k_{\rm R}^2 = 1.5 $ 时固定点解$ \tilde{\theta} $ 和$ \tilde{k} $ 随线性塞曼劈裂$ \varepsilon $ 的变化; (e)$ \varOmega/k_{\rm R}^2<1 $ 时临界值$ \varepsilon_{\rm c}$ 随$ \varOmega $ 的变化Fig. 1. (a) and (b) show the
$ \tilde{\theta} $ and$ \tilde{k} $ change with$ \varepsilon $ for$ \varOmega/k_{\rm R}^2 = 0.5 $ ; (c) and (d) display$ \tilde{\theta} $ and$ \tilde{k} $ change with$ \varepsilon $ for$ \varOmega/k_{\rm R}^2 = 1.5 $ ; (e) shows the critical value$ \varepsilon_{\rm c} $ versus$ \varOmega $ for$ \varOmega/k_{{\rm R}}^2<1 $ .
图 2 (a)和(b)分别展示
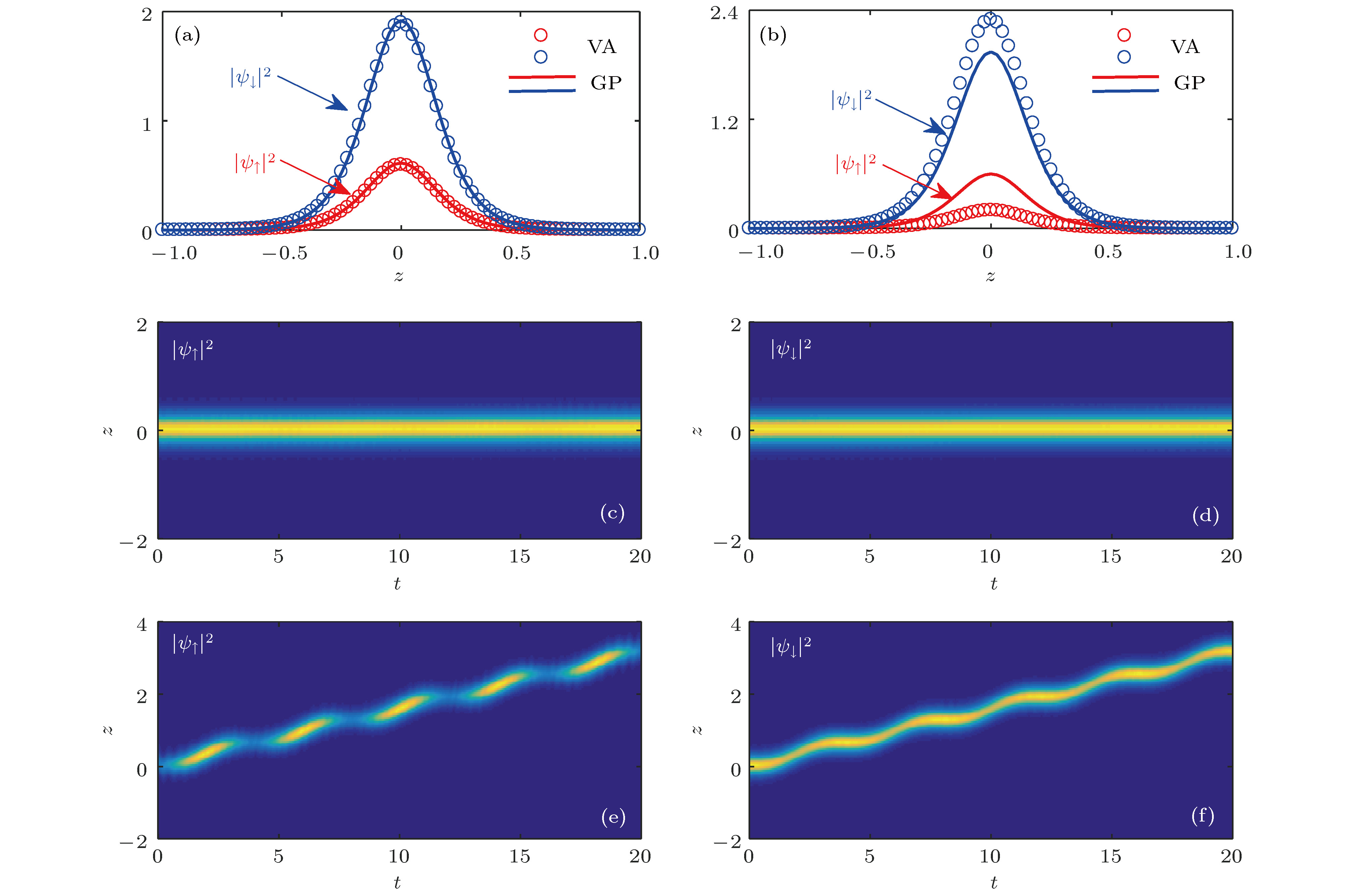
$ k_{\rm R} = 0.2\varOmega $ 和$ k_{\rm R} = 1.5\varOmega $ 时, 变分静态孤子解(圆圈)与GP方程（2）静态孤子的数值解(实线)的对比, 其他参数取值为$ \varepsilon = 0.3 $ ,$ \varOmega = 0.5 $ 及$ g = -10 $ ; (c)—(f)分别为(a)和(b)中的变分静态孤子解作为初始条件在含时GP方程中的动力学演化Fig. 2. (a), (b) show the comparisons between the variationally predicted stationary soliton solutions (circles) and the numerical solutions (solid lines) of stationary solitons of GP equation (2) for
$k_{\rm R}=0.2\varOmega$ and$k_{\rm R}=1.5\varOmega$ with$\varOmega=0.5$ , respectively. The other parameters are$\varepsilon=0.3$ and$g=-10$ ；(c)−(f) are the dynamical evolutions of solitons in time-dependent GP simulations by using the variationally predicted stationary soliton solutions in (a) and (b) as initial wave functions, respectively
图 3
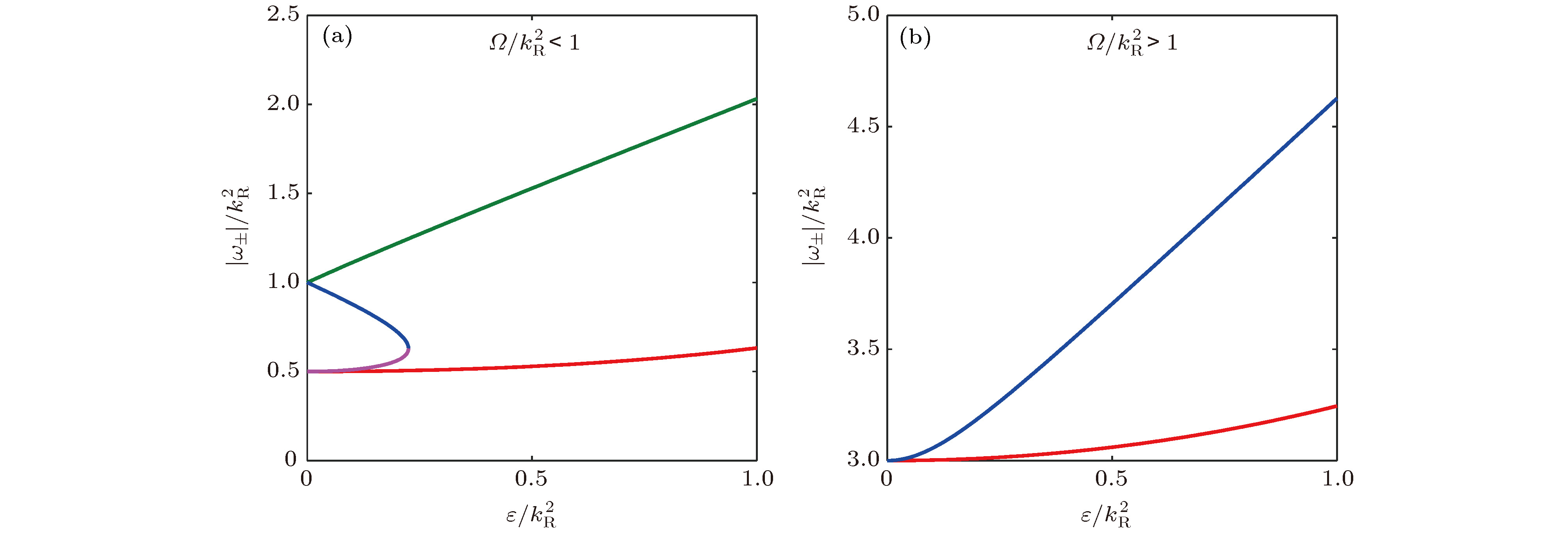
$ \varOmega/k_{\rm R}^2 = 0.5$ (a)和$ \varOmega/k_{\rm R}^2 = 1.5 $ (b)时, 频率$ \omega_{\pm} = \pm 2\varOmega/\sin\left(2\tilde{\theta}\right) $ 随线性塞曼劈裂强度$ \varepsilon $ 的变化Fig. 3. The frequency
$\omega_{\pm}=\pm 2\varOmega/\sin\left(2\tilde{\theta}\right)$ changes with$\varepsilon$ for$\varOmega/k_{\rm R}^2=0.5$ and$\varOmega/k_{\rm R}^2=1.5$ in (a) and (b), respectively.
图 4 (a)—(f)初始值为
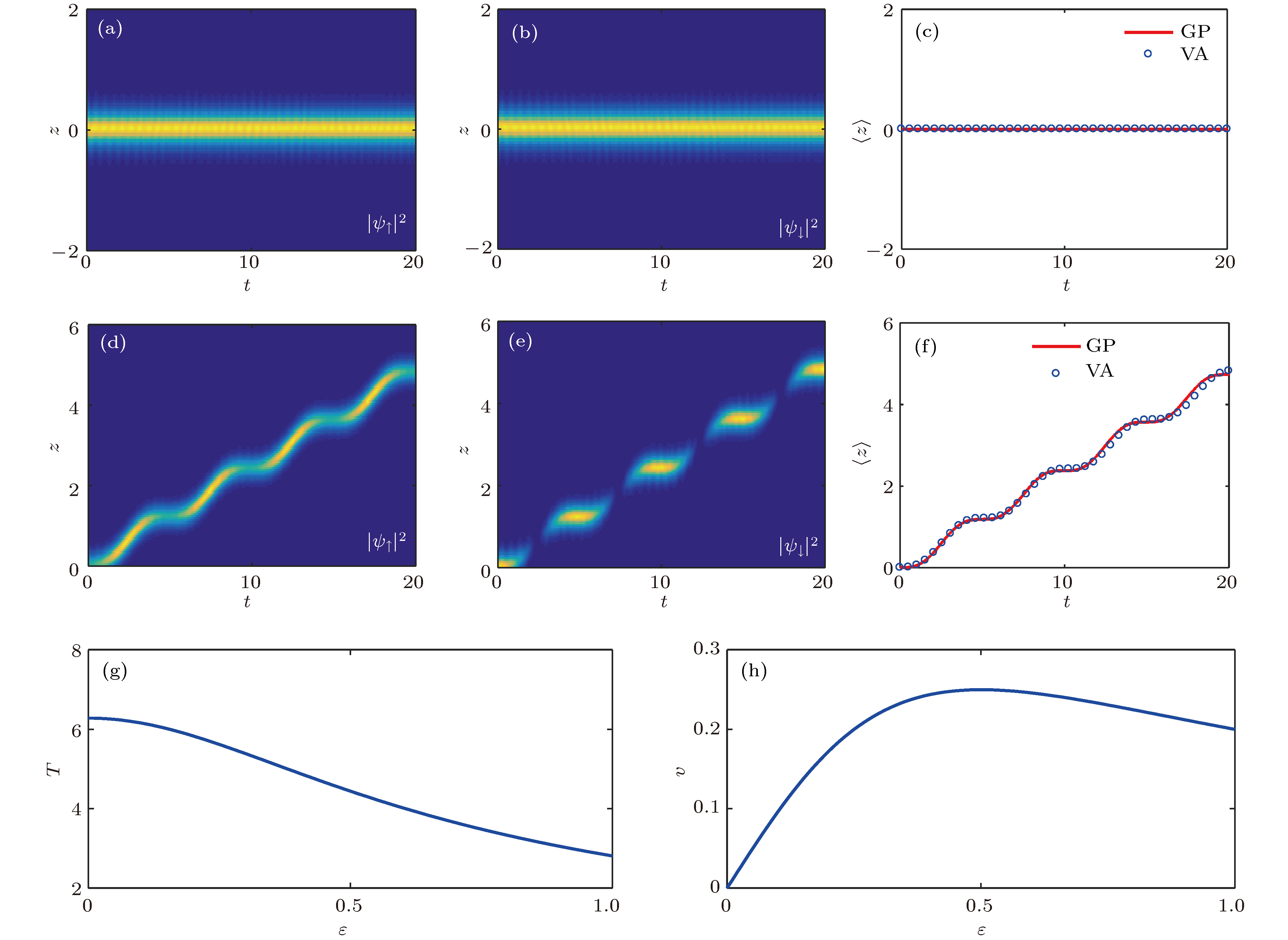
$ \theta_{0} = \dfrac{{\text{π}}}{4} $ ,$ \varphi_{-, 0} = 0 $ 及$ k = 0 $ 的孤子动力学演化 (a)—(c)$ \varepsilon = 0 $ , (d)—(f)$ \varepsilon = 0.35 $ ; 孤子振荡周期$ T(g) $ 及速度$ v(h) $ 随线性塞曼劈裂的变化Fig. 4. (a)−(f) show the dynamical evolutions of initially balanced solitons with
$\theta_0=\dfrac{{\text{π}}}{4}$ ,$k=0$ and$\varphi_{-, 0}=0$ in GP simulations,$\varepsilon=0$ in (a)−(c), and$\varepsilon=0.35$ in (d)−(f); oscillation period$T(g) $ and moving velocity$v(h) $ of solitons change with the linear Zeeman splitting. -
[1] Malomed B A 2006 Soliton Management in Periodic Systems (Vol. 1) (Berlin: Springer) p1
[2] Kevrekidis P G, Frantzeskakis D J, Carretero-Gonzalez R 2008 Emergent Nonlinear Phenomena in Bose-Einstein Condensates (Vol. 1)(Berlin: Springer) pp43−96
[3] Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K, Sanpera A, Shlyapnikov G V, Lewenstein M 1999 Phys. Rev. Lett. 83 5198
Google Scholar
[4] Khaykovich L, Schreck F, Ferrari G, Bourdel T, Cubizolles J, Carr L D, Castin Y, Salomon C 2002 Science 296 1290
Google Scholar
[5] Strecker K E, Partridge G B, Truscott A G, Hulet R G 2002 Nature 417 150
Google Scholar
[6] Cornish S L, Thompson S T, Wieman C E 2006 Phys. Rev. Lett. 96 170401
Google Scholar
[7] Marchant A L, Billam T P, Wiles T P, Yu M M H, Gardiner S, Cornish S L 2013 Nat. Commun. 4 1865
Google Scholar
[8] Nguyen J H V, Dyke P, Luo D, Malomed B A, Hulet R G 2014 Nat. Phys. 10 918
Google Scholar
[9] Yefsah T, Sommer A T, Ku M J H, Cheuk L W, Ji W, Bakr W S, Zwierlein M W 2013 Nature 499 426
Google Scholar
[10] Ku M J H, Ji W, Mukherjee B, Guardado-Sanchez E, Cheuk L W, Yefsah T, Zwierlein M W 2014 Phys. Rev. Lett. 113 065301
Google Scholar
[11] 张蔚曦, 张志强, 冉茂武, 欧永康, 何章明 2014 物理学报 63 200507
Google Scholar
Zhang W X, Zhang Z Q, Ran M W, Ou Y K, He Z M 2014 Acta Phys. Sin. 63 200507
Google Scholar
[12] Guo X H, Xu T F, Liu C S 2018 Chin. Rhys. B 27 060307
[13] Wang Q, Wen L, Li Z D 2012 Chin. Phys. B 21 080501
Google Scholar
[14] Lin Y J, Jiménez-GarcÍa K, Spielman I B 2011 Nature 471 83
Google Scholar
[15] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[16] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[17] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[18] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[19] Zhou X, Li Y, Cai Z, Wu C J 2013 J. Phys. B: At. Mol. Opt. Phys. 46 134001
Google Scholar
[20] Xu Y, Zhang Y, Wu B 2013 Phys. Rev. A 87 013614
Google Scholar
[21] Achilleos V, Frantzeskakis D J, Kevrekidis P G, Pelinovsky D E 2013 Phys. Rev. Lett. 110 264101
Google Scholar
[22] Achilleos V, Stockhofe J, Kevrekidis P G, Frantzeskakis D J, Schmelcher P 2013 Europhys. Lett. 103 20002
Google Scholar
[23] Kartashov Y V, Konotop V V, Abdullaev F K 2013 Phys. Rev. Lett. 111 060402
Google Scholar
[24] Liu Y K, Yang S J 2014 Europhys. Lett. 108 30004
Google Scholar
[25] Kartashov Y V, Konotop V V, Zezyulin D A 2014 Phys. Rev. A 90 063621
Google Scholar
[26] Gautam S, Adhikari S K 2015 Laser Phys. Lett. 12 045501
Google Scholar
[27] Gautam S, Adhikari S K 2015 Phys. Rev. A 91 063617
Google Scholar
[28] Zhang Y, Xu Y, Busch T 2015 Phys. Rev. A 91 043629
Google Scholar
[29] Peotta S, Mireles F, Di Ventra M 2015 Phys. Rev. A 91 021601
Google Scholar
[30] Sakaguchi H, Li B, Malomed B A 2014 Phys. Rev. E 89 032920
Google Scholar
[31] Sakaguchi H, Sherman E Y, Malomed B A 2016 Phys. Rev. E 94 032202
Google Scholar
[32] Salasnich L, Cardoso W B, Malomed B A 2014 Phys. Rev. A 90 033629
Google Scholar
[33] Sakaguchi H, Malomed B A 2014 Phys. Rev. E 90 062922
Google Scholar
[34] Lobanov V E, Kartashov Y V, Konotop V V 2014 Phys. Rev. Lett. 112 180403
Google Scholar
[35] Zhang Y C, Zhou Z W, Malomed B A, Pu H 2015 Phys. Rev. Lett. 115 253902
Google Scholar
[36] Beličev P P, Gligorić G, Petrovic J, Maluckov A, Hadžievski L, Malomed B A 2015 J. Phys. B 48 065301
Google Scholar
[37] Li Y, Liu Y, Fan Z, Pang W, Fu S, Malomed B A 2017 Phys. Rev. A 95 063613
Google Scholar
[38] Liao B, Li S, Huang C, Luo Z, Pang W, Tan H, Malomed B A, Li Y 2017 Phys. Rev. A 96 043613
Google Scholar
[39] Sakaguchi H, Malomed B A 2018 Phys. Rev. A 97 013607
Google Scholar
[40] Zhong R, Chen Z, Huang C, Luo Z, Tan H, Malomed B A, Li Y 2018 Front. Phys. 13 130311
Google Scholar
[41] Xu Y, Mao L, Wu B, Zhang C 2014 Phys. Rev. Lett. 113 130404
Google Scholar
[42] Li Y E, Xue J K 2016 Chin. Phys. Lett. 33 100502
Google Scholar
[43] Wen L, Sun Q, Chen Y, Wang D S, Hu J, Chen H, Liu W M, Juzeliūnas G, Malomed B A, Ji A C 2016 Phys. Rev. A 94 061602
Google Scholar
[44] Wen L, Zhang X F, Hu A Y, Zhou J, Yu P, Xia L, Sun Q, Ji A C 2018 Anns. Phys. 390 181
[45] Sakaguchi H, Malomed B A 2017 Phys. Rev. A 96 043620
Google Scholar
[46] Kartashov Y V, Konotop V V 2017 Phys. Rev. Lett. 118 190401
Google Scholar
[47] Wen L, Sun Q, Wang H Q, Ji A C, Liu W M 2012 Phys. Rev. A 86 043602
Google Scholar
[48] Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. Lett. 108 225301
Google Scholar
[49] Gong M, Chen G, Jia S T, Zhang C 2012 Phys. Rev. Lett. 109 105302
Google Scholar
[50] Qu C L, Zheng Z, Gong M, Xu Y, Mao L, Zou X, Guo G, Zhang C 2013 Nat. Commun. 4 2710
Google Scholar
[51] Zhang W, Yi W 2013 Nat. Commun. 4 2711
Google Scholar
[52] Zhao D, Song S W, Wen L, Li Z D, Luo H G, Liu W M 2015 Phys. Rev. A 91 013619
Google Scholar
[53] 宗丰德, 杨阳, 张解放 2009 物理学报 58 3670
Google Scholar
Zong F D, Yang Y, Zhang J F 2009 Acta Phys. Sin. 58 3670
Google Scholar
[54] Alotaibi M O D, Carr L D 2017 Phys. Rev. A 96 013601
Google Scholar
下载:
计量
- 文章访问数: 10076
- PDF下载量: 144
- 被引次数: 0
