-
The existence of robust conducting edge states is one of the most prominent properties of topological insulator, which is often simply illustrated as a consequence of bulk-boundary correspondence. Then here arises a new question whether similar robust edge states appear in some other topological-trivial systems, or rather, given a general answer of fundamental mathematics such as harmonic analysis or K-theory to this problem, we study one-dimensional two-tile lattices and show that the robust edge states can exist in topological-trivial complex lattices. Under the tight-binding approximation, all kinds of one-dimensional two-tile lattices with staggered hopping matrix elements can be described by the Su-Schrieffer-Heeger model or the Rice-Mele model, depending on their site energy. The site energy values of the Su-Schrieffer-Heeger model are equal, and often assumed to be zero, and the Rice-Mele model is constructed to describe the one-dimensional two-tile lattices having two different site energy values. With the help of the generalized Bloch theorem, the eigen-state problem of electrons in one-dimensional two-tile complex lattices are solved systematically, and the analytical expressions for the wavefunctions of the edge states in the corresponding finite lattice are obtained. The numerical and analytical results show that the edge states can also emerge in any of one-dimensional two-tile lattices beyond the Su-Schrieffer-Heeger lattice, i.e., provided that the magnitude of intracell hopping is less than the intercell hopping, a pair of edge states can also emerge in Rice-Mele lattice. Unlike the Su-Schrieffer-Heeger edge states, the two Rice-Mele edge states are locally distributed at one end of the finite lattice: one at the left and another one at right. The Zak phase is a topological invariant of the Su-Schrieffer-Heeger model, but it is no longer invariant for the Rice-Mele model because of the breaking of spatial inversion symmetry, and therefore the Rice-Mele lattices are topologically trivial. However, the Rice-Mele edge states are also robust to the non-diagonal disorder of the lattice. In addition, it is proven that the winding number can provide a general criterion for the existence of a couple of edge states in any one-dimensional two-tile lattice whether it is the Su-Schrieffer-Heeger lattice or not. These results lead to a conclusion that the topological invariant is not necessary for the robust edge states to occur.
-
Keywords:
- topological insulator /
- edge state /
- winding number
[1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J 1983 Phys. Rev. B 27 6083
Google Scholar
[3] Berry M V 1984 Proc. R. Soc. Lond. 392 45
[4] Thouless D J, Kohmoto M, Nightingale M P, Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[5] Niu Q, Thouless D J 1984 J. Phys. A 17 2453
Google Scholar
[6] Kohmoto M 1985 Ann. Phys. 160 343
Google Scholar
[7] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[8] Niu Q 1986 Phys. Rev. B 34 5073
Google Scholar
[9] Niu Q, Thouless D J, Wu Y S 1985 Phys. Rev. B 31 3372
Google Scholar
[10] Simon B 1983 Phys. Rev. Lett. 51 2167
Google Scholar
[11] Zak J 1989 Phys. Rev. Lett. 62 2747
Google Scholar
[12] Haldane F D M 2004 Phys. Rev. Lett. 93 206602
Google Scholar
[13] Murakami S, Nagaosa N, Zhang S C 2004 Phys. Rev. Lett. 93 156804
Google Scholar
[14] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[15] Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757
Google Scholar
[16] Moore J E 2010 Nature 464 194
Google Scholar
[17] Xiao D, Chang M C, Niu Q 2010 Rev. Mod. Phys. 82 1959
Google Scholar
[18] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[19] Nagaosa N, Tokura Y 2013 Nature Nano 8 899
Google Scholar
[20] Shen S Q 2012 Topological Insulators (Berlin: Springer) pp81−86
[21] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press) pp6−14
[22] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp16−22
[23] Guo H M 2016 Sci. China: Phys. Mech. Astron. 59 637401
[24] Prodan E, Schulz-Baldes H 2016 Bulk and Boundary Invariants for Complex Topological Insulators: From K-Theory to Physics (Switzerland: Springer International Publishing) pp85−111
[25] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
[26] Rice M L, Mele E J 1982 Phys. Rev. Lett. 49 1455
Google Scholar
[27] RhimJ-W, Behrends J, Bardarson J H 2017 Phys. Rev. B 95 035421
Google Scholar
[28] 邓伟胤, 朱瑞, 邓文基 2013 物理学报 62 067301
Google Scholar
Deng W Y, Zhu R, Deng W J 2013 Acta Phys. Sin. 62 067301
Google Scholar
-
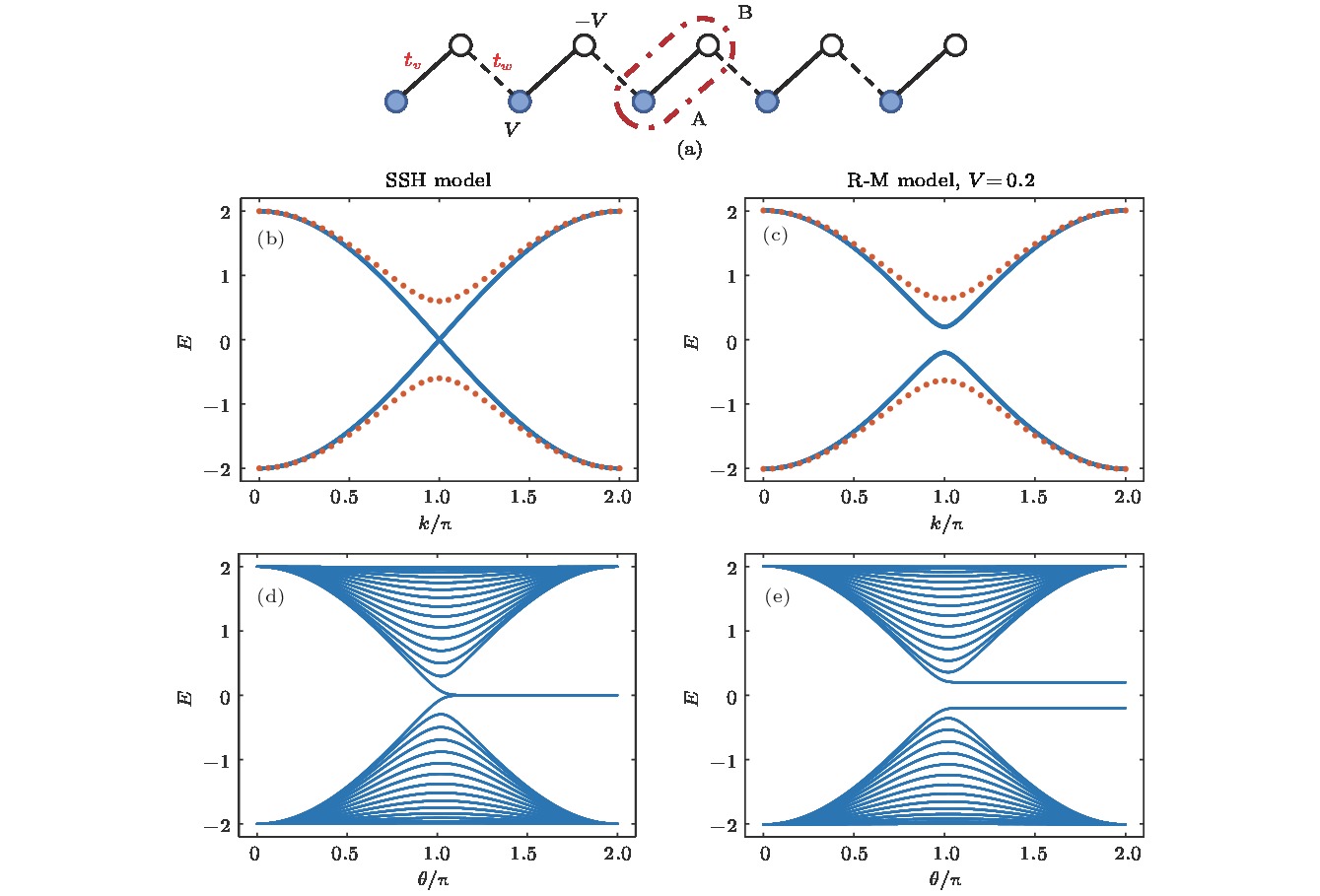
图 1 (a) R-M紧束缚模型,
${t_v}$ 和${t_w}$ 分别表示原胞内和原胞间电子的跃迁矩阵元; (b), (c)分别为无限SSH晶格和R-M晶格的电子能谱; 蓝色实线和红色点线分别取${t_v} = {t_w} = 1$ 和${t_v} = 0.8$ ,${t_w} = 1.2$ , R-M晶格$V = 0.2$ ; (d), (e)分别展示包含15个原胞的有限SSH晶格和R-M晶格的能量本征值随跃迁矩阵元的变化,${t_v} = 1 + \cos \theta $ ,${t_w} = 1 - \cos \theta $ ; 当${t_v} < {t_w}$ 时, 两者都涌现出一对边缘态Fig. 1. (a) Schematic diagram of tight-bonding R-M model,
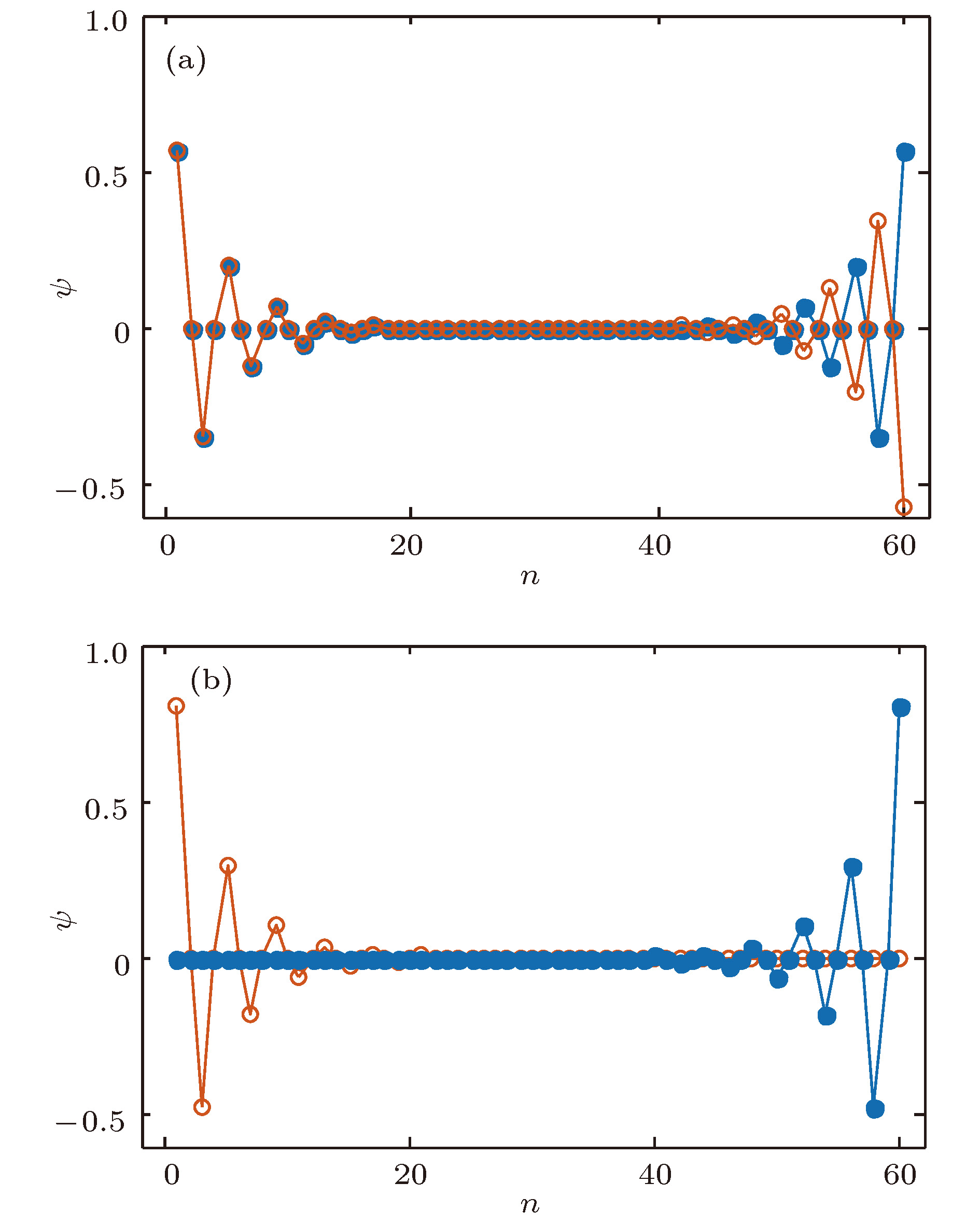
${t_v}$ and${t_w}$ denote the intracellular and intercellular hopping elements, respectively; (b) and (c) are energy spectrum of electron in infinite SSH model and R-M model, where the solid blue lines are drawn for${t_v} = \;{t_w} = 1$ , and the red dot line for${t_v} = 0.8$ ,${t_w} = 1.2$ , and$V = 0.2$ for R-M model; (d) and (e) shown the eigen energies of electron in finite (15 cells) SSH lattice and R-M lattice varying with the hopping elements,${t_v} = 1 + \cos \theta $ ,${t_w} = 1 - \cos \theta $ ; for both of them, a couple of edge states emerge when${t_v} < {t_w}$ .
图 2 一维二元有限晶格的边缘态(其中30个原胞数包含60个格点, 参数取
$\theta \; = \;0.58{\text{π}}$ , 即${t_v} = 0.75,$ ${t_w} = 1.25$ )(a)有限SSH晶格$V = 0$ , 两个边缘态都同时出现在晶格的两端, 它们的本征能量都逼近于零; (b) 有限R-M晶格$V=0.2$ , 红色空心圆和蓝色实心圆点分别表示逼近上能带底和下能带顶两个边缘态, 分别局域在晶格的左右端Fig. 2. Edge states of electron in one-dimensional two-tile finite lattice; the parameters are taken as 30 cells (60 atoms),
$\theta \; = \;0.58{\text{π}}$ , i.e.${t_v} = 0.75,$ ${t_w} = 1.25$ : (a)$V = \;0$ for SSH lattice, the eigen-energy values of the two edge states approach to zero, and each of the edge states appears at two ends of the lattice; (b)$V = 0.2$ for R-M lattice, the red hollow circles stand for the edge state near the upper band, the blue solid dot for the edge state near the lower band; one of them is localized at the left end, and the other at the right end.
图 3 一维二元晶格的Zak相位随跃迁矩阵元的变化, 其中红线表示SSH模型的Zak相位, 且
${\gamma _ + } = {\gamma _ - }$ ; 黑色实线和虚线分别是R-M晶格($V = 0.2$ )上下能级的Zak相位${\gamma _ + }$ 和${\gamma _ - }$ Fig. 3. Zak phases variation with the hopping elements and site energy. The red line presents the Zak phase for SSH model, and
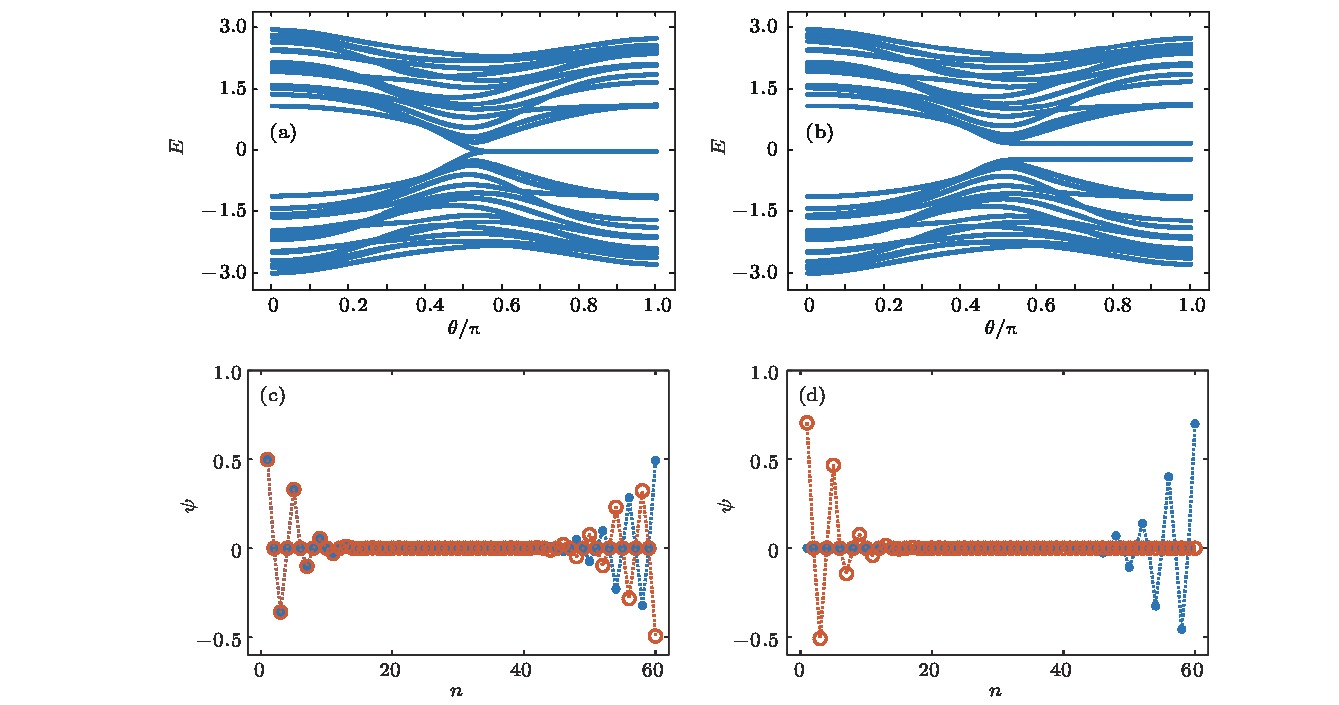
${\gamma _ + } = {\gamma _ - }$ . For the R-M lattice with$V = 0.2$ , the black solid line and dotted line show${\gamma _ + }$ and${\gamma _ - }$ , respectively.
图 4 非对角无序对能谱和边缘态的影响(非对角无序的幅度为
$\xi = 0.5$ , 跃迁矩阵元${t_v} = 0.75$ ,${t_w} = 1.25$ ) (a), (b)分别是包含15个原胞的有限SSH晶格和R-M晶格的能谱; (c), (d)分别是包含30个原胞的有限SSH晶格和R-M晶格的边缘态Fig. 4. Effects of non-diagonal disorder on the energy spectrum and the edge states. The strength of the off-diagonal disorder is taken of
$\xi \; = \;{\rm{0.5}}$ , hopping elements${t_v} = 0.75$ ,${t_w} = 1.25$ . Panels (a) and (b) present the spectrums of finite SSH lattice and R-M lattice consist of 15 unit cells, respectively; (c) and (d) show the edge states of electron in the finite SSH lattice and the R-M lattice of 30 unit cells. -
[1] Klitzing K V, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Thouless D J 1983 Phys. Rev. B 27 6083
Google Scholar
[3] Berry M V 1984 Proc. R. Soc. Lond. 392 45
[4] Thouless D J, Kohmoto M, Nightingale M P, Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[5] Niu Q, Thouless D J 1984 J. Phys. A 17 2453
Google Scholar
[6] Kohmoto M 1985 Ann. Phys. 160 343
Google Scholar
[7] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[8] Niu Q 1986 Phys. Rev. B 34 5073
Google Scholar
[9] Niu Q, Thouless D J, Wu Y S 1985 Phys. Rev. B 31 3372
Google Scholar
[10] Simon B 1983 Phys. Rev. Lett. 51 2167
Google Scholar
[11] Zak J 1989 Phys. Rev. Lett. 62 2747
Google Scholar
[12] Haldane F D M 2004 Phys. Rev. Lett. 93 206602
Google Scholar
[13] Murakami S, Nagaosa N, Zhang S C 2004 Phys. Rev. Lett. 93 156804
Google Scholar
[14] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[15] Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757
Google Scholar
[16] Moore J E 2010 Nature 464 194
Google Scholar
[17] Xiao D, Chang M C, Niu Q 2010 Rev. Mod. Phys. 82 1959
Google Scholar
[18] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[19] Nagaosa N, Tokura Y 2013 Nature Nano 8 899
Google Scholar
[20] Shen S Q 2012 Topological Insulators (Berlin: Springer) pp81−86
[21] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press) pp6−14
[22] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp16−22
[23] Guo H M 2016 Sci. China: Phys. Mech. Astron. 59 637401
[24] Prodan E, Schulz-Baldes H 2016 Bulk and Boundary Invariants for Complex Topological Insulators: From K-Theory to Physics (Switzerland: Springer International Publishing) pp85−111
[25] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
[26] Rice M L, Mele E J 1982 Phys. Rev. Lett. 49 1455
Google Scholar
[27] RhimJ-W, Behrends J, Bardarson J H 2017 Phys. Rev. B 95 035421
Google Scholar
[28] 邓伟胤, 朱瑞, 邓文基 2013 物理学报 62 067301
Google Scholar
Deng W Y, Zhu R, Deng W J 2013 Acta Phys. Sin. 62 067301
Google Scholar
下载:
计量
- 文章访问数: 10310
- PDF下载量: 372
- 被引次数: 0
