-
从物理学的视角看, 群体观点演化实质可以看作是观点粒子状态变化的集体效应. 本文考察在双稳态势中噪声诱导观点粒子的状态转变, 利用加权拉盖尔完备正交函数法计算了时间关联函数和描述驱动-响应关系的弛豫时间. 理论计算结果表明, 噪声诱导作用存在一个临界值Dc, 若噪声强度高于临界值, 时间关联函数随关联时间呈指数型增加. 结果还显示, 存在弛豫时间随势垒纵横比/噪声强度变化取值趋于无穷的双奇异点现象. 奇异点处无法实现观点粒子状态的转变. 弛豫时间与势垒纵横比之间存在线性关系, 预示着在双稳态势场中观点粒子受噪声驱动呈现类似牛顿第二定律的驱动-响应关系, 而弛豫时间在这个关系中充当表征惯性质量的角色.From the perspective of physics, evolution of group opinion can be regarded as the collective effect of the state change of opinion particles. It is similar to a material particle system that there is usually a dynamic criticality in the opinion state transition of a group, and is dominated by a scaling law. To exhibit this phenomenon, a bistable potential field is introduced to mimic the opinion transition by the jump from one stable state to the other. In this investigation, we will focus on the state change of the opinion particles induced by the noise. The time correlation function and the relaxation time describing drive-response relationship are calculated, by using of the generalized Laguerre weight complete set of orthogonal functions method, to reveal the regularity and the relative mechanism governing the state change of the opinion particle confined by the bistable potential and affected by the noise. The results indicate that there is a critical value Dc for noise intensity. When the noise intensity is greater than Dc, the time correlation function will increase exponentially with correlation time τ. There also are two points at which the dependence of the relaxation time on the noise intensity/aspect ratio of the energy barrier are divergent. The divergence implies that the state transition of opinion particles cannot be achieved. It is worth noting that there is a linear relationship between the relaxation time and the aspect ratio of energy barrier. This relation means that there is a drive-response relationship for opinion particles in the bistable potential field just like the Newton’s second law, in which the time relaxation plays the role of quasi-inertia. This result also implies another important conclusion that the energy and information may be equated due to the fact that the opinion particle transiting from one stable state to the other needs obtaining energy to climb over the barrier, and from another point of view, the transition can be regarded as the opinion particle having been obtaining information via the noise correlation. These investigations may provide us with new understandings to the evolution of group opinion.
-
Keywords:
- opinion space /
- Laguerre function /
- relaxation time /
- drive-response relationship
[1] Wang P, Song J, Huo J, Hao R, Wang X M 2017 Int. J. Mod. Phys. C 28 1750135
 Google Scholar
Google Scholar
[2] 刘巧玲, 李劲, 肖人斌 2017 计算机应用 37 1419
 Google Scholar
Google Scholar
Liu Q L, Li J, Xiao R B 2017 J. Comp. Appl. 37 1419
 Google Scholar
Google Scholar
[3] Ding Z J, Sun X Y, Wang B H 2012 Proc. Eng. 31 1072
 Google Scholar
Google Scholar
[4] Weidlich W 1971 Br. J. Math. Statist. Psychol. 24 251
 Google Scholar
Google Scholar
[5] Galam S, Gefen Y, Shapir Y 1982 J. Math. Sociol. 9 1
 Google Scholar
Google Scholar
[6] Galam S, Moscovici S 1991 Eur. J. Soc. Psychol. 21 49
 Google Scholar
Google Scholar
[7] Axelrod R 1997 J. Confl. Resolut. 41 203
 Google Scholar
Google Scholar
[8] Wichmann S 2008 Lang. Linguist. Compass. 2 442
 Google Scholar
Google Scholar
[9] Helbing D 2001 Rev. Mod. Phys. 73 1067
 Google Scholar
Google Scholar
[10] Newman M E J 2002 Phys. Rev. E 66 035101
[11] 封晨洁, 王鹏, 王旭明 2015 物理学报 64 030502
 Google Scholar
Google Scholar
Feng C J, Wang P, Wang X M 2015 Acta Phys. Sin. 64 030502
 Google Scholar
Google Scholar
[12] Wang P, Pan F C, Huo J, Wang X M 2019 arXiv:1909.04220
[13] Wang P, Pan F C, Huo J, Wang X M 2019 arXiv:1909.04208
[14] Helbing D, Molnár P 1995 Phys. Rev. E 51 4282
 Google Scholar
Google Scholar
[15] Helbing D 1994 J. Math. Sociol. 19 189
 Google Scholar
Google Scholar
[16] Helbing D, Farkas I, Vicsek T 2000 Nature 407 487
 Google Scholar
Google Scholar
[17] Castellano C, Marsili M, Vespignani A 2000 Phys. Rev. Lett. 85 3536
 Google Scholar
Google Scholar
[18] Sznajd-Weron K, Sznajd J 2000 Int. J. Mod. Phys. C 11 1157
 Google Scholar
Google Scholar
[19] Stauffer D, Sousa A O, de Oliveira S M 2000 Int. J. Mod. Phys. C 11 1239
 Google Scholar
Google Scholar
[20] Sznajd-Weron K, Weron R 2002 Int. J. Mod. Phys. C 13 115
 Google Scholar
Google Scholar
[21] Sznajd-Weron K, Sznajd J 2005 Physica A 351 593
 Google Scholar
Google Scholar
[22] Comincioli V, Della Croce L, Toscani G 2009 Kin. Rel. Mod. 2 135
 Google Scholar
Google Scholar
[23] Galam S 2005 Phys. Rev. E 71 046123
 Google Scholar
Google Scholar
[24] Kimizuka M, Munakata T, Rosinberg M L 2010 Phys. Rev. E 82 041129
 Google Scholar
Google Scholar
[25] Nyczka P, Cisło J, Sznajd-Weron K 2012 Physica A 391 317
 Google Scholar
Google Scholar
[26] de la Lama M S, Szendro I G, Iglesias J R, Wio H S 2006 European. Phys. J. B 51 435
[27] Risken H 1984 The Fokker-Planck Equation: Methods of Solution and Applications (2nd Ed.) (New York: Springer-Verlag Berlin Heidelberg) pp196−275
[28] Graham R, Schenzle A 1982 Phys. Rev. A 26 1676
 Google Scholar
Google Scholar
[29] Huber D, Tsimring L S 2003 Phys. Rev. Lett. 91 260601
 Google Scholar
Google Scholar
[30] Lett P, Short R, Mandel L 1984 Phys. Rev. Lett. 52 341
 Google Scholar
Google Scholar
[31] Sancho J M, San Miguel M, Katz S L, Gunton J D 1982 Phys. Rev. A 26 1589
 Google Scholar
Google Scholar
[32] Landauer R 1961 IBM J. Res. Dev. 5 183
 Google Scholar
Google Scholar
[33] Bennett C H 1982 Int. J. Theor. Phys. 21 905
 Google Scholar
Google Scholar
[34] Dahlsten O C O 2013 Entropy 15 5346
 Google Scholar
Google Scholar
-
图 2 在确定势垒高度的纵横比(
$\gamma =0.2$ )情形下, 时间关联函数对关联时间长度的依赖关系 (a) 若噪声强度$D < {D_{\rm{c}}}$ , 关联函数呈单峰形式, 当$D\to D_c$ , 时间关联函数至时间关联长度$\tau =2.4$ 时达到确定值$ {\varPhi _x}(\tau \geqslant 2.4) \to 1.3$ ; (b) 若噪声强度$D>{D_{\rm{c}}}$ , 时间关联函数对关联时间长度呈指数关系,$ {\varPhi _x}(\tau ) \propto {{\rm{e}}^{ - {k_{\rm{e}}}\tau }} $ Fig. 2. Time correlation function with different aspect ratios of energy barrier: (a) When
$D<{D_{\rm{c}}}$ , the correlation function presents single peak; when$D \to {D_{\rm{c}}}$ and time correlation length$\tau=2.4$ , the time correlation function tends to 1.3; (b) when$D>{D_{\rm{c}}}$ , time correlation function increases with time correlation length exponentially,${\varPhi _x}(\tau ) \propto {{\rm{e}}^{ - {k_{\rm{e}}}\tau }}$ .图 4 蓝色点连成的线为
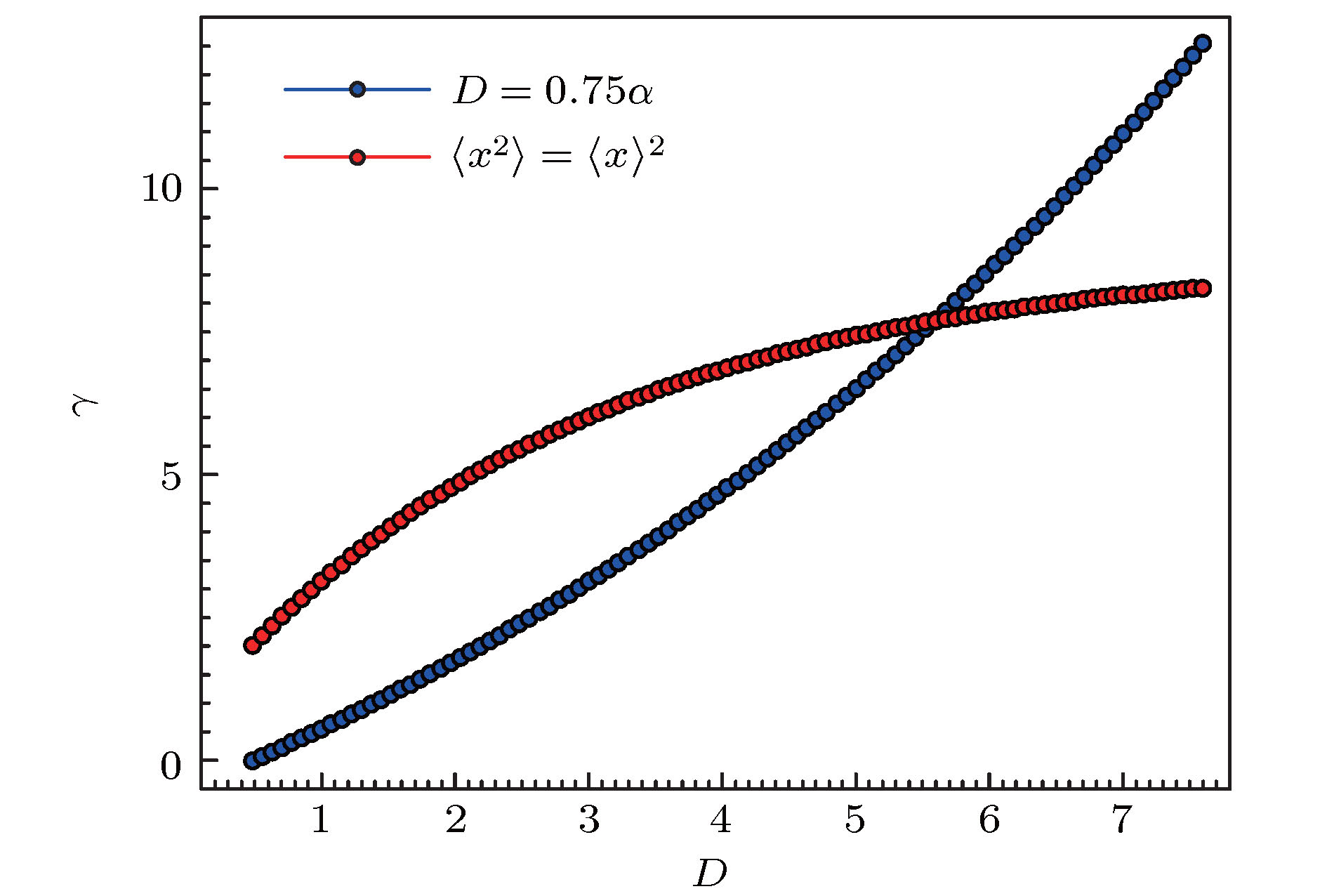
$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{{\gamma _{\rm{s}}} = \frac{2}{3}\sqrt {D_{\rm{s}}^3/3} }}} \right\}$ , 红色圈连成的线表示临界条件$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{\langle {{x^2}} \rangle - {{\langle x \rangle }^2} = 0}}} \right\}$ Fig. 4. Dotted blue line shows the critical condition of
$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{{\gamma _{\rm{s}}} = \frac{2}{3}\sqrt {D_{\rm{s}}^3/3} }}} \right\}$ , red circle line presents the critical condition$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{\langle {{x^2}} \rangle - {{\langle x \rangle }^2} = 0}}} \right\}$ . -
[1] Wang P, Song J, Huo J, Hao R, Wang X M 2017 Int. J. Mod. Phys. C 28 1750135
 Google Scholar
Google Scholar
[2] 刘巧玲, 李劲, 肖人斌 2017 计算机应用 37 1419
 Google Scholar
Google Scholar
Liu Q L, Li J, Xiao R B 2017 J. Comp. Appl. 37 1419
 Google Scholar
Google Scholar
[3] Ding Z J, Sun X Y, Wang B H 2012 Proc. Eng. 31 1072
 Google Scholar
Google Scholar
[4] Weidlich W 1971 Br. J. Math. Statist. Psychol. 24 251
 Google Scholar
Google Scholar
[5] Galam S, Gefen Y, Shapir Y 1982 J. Math. Sociol. 9 1
 Google Scholar
Google Scholar
[6] Galam S, Moscovici S 1991 Eur. J. Soc. Psychol. 21 49
 Google Scholar
Google Scholar
[7] Axelrod R 1997 J. Confl. Resolut. 41 203
 Google Scholar
Google Scholar
[8] Wichmann S 2008 Lang. Linguist. Compass. 2 442
 Google Scholar
Google Scholar
[9] Helbing D 2001 Rev. Mod. Phys. 73 1067
 Google Scholar
Google Scholar
[10] Newman M E J 2002 Phys. Rev. E 66 035101
[11] 封晨洁, 王鹏, 王旭明 2015 物理学报 64 030502
 Google Scholar
Google Scholar
Feng C J, Wang P, Wang X M 2015 Acta Phys. Sin. 64 030502
 Google Scholar
Google Scholar
[12] Wang P, Pan F C, Huo J, Wang X M 2019 arXiv:1909.04220
[13] Wang P, Pan F C, Huo J, Wang X M 2019 arXiv:1909.04208
[14] Helbing D, Molnár P 1995 Phys. Rev. E 51 4282
 Google Scholar
Google Scholar
[15] Helbing D 1994 J. Math. Sociol. 19 189
 Google Scholar
Google Scholar
[16] Helbing D, Farkas I, Vicsek T 2000 Nature 407 487
 Google Scholar
Google Scholar
[17] Castellano C, Marsili M, Vespignani A 2000 Phys. Rev. Lett. 85 3536
 Google Scholar
Google Scholar
[18] Sznajd-Weron K, Sznajd J 2000 Int. J. Mod. Phys. C 11 1157
 Google Scholar
Google Scholar
[19] Stauffer D, Sousa A O, de Oliveira S M 2000 Int. J. Mod. Phys. C 11 1239
 Google Scholar
Google Scholar
[20] Sznajd-Weron K, Weron R 2002 Int. J. Mod. Phys. C 13 115
 Google Scholar
Google Scholar
[21] Sznajd-Weron K, Sznajd J 2005 Physica A 351 593
 Google Scholar
Google Scholar
[22] Comincioli V, Della Croce L, Toscani G 2009 Kin. Rel. Mod. 2 135
 Google Scholar
Google Scholar
[23] Galam S 2005 Phys. Rev. E 71 046123
 Google Scholar
Google Scholar
[24] Kimizuka M, Munakata T, Rosinberg M L 2010 Phys. Rev. E 82 041129
 Google Scholar
Google Scholar
[25] Nyczka P, Cisło J, Sznajd-Weron K 2012 Physica A 391 317
 Google Scholar
Google Scholar
[26] de la Lama M S, Szendro I G, Iglesias J R, Wio H S 2006 European. Phys. J. B 51 435
[27] Risken H 1984 The Fokker-Planck Equation: Methods of Solution and Applications (2nd Ed.) (New York: Springer-Verlag Berlin Heidelberg) pp196−275
[28] Graham R, Schenzle A 1982 Phys. Rev. A 26 1676
 Google Scholar
Google Scholar
[29] Huber D, Tsimring L S 2003 Phys. Rev. Lett. 91 260601
 Google Scholar
Google Scholar
[30] Lett P, Short R, Mandel L 1984 Phys. Rev. Lett. 52 341
 Google Scholar
Google Scholar
[31] Sancho J M, San Miguel M, Katz S L, Gunton J D 1982 Phys. Rev. A 26 1589
 Google Scholar
Google Scholar
[32] Landauer R 1961 IBM J. Res. Dev. 5 183
 Google Scholar
Google Scholar
[33] Bennett C H 1982 Int. J. Theor. Phys. 21 905
 Google Scholar
Google Scholar
[34] Dahlsten O C O 2013 Entropy 15 5346
 Google Scholar
Google Scholar
计量
- 文章访问数: 12778
- PDF下载量: 134
- 被引次数: 0













 下载:
下载: