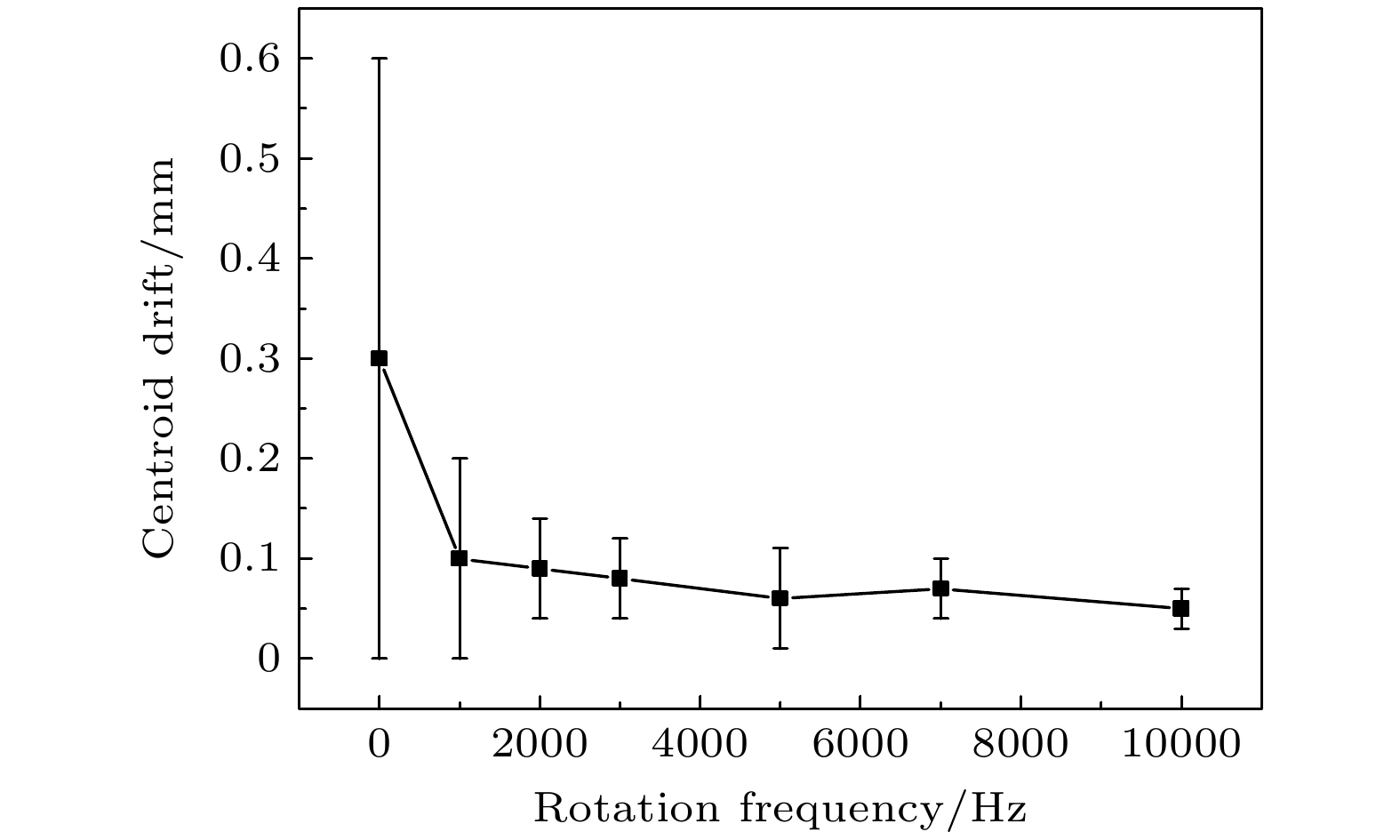
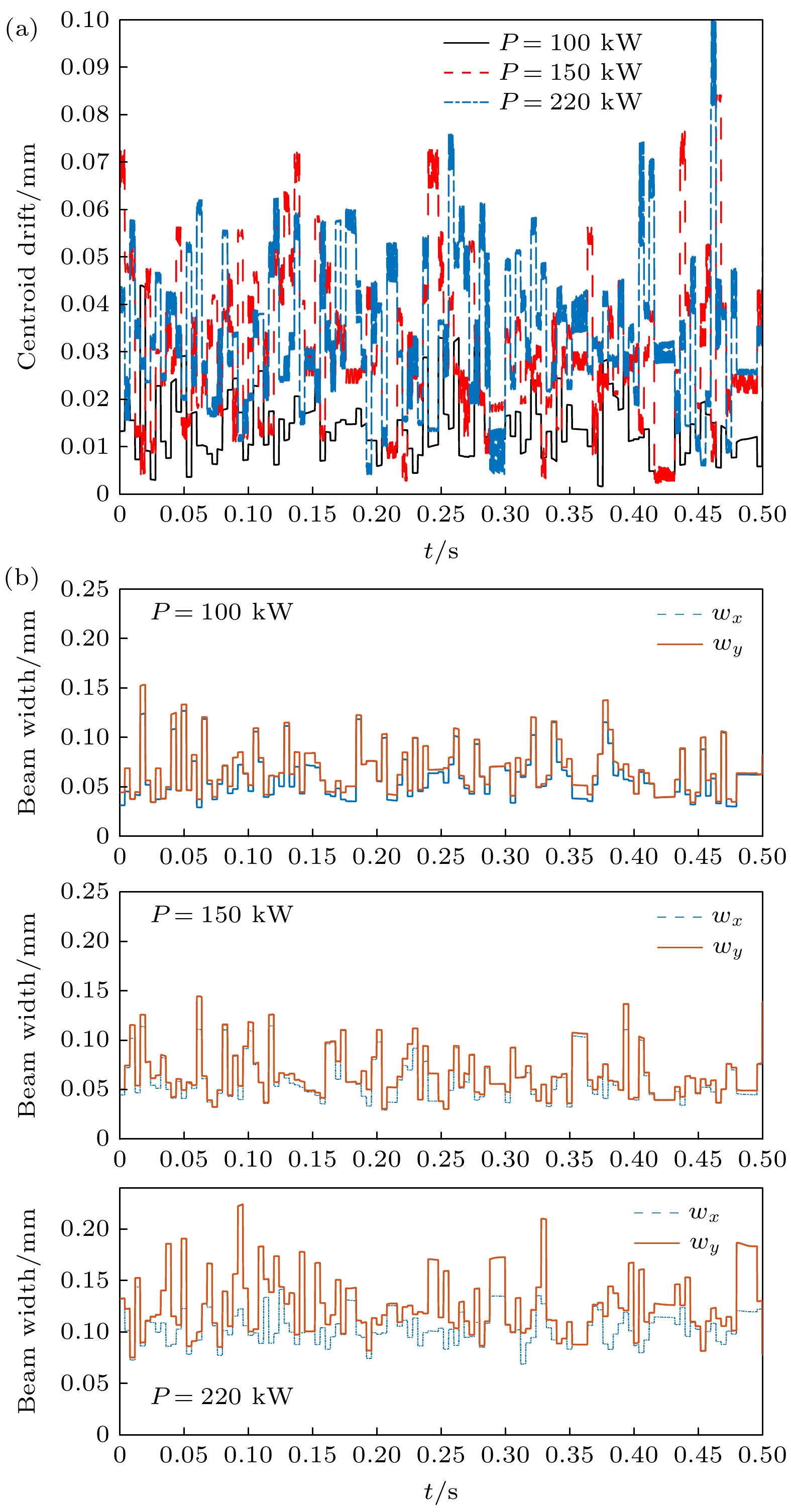
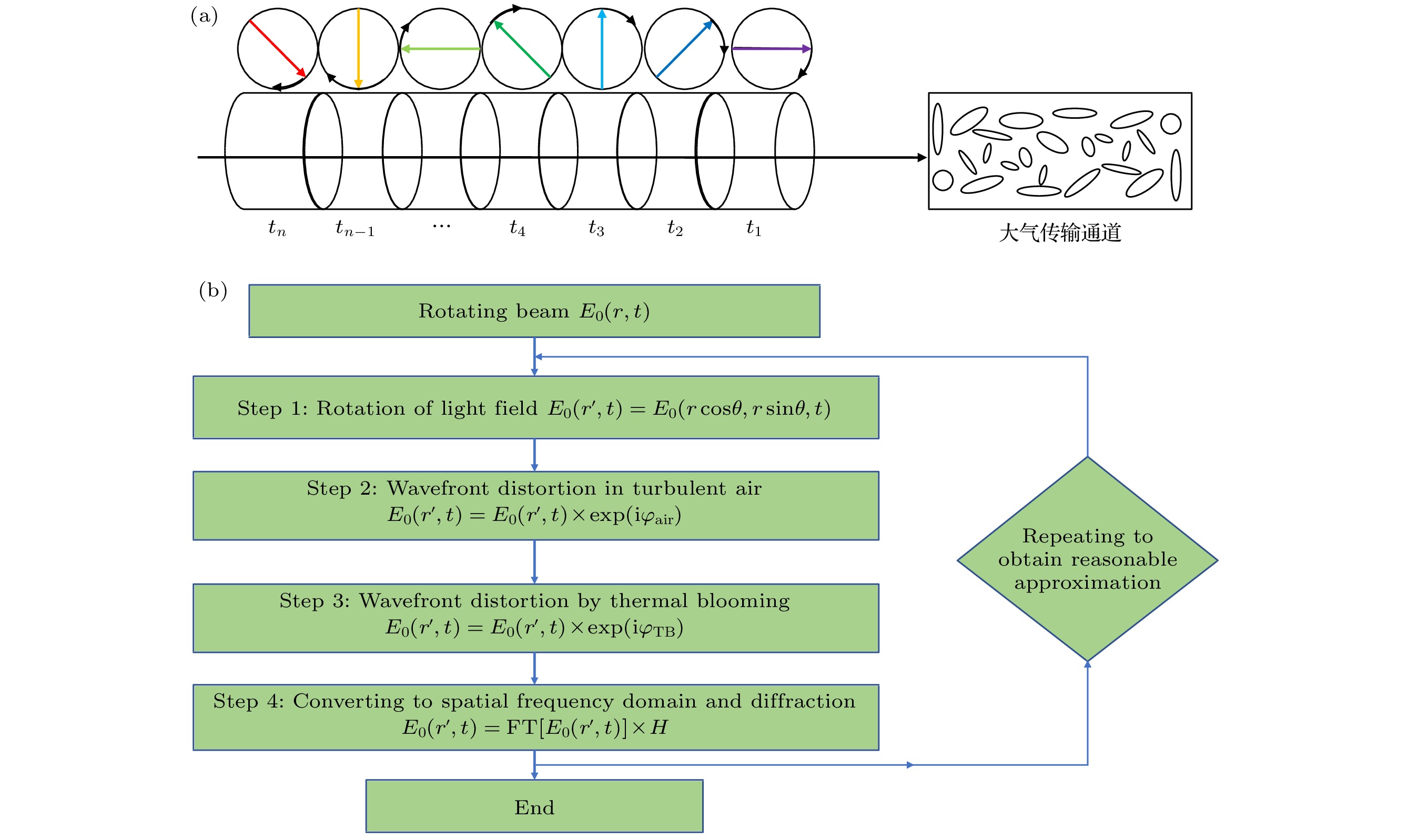
-
The rotating beam is a beam that is generated by the heterodyne interference of vortex beams with different topological charges, whose intensity and wavefront rotate rapidly with time. Under Taylor’s frozen air hypothesis, such a rotating beam, whose rotating period is much shorter than the characteristic time of atmospheric turbulence and the thermal blooming, can travel through all the inhomogeneities due to its rapid rotation during its propagation in the air. The rotation can contribute to the smooth of the wavefront distortion caused by the atmospheric turbulence and the thermal blooming, and thus improve the beam quality and reduce the centroid drift of the rotating beam in far field. The physical model of rotating beam is established by the heterodyne interference of two vortex beams. Taking the atmospheric turbulence and the thermal blooming effect into consideration, the propagation model of the rotating beam in the air is established by using the split-step Fourier method. For simplicity without loss of generality, the influences of the atmospheric turbulence and the thermal blooming effect on the propagation of rotating beam, are both treated as wavefront screen. The difference is that the wavefront screen of atmospheric turbulence is generated by the Kolmogorov power spectrum, while that of thermal blooming is generated by the fluid mechanics equation. The physical mechanism of how the rotating beam mitigates the atmospheric turbulence and the thermal blooming effect is analyzed in detail, that is, when the rotating speed of laser beam is faster than the airflow, the laser beam can pass through all the inhomogeneous and anisotropic atmosphere in the azimuthal direction within the time interval of airflow. After the laser propagates through the frozen air, the total wavefront distortion in the azimuthal direction becomes centrosymmetric with lower PV value, reducing the beam quality degradation. On the basis, the influence of rotation frequency, power ratio of the sub beams, strength of turbulence and thermal blooming on the propagation characteristics of the rotating beam in atmosphere are analyzed. Within a certain range, as the beam rotation frequency increases, the mitigation effect of the rotating beam on atmospheric turbulence and thermal blooming effects are enhanced. With the increase of turbulence intensity and thermal blooming intensity, the mitigation effect of the rotating beam is weakened but still can maintain well, which can provide reference for the engineering applications of laser beam in atmosphere.
[1] Zhang Z, Liang X, Goutsoulas M, Li D, Yang X, Yin S, Xu J, Christodoulides D N, Efremidis N K, Chen Z 2019 APL Photonics 4 076103
Google Scholar
[2] Kwiecień J 2019 Optics Communications 433 200
Google Scholar
[3] 闫玠霖, 韦宏艳, 蔡冬梅, 贾鹏, 乔铁柱 2020 物理学报 69 144203
Google Scholar
Yan J L, Wei H Y, Cai D M, Jia P, Qiao T Z 2020 Acta Phys. Sin. 69 144203
Google Scholar
[4] Zhao L, Wang J, Guo M, Xu X, Qian X, Zhu W, Li J 2021 Opt. Laser Technol. 139 106982
Google Scholar
[5] [6] 张建柱, 张飞舟, 苏华, 胡鹏, 谢晓钢, 罗文 2021 物理学报 70 244202
Google Scholar
Zhang J Z, Zhang F Z, Su H, Hu P, Xie X G, Luo W 2021 Acta Phys. Sin. 70 244202
Google Scholar
[7] Davies R, Kasper M 2012 arXiv: 1201.5741
[8] Booth M J 2014 Light Sci. Appl. 3 e165
Google Scholar
[9] Gu X, Chen L, Krenn M 2020 Opt. Express 28 11033
Google Scholar
[10] Zhong Z, Zhang X, Zhang B, Yuan X 2022 Opt. Express 30 24421
Google Scholar
[11] Qiu D, Tian B, Ting H, Zhong Z, Zhang B 2021 Appl. Opt. 60 8458
Google Scholar
[12] Prasad S 2017 JOSA A 34 931
Google Scholar
[13] Gendron E, Léna P 1996 Astrophys. Space Sci. 239 221
Google Scholar
[14] Schöck M, Spillar E J 2000 JOSA A 17 1650
Google Scholar
[15] Poyneer L, van Dam M, Véran J P 2009 JOSA A 26 833
Google Scholar
[16] Duran V, Djevarhidjian L, de Chatellus H G 2019 Opt. Lett. 44 3789
Google Scholar
[17] Duran V, Schnébelin C, de Chatellus H G 2017 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference (CLEO/Europe-EQEC) Munich, Germany, June 25–29, 2017 p1
[18] Zilberman A, Golbraikh E, Kopeika N S 2008 Appl. Opt. 47 6385
Google Scholar
[19] Vorob'ev V V e 1991 Prog. Quant. Electron. 15 1
Google Scholar
[20] Fleck J A, Morris J, Feit M 1976 Appl. Phys. 10 129
Google Scholar
[21] 吴书云, 李新阳, 罗曦 2018 光电工程 45 170620
Google Scholar
Wu S Y, Li X Y, Luo X 2018 Opto-Electron. Eng. 45 170620
Google Scholar
-
图 1 (a)旋转光束经大气介质传输示意图; (b)旋转光束传输计算流程
Figure 1. (a) Schematic illustration of rotating beam propagating in atmosphere; (b) calculation process of propagation of rotating beam.
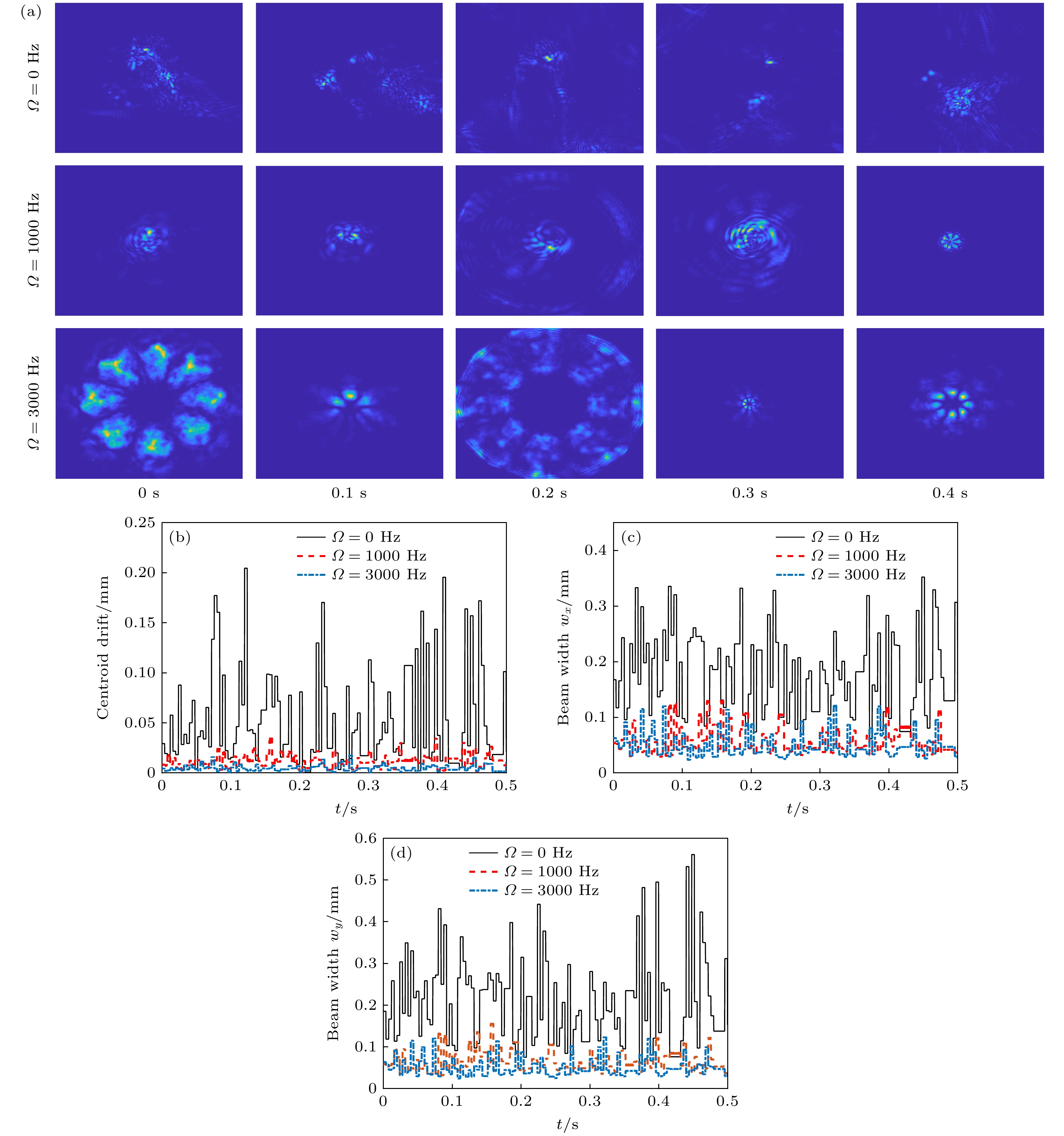
图 2 仅考虑大气湍流(
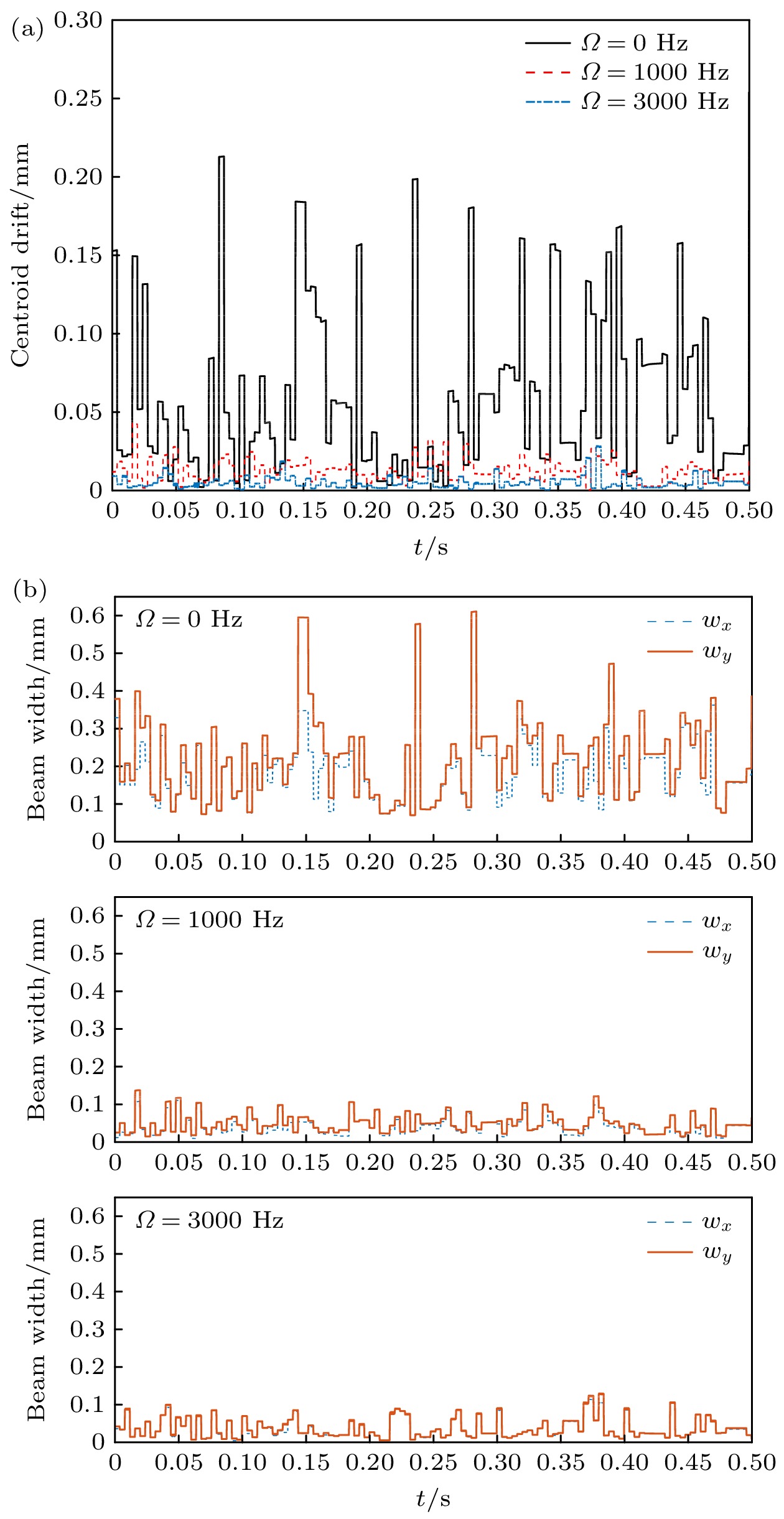
$C_{{n}}^{{2}}$ = 5×10–14 m–2/3)时, 不同旋转频率的旋转光束在大气介质传输特性 (a)旋转光束在不同时刻的近场光强分布; (b)远场质心偏移随时间的变化; (c)远场光斑尺寸wx随时间变化; (d)远场光斑尺寸wy随时间变化Figure 2. Propagation characteristics of rotation beam with different rotation frequency with only atmospheric turbulence considered: (a) Near-field intensity distributions at different time; (b) far-field centroid drift; (c) far-field beam width in x direction; (d) far-field beam width in y direction.
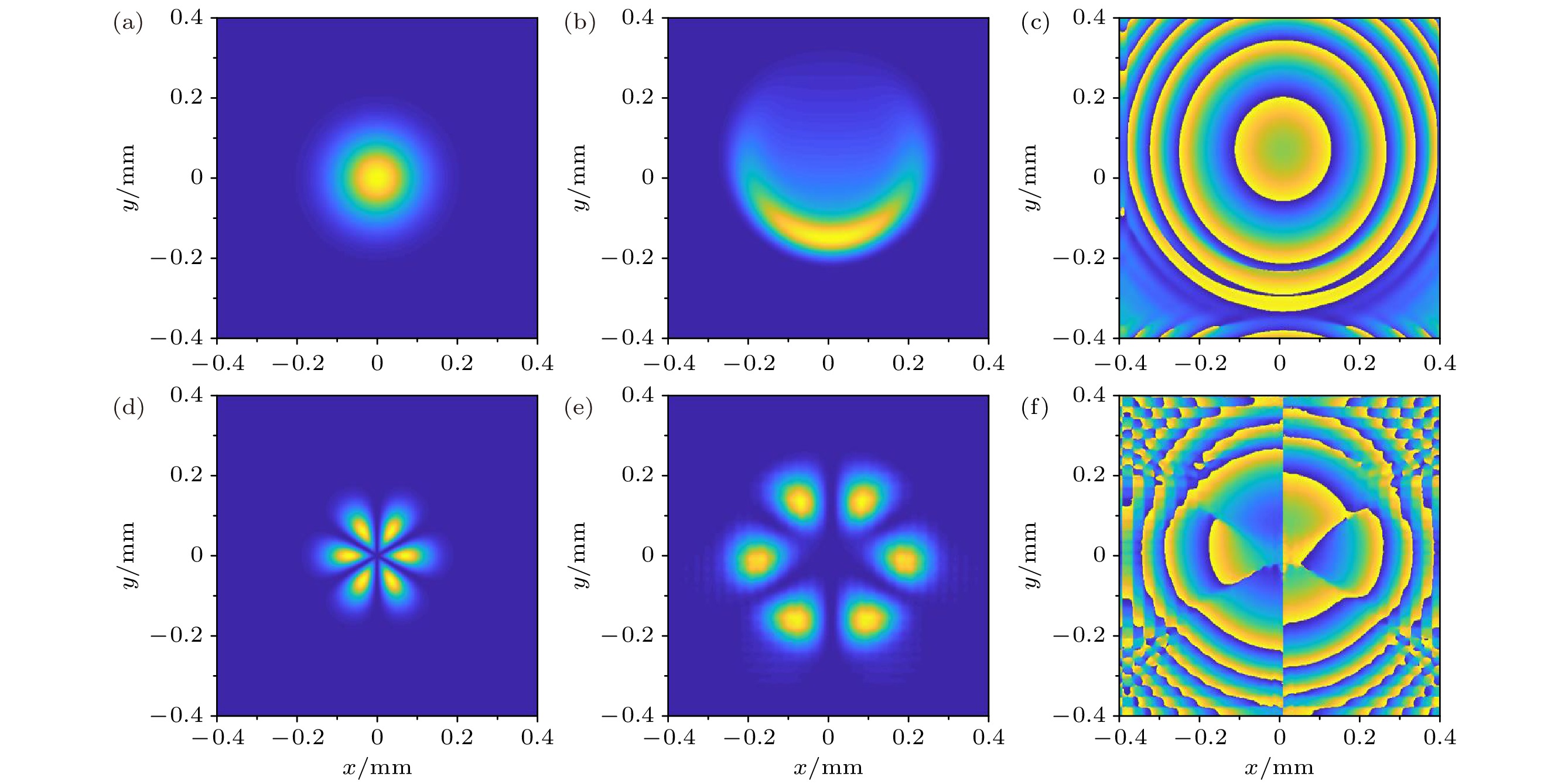
图 3 在仅考虑热晕时, (a)初始高斯光束及其(b)经大气热晕影响后的光强分布, (c)热晕效应引起的大气相位分布; (d)初始花瓣状光束及其(e)经大气热晕影响后的光强分布, (f)热晕效应引起的大气相位分布
Figure 3. Propagation characteristics when only considering thermal blooming effect: (a) Intensity distribution of initial Gaussian beam, (b) intensity distribution of Gaussian beam affected by thermal blooming effect, (c) induced wavefront distribution by thermal blooming; (d) intensity distribution of initial rotating beam with rotation frequency of zero, (e) intensity distribution of rotating beam affected by thermal blooming effect, (f) induced wavefront distribution by thermal blooming.
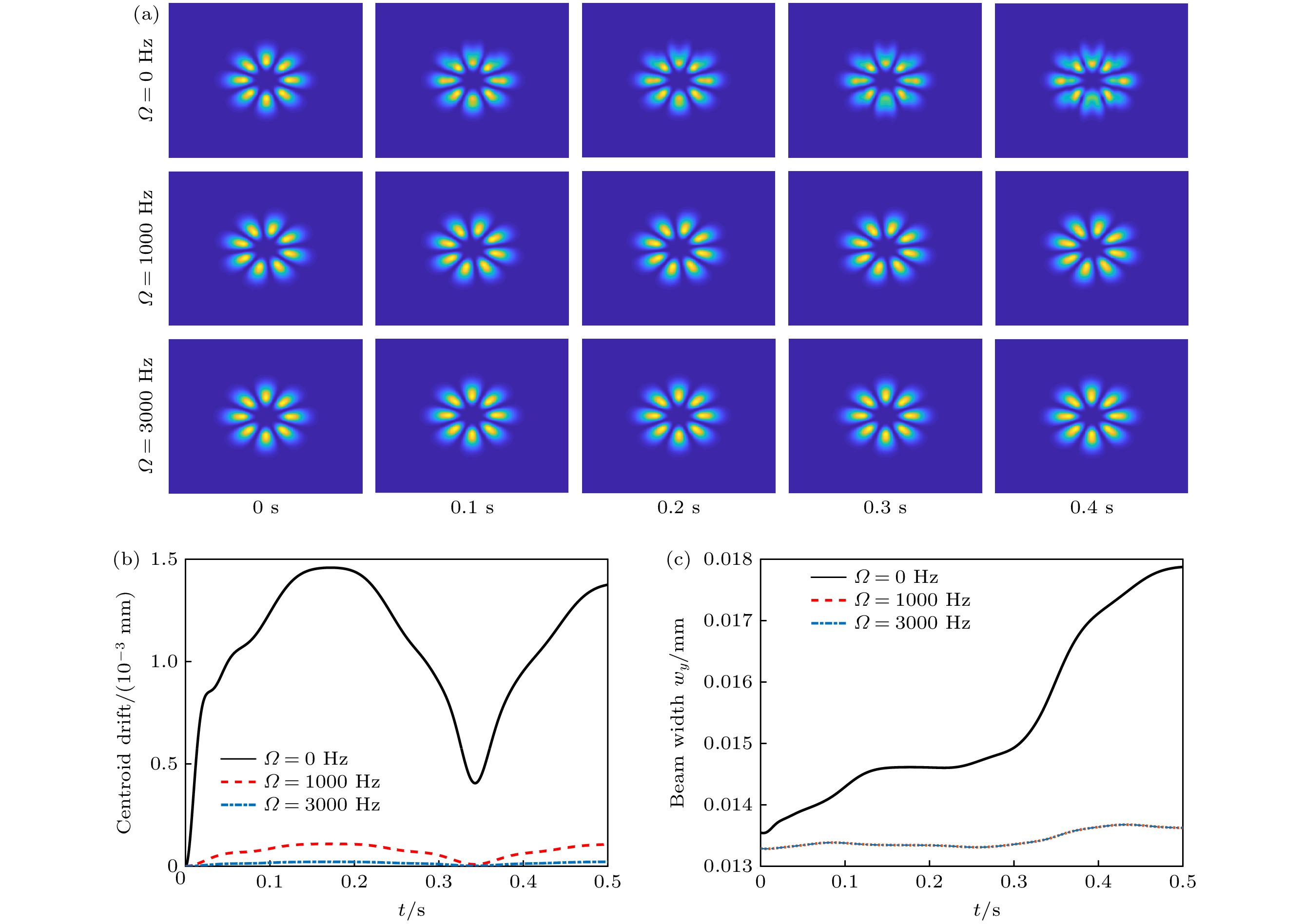
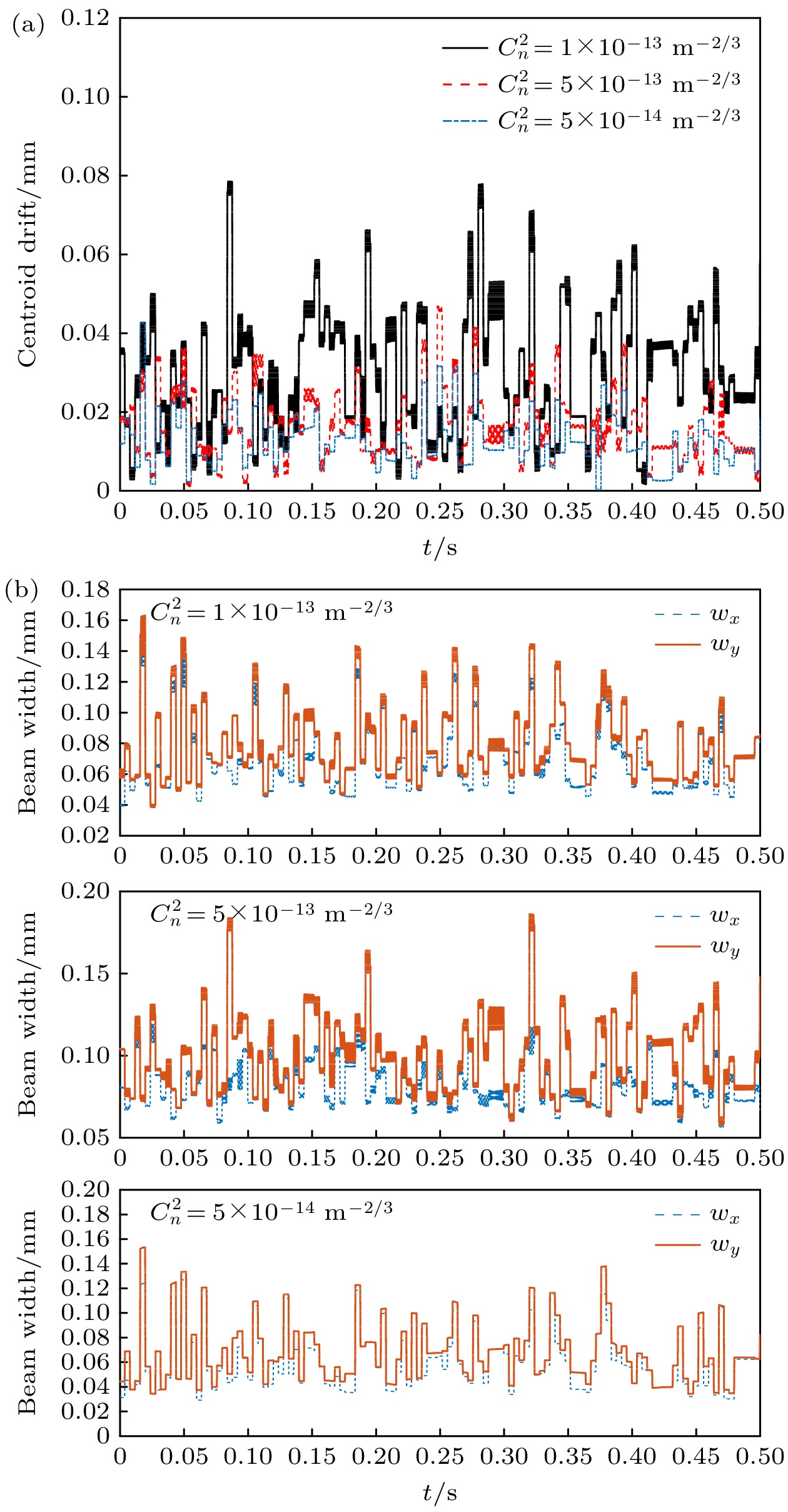
图 4 仅考虑热晕时, 不同频率的旋转光束在大气介质传输特性 (a)旋转光束在不同时刻的近场光强分布; (b)远场质心偏移随时间的变化; (c)远场光斑尺寸wx随时间的变化
Figure 4. Propagation characteristics of rotating beam with different rotation frequency with only thermal blooming considered: (a) Near-field intensity distribution at different seconds; (b) far-field centroid drift; (c) far-field focal-spot size.
图 5 湍流和热晕综合作用下, 旋转光束瞬时光强分布(旋转频率为1000 Hz)
Figure 5. Instantaneous intensity distribution of rotating beam affected by atmospheric turbulence and thermal blooming. The rotation frequency is 1000 Hz.
图 6 不同旋转频率时, 旋转光束大气介质传输特性 (a)远场质心偏移随时间的变化; (b)远场光斑尺寸随时间的变化
Figure 6. Propagation characteristics of rotation beam with different rotation frequency: (a) Far-field centroid drift; (b) far-field beam width.
图 7 远场质心偏移随旋转频率的变化
Figure 7. Variation of far-field centroid drift with rotation frequency.
图 8 不同功率比值时, 旋转光束大气介质传输特性 (a)远场质心偏移随时间的变化; (b)远场光斑尺寸随时间的变化
Figure 8. Propagation characteristics of rotation beam generated by vortex beams with different power ratio: (a) Far-field centroid drift; (b) far-field beam width.
图 9 不同湍流强度时, 旋转光束大气介质传输特性 (a)远场质心偏移随时间的变化; (b)远场光斑尺寸随时间的变化
Figure 9. Propagation characteristics of rotation beam with different turbulence strength: (a) Far-field centroid drift; (b) far-field beam width.
图 10 不同热晕强度时, 旋转光束大气介质传输特性 (a)远场质心偏移随时间的变化; (b)远场光斑尺寸随时间的变化
Figure 10. Propagation characteristics of rotation beam with different beam power: (a) Far-field centroid drift; (b) far-field beam width.
-
[1] Zhang Z, Liang X, Goutsoulas M, Li D, Yang X, Yin S, Xu J, Christodoulides D N, Efremidis N K, Chen Z 2019 APL Photonics 4 076103
Google Scholar
[2] Kwiecień J 2019 Optics Communications 433 200
Google Scholar
[3] 闫玠霖, 韦宏艳, 蔡冬梅, 贾鹏, 乔铁柱 2020 物理学报 69 144203
Google Scholar
Yan J L, Wei H Y, Cai D M, Jia P, Qiao T Z 2020 Acta Phys. Sin. 69 144203
Google Scholar
[4] Zhao L, Wang J, Guo M, Xu X, Qian X, Zhu W, Li J 2021 Opt. Laser Technol. 139 106982
Google Scholar
[5] [6] 张建柱, 张飞舟, 苏华, 胡鹏, 谢晓钢, 罗文 2021 物理学报 70 244202
Google Scholar
Zhang J Z, Zhang F Z, Su H, Hu P, Xie X G, Luo W 2021 Acta Phys. Sin. 70 244202
Google Scholar
[7] Davies R, Kasper M 2012 arXiv: 1201.5741
[8] Booth M J 2014 Light Sci. Appl. 3 e165
Google Scholar
[9] Gu X, Chen L, Krenn M 2020 Opt. Express 28 11033
Google Scholar
[10] Zhong Z, Zhang X, Zhang B, Yuan X 2022 Opt. Express 30 24421
Google Scholar
[11] Qiu D, Tian B, Ting H, Zhong Z, Zhang B 2021 Appl. Opt. 60 8458
Google Scholar
[12] Prasad S 2017 JOSA A 34 931
Google Scholar
[13] Gendron E, Léna P 1996 Astrophys. Space Sci. 239 221
Google Scholar
[14] Schöck M, Spillar E J 2000 JOSA A 17 1650
Google Scholar
[15] Poyneer L, van Dam M, Véran J P 2009 JOSA A 26 833
Google Scholar
[16] Duran V, Djevarhidjian L, de Chatellus H G 2019 Opt. Lett. 44 3789
Google Scholar
[17] Duran V, Schnébelin C, de Chatellus H G 2017 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference (CLEO/Europe-EQEC) Munich, Germany, June 25–29, 2017 p1
[18] Zilberman A, Golbraikh E, Kopeika N S 2008 Appl. Opt. 47 6385
Google Scholar
[19] Vorob'ev V V e 1991 Prog. Quant. Electron. 15 1
Google Scholar
[20] Fleck J A, Morris J, Feit M 1976 Appl. Phys. 10 129
Google Scholar
[21] 吴书云, 李新阳, 罗曦 2018 光电工程 45 170620
Google Scholar
Wu S Y, Li X Y, Luo X 2018 Opto-Electron. Eng. 45 170620
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4339
- PDF Downloads: 91
- Cited By: 0
