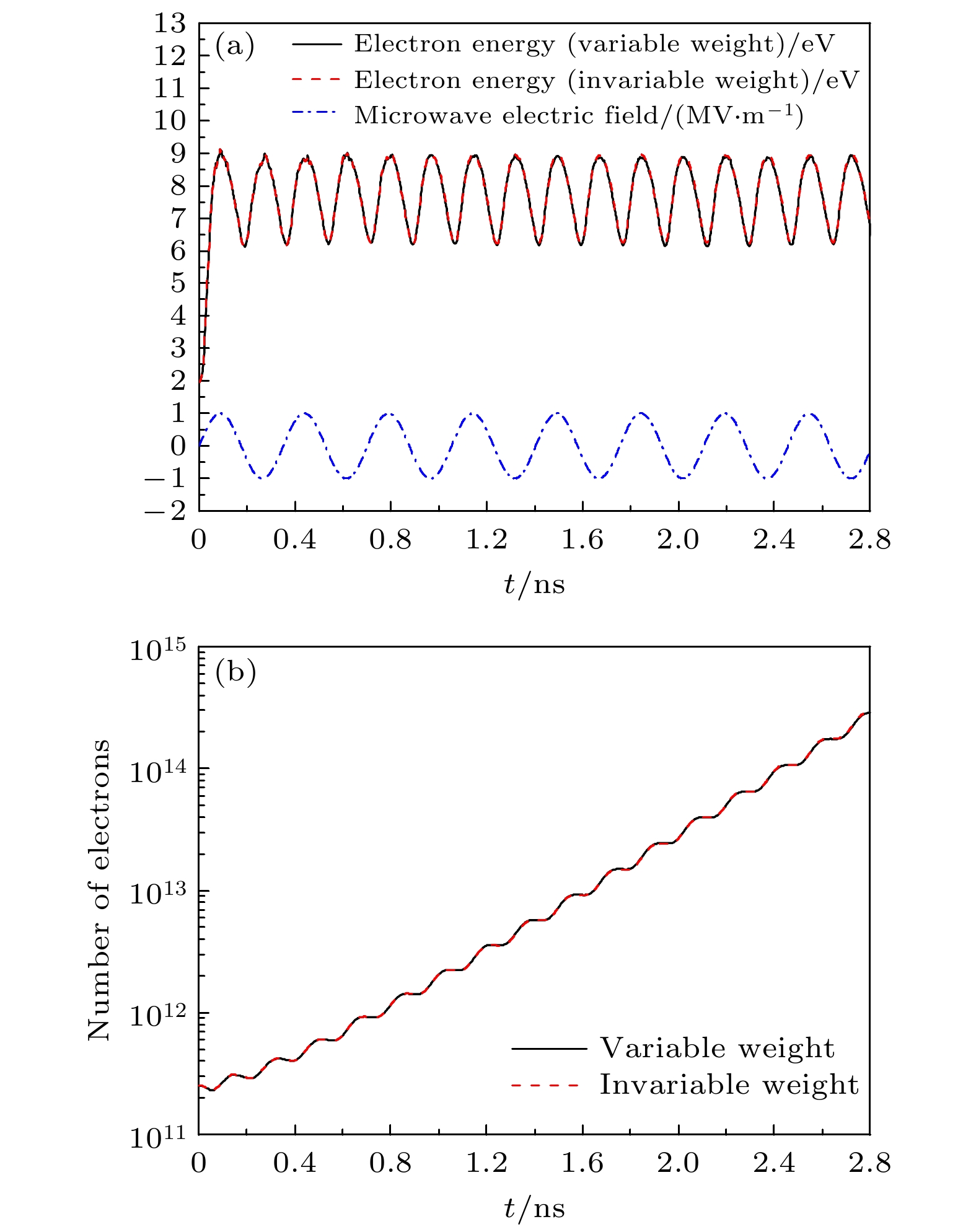
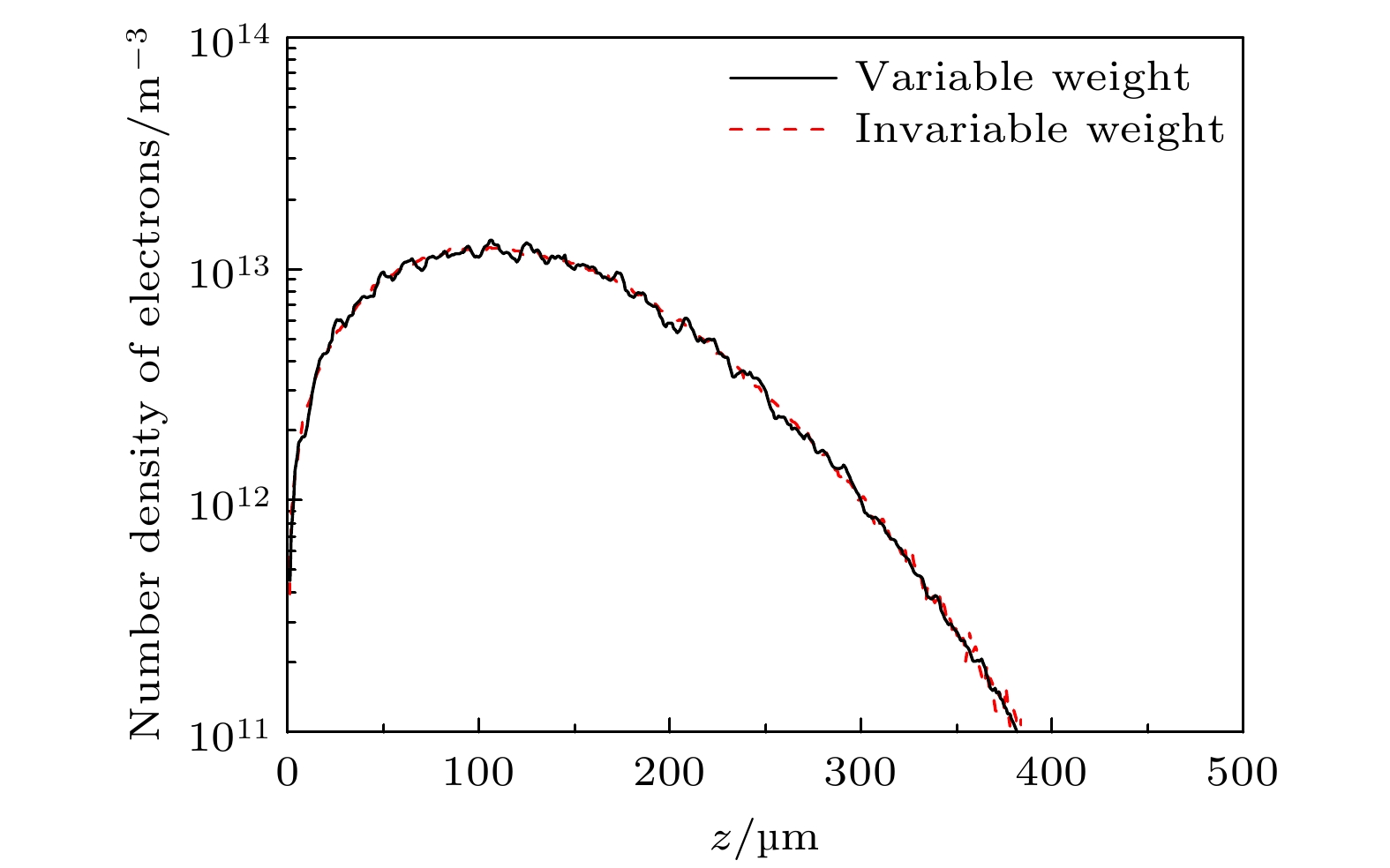
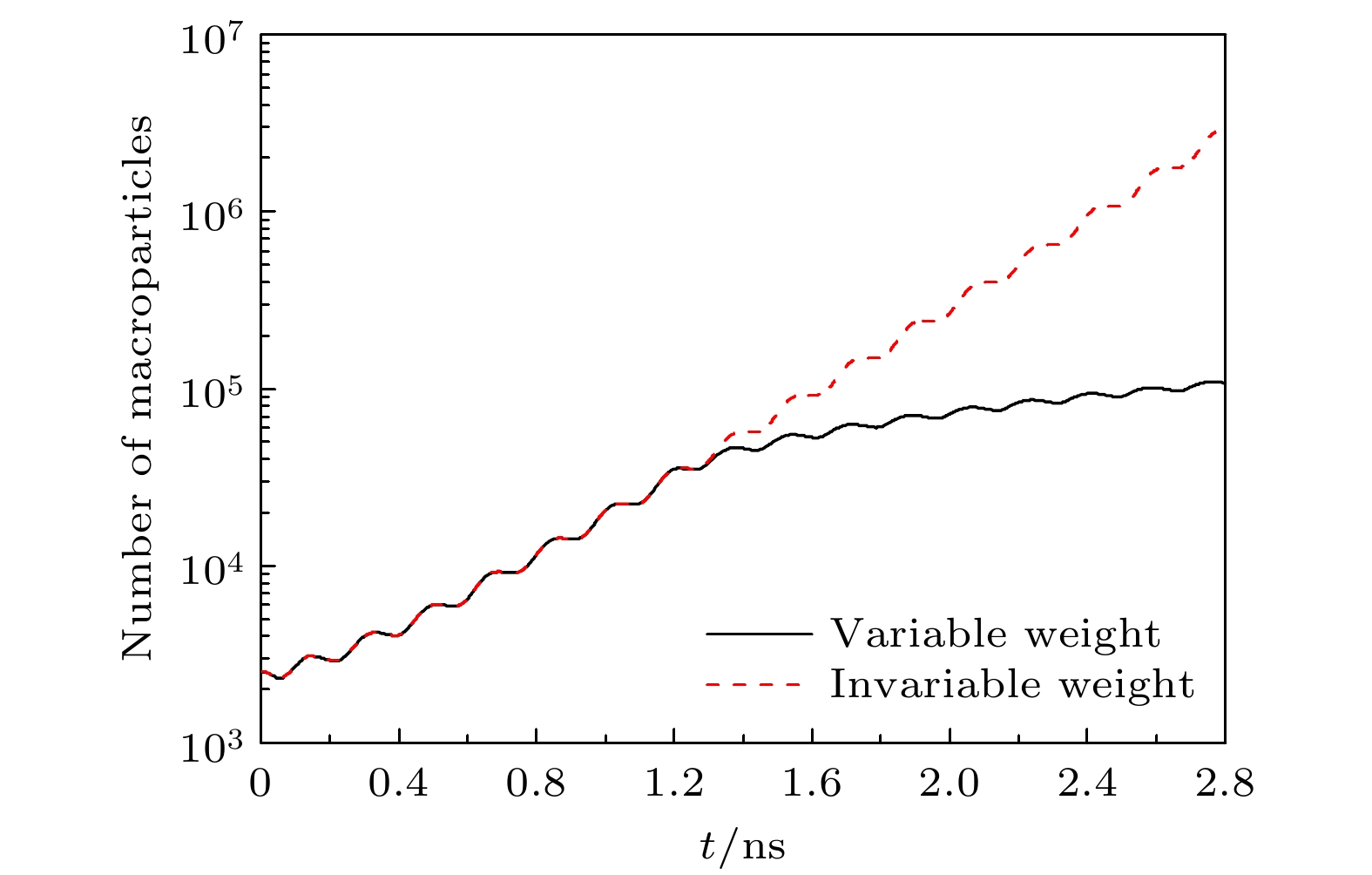
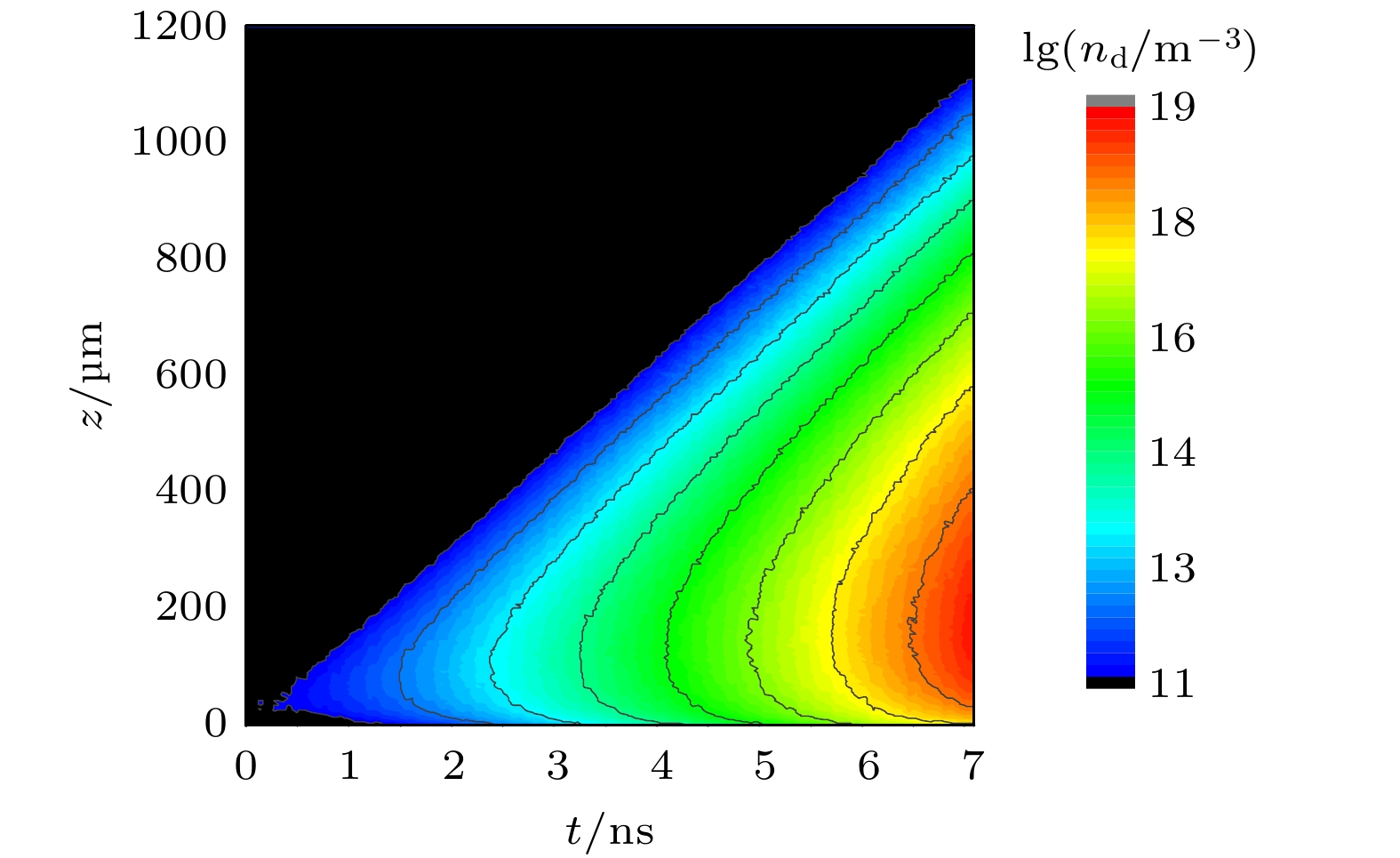
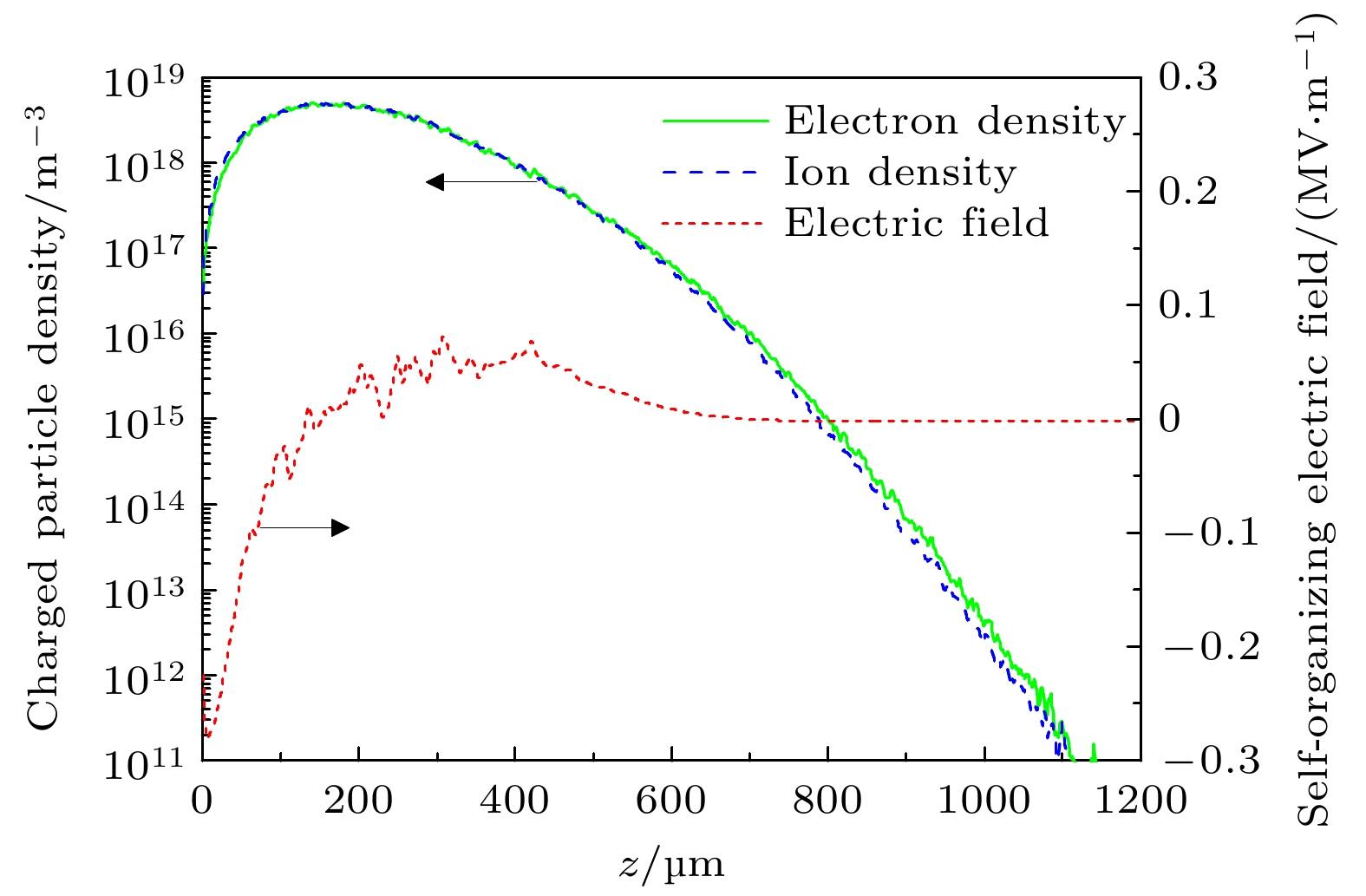
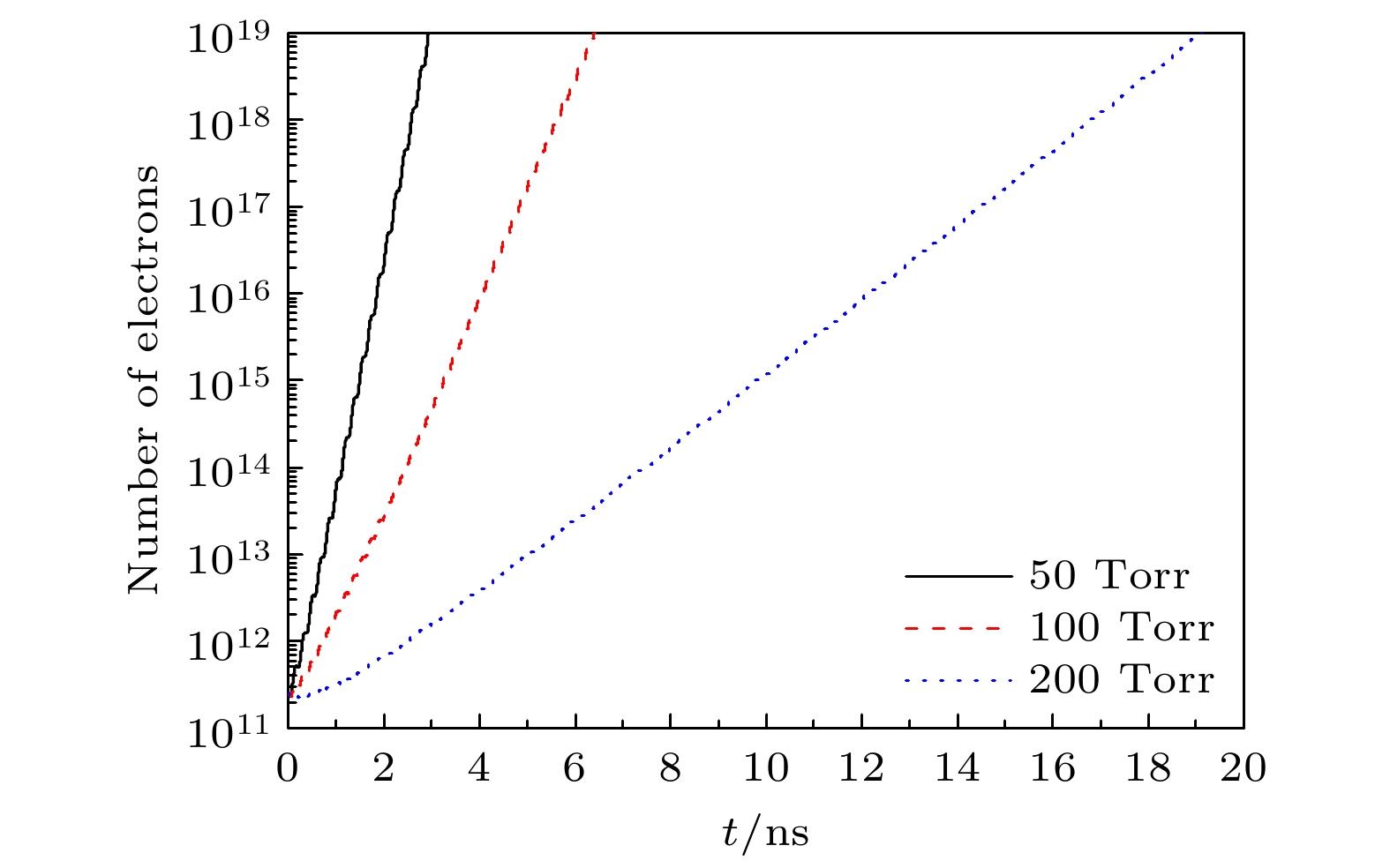
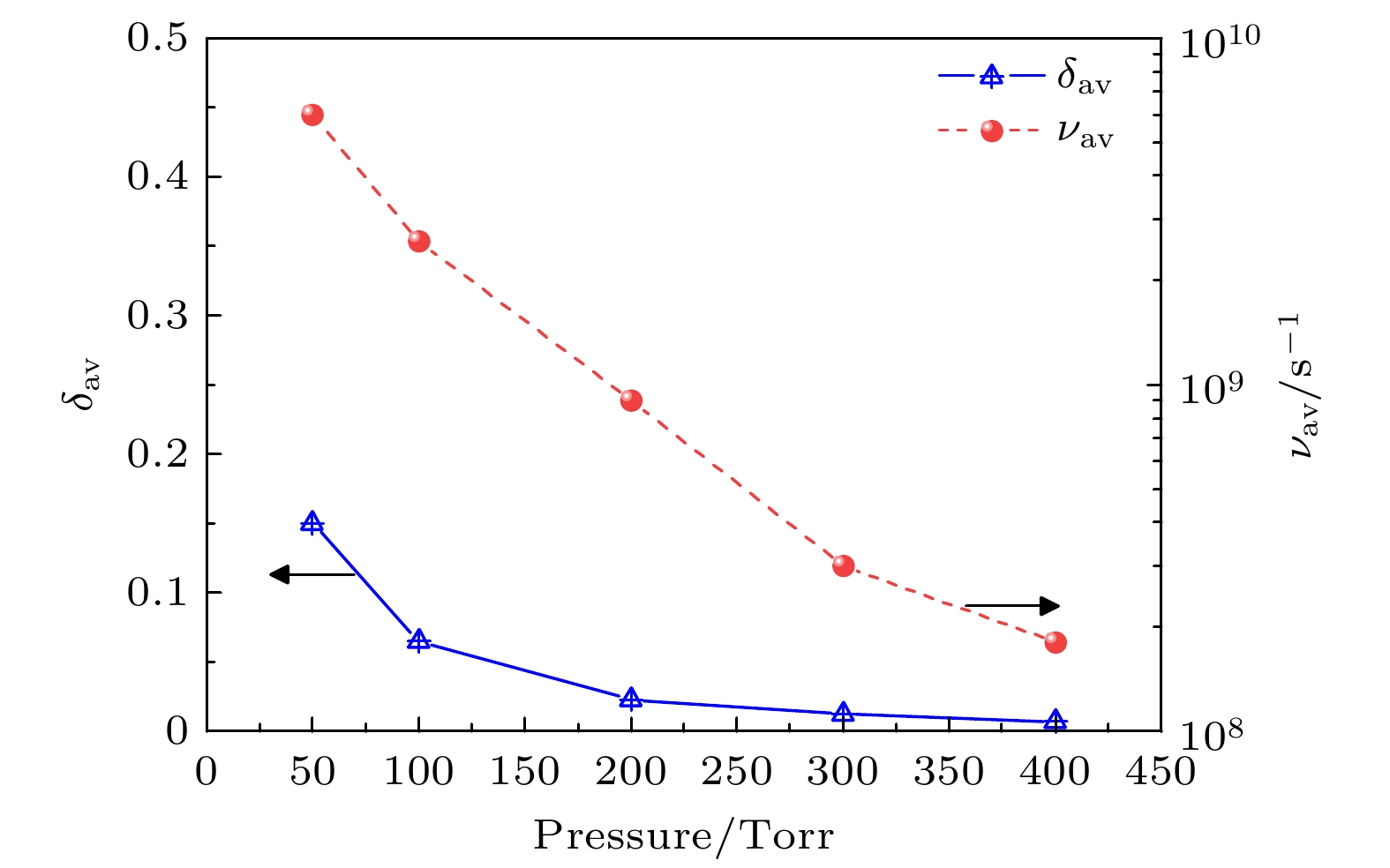
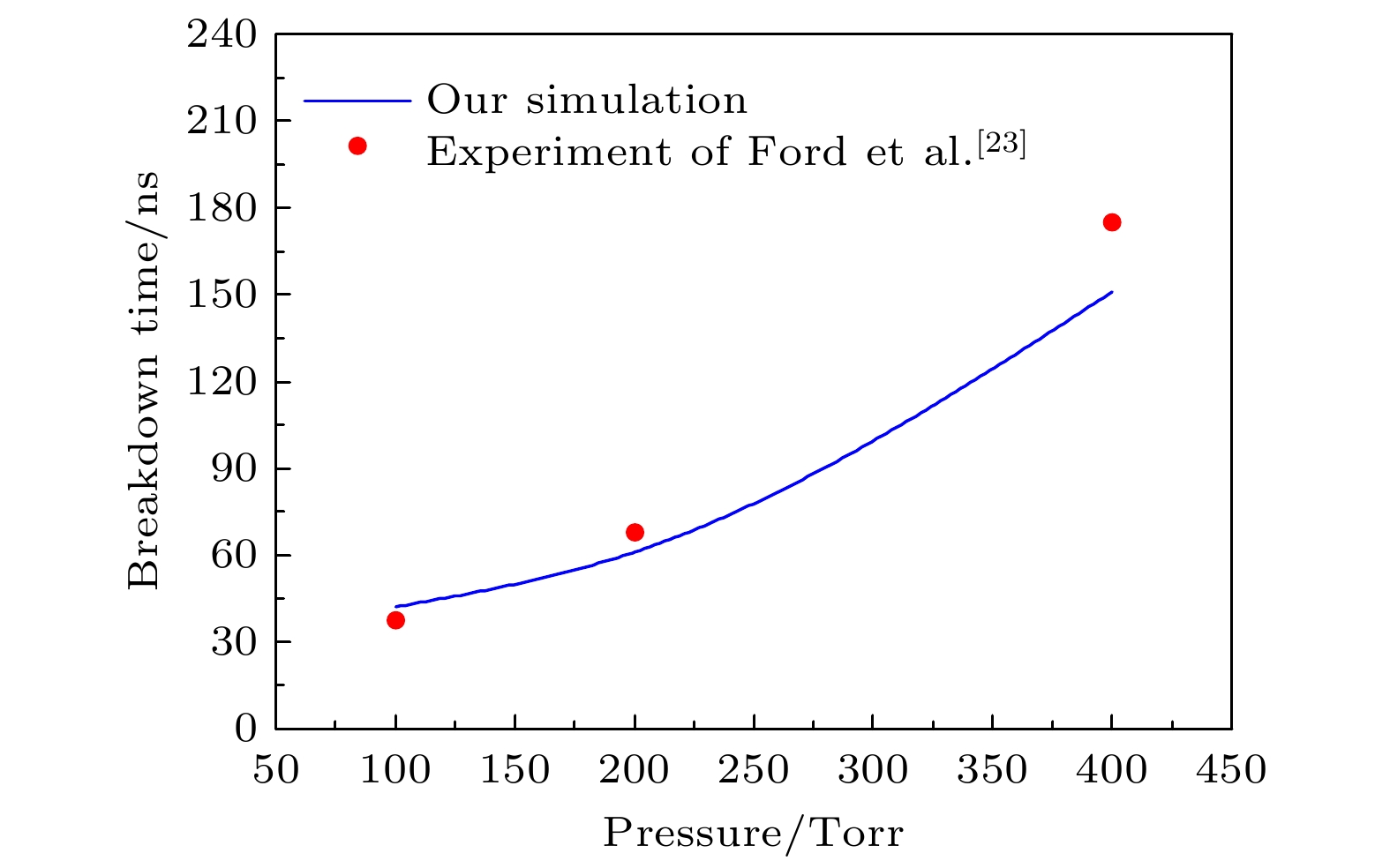
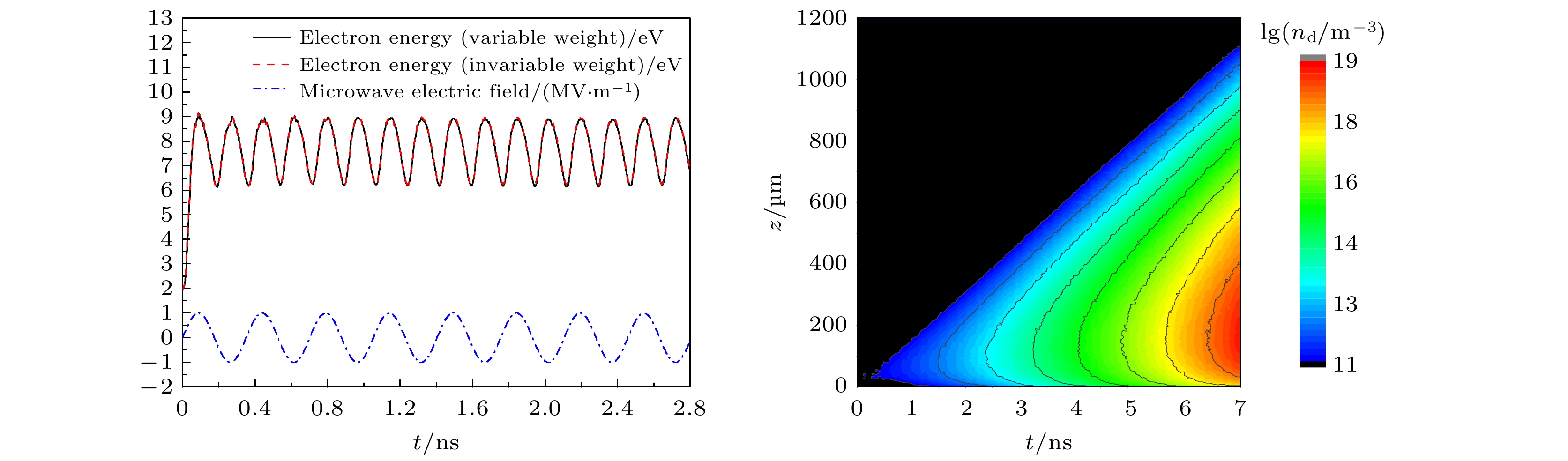
-
Gas breakdown is one of the key factors limiting the increase of power capacity of the outer surface of high-power microwave dielectric window. It is of great significance to conduct corresponding simulation studies. Compared with the fluid model, the particle-in-cell-Monte Carlo collision model has two advantages. One is that the influence of numerical dispersion and instability problems is insignificant, and the other is that it can accurately describe microphysical processes. Therefore, the breakdown characteristics on the gas side of dielectric window are simulated by using the particle-in-cell-Monte Carlo collision model. The two-in-one macro-particle merging method is introduced into the model, thereby greatly reducing the number of macro-particles tracked. Therefore, the whole breakdown process can be simulated and analyzed. The results show that the spatial and temporal evolution of breakdown under the variable macro-particle weight is in good agreement with that under the constant macro-particle weight. This suggests that the two-in-one macro-particle merging method is applicable under the simulation conditions of interest in this paper, i.e., when the ratio of the effective electric field of microwaves to the pressure is between $1.76\times10^3$ and $1.41\times10^4$ V/(m$\cdot$Torr). Since the yield of the secondary electron emission is much less than 1, gas ionization is the dominant mechanism of breakdown on the gas side of dielectric window. Electron ionization and electron diffusion lead the density and thickness of the plasma to significantly increase over time. The peak of electron density does not appear at the dielectric surface, but at a position of 100–150 μm away from the dielectric surface. This is because a large number of electrons are deposited on the dielectric surface, and the accompanying self-organized normal electric field drives the electrons away from the dielectric surface. Because the pressure of background gas of interest in this work is higher than the critical pressure corresponding to the maximum ionization rate (about 10 Torr), the ionization rate decreases monotonically with pressure increasing, resulting in a slower development of breakdown. The accuracy of the particle-in-cell-Monte Carlo collision model is confirmed by comparing the simulated values of breakdown time with experimental data. This work provides an important theoretical basis for understanding and controlling the breakdown on the gas side of dielectric window. The following figure (a) shows that the mean electron energy under the variable macro-particle weight agrees well with that under the constant macro-particle weight at about 100 Torr. The following figure (b) shows that when the plasma density is increased by a factor of 108, the breakdown process can be considered by using the particle-in-cell-Monte Carlo collision model and a two-in-one macro-particle merging method.
-
Keywords:
- gas breakdown /
- dielectric surface /
- high-power microwave /
- particle-in-cell-Monte Carlo collision model /
- macro-particle merging method
[1] Schaub S C, Shapiro M A, Temkin R J 2019 Phys. Rev. Lett. 123 175001
Google Scholar
[2] 杨浩, 黄诺慈, 刘星辰, 郑强林, 鲍向阳, 闫二艳 2024 强激光与粒子束 36 043031
Google Scholar
Yang H, Huang N C, Liu X C, Zheng Q L, Bao X Y, Yan E Y 2024 High Power Laser and Particle Beams 36 043031
Google Scholar
[3] Wen D Q, Zhang P, Krek J, Fu Y, Verboncoeur J P 2022 Phys. Rev. Lett. 129 045001
Google Scholar
[4] Chang C, Fang J Y, Zhang Z Q, Chen C, Tang C, Jin Q 2010 Appl. Phys. Lett. 97 141501
Google Scholar
[5] Zhao P, Wang R, Guo L 2022 Plasma Sources Sci. Technol. 31 095005
Google Scholar
[6] Wang H, Liu L, Liu D, Meng L 2022 IEEE Trans. Electron Dev. 69 4598
Google Scholar
[7] Kim H C, Verboncoeur J P 2006 Phys. Plasmas 13 123506
Google Scholar
[8] 蔡利兵, 王建国 2010 物理学报 59 1143
Google Scholar
Cai L B, Wang J G 2010 Acta Phys. Sin. 59 1143
Google Scholar
[9] 董烨, 董志伟, 周前红, 杨温渊, 周海京 2014 物理学报 63 067901
Google Scholar
Dong Y, Dong Z W, Zhou Q H, Yang W Y, Zhou H J 2014 Acta Phys. Sin. 63 067901
Google Scholar
[10] 常超 2018 科学通报 63 1391
Chang C 2018 Chin Sci. Bull. 63 1391
[11] 左春彦, 高飞, 戴忠玲, 王友年 2018 物理学报 67 225201
Google Scholar
Zuo C Y, Gao F, Dai Z L, Wang Y N 2018 Acta Phys. Sin. 67 225201
Google Scholar
[12] 舒盼盼, 赵朋程, 王瑞 2023 物理学报 72 095202
Google Scholar
Shu P P, Zhao P C, Wang R 2023 Acta Phys. Sin. 72 095202
Google Scholar
[13] Iqbal A, Wen D Q, Verboncoeur J, Zhang P 2023 High Voltage 8 1095
Google Scholar
[14] Zhao P, Liu Z, Wang R, Shu P, Guo L, Cao X 2024 Plasma Sci. Technol. 26 045401
Google Scholar
[15] 孟祥琛, 王丹, 蔡亚辉, 叶振, 贺永宁, 徐亚男 2023 物理学报 72 107901
Google Scholar
Meng X C, Wang D, Cai Y H, Ye Z, He Y N, Xu Y N 2023 Acta Phys. Sin. 72 107901
Google Scholar
[16] Hu T, Zhu S, Zhao Y, Sun X, Yang J, He Y, Wang X, Bai C, Bai H, Wei H, Cao M, Hu Z, Liu M, Cui W 2022 Chin. Phys. B 31 047901
Google Scholar
[17] Chang C, Liu G, Tang C, Chen C, Fang J 2011 Phys. Plasmas 18 055702
Google Scholar
[18] Chang C, Liu Y S, Verboncoeur J, Chen C H, Guo L T, Li S, Wu X L 2015 Appl. Phys. Lett. 106 014102
Google Scholar
[19] Langellotti S V, Brusstar A, Jordan N M, Lau Y Y, Gilgenbach R M 2023 IEEE Trans. Electron Dev. 70 5871
Google Scholar
[20] Zuo C Y, Gao F, Dai Z L, Wang Y N 2023 Phys. Plasmas 30 062101
Google Scholar
[21] Wen D Q, Iqbal A, Zhang P, Verboncoeur J P 2022 Appl. Phys. Lett. 121 164103
Google Scholar
[22] Zhang J, Jiang M, Luo W, Wang H, Li Y, Liu C 2020 J. Appl. Phys. 128 143301
Google Scholar
[23] Ford P J, Beeson S R, Krompholz H G, Neuber A A 2012 Phys. Plasmas 19 073503
Google Scholar
[24] 周前红, 董烨, 董志伟, 周海京 2015 物理学报 64 085201
Google Scholar
Zhou Q H, Dong Y, Dong Z W, Zhou H J 2015 Acta Phys. Sin. 64 085201
Google Scholar
[25] Teunissen J, Ebert U 2014 J. Comput. Phys. 259 318
Google Scholar
[26] Peterson L R, Allen J E 1972 J. Chem. Phys. 56 6068
Google Scholar
[27] Vaughan J R M 1989 IEEE Trans. Electron Devices 36 1963
Google Scholar
[28] Lau Y Y, Verboncoeur J P, Kim H C 2006 Appl. Phys. Lett. 89 261501
Google Scholar
-
图 1 高功率微波作用下介质窗气体侧击穿的示意图
Figure 1. Schematic diagram of breakdown on gas side of dielectric window of high power microwave.
图 2 在背景气体压强为100 Torr和宏粒子权重分别为变量与常数下, (a)平均电子能量, 微波电场以及(b)电子数量随时间的变化
Figure 2. The change of (a) mean electron energy, microwave electric field, and (b) number of electrons over time with the macro-particle weights as variables and constant, respectively. The background gas pressure is 100 Torr in this figure.
图 3 在背景气体压强为100 Torr和宏粒子权重分别为变量与常数下, $ t=2.5\; {\mathrm{ns}}$时的电子数密度随坐标z的变化
Figure 3. The variation of electron number density with coordinate z at time $ t=2.5\; {\mathrm{ns}}$ when the weights of macro–particles are variables and a constant, respectively. The background gas pressure is 100 Torr in this figure.
图 4 在背景气体压强为100 Torr和宏粒子权重分别为变量与常数时, 代表电子的宏粒子数量随时间的变化
Figure 4. The variation of the number of macro–particles representing electrons over time when the weights of macro–particles are variables and a constant, respectively. The background gas pressure is 100 Torr in this figure.
图 5 背景气体压强为100 Torr下电子密度$ n_\mathrm{d} $随时间和空间的变化
Figure 5. The variation of electron density $ n_\mathrm{d} $ with time and space under background gas pressure of 100 Torr.
图 6 背景气体压强为100 Torr下带电粒子密度和自组织法向电场$ E_\mathrm{n} $在$ t=7 $ ns时的空间分布
Figure 6. Spatial profiles of charged particle density and self-organizing normal electric field $ E_\mathrm{n} $ at time $ t=7 $ ns under background gas pressure of 100 Torr.
图 7 背景气体压强分别为50, 100和200 Torr时电子数量随时间的变化
Figure 7. Change in the number of electrons over time under background gas pressures of 50, 100 and 200 Torr.
图 8 电离率与 次级电子发射产额关于时间的平均值$ \nu_{\mathrm{av}} $和$ \delta_{\mathrm{av}} $随背景气体压强的变化
Figure 8. The average values $ \nu_{\mathrm{av}} $ and $ \delta_{\mathrm{av}} $ of ionization rate and secondary electron emission yield with respect to time as a function of background gas pressure.
-
[1] Schaub S C, Shapiro M A, Temkin R J 2019 Phys. Rev. Lett. 123 175001
Google Scholar
[2] 杨浩, 黄诺慈, 刘星辰, 郑强林, 鲍向阳, 闫二艳 2024 强激光与粒子束 36 043031
Google Scholar
Yang H, Huang N C, Liu X C, Zheng Q L, Bao X Y, Yan E Y 2024 High Power Laser and Particle Beams 36 043031
Google Scholar
[3] Wen D Q, Zhang P, Krek J, Fu Y, Verboncoeur J P 2022 Phys. Rev. Lett. 129 045001
Google Scholar
[4] Chang C, Fang J Y, Zhang Z Q, Chen C, Tang C, Jin Q 2010 Appl. Phys. Lett. 97 141501
Google Scholar
[5] Zhao P, Wang R, Guo L 2022 Plasma Sources Sci. Technol. 31 095005
Google Scholar
[6] Wang H, Liu L, Liu D, Meng L 2022 IEEE Trans. Electron Dev. 69 4598
Google Scholar
[7] Kim H C, Verboncoeur J P 2006 Phys. Plasmas 13 123506
Google Scholar
[8] 蔡利兵, 王建国 2010 物理学报 59 1143
Google Scholar
Cai L B, Wang J G 2010 Acta Phys. Sin. 59 1143
Google Scholar
[9] 董烨, 董志伟, 周前红, 杨温渊, 周海京 2014 物理学报 63 067901
Google Scholar
Dong Y, Dong Z W, Zhou Q H, Yang W Y, Zhou H J 2014 Acta Phys. Sin. 63 067901
Google Scholar
[10] 常超 2018 科学通报 63 1391
Chang C 2018 Chin Sci. Bull. 63 1391
[11] 左春彦, 高飞, 戴忠玲, 王友年 2018 物理学报 67 225201
Google Scholar
Zuo C Y, Gao F, Dai Z L, Wang Y N 2018 Acta Phys. Sin. 67 225201
Google Scholar
[12] 舒盼盼, 赵朋程, 王瑞 2023 物理学报 72 095202
Google Scholar
Shu P P, Zhao P C, Wang R 2023 Acta Phys. Sin. 72 095202
Google Scholar
[13] Iqbal A, Wen D Q, Verboncoeur J, Zhang P 2023 High Voltage 8 1095
Google Scholar
[14] Zhao P, Liu Z, Wang R, Shu P, Guo L, Cao X 2024 Plasma Sci. Technol. 26 045401
Google Scholar
[15] 孟祥琛, 王丹, 蔡亚辉, 叶振, 贺永宁, 徐亚男 2023 物理学报 72 107901
Google Scholar
Meng X C, Wang D, Cai Y H, Ye Z, He Y N, Xu Y N 2023 Acta Phys. Sin. 72 107901
Google Scholar
[16] Hu T, Zhu S, Zhao Y, Sun X, Yang J, He Y, Wang X, Bai C, Bai H, Wei H, Cao M, Hu Z, Liu M, Cui W 2022 Chin. Phys. B 31 047901
Google Scholar
[17] Chang C, Liu G, Tang C, Chen C, Fang J 2011 Phys. Plasmas 18 055702
Google Scholar
[18] Chang C, Liu Y S, Verboncoeur J, Chen C H, Guo L T, Li S, Wu X L 2015 Appl. Phys. Lett. 106 014102
Google Scholar
[19] Langellotti S V, Brusstar A, Jordan N M, Lau Y Y, Gilgenbach R M 2023 IEEE Trans. Electron Dev. 70 5871
Google Scholar
[20] Zuo C Y, Gao F, Dai Z L, Wang Y N 2023 Phys. Plasmas 30 062101
Google Scholar
[21] Wen D Q, Iqbal A, Zhang P, Verboncoeur J P 2022 Appl. Phys. Lett. 121 164103
Google Scholar
[22] Zhang J, Jiang M, Luo W, Wang H, Li Y, Liu C 2020 J. Appl. Phys. 128 143301
Google Scholar
[23] Ford P J, Beeson S R, Krompholz H G, Neuber A A 2012 Phys. Plasmas 19 073503
Google Scholar
[24] 周前红, 董烨, 董志伟, 周海京 2015 物理学报 64 085201
Google Scholar
Zhou Q H, Dong Y, Dong Z W, Zhou H J 2015 Acta Phys. Sin. 64 085201
Google Scholar
[25] Teunissen J, Ebert U 2014 J. Comput. Phys. 259 318
Google Scholar
[26] Peterson L R, Allen J E 1972 J. Chem. Phys. 56 6068
Google Scholar
[27] Vaughan J R M 1989 IEEE Trans. Electron Devices 36 1963
Google Scholar
[28] Lau Y Y, Verboncoeur J P, Kim H C 2006 Appl. Phys. Lett. 89 261501
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 514
- PDF Downloads: 22
- Cited By: 0
