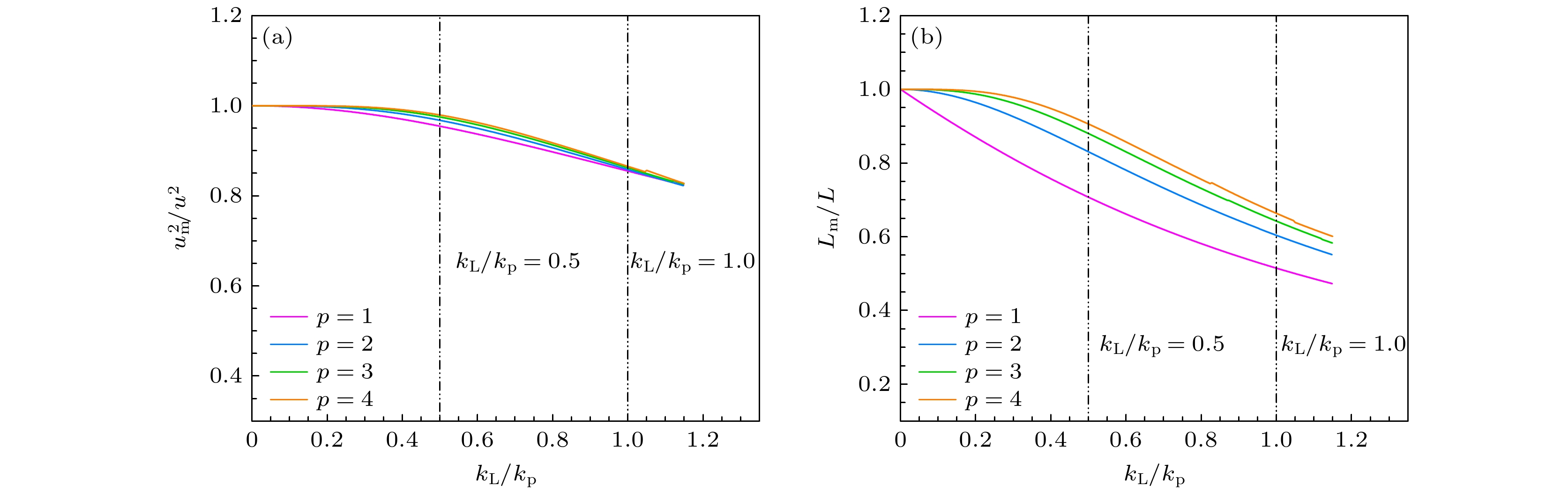
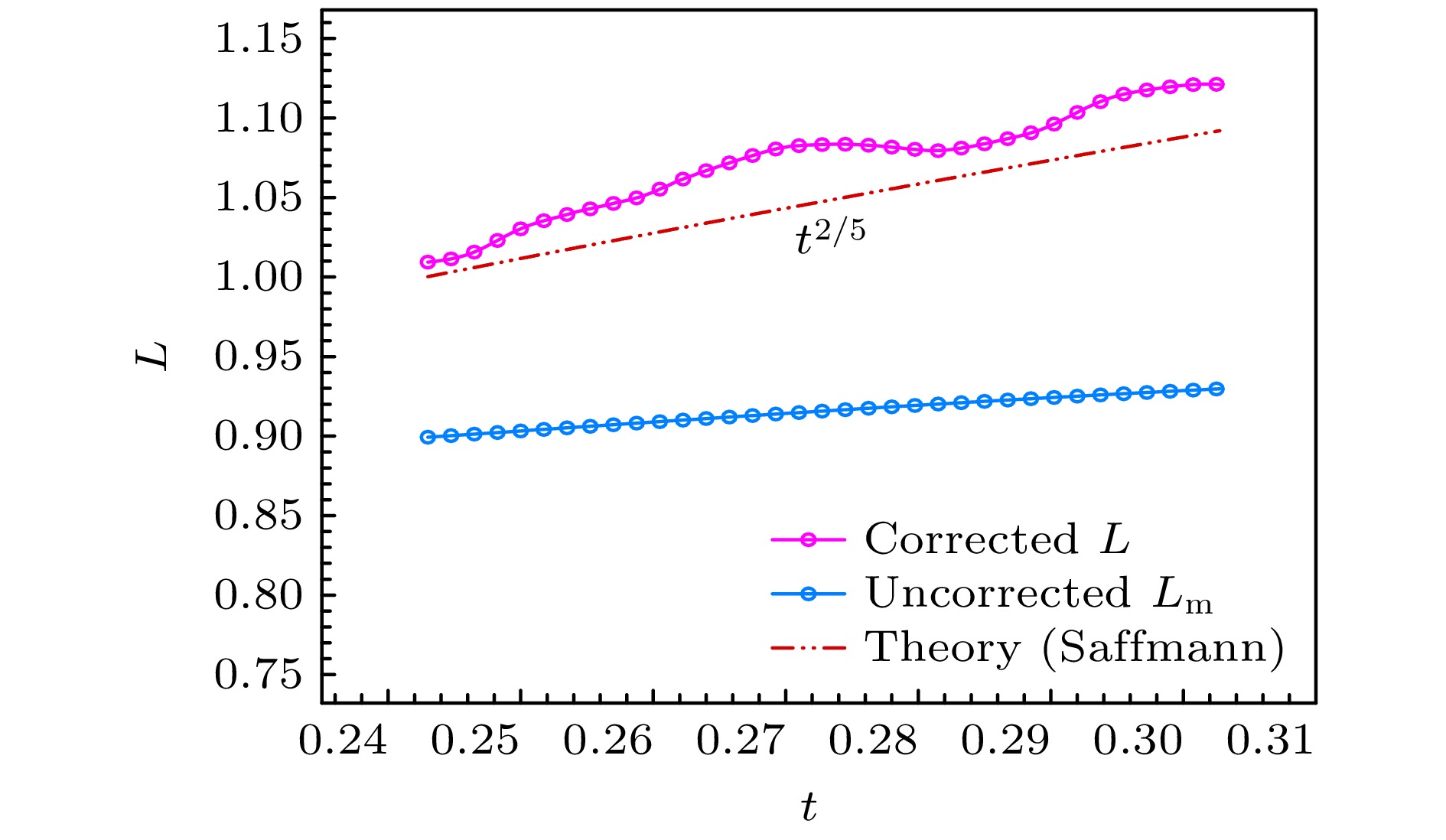
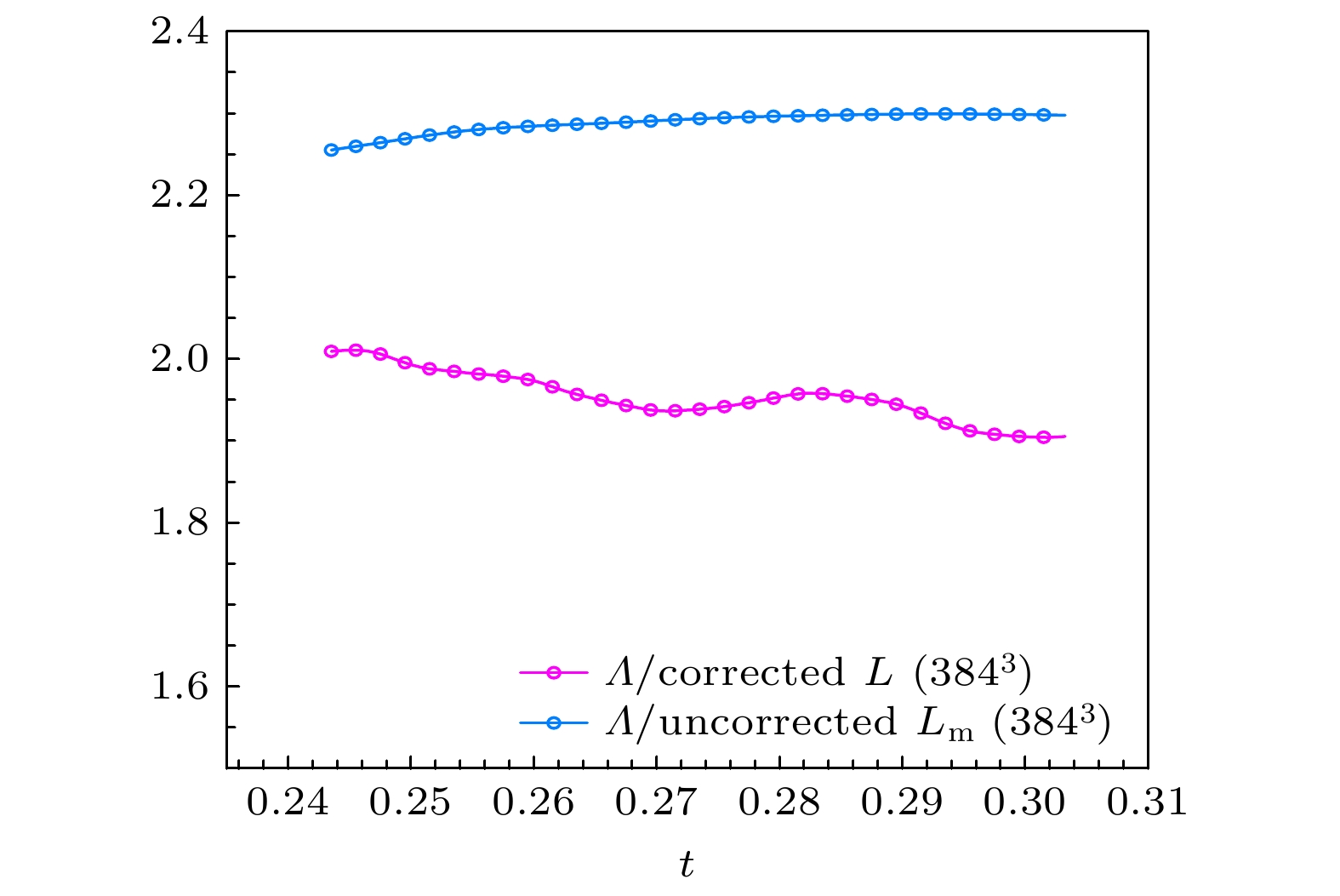
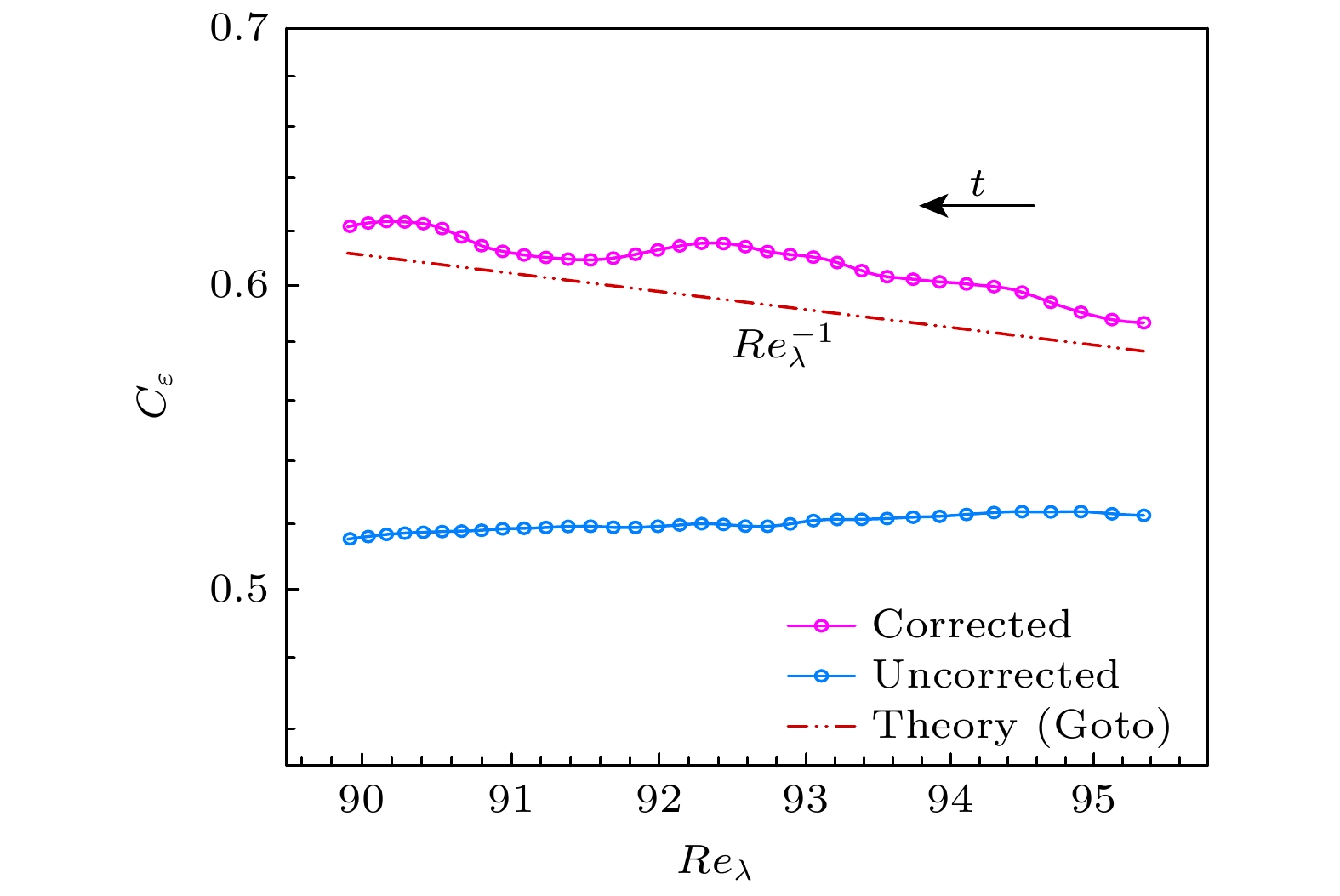
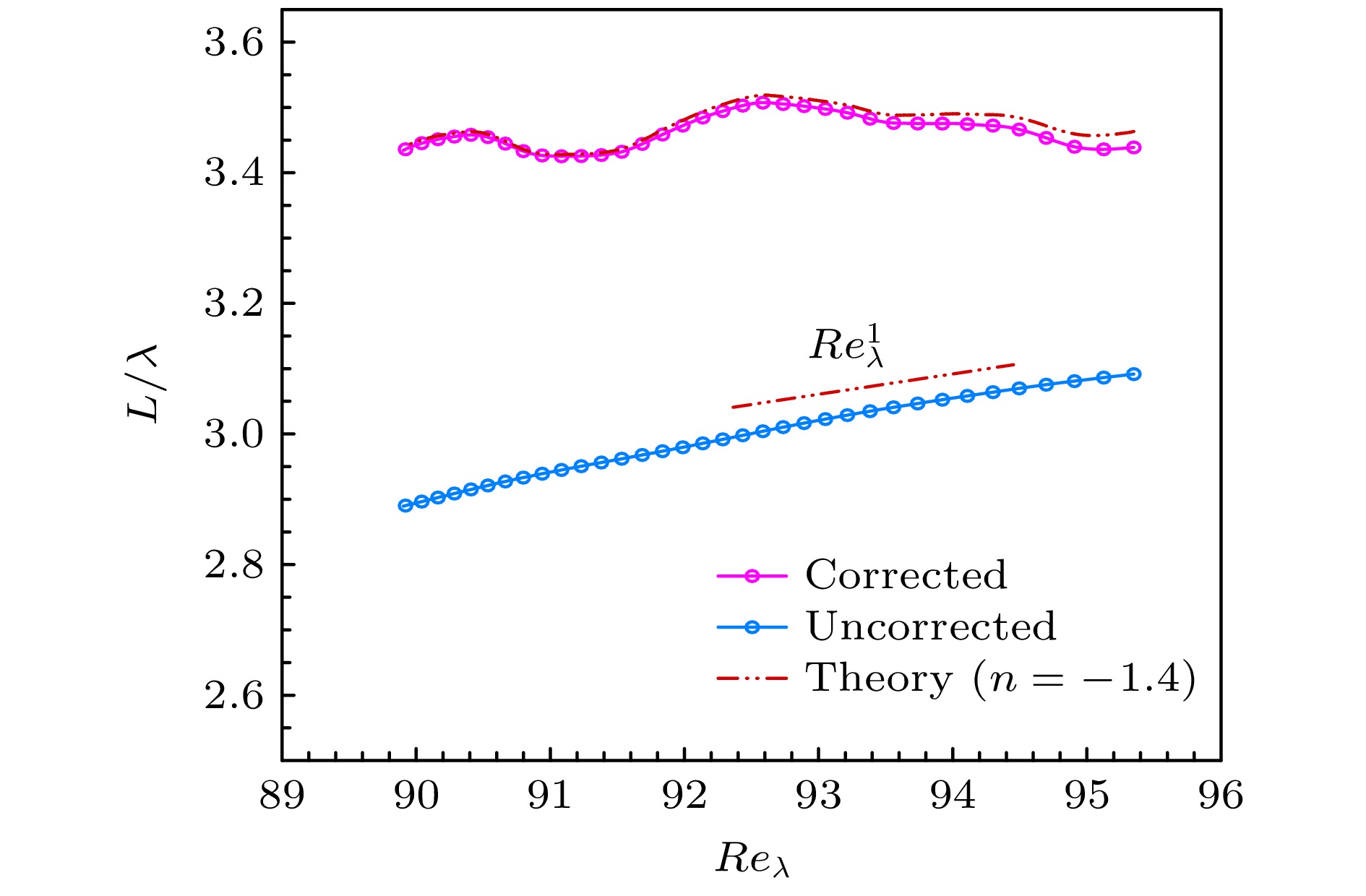
-
Turbulence modeling relies critically on accurate characterization of large-scale structures, with the integral length scale $ L $ serving as a key parameter for industrial applications ranging from combustion stability optimization to wind farm design and aerodynamic load prediction. However, direct numerical simulation (DNS) of turbulence faces inherent limitations in resolving all wavenumbers within the low-wavenumber region of the turbulent kinetic energy spectrum due to finite computational domain sizes. This unresolved low-wavenumber deficiency leads to incomplete characterization of large-scale structures and introduces systematic deviations in key statistical quantities, particularly the integral length scale $ L $ and turbulence dissipation coefficient $ {C}_{\varepsilon } $. As turbulence evolves, the spectral peak wavenumber $ {k}_{p} $ migrates toward lower wavenumbers, exacerbating the loss of large-scale information and causing computed statistics to diverge from physical reality. In this study, we perform high-fidelity DNS of homogeneous isotropic decaying turbulence in a periodic cubic domain of side length 4π with $ {384}^{3} $ grid points. The DNS is executed by using a standard pseudospectral solver and a fourth-order Runge-Kutta time integration scheme, with a semi-implicit treatment of the viscous term. The spatial resolution $ {k}_{\mathrm{m}\mathrm{a}\mathrm{x}}\eta =1.65 $ ensures adequate resolution of dissipative scales ($ \eta $ is the Kolmogorov scale). Simulations start from a fully developed field initialized with a spectrum matching Comte-Bellot and Corrsin’s experimental data and evolve within a time interval where turbulence exhibits established isotropic decay characteristics. Existing correction models, predominantly based on equilibrium turbulence assumptions, fail to accurately represent the non-equilibrium dynamics governed by large-scale structures. According to the generalized von Kármán spectrum model, we use a correction framework to explain the unresolved low-wavenumber contributions in homogeneous isotropic decaying turbulence. The DNS data reveal that the uncorrected integral scale $ {L}_{{\mathrm{m}}} $ significantly underestimates the true $ L $, with errors escalating as $ {k}_{L}/{k}_{p} $ increases, where $ {k}_{L} $ is the minimum resolvable wavenumber in the simulation domain. After correction, $ L $ exhibits a temporal evolution following the Saffmann-predicted power-law relationship $ L\propto {t}^{2/5} $, contrasting sharply with the underestimated pre-correction values. Although the spectral correction substantially increases the spectral integral scale $ L $, its value remains less than the physically derived integral scale $ \varLambda $ computed from the velocity correlation function, which is primarily due to the finite domain size limiting large-scale statistics and the moderate grid resolution, though higher-resolution simulations with the same domain show $ L $ converging towards $ \varLambda $. Notably, the unmodified dissipation coefficient $ {C}_{\varepsilon } $ remains constant, which is consistent with equilibrium turbulence assumptions, whereas the corrected $ {C}_{\varepsilon } $ evolves according to the non-equilibrium scaling law $ {C}_{\varepsilon }\sim{Re}_{\varLambda }^{-1} $. Further analysis confirms that the ratio $ L/\varLambda $ shifts from Kolmogorov’s $ {Re}_{\varLambda }^{1} $dependence to a Reynolds-number-independent plateau after correction, fundamentally changing the turbulence dissipation paradigm. This transition from equilibrium to non-equilibrium dissipation behavior underscores the dominant role of large-scale structures in regulating energy cascade dynamics. Our results demonstrate that finite Reynolds numbers or strong initial-condition effects amplify the non-equilibrium characteristics of turbulence, hindering the full-scale equilibrium. These findings reconcile long-standing theoretical discrepancies and provide a paradigm for modeling scale interactions in turbulence.
-
Keywords:
- isotropic turbulence /
- integral length scale /
- low-wavenumber deficiency /
- von Kármán spectrum model
-
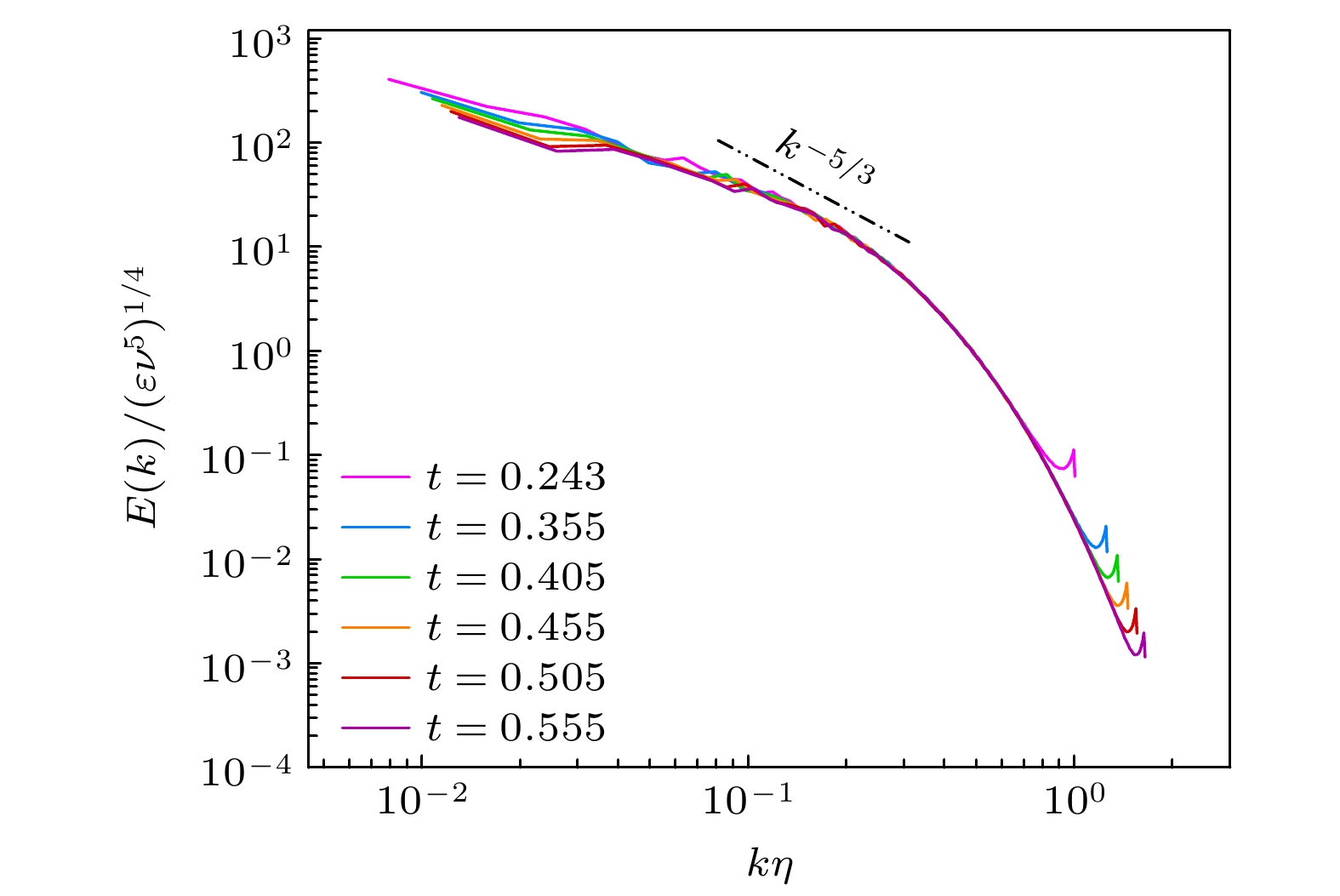
图 1 算例能谱$ E\left(k\right) $随波数的演化. 其中能谱$ E\left(k\right) $用湍动能耗散率$ \text{e} $和运动黏度$ \text{n} $无量纲化, 波数$ k $用耗散尺度$ \text{h} $无量纲化. 双点划线满足$ E\left(k\right)\sim{k}^{-5/3} $关系. 能谱在惯性子区满足$ {k}^{-5/3} $标度律
Figure 1. Example of the energy spectrum $ E\left(k\right) $ evolution with wavenumber. The energy spectrum $ E\left(k\right) $ is non-dimensionalized by the turbulent kinetic energy dissipation rate $ \varepsilon $ and the kinematic viscosity $ \text{n} $, while the wavenumber $ k $ is non-dimensionalized by the dissipation scale $ \text{h} $. The double dot-dash line corresponds to the $ E\left(k\right)\sim $$ {k}^{-5/3} $ relationship. The energy spectrum in the inertial subrange follows the $ {k}^{-5/3} $ scaling law.
图 2 频谱指数$ p $及低波数缺失程度$ {k}_{L}/{k}_{p} $对统计参数修正的影响 (a) 对$ {u}^{2} $的影响; (b) 对$ L $的影响
Figure 2. Effects of spectral exponent $ p $ and low-wavenumber deficiency ratio $ {k}_{L}/{k}_{p} $ on statistical parameters: (a) Impact on $ u $; (b) impact on $ L $.
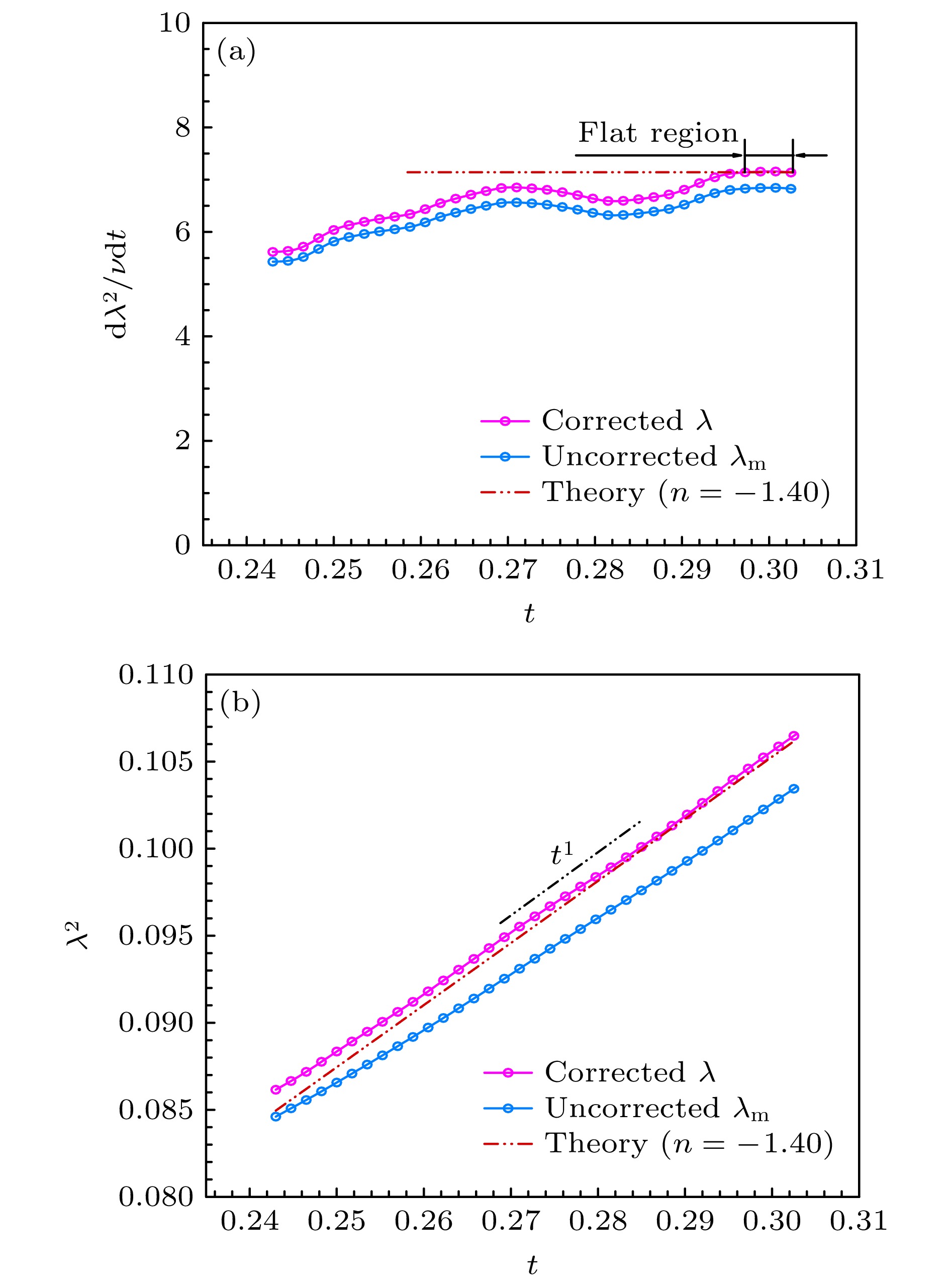
图 3 泰勒尺度随时间的演化特征 (a) 泰勒尺度平方的时间导数, 曲线在$ t > 0.29725 $后呈现平坦特征, 双点划线为$ n=-1.40 $理论线; (b) 泰勒尺度平方, 双点划线满足$ {\varLambda }^{2}\sim{t}^{1} $关系
Figure 3. Evolution characteristics of the Taylor scale over time: (a) Time derivative of the Taylor scale squared. The curve exhibits a flat characteristic for $ t > 0.29725 $, with the double dot-dash line representing the theoretical line $ n=-1.40 $; (b) Taylor scale squared. The double dot-dash line corresponds to the $ {\varLambda }^{2}\sim{t}^{1} $ relationship.
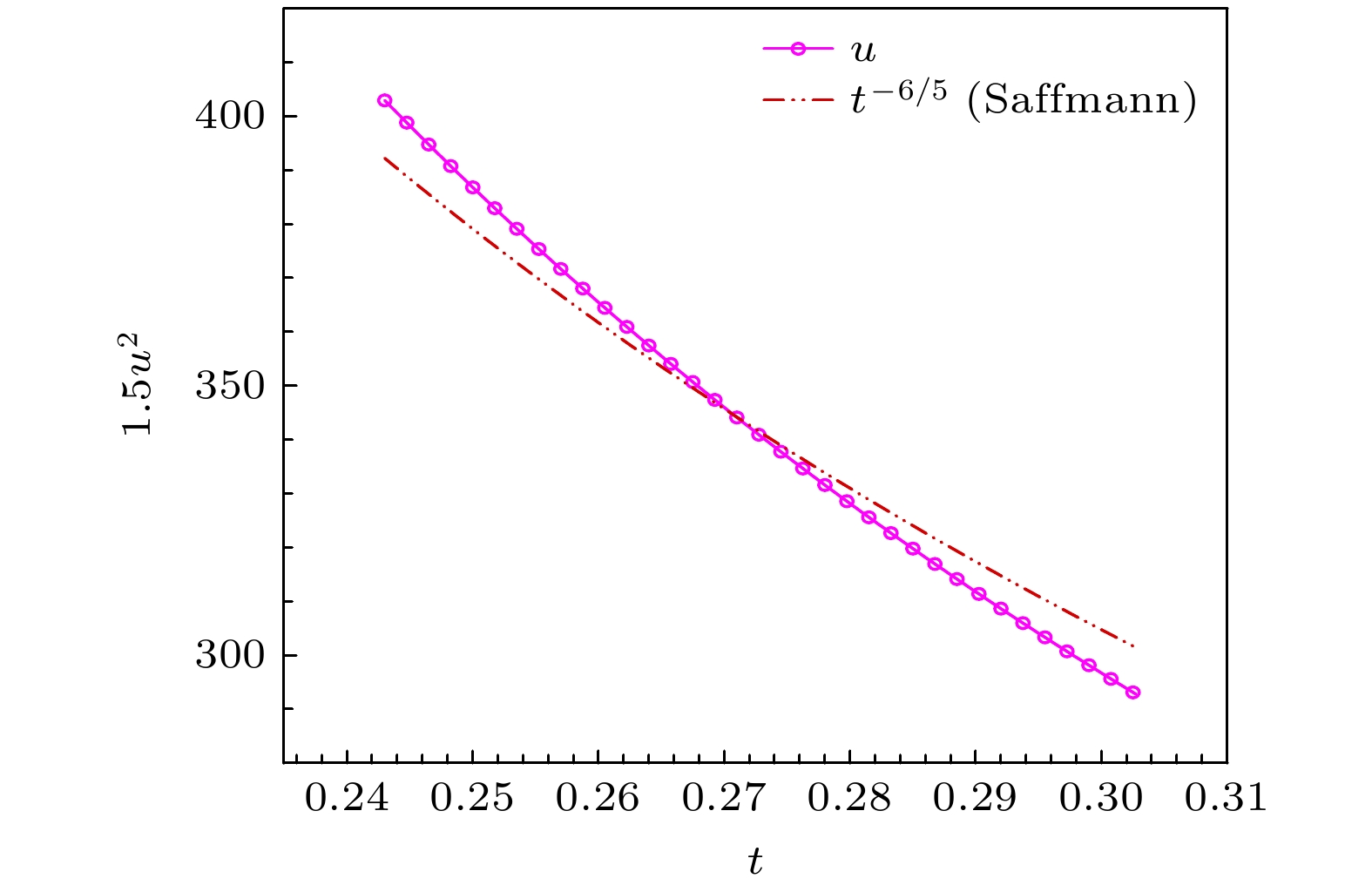
图 4 湍动能随时间演化. 双点划线满足$ {u}^{2}\sim{t}^{-6/5} $关系. 已知修正前后$ {u}^{2} $变化很小, 所以只做修正后的湍动能曲线
Figure 4. Evolution of turbulent kinetic energy over time. The double dot-dash line corresponds to the $ {u}^{2}\sim{t}^{-6/5} $ relationship. Since the variation in $ {u}^{2} $ before and after correction is negligible, only the corrected turbulent kinetic energy curve is plotted.
图 5 修正前后积分尺度随时间的演化. 双点划线满足$ L\sim $$ t^{2/5} $关系
Figure 5. Evolution of the integral scale before and after correction over time. The double dot-dash line corresponds to the $ L{\sim t}^{1/2} $ relationship.
图 6 积分尺度之比随时间的演化
Figure 6. Evolution of the integral scale ratio with time.
图 7 修正前后耗散系数$ {C}_{\varepsilon } $随泰勒雷诺数$ {Re}_{\varLambda } $的变化. 双点划线满足$ {C}_{\varepsilon }\sim{Re}_{\varLambda }^{-1} $关系. 箭头指示方向为时间演化方向
Figure 7. Variation of the dissipation coefficient $ {C}_{\varepsilon } $ with the Taylor Reynolds number $ {Re}_{\varLambda } $ before and after correction. The double dot-dash line corresponds to the $ {C}_{\varepsilon }\sim{Re}_{\varLambda }^{-1} $ relationship. The arrows indicate the direction of time evolution.
图 8 修正前后特征尺度$ L/\varLambda $比值随泰勒雷诺数$ {Re}_{\varLambda } $的演化. 双点划线满足$ L/\varLambda \sim{Re}^{1} $关系
Figure 8. Evolution of the characteristic scale ratio $ L/\varLambda $ with the Taylor Reynolds number $ {Re}_{\varLambda } $ before and after correction. The double dot-dash line corresponds to the $ L/\varLambda \sim{Re}^{1} $ relationship.
-
[1] Pope S B 2001 Turbulent flows (Cambridge: Cambridge University Press
[2] Warhaft Z, Lumley J L 1978 J. Fluid Mech. 88 659
Google Scholar
[3] Porté-Agel F, Bastankhah M, Shamsoddin S 2020 Boundary-Layer Meteorol. 174 1
Google Scholar
[4] Trush A, Pospíšil S, Kozmar H 2020 WIT Trans. Eng. Sci. 128 113
[5] Cotela Dalmau J, Oñate Ibáñez de Navarra E, Rossi R 2016 Applications of turbulence modeling in civil engineering (Barcelona: CIMNE
[6] Li M, Li M, Sun Y 2021 J. Sound Vib. 490 115721
Google Scholar
[7] Taylor G I 1935 Proc. R. Soc. London, Ser. A 151 421
Google Scholar
[8] Tennekes H, Lumley J L 1972 A first course in turbulence (Cambridge: MIT Press
[9] Kolmogorov A N 1941 Docl. Akad. Nauk SSSR A 31 538
[10] Dryden H L 1943 Q. Appl. Math. 1 7
Google Scholar
[11] Saffman P G 1967 J. Fluid Mech. 27 581
Google Scholar
[12] Oberlack M 2002 Proc. Appl. Math. Mech. 1 294
Google Scholar
[13] Comte-Bellot G, Corrsin S 1966 J. Fluid Mech. 25 657
Google Scholar
[14] Bos W J T, Shao L, Bertoglio J P 2007 Phys. Fluids 19 045101
Google Scholar
[15] Ishihara T, Morishita K, Yokokawa M, Uno A, Kaneda Y 2016 Phys. Rev. Fluids 1 082403
Google Scholar
[16] Thornber B 2016 Phys. Fluids 28 105107
[17] O’Neill P L, Nicolaides D, Honnery D, Soria J 2004 15th Australasian Fluid Mechanics Conference The University of Sydney, Sydney, Australia, December 13–17, 2004 p1
[18] Ishihara T, Gotoh T, Kaneda Y 2009 Annu. Rev. Fluid Mech. 41 165
Google Scholar
[19] Goto S, Vassilicos J C 2015 Phys. Lett. A 379 1144
Google Scholar
[20] George W K 1992 Phys. Fluids A 4 1492
[21] Liu F, Lu L P, Bos W J T, Fang L 2019 Phys. Rev. Fluids 4 084603
Google Scholar
[22] Wang H, Sonnenmeier J R, Gamard S, George W 2000 International Congress of Theoretical and Applied Mechanics Chicago, IL, August 27–September 1, 2000 p8
[23] de Bruyn Kops S M, Riley J J 1998 Phys. Fluids 10 2125
Google Scholar
[24] Von Karman T 1937 Proc. Natl. Acad. Sci. U. S. A. 23 98
Google Scholar
[25] Rogallo R S 1981 Numerical experiments in homogeneous turbulence (Washington: NASA
[26] Wang C H, Fang L 2018 Chin. Phys. Lett. 35 080501
Google Scholar
[27] Comte-Bellot G, Corrsin S 1966 J. Fluid Mech. 25 657
Google Scholar
[28] Gamard S, George W K 2000 Flow Turbul. Combust. 63 443
Google Scholar
[29] Wang H, George W K 2002 J. Fluid Mech. 459 429
Google Scholar
[30] George W K, Wang H, Wollblad C, Johansson T G 2001 14th Australasian Fluid Mechanics Conference Adelaide University, Adelaide, Australia, December 10–14, 2001 p41
[31] Batchelor G K 1953 The theory of homogeneous turbulence (Cambridge: Cambridge University Press
[32] Bos W J T, Rubinstein R 2017 Phys. Rev. Fluids 2 022601
Google Scholar
[33] Steiros K 2022 Phys. Rev. E 105 035109
[34] Goto S, Vassilicos J C 2016 Phys. Rev. E 94 053108
Google Scholar
[35] Krogstad P Å, Davidson P A 2012 Phys. Fluids 24 035103
Google Scholar
[36] Steiros K 2022 Phys. Rev. Fluids 7 104607
Google Scholar
[37] Vassilicos J C 2015 Annu. Rev. Fluid Mech. 47 95
Google Scholar
[38] Mazellier N, Vassilicos J C 2010 Phys. Fluids 22 075101
Google Scholar
[39] Valente P C, Vassilicos J C 2012 Phys. Rev. Lett. 108 214503
Google Scholar
[40] Liu F, Fang L, Shao L 2020 Chin. Phys. B 29 114702
Google Scholar
DownLoad:
Metrics
- Abstract views: 370
- PDF Downloads: 19
- Cited By: 0
