-
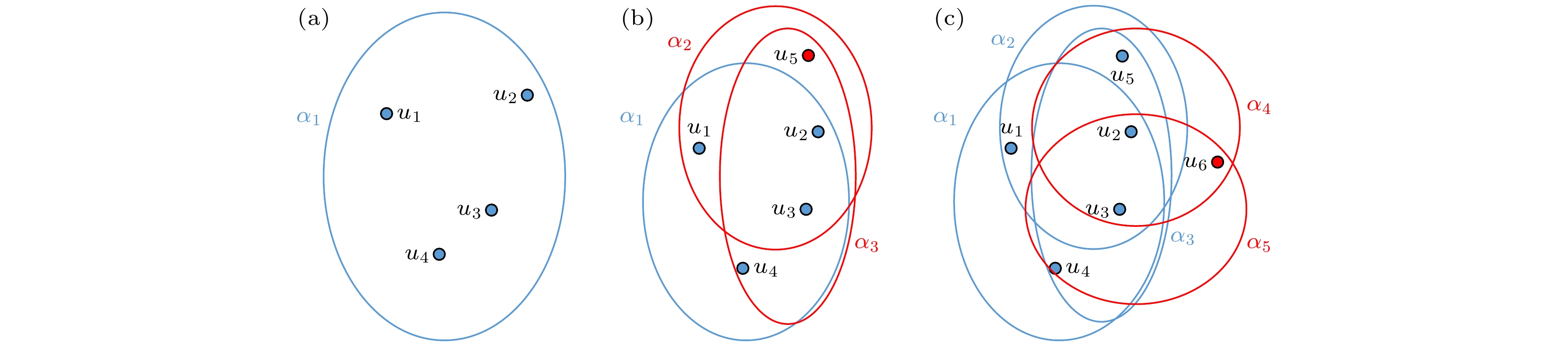
Complex networks are powerful tools for characterizing and analyzing complex systems, with wide applications in fields such as physics, sociology, technology, biology, shipping and port terminal management. One of the core issues in complex networks is the mechanism behind the emergence of scaling laws. In real-world networks, the mechanisms underlying the emergence of scaling laws may be highly complex, making it difficult to design network evolution mechanisms that fully align with reality. Explaining real networks through simple mechanisms is a meaningful research topic. Since Barabási and Albert discovered that growth and linear preferential attachment are mechanisms that generate power-law distributions, scholars have identified various forms of preferential attachment that produce power-law degree distributions. However, the most famous and useful one remains the linear preferential attachment in the BA model. Although complex networks have flourished over the past two decades, they still cannot fully describe real systems with multiple interactions. Hypernetworks, which capture interactions involving more than two nodes, have become an important subject of study, and the mechanisms underlying the emergence of scaling in hypernetworks are a key research focus. The paper first introduces the concept of cliques in hypernetworks. A 1-element clique is a node, a 2-element clique is an edge in a complex network, a 3-element clique represents a triangle in higher-order networks, and a 4-element clique corresponds to a tetrahedron in higher-order networks. Secondly, we propose a clique-driven random hypernetwork evolution model. Using Poisson process theory, we analyze the hypernetwork evolution model, avoiding arbitrary assumptions about node interarrival time distributions commonly made in traditional network analysis, thereby making the network analysis more rigorous. We derive an approximate expression for the cumulative degree distribution and the power-law exponent of the node degree distribution. Finally, we validate the theoretical predictions through computer simulations and empirical analysis of collected real-world data. In our model, not only do nodes join the network in continuous time, but new nodes also randomly select d-element cliques, resulting in a power-law degree distribution. We can estimate the power-law exponent of the model's degree distribution using the number of elements of the driving clique.
-
Keywords:
- complex network /
- hypernetwork /
- higher-order network /
- hypergraph /
- simplicial complex
[1] Redner S 1998 Euro. Phys. J. B 4 131
 Google Scholar
Google Scholar
[2] Kumar R, Raghavan P, Rajalopagan S, Tomkins A 1999 Proceedings of the 9th ACM Symposium on Principles of Database Systems 1
[3] Faloutsos M, Faloutsos P, Faloutsos C 1999 Proc. ACM SIGCOMM, Comput. Commun. Rev. 29 251
 Google Scholar
Google Scholar
[4] Barabási A L, Albert R 1999 Science 286 509
 Google Scholar
Google Scholar
[5] 郭进利 2013 复杂网络和人类行为动力学演化模型(北京: 科学出版社)
Guo J L 2013 Evolving Models of Complex Networks and Human Behavior Dynamics (Beijing: Science Press
[6] 汪小帆, 李翔, 陈关荣 2012 网络科学导论(北京: 高等教育出版社)
Wang X F, Li X, Chen G R 2012 Networks Science: An Introduction (Beijing: Higher Education Press
[7] Boccaletti S, De Lellis P, del Genio C I, Alfaro-Bittner K, Criado R, Jalan S, Romance M 2023 Phys. Rep. 1018 1
 Google Scholar
Google Scholar
[8] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J G, Petri G 2020 Phys. Rep. 874 1
 Google Scholar
Google Scholar
[9] 胡枫, 刘猛, 赵静, 雷蕾 2018 复杂系统与复杂性科学 15 31
Hu F, Liu M, Zhao J, Lei L 2018 Complex Systs. Complexity Sci. 15 31
[10] Zhang K, Gao J Y, Zhao H X, Hu W J, Miao M M, Zhang Z K 2025 Physica A 666 130512
 Google Scholar
Google Scholar
[11] Wang J W, Rong L L, Deng Q H, Zhang J Y 2010 Eur. Phys. J. B 77 493
 Google Scholar
Google Scholar
[12] 胡枫, 赵海兴, 马秀娟 2013 中国科学: 物理学 力学 天文学 43 16
Hu F, Zhao H X, Ma X J 2013 Sci. Sin. Phys. Mech. Astron. 43 16
[13] 郭进利, 祝昕昀 2014 物理学报 63 090207
 Google Scholar
Google Scholar
Guo J L, Zhu X Y 2014 Acta Phys. Sin. 63 090207
 Google Scholar
Google Scholar
[14] 胡枫, 赵海兴, 何佳倍, 李发旭, 李淑玲, 张子柯 2013 物理学报 62 198901
 Google Scholar
Google Scholar
Hu F, Zhao H X, He J B, Li F X, Li S L, Zhang Z K 2013 Acta Phys. Sin. 62 198901
 Google Scholar
Google Scholar
[15] Bianconi G 2021 Higher-Order Networks-An Introduction to Simplicial Complexes (London: Cambridge University Press Inc.
[16] Bianconi G, Rahmede C 2016 Phys. Rev. E 93 032315
[17] Fountoulakis N, Iyer T, Mailler C, Sulzbach H 2022 Ann. Appl. Probab. 32 2860
[18] Kovalenko K, Sendiña-Nadal I, Khalil N, Dainiak A, Musatov D, Raigorodskii A M, Alfaro-Bittner K, Barzel B, Boccaletti S 2021 Commun. Phys. 4 1
 Google Scholar
Google Scholar
[19] Courtney O T, Bianconi G 2017 Phys. Rev. E 93 062311
[20] Bian J H, Zhou T, Bi Y L 2025 Commun. Phys. 8 228
 Google Scholar
Google Scholar
[21] Bianconi G 2024 J. Phys. A: Math. Theor. 57 015001
 Google Scholar
Google Scholar
[22] 张科, 高靖宇, 胡文军, 张永 2023 中国科学: 物理学 力学 天文学 53 270511
 Google Scholar
Google Scholar
Zhang K, Gao J W, Hu W J, Zhang Y 2023 Sci. Sin. Phys. Mech. Astron. 53 270511
 Google Scholar
Google Scholar
[23] 周涛, 肖伟科, 任捷, 汪秉宏 2007 复杂系统与复杂性科学 4 10
Zhou T, Xiao W K, Ren J, Wang B H 2007 Complex Systs. Complexity Sci. 4 10
[24] Bretto A 2013 Hypergraph Theory (Switzerland: Springer International Publishing Switzerland
[25] Barabási A L, Albert R, Jeong H 1999 Physica A 272 173
 Google Scholar
Google Scholar
-
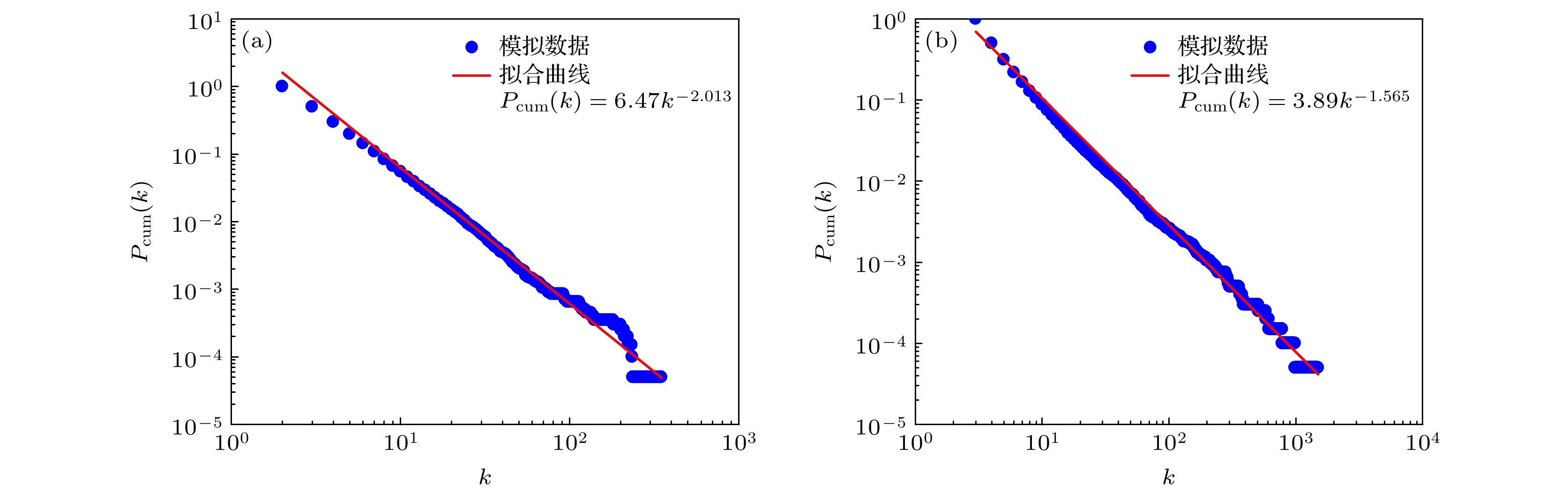
图 2 模型的累积度分布与回归曲线, 横轴是度, 纵轴是累积度分布$ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right) $ (a) $ d=2, m=1 $时模型的累积度分布与回归曲线, 回归曲线的相关系数$ R=-0.9825 $, 幂律指数$ \tau =2.013 $; (b) $ d=3, m=1 $时模型的累积度分布与回归曲线, 回归曲线的相关系数$ R=-0.9934 $, 幂律指数$ \tau =1.565 $
Figure 2. The cumulative degree distribution and regression curve of the model, the horizontal axis represents degrees and the vertical axis represents the cumulative degree distribution $ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right) $: (a) The cumulative degree distribution and regression curve of the model when $ d=2, m=1 $, the correlation coefficient of the regression curve is $ R=-0.9825 $, and the power-law exponent is $ \tau =2.013 $; (b) the cumulative degree distribution and regression curve of the model when $ d=3, m=2 $, the correlation coefficient of the regression curve is:$ R=-0.9934 $, and the power-law exponent is: $ \tau =1.565 $.
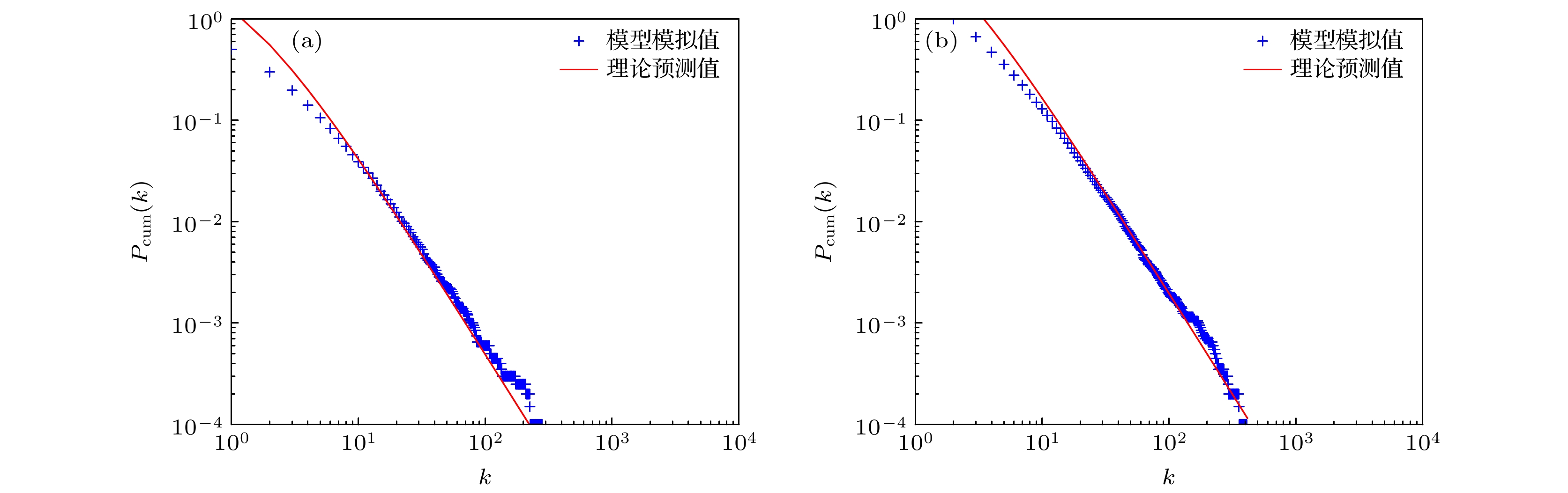
图 3 $ d=2 $时模型的累积度分布与理论预测曲线. 横轴是度, 纵轴是累积度分布$ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right) $, 蓝色+表示模型的模拟值, 红色实线对应于方程(5)给出的理论预测值, 幂律指数为$ \tau =2 $ (a) $ m=1 $时模型的累积度分布模拟值与理论预测曲线; (b) $ m=2 $时模型的累积度分布模拟值与理论预测曲线
Figure 3. The cumulative degree distribution and theoretical prediction curve of the model with $ d=2 $. The horizontal axis represents degrees and the vertical axis represents the cumulative degree distribution $ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right), $ the blue + denotes the simulation value of the model. The red solid line corresponds to the theoretical predicted value given by Eq. (5), and the power-law exponent is $ \tau =2 $: (a) The cumulative degree distribution and theoretical prediction curve of the model when $ m=1 $; (b) the cumulative degree distribution and theoretical prediction curve of the model when $ m=2 $.
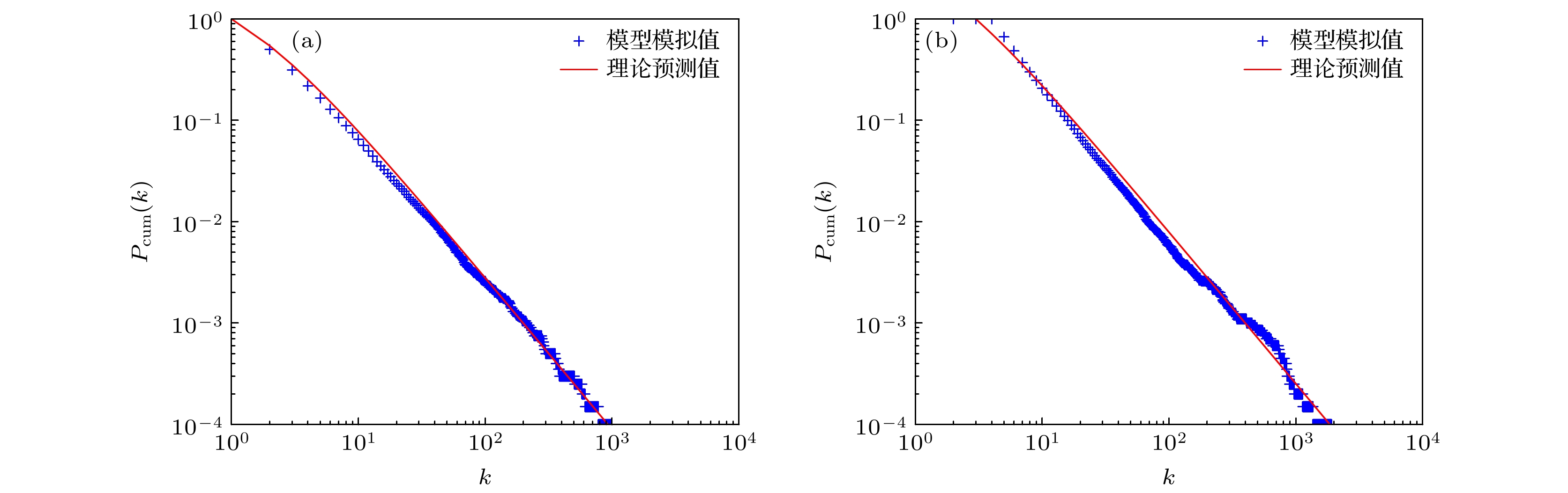
图 4 $ d=3 $时模型的累积度分布与理论预测曲线. 横轴是度, 纵轴是累积度分布$ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right) $, 蓝色+表示模型的模拟值, 红色实线对应于方程(5)给出的理论预测值, 幂律指数为$ \tau =1.5 $, 其余部分与图3相同
Figure 4. The cumulative degree distribution and theoretical prediction curve of the model with $ d=3. $ The horizontal axis represents degrees and the vertical axis represents the cumulative degree distribution $ {P}_{\mathrm{c}\mathrm{u}\mathrm{m}}\left(k\right) $, the blue + denotes the simulation value of the model, the red solid line corresponds to the theoretical predicted value given by Eq. (5), and the power-law exponent is $ \tau =1.5 $, the rest of the caption is the same as that in Fig. 3.
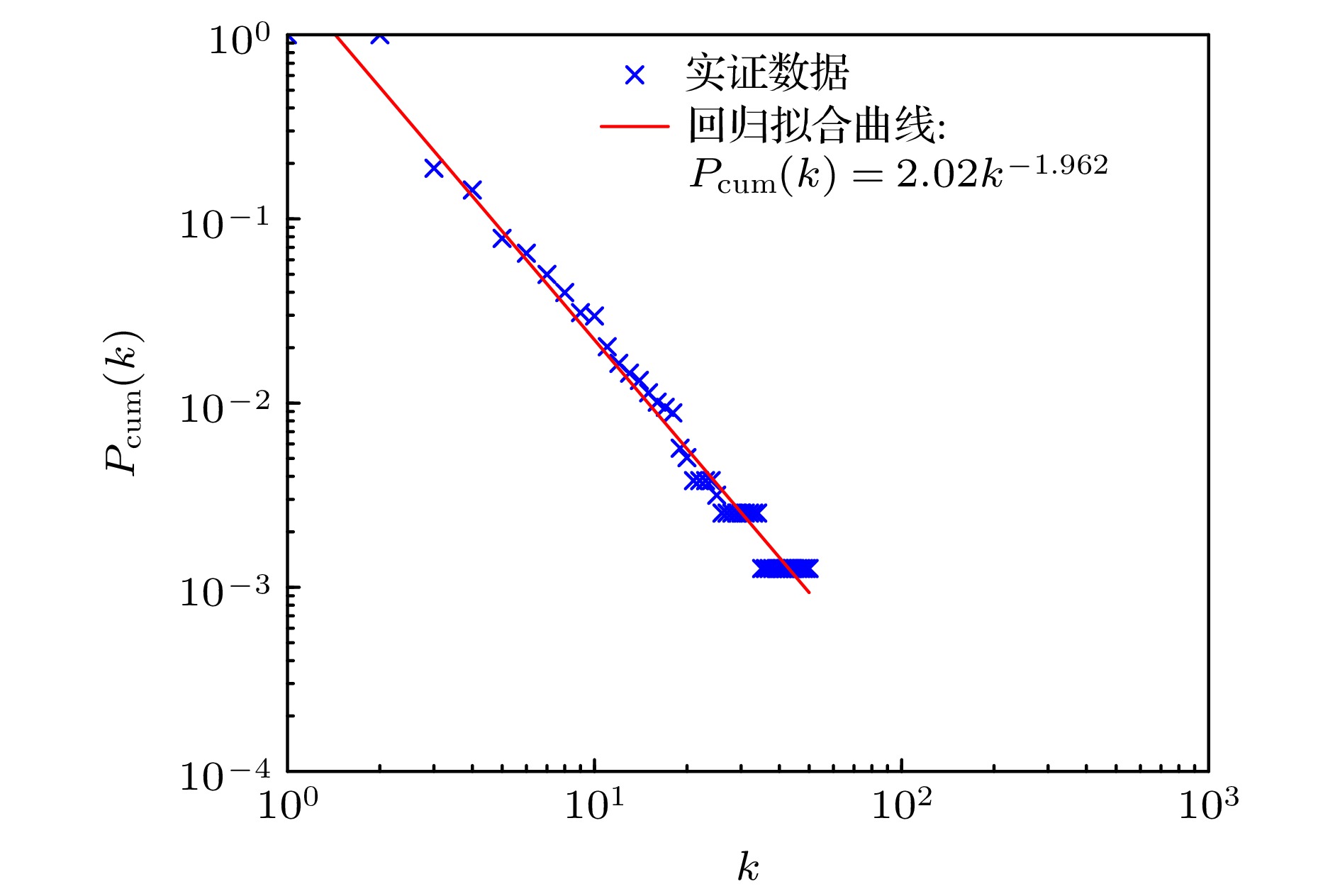
图 5 新能源汽车专利合作超网络的累积度分布, 网络规模N = 1582, 蓝色叉表示新能源汽车专利合作超网络的累积度分布, 红色实线表示回归拟合曲线, 相关系数$ R= $$ -0.9916 $, 累积度分布的幂律指数$ \tau =1.962 $
Figure 5. The cumulative degree distribution of the new energy vehicle patent cooperation hypernetwork, the network scale is N = 1582, the blue cross denotes the cumulative degree distribution of the new energy vehicle patent cooperation hypernetwork, the red solid line represents the regression fitting curve, with a correlation coefficient $ R= $$ -0.9916 $, and the power-law exponent of the cumulative degree distribution is $ \tau =1.962 $.
图 6 下秩3的科学家合作超网络累积度分布. 网络规模N = 1830, 蓝色叉表示下秩3的科学家合作超网络累积度分布. 红色实线表示回归拟合曲线, 相关系数$ R= -0.9766 $, 累积度分布的幂律指数$ \tau =1.88 $
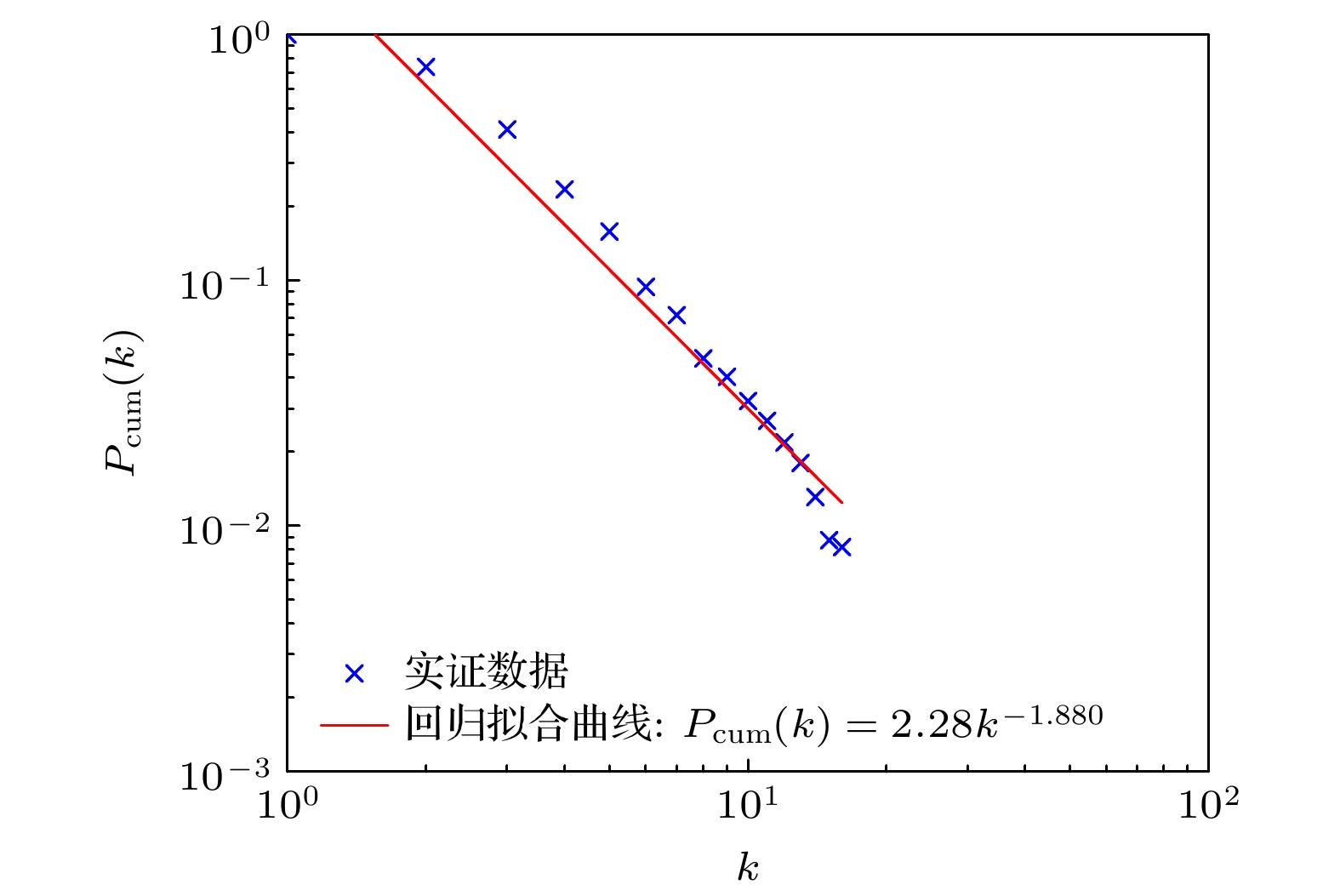
Figure 6. The accumulation degree distribution of the scientist cooperative hypernetwork with the lower rank 3. The network scale is N = 1830, the blue cross denotes the cumulative degree distribution of the hypernetwork. The red solid line represents the regression fitting curve, with a correlation coefficient $ R=-0.9766 $, and the power-law exponent of the cumulative degree distribution is $ \tau =1.88 $.
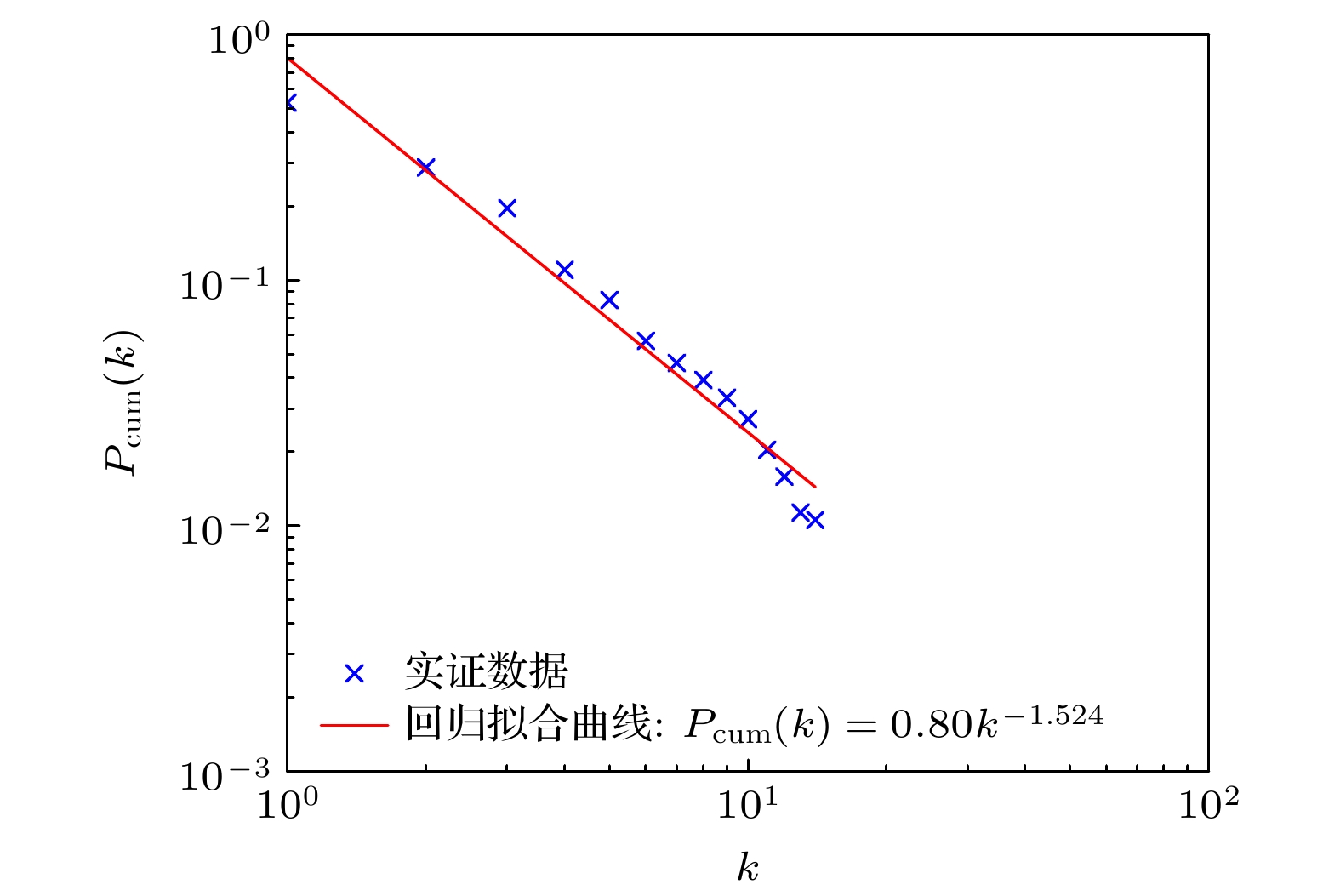
图 7 下秩4的科学家合作超网络累积度分布. 网络规模N = 1342, 蓝色叉表示下秩4的科学家合作超网络累积度分布, 红色实线表示回归拟合曲线, 相关系数$ R= -0.9833 $, 累积度分布的幂律指数$ \tau =1.524 $
Figure 7. The accumulation degree distribution of the scientist cooperative hypernetwork with the lower rank 4. The network scale is N = 1342, the blue cross denotes the cumulative degree distribution of the hypernetwork, the red solid line represents the regression fitting curve, with a correlation coefficient $ R=-0.9833 $, and the power-law exponent of the cumulative degree distribution is $ \tau =1.542 $.
-
[1] Redner S 1998 Euro. Phys. J. B 4 131
 Google Scholar
Google Scholar
[2] Kumar R, Raghavan P, Rajalopagan S, Tomkins A 1999 Proceedings of the 9th ACM Symposium on Principles of Database Systems 1
[3] Faloutsos M, Faloutsos P, Faloutsos C 1999 Proc. ACM SIGCOMM, Comput. Commun. Rev. 29 251
 Google Scholar
Google Scholar
[4] Barabási A L, Albert R 1999 Science 286 509
 Google Scholar
Google Scholar
[5] 郭进利 2013 复杂网络和人类行为动力学演化模型(北京: 科学出版社)
Guo J L 2013 Evolving Models of Complex Networks and Human Behavior Dynamics (Beijing: Science Press
[6] 汪小帆, 李翔, 陈关荣 2012 网络科学导论(北京: 高等教育出版社)
Wang X F, Li X, Chen G R 2012 Networks Science: An Introduction (Beijing: Higher Education Press
[7] Boccaletti S, De Lellis P, del Genio C I, Alfaro-Bittner K, Criado R, Jalan S, Romance M 2023 Phys. Rep. 1018 1
 Google Scholar
Google Scholar
[8] Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, Young J G, Petri G 2020 Phys. Rep. 874 1
 Google Scholar
Google Scholar
[9] 胡枫, 刘猛, 赵静, 雷蕾 2018 复杂系统与复杂性科学 15 31
Hu F, Liu M, Zhao J, Lei L 2018 Complex Systs. Complexity Sci. 15 31
[10] Zhang K, Gao J Y, Zhao H X, Hu W J, Miao M M, Zhang Z K 2025 Physica A 666 130512
 Google Scholar
Google Scholar
[11] Wang J W, Rong L L, Deng Q H, Zhang J Y 2010 Eur. Phys. J. B 77 493
 Google Scholar
Google Scholar
[12] 胡枫, 赵海兴, 马秀娟 2013 中国科学: 物理学 力学 天文学 43 16
Hu F, Zhao H X, Ma X J 2013 Sci. Sin. Phys. Mech. Astron. 43 16
[13] 郭进利, 祝昕昀 2014 物理学报 63 090207
 Google Scholar
Google Scholar
Guo J L, Zhu X Y 2014 Acta Phys. Sin. 63 090207
 Google Scholar
Google Scholar
[14] 胡枫, 赵海兴, 何佳倍, 李发旭, 李淑玲, 张子柯 2013 物理学报 62 198901
 Google Scholar
Google Scholar
Hu F, Zhao H X, He J B, Li F X, Li S L, Zhang Z K 2013 Acta Phys. Sin. 62 198901
 Google Scholar
Google Scholar
[15] Bianconi G 2021 Higher-Order Networks-An Introduction to Simplicial Complexes (London: Cambridge University Press Inc.
[16] Bianconi G, Rahmede C 2016 Phys. Rev. E 93 032315
[17] Fountoulakis N, Iyer T, Mailler C, Sulzbach H 2022 Ann. Appl. Probab. 32 2860
[18] Kovalenko K, Sendiña-Nadal I, Khalil N, Dainiak A, Musatov D, Raigorodskii A M, Alfaro-Bittner K, Barzel B, Boccaletti S 2021 Commun. Phys. 4 1
 Google Scholar
Google Scholar
[19] Courtney O T, Bianconi G 2017 Phys. Rev. E 93 062311
[20] Bian J H, Zhou T, Bi Y L 2025 Commun. Phys. 8 228
 Google Scholar
Google Scholar
[21] Bianconi G 2024 J. Phys. A: Math. Theor. 57 015001
 Google Scholar
Google Scholar
[22] 张科, 高靖宇, 胡文军, 张永 2023 中国科学: 物理学 力学 天文学 53 270511
 Google Scholar
Google Scholar
Zhang K, Gao J W, Hu W J, Zhang Y 2023 Sci. Sin. Phys. Mech. Astron. 53 270511
 Google Scholar
Google Scholar
[23] 周涛, 肖伟科, 任捷, 汪秉宏 2007 复杂系统与复杂性科学 4 10
Zhou T, Xiao W K, Ren J, Wang B H 2007 Complex Systs. Complexity Sci. 4 10
[24] Bretto A 2013 Hypergraph Theory (Switzerland: Springer International Publishing Switzerland
[25] Barabási A L, Albert R, Jeong H 1999 Physica A 272 173
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 1068
- PDF Downloads: 31
- Cited By: 0














 DownLoad:
DownLoad: