Nonlinear physics
编者按
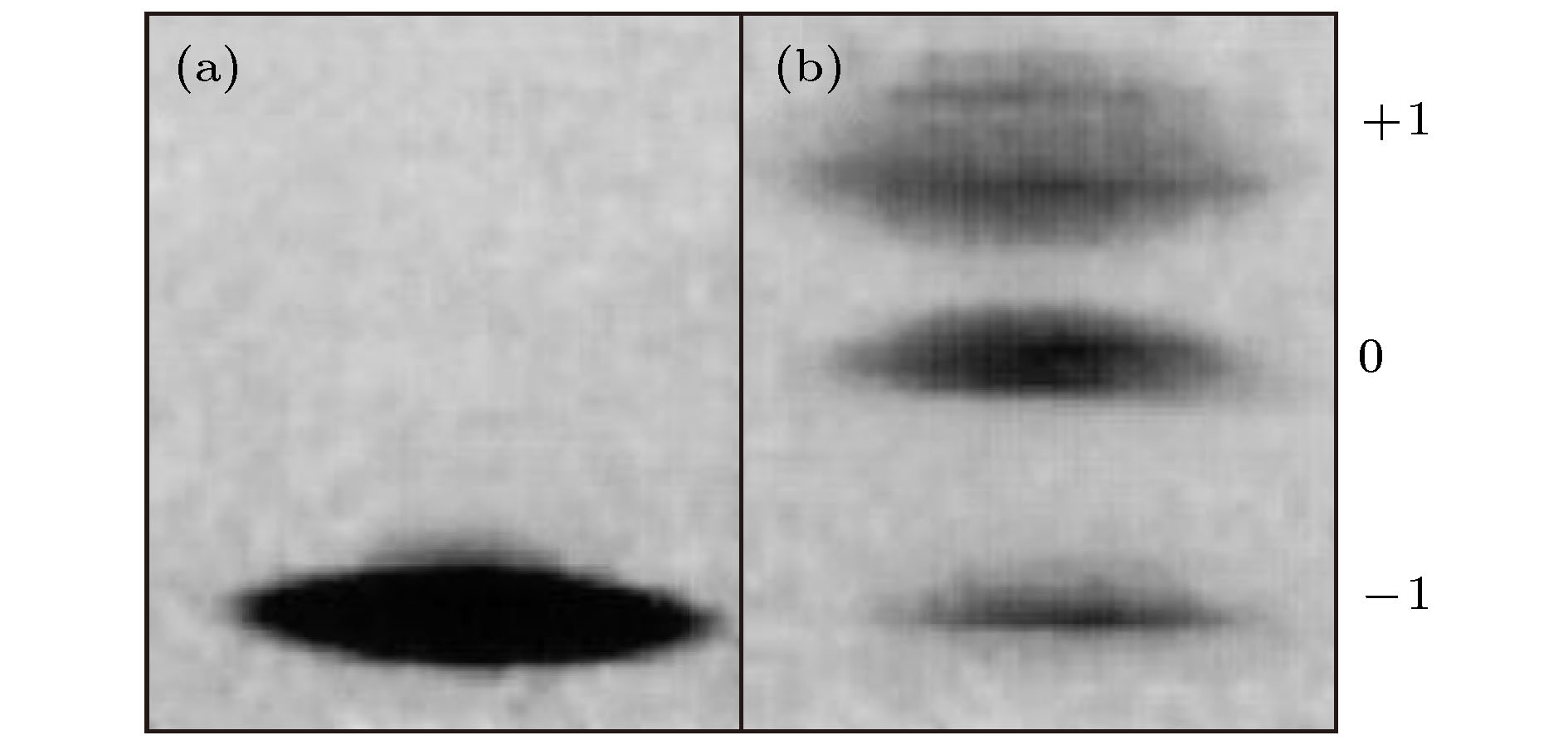
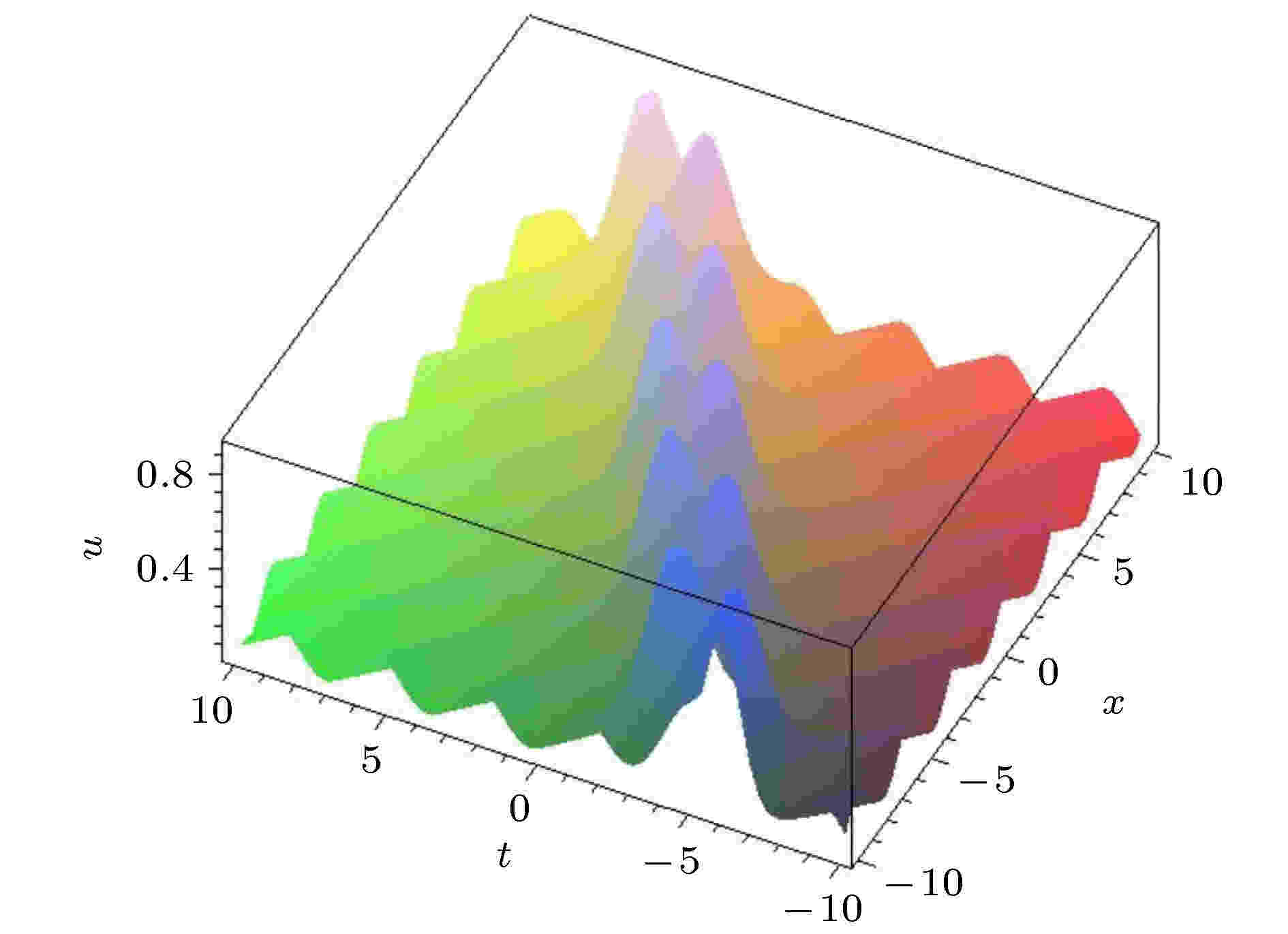
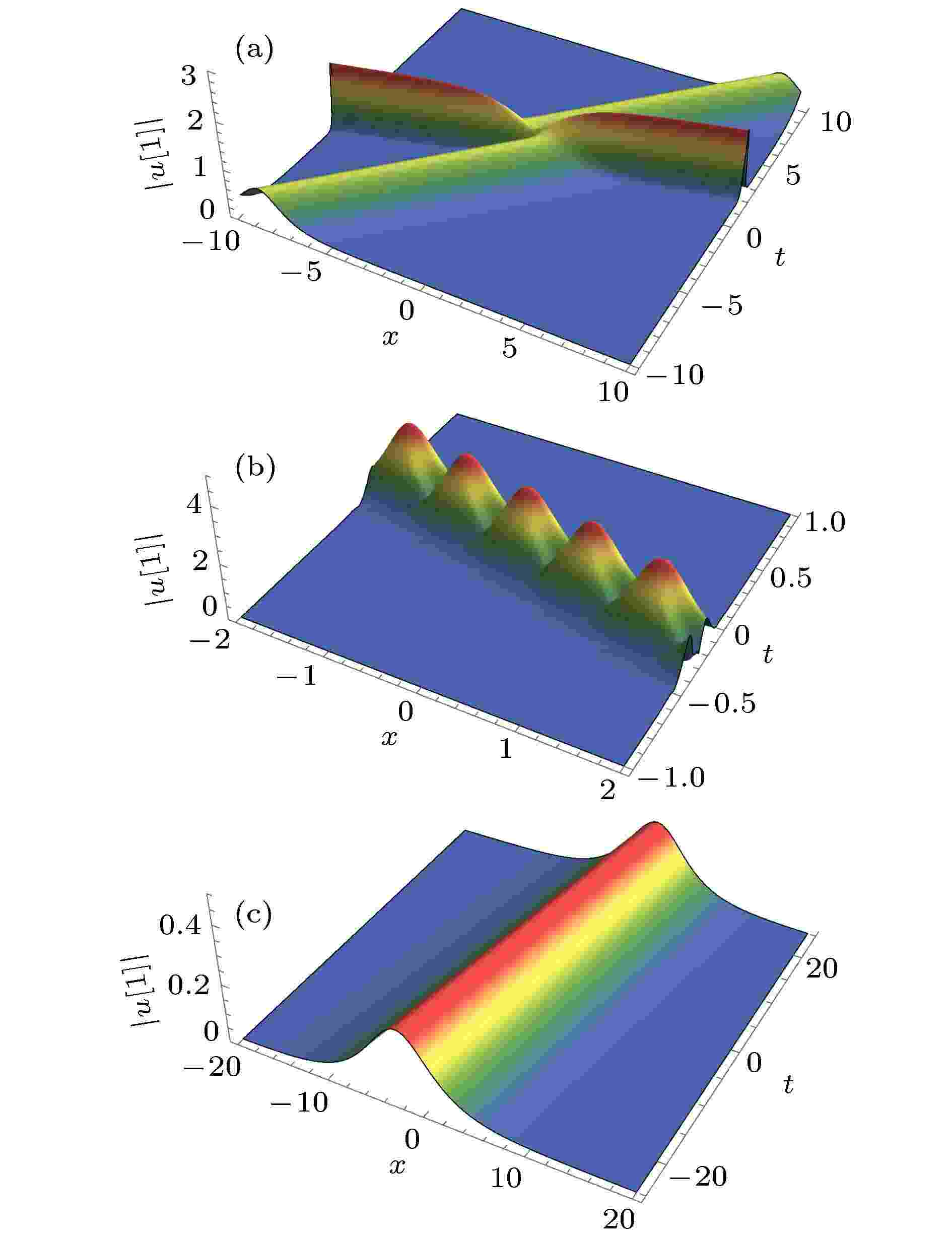
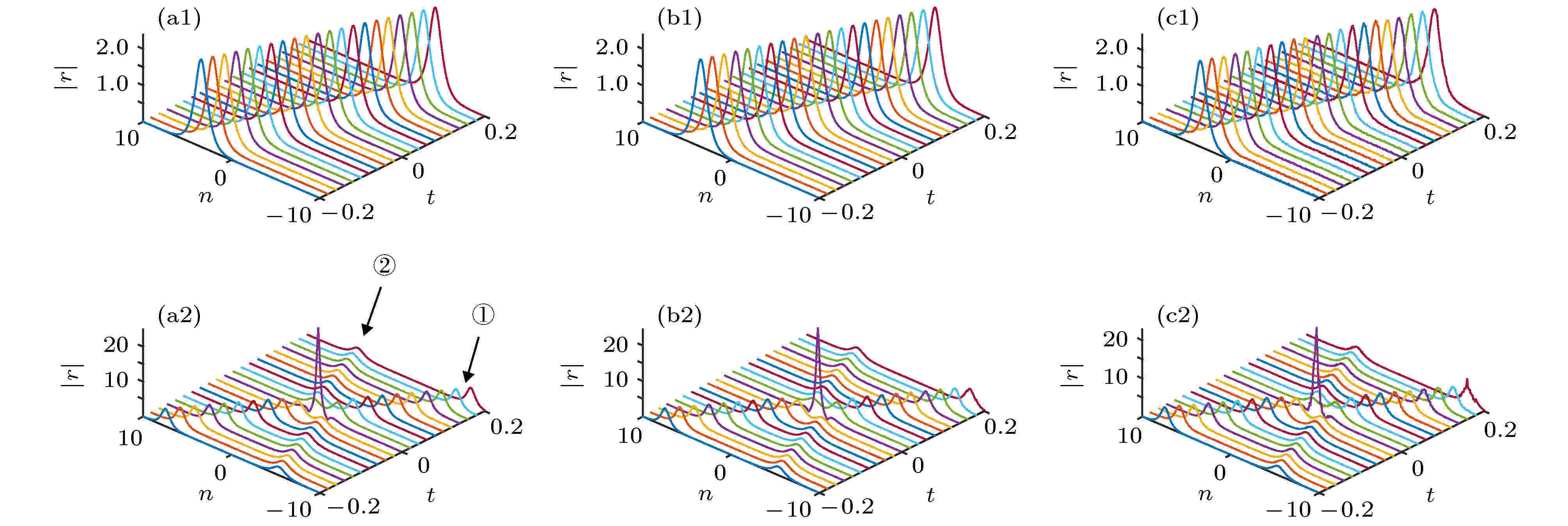
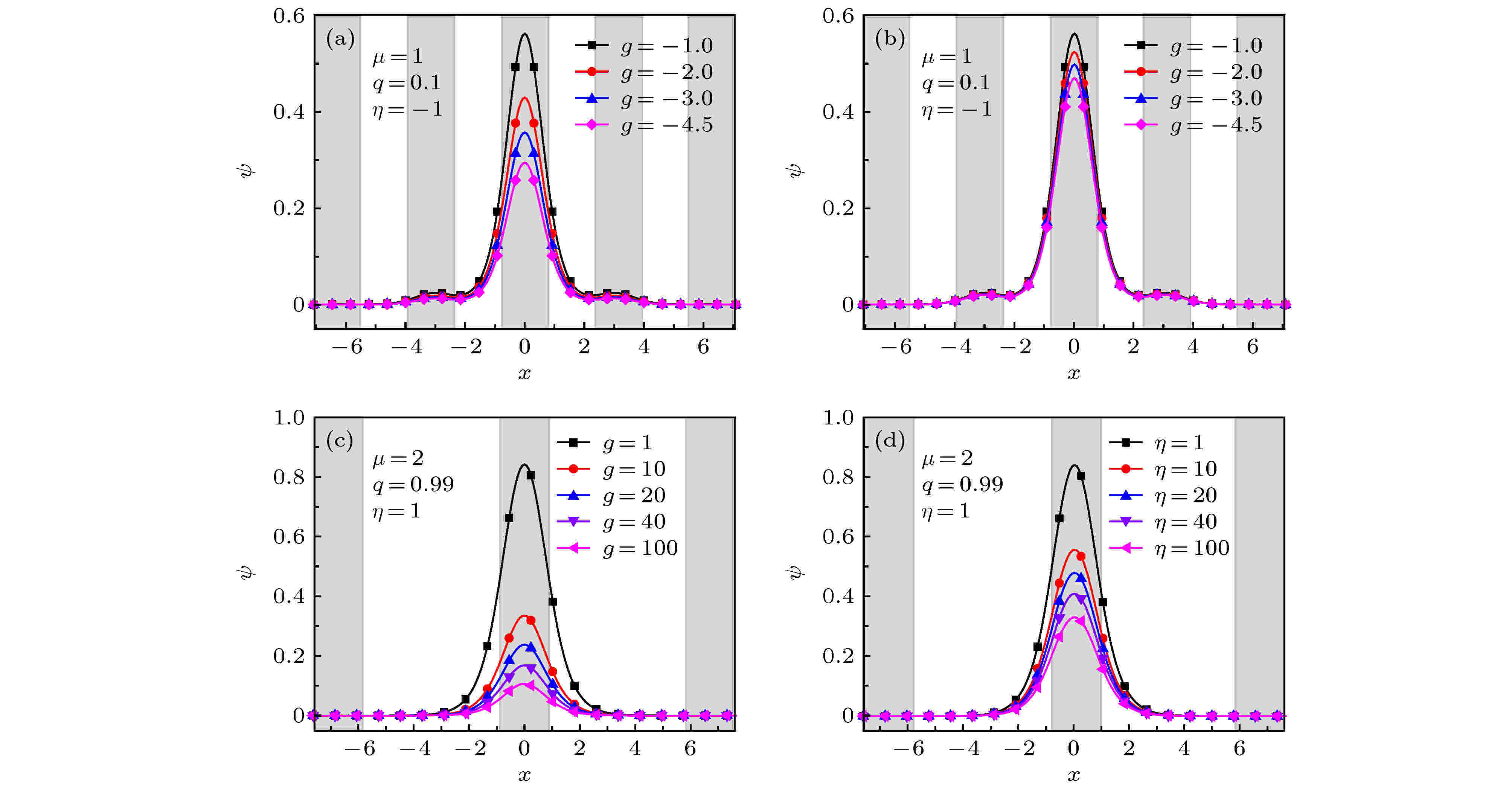
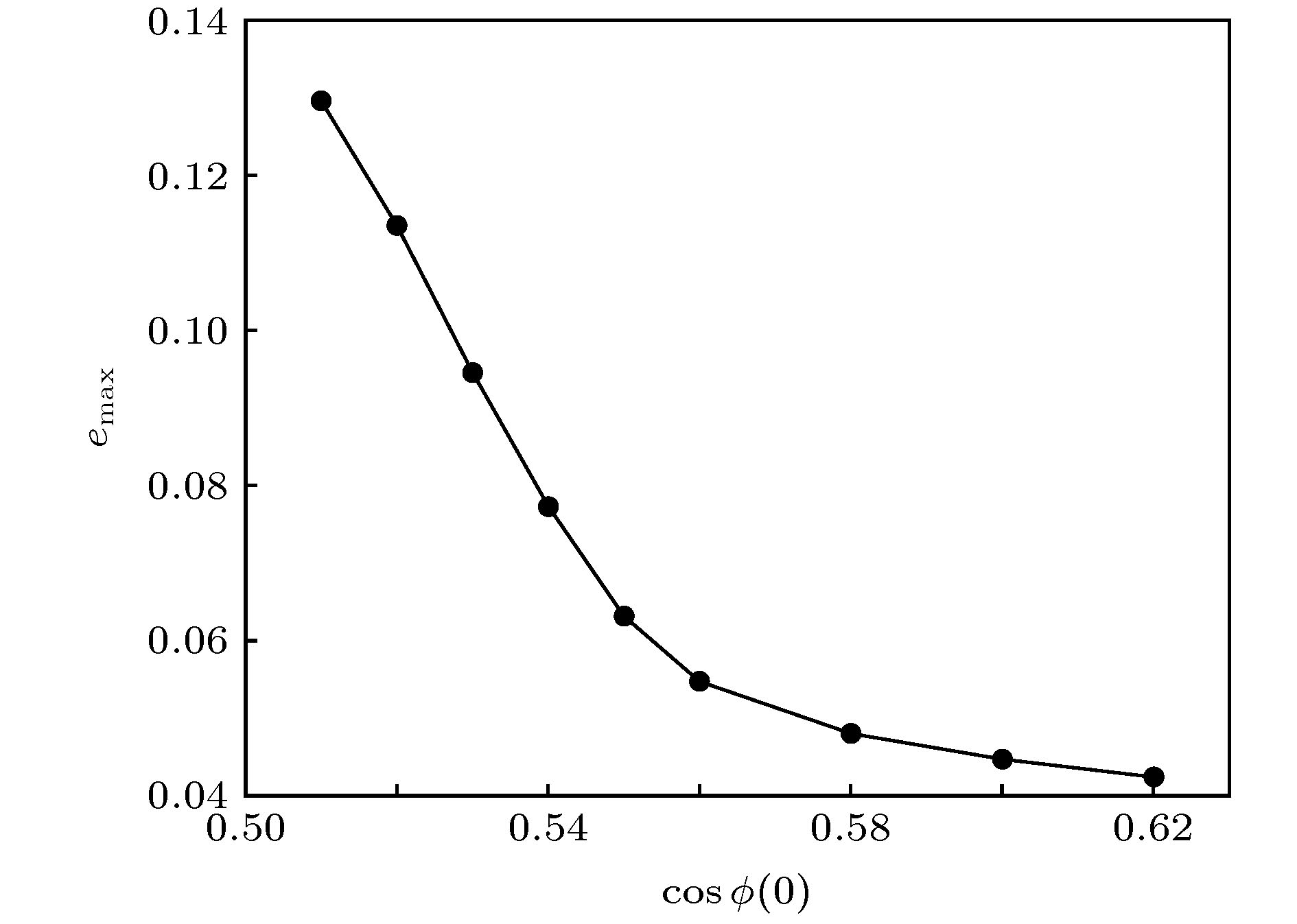
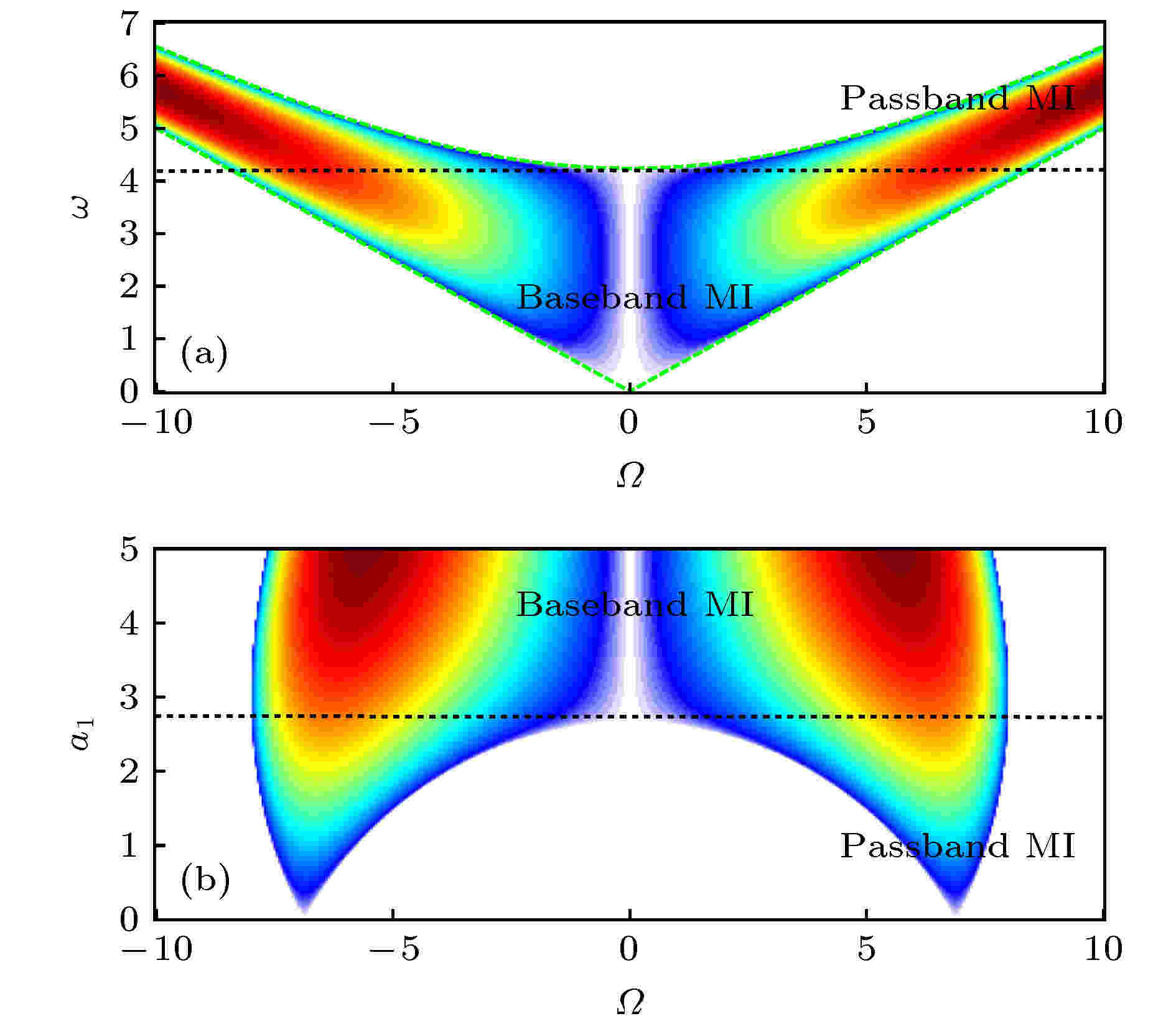
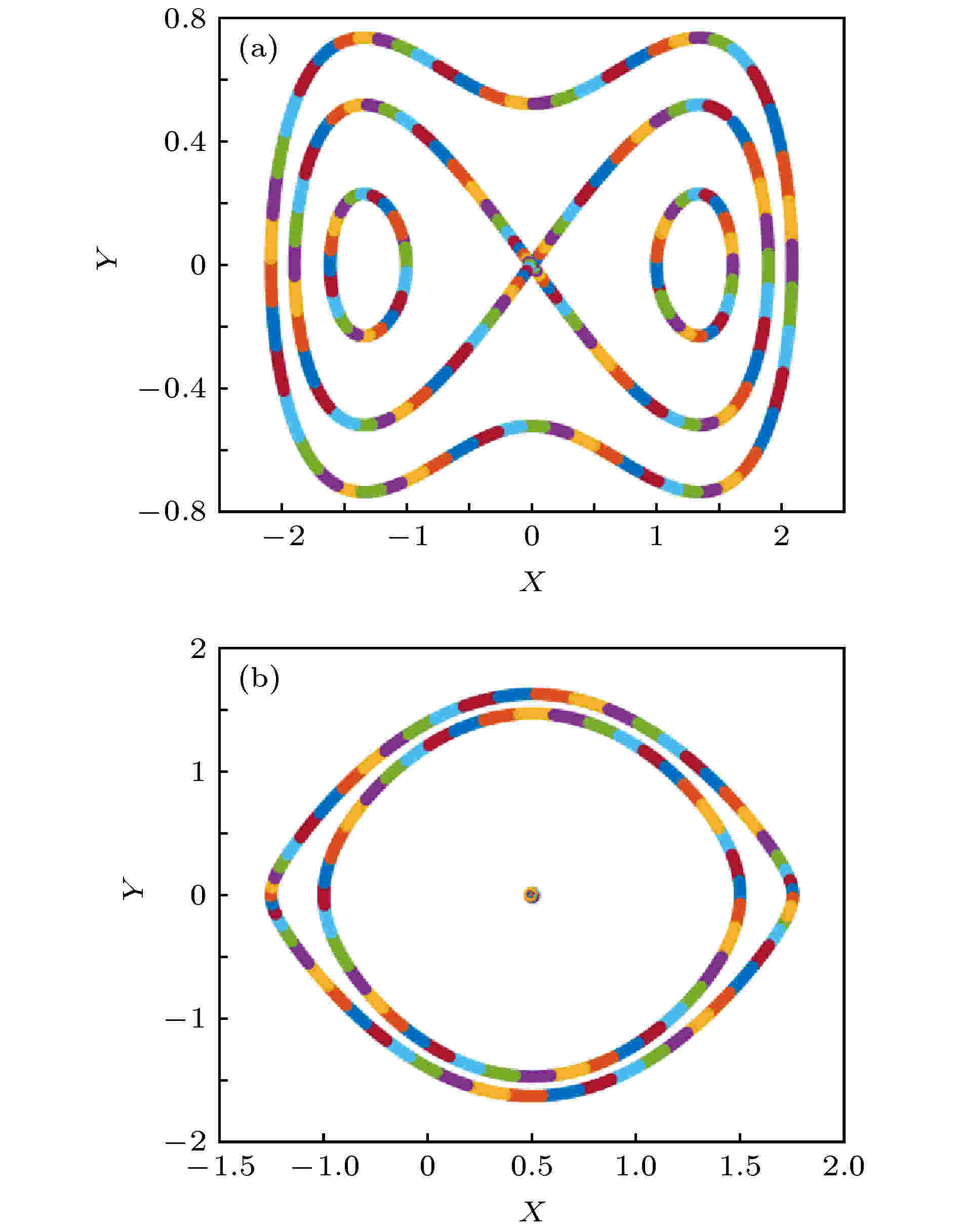
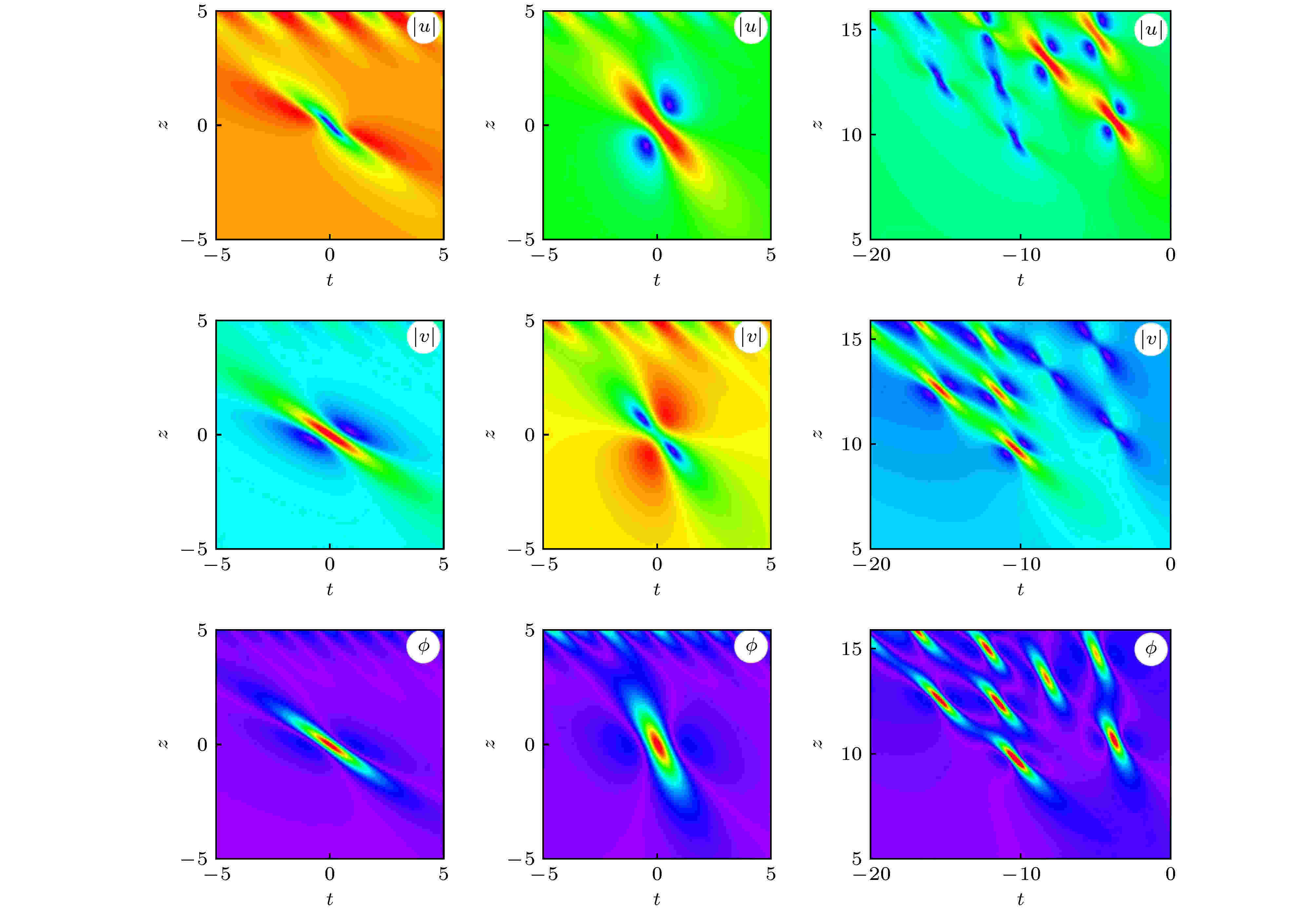
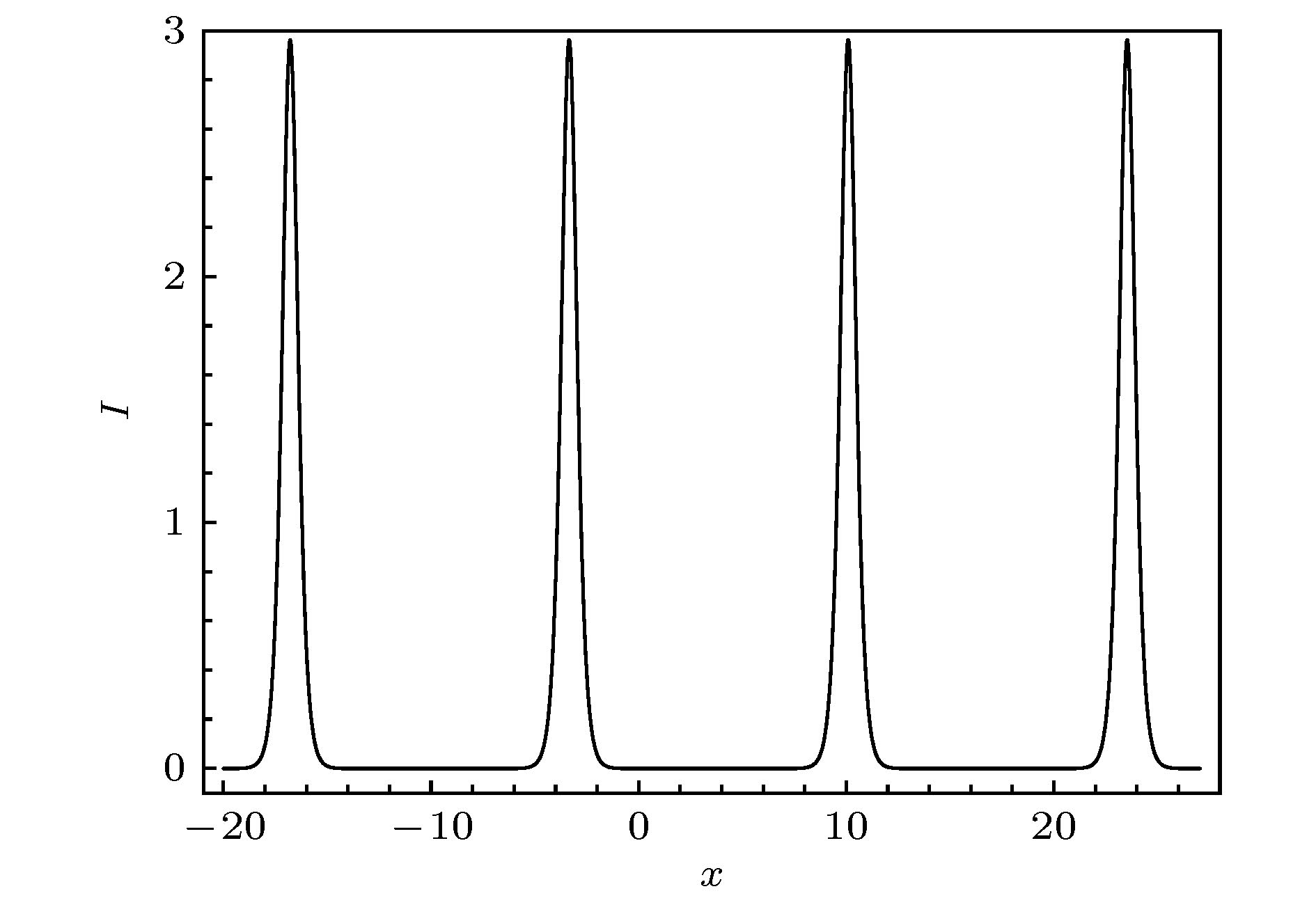
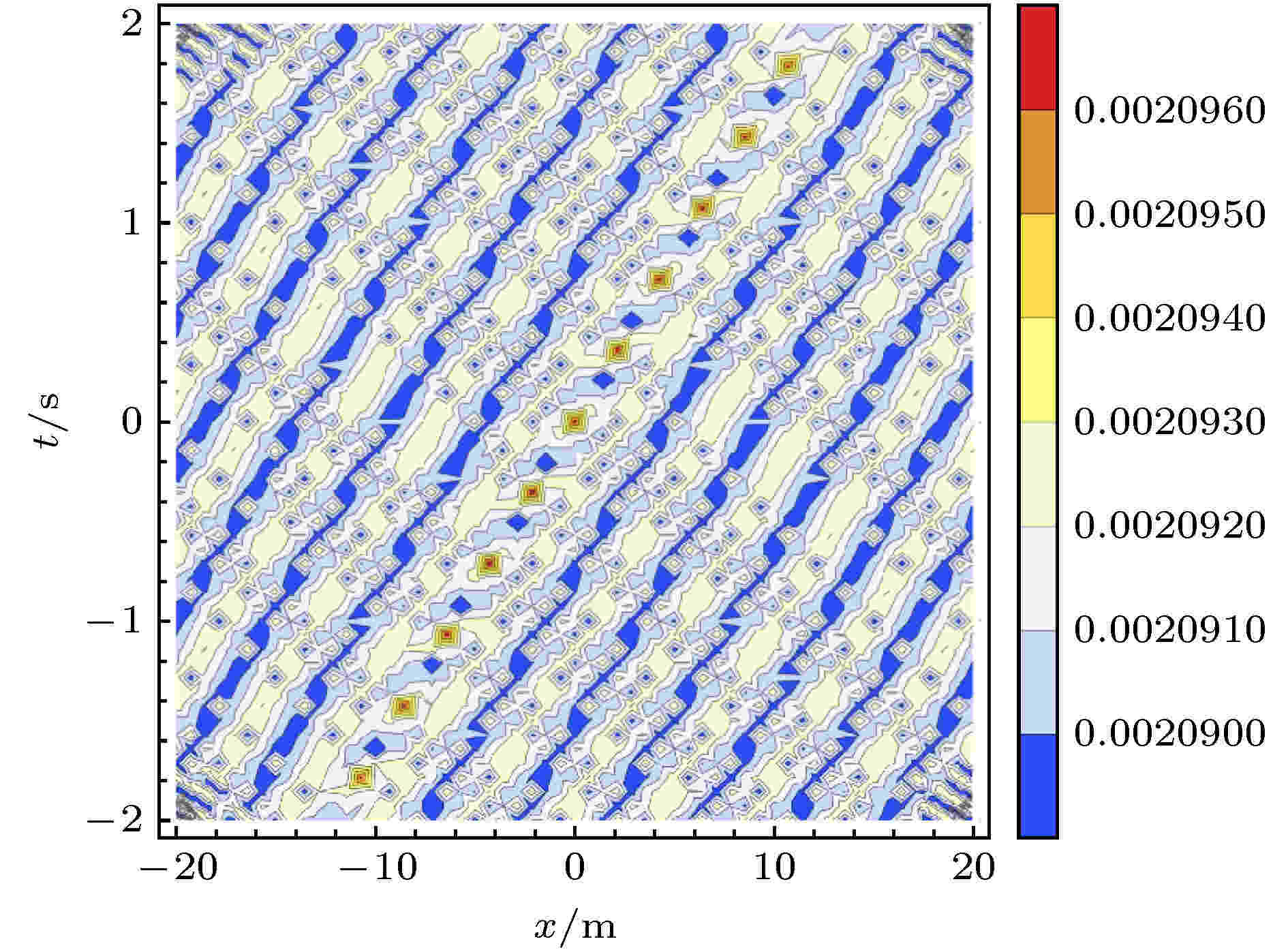
非线性波是非线性物理中常见的现象. 研究非线性波有助于弄清物理系统在非线性作用下的运动变化规律, 合理解释相关的自然现象. 由于非线性波不满足物理学中常用的线性叠加原理, 同时非线性波的控制方程往往是非线性偏微分方程, 这导致对它的研究一直是数学和物理中重要而困难的课题. 近十年来, 由于观测技术的进步, 玻色-爱因斯坦凝聚 (BEC) 系统中孤立子和光纤系统中怪波的实验研究取得了重要进展, 极大地推动了不同物理系统中非线性波及其相关问题的研究. 本专题邀请国内活跃在非线性物理研究第一线的专家撰文 15 篇 (含综述和研究论文), 内容包括从物理角度研究 BEC 系统的拓扑性质和孤立子、铁磁纳米线的磁怪波和弹性管中怪波、光学系统中的怪波和孤立子及其发生机制, 以及从数学角度 (可积系统) 研究非局域系统的孤立子、离散物理系统的多维相容和非线性波、Boussinesq 系统 Lax 对等性质等.
希望本专题能够尽可能反映基于可积系统的非线性波研究现状, 为青年学者选择科研方向、确定研究课题以及从事相关领域研究的人员提供一点帮助, 促进我国在非线性波的物理应用和数学理论的发展.
2020, 69 (1): 010303.
doi: 10.7498/aps.69.20191648
Abstract +
Most of the atoms that realize Bose-Einstein condensation have internal spin degree of freedom. In the optical potential trap, the internal spin of the atom is thawed, and the atom can be condensed into each hyperfine quantum state to form the spinor Bose-Einstein condensate. Flexible spin degrees of freedom become dynamic variables related to the system, which can make the system appear novel topological quantum states, such as spin domain wall, vortex, magnetic monopole, skymion, and so on. In this paper, the experimental and theoretical study of spinor Bose-Einstein condensation, the types of topological defects in spinor Bose-Einstein condensate, and the research progress of topological defects in spinor two-component and three-component Bose-Einstein condensate are reviewed.
2020, 69 (1): 010202.
doi: 10.7498/aps.69.20191647
Abstract +
In contrast to the well-established theory of differential equations, the theory of difference equations has not quite developed so far. The most recent advances in the theory of discrete integrable systems have brought a true revolution to the study of difference equations. Multidimensional consistency is a new concept appearing in the research of discrete integrable systems. This property, as an explanation to a type of discrete integrability, plays an important role in constructing the Bäcklund transformations, Lax pairs and exact solutions for discrete integrable system. In the present paper, the multidimensional consistency and its applications in the research of discrete integrable systems are reviewed.
2020, 69 (1): 010203.
doi: 10.7498/aps.69.20191316
Abstract +
The Boussinesq equation is a very important equation in fluid mechanics and some other disciplines. A Lax pair of the Boussinesq equation is proposed. With the help of the truncated Painlevé expansion, auto-Bäcklund transformation of the Boussinesq equation and Bäcklund transformation between the Boussinesq equation and the Schwarzian Boussinesq equation are demonstrated. Nonlocal symmetries of the Boussinesq equation are discussed. One-parameter subgroup invariant solutions and one-parameter group transformations are obtained. The consistent Riccati expansion solvability of the Boussinesq equation is proved and some interaction structures between soliton-cnoidal waves are obtained by consistent Riccati expansion.
2020, 69 (1): 010204.
doi: 10.7498/aps.69.20191887
Abstract +
In this paper, we introduce an integrable reverse space-time nonlocal Sasa-Satsuma equation. The Darboux transformation and soliton solutions for this nonlocal integrable equation are constructed.
2020, 69 (1): 010205.
doi: 10.7498/aps.69.20191235
Abstract +
It is an important research topic to study diverse local wave interaction phenomena in nonlinear evolution equations, especially for the semi-discrete nonlinear lattice equations, there is little work on their diverse local wave interaction solutions due to the complexity and difficulty of research. In this paper, a semi-discrete higher-order Ablowitz-Ladik equation is investigated via the generalized $(M, N-M)$ -fold Darboux transformation. With the aid of symbolic computation, diverse types of localized wave solutions are obtained starting from constant and plane wave seed background. Particularly, for the case $M=N$ , the generalized $(M, N-M)$ -fold Darboux transformation may reduce to the N-fold Darboux transformation which can be used to derive multi-soliton solutions from constant seed background and breather solutions from plane wave seed background, respectively. For the case $M=1$ , the generalized $(M, N-M)$ -fold Darboux transformation reduce to the generalized $(1, N-1)$ -fold one which can be used to obtain rogue wave solutions from plane wave seed background. For the case $M=2$ , the generalized $(M, N-M)$ -fold Darboux transformation reduce to the generalized $(2, N-2)$ -fold one which can be used to give mixed interaction solutions of one-breather and first-order rogue wave from plane wave seed background. To study the propagation characteristics of such localized waves, the numerical simulations are used to explore the dynamical stability of such obtained solutions. Results obtained in the present work may be used to explain related physical phenomena in nonlinear optics and relevant fields.
2020, 69 (1): 010301.
doi: 10.7498/aps.69.20191278
Abstract +
We study the gap solitons and their stability properties in a Bose-Einstein condensation (BEC) under three-body interaction loaded in a Jacobian elliptic sine potential, which can be described by a cubic-quintic Gross-Pitaevskii equation (GPE) in the mean-field approximation. Firstly, the GPE is transformed into a stationary cubic-quintic nonlinear Schrödinger equation (NLSE) by the multi-scale method. A class of analytical solution of the NLSE is presented to describe the gap solitons. It is shown analytically that the amplitude of the gap soliton decreases as the two-body or three-body interaction strength increases. Secondly, many kinds of gap solitons, including the fundamental soliton and the sub-fundamental soliton, are obtained numerically by the Newton-Conjugate-Gradient (NCG) method. There are two families of fundamental solitons: one is the on-site soliton and the other is the off-site soliton. All of them are bifurcated from the Bloch band. Both in-phase and out-phase dipole solitons for off-site solitons do exist in such a nonlinear system. The numerical results also indicate that the amplitude of the gap soliton decreases as the nonlinear interaction strength increases, which accords well with the analytical prediction. Finally, long-time dynamical evolution for the GPE is performed by the time-splitting Fourier spectrum method to investigate the dynamical stability of gap solitons. It is shown that the on-site solitons are always dynamically stable, while the off-site solitons are always unstable. However, both stable and unstable in-phase or out-phase dipole solitons, which are not bifurcated from the Bloch band, indeed exist. For a type of out-phase soliton, there is a critical value $ q_c$ when the chemical potential μ is fixed. The solitons are linearly stable as $ q>q_c$ , while they are linearly unstable for $ q<q_c$ . Therefore, the modulus q plays an important role in the stability of gap solitons. One can change the dynamical behavior of gap solitons by adjusting the modulus of external potential in experiment. We also find that there exists a kind of gap soliton, in which the soliton is dynamically unstable if only the two-body interaction is considered, but it becomes stable when the three-body interaction is taken into account. This indicates that the three-body interaction has influence on the stability of gap solitons.
2020, 69 (1): 010302.
doi: 10.7498/aps.69.20191424
Abstract +
Soliton is an exotic topological excitation, and it widely exists in various nonlinear systems, such as nonlinear optics, Bose-Einstein condensates, classical and quantum fluids, plasma, magnetic materials, etc. A stable soliton can propagate with constant amplitude and velocity, and maintain its shape. Two-dimensional and three-dimensional solitons are usually hard to stabilize, and how to realize stable two-dimensional or three-dimensional solitons has aroused the great interest of the researchers. Ring dark soliton is a kind of two-dimensional soliton, which was first theoretically predicted and experimentally realized in nonlinear optical systems. Compared with the usual two-dimensional solitons, ring dark solitons have good stability and rich dynamical behaviors. Owing to their highly controllable capability, Bose-Einstein condensates provide a new platform for studying the ring dark solitons. Based on the recent progress in Bose-Einstein condensates and solitons, this paper reviews the research on the analytic solutions, stability, as well as the decay dynamics of ring dark solitons in Bose-Einstein condensates. A transform method is introduced, which generalizes the analytic solutions of ring dark solitons from a homogeneous system with time-independent nonlinearity to a harmonically trapped inhomogeneous system with time-dependent nonlinearity. The stability phase diagram of the ring dark soliton under deformation perturbations is discussed by numerically solving the Gross-Pitaevskii equations in the mean-field theory. A method of enhancing the stability of ring dark solitons by periodically modulating the nonlinear coefficients is introduced. It is also shown that the periodically modulated nonlinear coefficient can be experimentally realized by the Feshbach resonance technology. In addition, we discuss the dynamics of the decay of ring dark solitons. It is found that the ring dark soliton can decay into various vortex clusters composed of vortices and antivortices. This opens a new avenue to the investigation of vortex dynamics and quantum turbulence. It is also found that the ring dark solitons combined with periodic modulated nonlinearity can give rise to the pattern formation, which is an interesting nonlinear phenomenon widely explored in all the fields of nature. Finally, some possible research subjects about ring dark solitons in future research are also discussed.
2020, 69 (1): 010501.
doi: 10.7498/aps.69.20191385
Abstract +
Nonlinear waves are ubiquitous in various physical systems, and they have become one of the research hotspots in nonlinear physics. For the experimental realization, observation and application of nonlinear waves, it is very important to understand the generation mechanism, and determine the essential excitation conditions of various nonlinear waves. In this paper, we first briefly review the experimental and theoretical research progress of nonlinear waves in recent years. Based on the exact nonlinear wave solutions and linear stability analysis results, we systemically discuss how to establish the quantitative relations between fundamental nonlinear waves and modulation instability. These relations would deepen our understanding on the mechanism of nonlinear waves. To solve the excitation conditions degenerations problem for some nonlinear waves, we further introduce the perturbation energy and relative phase to determine the excitation conditions of nonlinear waves. Finally, we present a set of complete parameters that can determine the excitation conditions of nonlinear waves, and give the excitation conditions and phase diagrams of the fundamental nonlinear waves. These results can be used to realize controllable excitation of nonlinear waves, and could be extended to many other nonlinear systems.
2020, 69 (1): 010502.
doi: 10.7498/aps.69.20191384
Abstract +
In this paper, we study the generation mechanism of bright and dark solitary waves and rogue wave for the fourth-order dispersive nonlinear Schrödinger (FODNLS) equation, which can not only model the nonlinear propagation and interaction of ultrashort pulses in the high-speed optical fiber transmission system, but also govern the nonlinear spin excitations in the onedimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole-dipole interaction. Firstly, via the phase plane analysis, we obtain both the homoclinic and heteroclinic orbits for the two-dimensional plane autonomous system reduced from the FODNLS equation. Further, we derive the bright and dark solitary wave solutions under the corresponding conditions, which reveals the relationship between the homoclinic (heteroclinic) orbit and solitary wave. Secondly, based on the exact first-order breather solution of the FODNLS equation over a nonvanishing background, we give the explicit expressions of group and phase velocities, and reveal that there exists a jump in both the velocities. Finally, in order to verify that the breather becomes a rogue wave at the jumping point, we obtain the first-order rogue wave solution by taking the limit of the breather solution at such point, which confirms the relationship of the generation of rogue wave with the velocity discontinuity.
2020, 69 (1): 010503.
doi: 10.7498/aps.69.20191172
Abstract +
Multiple soliton solutions are fundamental excitations. There are many kinds of equivalent representations for multiple soliton solutions such as the Hirota forms, Wronskian and/or double Wronskian expressions and Phaffian representations. Recently, in the studies of multi-place nonlocal systems, we find that there are a type of novel but equivalent simple and elegant forms to describe multiple soliton solutions for various integrable systems. In this paper, we mainly review novel types of expressions of multiple soliton solutions for some kinds of nonlinear integrable systems. Meanwhile, some completely new expressions for the Sawada-Kortera equations, the asymmetric Nizhnik-Novikov-Veselov system, the modified KdV equation, the sine-Gordon equation, the Ablowitz-Kaup-Newell-Segue system and the completely discrete H1 equation are firstly given in this paper. New expressions usually possess explicit full reversal symmetries including parity, time reversal, soliton initial position reversal and charge conjugate reversal. These kinds of explicitly symmetric forms are very useful and convenient in the studies on the nonlinear physical problems such as the multi-place nonlocal systems and the resonant structures.
2020, 69 (1): 010504.
doi: 10.7498/aps.69.20191240
Abstract +
From a microscopic perspective, the single extreme rogue wave event can be thought of as the spatiotemporally localized rational solutions of the underlying integrable model. A typical example is the fundamental Peregrine rogue wave, who in general entails a three-fold peak amplitude, while making its peak position arbitrary on a finite continuous-wave background. This kind of bizarre wave structure agrees well with the fleeting nature of realistic rogue waves and has been confirmed experimentally, first in nonlinear fibers, then in water wave tanks and plasmas, and recently in an irregular oceanic sea state. In this review, with a brief overview of the current state of the art of the concepts, methods, and research trends related to rogue wave events, we mainly discuss the fundamental Peregrine rogue wave solutions as well as their recent progress, intended for three typical integrable models, namely, the long-wave short-wave resonant equation, the three-wave resonant interaction equation, and the nonlinear Schrödinger and Maxwell–Bloch equation. Basically, while the first two models can describe the resonant interaction among optical waves, the latter governs the interaction between the optical waves and the resonant medium. For each integrable model, we present explicitly its Lax pair, Darboux transformation formulas, and fundamental Peregrine rogue wave solutions, in a self-consistent way. We confirm by convincing examples that these fundamental rogue wave solutions exhibit universality and can be applied to the multi-component or the higher-order versions of the current integrable models. By means of numerical simulations, we demonstrate as well several novel rogue wave dynamics such as coexisting rogue waves, complementary rogue waves, and Peregrine solitons of self-induced transparency.
2020, 69 (1): 014208.
doi: 10.7498/aps.69.20191347
Abstract +
The study on soliton molecules is one of the important topics in nonlinear science especially in nonlinear optics. The bright soliton molecules have been experimentally observed in optics, however, the dark soliton molecules have not yet been experimentally observed. Theoretically, the soliton molecules have been found for some coupled nonlinear systems. Nevertheless, the soliton molecules have not been obtained for non-coupled single component nonlinear models. In this paper, we first study the exact periodic waves (soliton lattices) and solitary waves for a nonlinear nonintegrable optical model with second and third order dispersions and high order nonlinear effects including self-steeping, Raman scattering and nonlinear dispersion. Two types of dark soliton lattice and three types of soliton lattice are explicitly exhibited for general nonintegrable system. Five types of bright (with and without gray background), dark and gray solitons can be obtained from the limit cases of the modules of the soliton lattices. For an integrable case, using a novel generalized bilinear form of a single component nonlinear system, the multi-soliton solutions are obtained and expressed by a completely new form which are invariant under the full reversal transformations such as the parity, the time reversal, the charge conjugate and the field reversal. To find soliton molecules, a novel mechanism, the velocity resonant, is proposed. Starting from the multi-soliton solutions and using the velocity resonance mechanism, the analytical expression of the dark soliton molecules can be readily obtained. For the model given in this paper, the integrable higher order nonlinear Schrodinger equation, one can proved that the interactions among the dark soliton molecules and the usually solitons are elastic. It is worth pointing out that soliton molecules can also exist in the case of nonintegrable systems.
2020, 69 (1): 014701.
doi: 10.7498/aps.69.20191308
Abstract +
By the reductive perturbation method, we investigate the Rogue waves in a fluid-filled elastic tube. Based on a nonlinear Schrodinger equation obtained from a fluid-filled elastic tube, the rouge wave solution in the fluid-filled elastic tube is discussed. The characteristics of a single rouge waveare studied for this system. Then, the effects of the system parameters, such as the wave number k, the parameters $\epsilon$ , the density of the fluid, the thickness of the elastic tube, the Yang's modulus of the elastic tube, and the radius of the elastic tube on the rouge wave are also investigated. Finally, the model is applied to the blood vessels of both animal and the human to ascertain the effects of the rouge wave in different arteries and vessels. The results of the present study may have potential applications in medical science.
2020, 69 (1): 017501.
doi: 10.7498/aps.69.20191352
Abstract +
In this paper, we introduce some new excited states of magnetization in ferromagnetic nanowires, including Akhmediev breathers, Kuznetsov-Ma soliton and rogue wave in isotropic ferromagnetic nanowires, and rogue wave in anisotropic ferromagnetic nanowires driven by spin-polarized current. The isotropic case demonstrates a spatial periodic process of a magnetic soliton forming the petal with four pieces and a localized process of the spin-wave background. In a limit case, we get rogue waves and clarify its formation mechanism. In the case of anisotropy, it is found that the generation of rogue waves mainly comes from the accumulation of energy and rapid dispersion in the center. In addition, rogue waves are unstable, the spin-polarized current can control the exchange rate of magnons between the envelope soliton and the background. These results can be useful for the exploration of nonlinear excitation in Bosonic and fermionic ferromagnet.
