-
Modeling the solute transport in geological porous media is of both theoretical interest and practical importance. Of several approaches, the continuous time random walk method is a most successful one that can be used to quantitatively predict the statistical features of the process, which are ubiquitously anomalous in the case of high Péclet numbers and normal in the case of low Péclet numbers. It establishes a quantitative relation between the spatial moment of an ensemble of solute particles and the waiting time distribution in the model. However, despite its success, the classical version of this model is a " static” one in the sense that there is no tuning parameter in the waiting time distribution that can reflect the relative strength of advection and diffusion which are two mechanisms that underlie the transport process, hence it cannot be used to show the transition from anomalous to normal transport as the Péclet numbers decreases. In this work, a new continuous time random walk model is established by taking into account these two different origins of solute particle transport in a geological porous medium. In particular, solute transitions due to advection and diffusion are separately treated by using a mixture probability model for the particle’s waiting time distribution, which contains two terms representing the effects of advection and diffusion, respectively. By varying the weights of these two terms, two limiting cases can be obtained, i.e. the advection-dominated transport and the diffusion-dominated transport. The values of scaling exponent β of the mean square displacement versus time,
${\left( {\Delta {x} } \right)^2} \sim {t^{\rm{\beta }}}$ , are derived for both cases by using our model, which are consistent with previous results. In the advection dominant case with the Péclet number going to infinity, the scaling exponent β is found to be equal to$3 - {\rm{\alpha }}$ where${\rm{\alpha }} \in \left( {1,2} \right)$ is the anomaly exponent in the advection-originated part of the waiting time distribution that${{\rm{\omega }}_1}\left( {t} \right) \sim {{t}^{ - 1 - {\rm{\alpha }}}}$ . As the Péclet number decreases, the diffusion-originated part of the waiting time distribution begins to have a stronger influence on the transport process and in the limit of the Péclet number going to 0 we observe a gradual transition of β from$3 - {\rm{\alpha }}$ to 1, indicating that the underlying transport process changes from anomalous to normal transport. By incorporating advection and diffusion as two mechanisms giving rise to solute transport in the continuous time random walk model, we successfully capture the qualitative transition of the transport process as the Péclet number is varied, which is, however, elusive from the classical continuous time random walk model. Also established are the corresponding macroscopic transport equations for both anomalous and normal transport, which are consistent with previous findings as well. Our model hence fully describes the transition from normal to anomalous transport in a porous medium as the Péclet number increases in a qualitative and semi-quantitative way.-
Keywords:
- dynamical origins /
- continuous time random walk /
- anomalous transport /
- macroscopic transport equation
[1] 李娜,任理 2012 水科学进展 23 881
Li N, Ren L 2012 Adv. Water Sci. 23 881
[2] 包景东 2005 物理学进展 25 259
Bao J D 2005 Prog. Phys. 25 259
[3] Berkowitz B, Cortis A, Dentz M, Scher H 2006 Rev. Geophys. 44 RG2003
[4] Metzler R, Klafter J 2000 Phys. Rep. 339 1
Google Scholar
[5] Metzler R, Barkai E, Klafter J 1999 Phys. Rev. Lett. 82 3563
Google Scholar
[6] Ai B Q, He Y F 2010 J. Chem. Phys. 132 094504
Google Scholar
[7] Ai B Q, Shao Z G, Zhong W R 2012 J. Chem. Phys. 137 174101
Google Scholar
[8] Xu J, Jiang G 2018 Phys. Rev. E 97 052132
[9] Zhang H, Li G H 2016 Chin. Phys. B 25 110504
Google Scholar
[10] Adams E E, Gelhar L W 1992 Water Resour. Res. 28 3293
Google Scholar
[11] Levy M, Berkowitz B 2003 J. Contam. Hydrol. 64 203
Google Scholar
[12] Cortis A, Berkowitz B 2004 Soil Sci. Soc. Am. J. 68 1539
Google Scholar
[13] Bijeljic B, Mostaghimi P, Blunt M J 2011 Phys. Rev. Lett. 107 204502
Google Scholar
[14] de Anna P, Quaife B, Biros G, Juanes R 2017 Phys. Rev. Fluids 2 124103
Google Scholar
[15] Nissan A, Berkowitz B 2018 Phys. Rev. Lett. 120 054504
Google Scholar
[16] Nissan A, Berkowitz B 2019 Phys. Rev. E 99 033108
Google Scholar
[17] Yang X R, Wang Y 2019 Sci. Rep. 9 4601
Google Scholar
[18] Wang Y 2013 Phys. Rev. E 87 032144
Google Scholar
[19] Reis F D A A, di Caprio D 2014 Phys. Rev. E 89 062126
Google Scholar
[20] Liu J, Zhu Y, He P, Chen X, Bao J D 2017 Eur. Phys. J. B 90 70
Google Scholar
[21] Wang Y, Yang X R 2015 Chin. Phys. B 24 118902
Google Scholar
-
图 1 拉萨周边地区某岩心样本的CT扫描图像(左)及其对应的孔隙空间(右)
Figure 1. Left: Micro-CT image of a rock sample from Lhasa; Right: the corresponding pore space extracted from the left image.
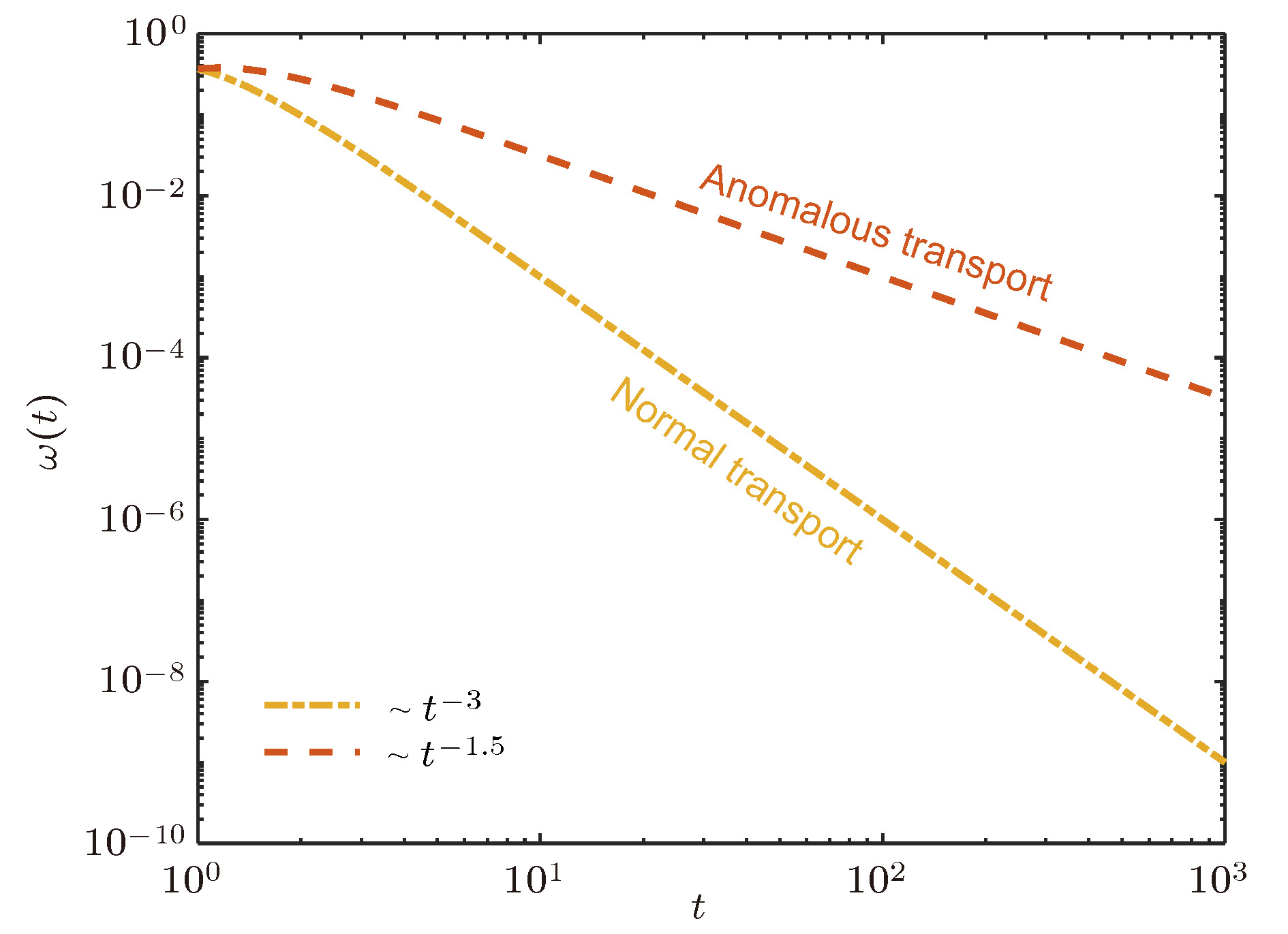
图 2 等待时间分布ω(t)~t–1–α示意图, 不同统计特征导致定性上不同的输运行为. 以α = 2为界, 当α > 2时输运行为是正常的, 当0 < α < 2时为反常.本文尤其关注1 < α < 2的情况
Figure 2. Schematic of the waiting time distribution ω(t)~t–1–α. The value of α qualitatively determines the transport dynamics. When α > 2, the transport behavior is normal; while when 0 < α < 2, anomalous transport appears. In this work, we focus on the case 1 < α < 2.
-
[1] 李娜,任理 2012 水科学进展 23 881
Li N, Ren L 2012 Adv. Water Sci. 23 881
[2] 包景东 2005 物理学进展 25 259
Bao J D 2005 Prog. Phys. 25 259
[3] Berkowitz B, Cortis A, Dentz M, Scher H 2006 Rev. Geophys. 44 RG2003
[4] Metzler R, Klafter J 2000 Phys. Rep. 339 1
Google Scholar
[5] Metzler R, Barkai E, Klafter J 1999 Phys. Rev. Lett. 82 3563
Google Scholar
[6] Ai B Q, He Y F 2010 J. Chem. Phys. 132 094504
Google Scholar
[7] Ai B Q, Shao Z G, Zhong W R 2012 J. Chem. Phys. 137 174101
Google Scholar
[8] Xu J, Jiang G 2018 Phys. Rev. E 97 052132
[9] Zhang H, Li G H 2016 Chin. Phys. B 25 110504
Google Scholar
[10] Adams E E, Gelhar L W 1992 Water Resour. Res. 28 3293
Google Scholar
[11] Levy M, Berkowitz B 2003 J. Contam. Hydrol. 64 203
Google Scholar
[12] Cortis A, Berkowitz B 2004 Soil Sci. Soc. Am. J. 68 1539
Google Scholar
[13] Bijeljic B, Mostaghimi P, Blunt M J 2011 Phys. Rev. Lett. 107 204502
Google Scholar
[14] de Anna P, Quaife B, Biros G, Juanes R 2017 Phys. Rev. Fluids 2 124103
Google Scholar
[15] Nissan A, Berkowitz B 2018 Phys. Rev. Lett. 120 054504
Google Scholar
[16] Nissan A, Berkowitz B 2019 Phys. Rev. E 99 033108
Google Scholar
[17] Yang X R, Wang Y 2019 Sci. Rep. 9 4601
Google Scholar
[18] Wang Y 2013 Phys. Rev. E 87 032144
Google Scholar
[19] Reis F D A A, di Caprio D 2014 Phys. Rev. E 89 062126
Google Scholar
[20] Liu J, Zhu Y, He P, Chen X, Bao J D 2017 Eur. Phys. J. B 90 70
Google Scholar
[21] Wang Y, Yang X R 2015 Chin. Phys. B 24 118902
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6482
- PDF Downloads: 53
- Cited By: 0
