-
Understanding the statistical fluctuations of lattice observables over the gauge configurations is important both theoretically and practically. It provides a physical insight into tackling the famous signal-to-noise problem and the sign problem, and inspires new thoughts in developing methods to improve the signal of lattice calculations. Among many efforts, exploring the relationship between the real part and imaginary part of lattice numerical result is a new method to understand lattice signal and error, because both the real part and imaginary part come from the same sample of gauge field and their distributions on the gauge sample are related in principle. Specifically, by analyzing the distributions of the real part and imaginary part of quenched lattice two-point function with high statistics and non-zero momentum, this work proposes a possible quantitative formula connecting these two distributions as
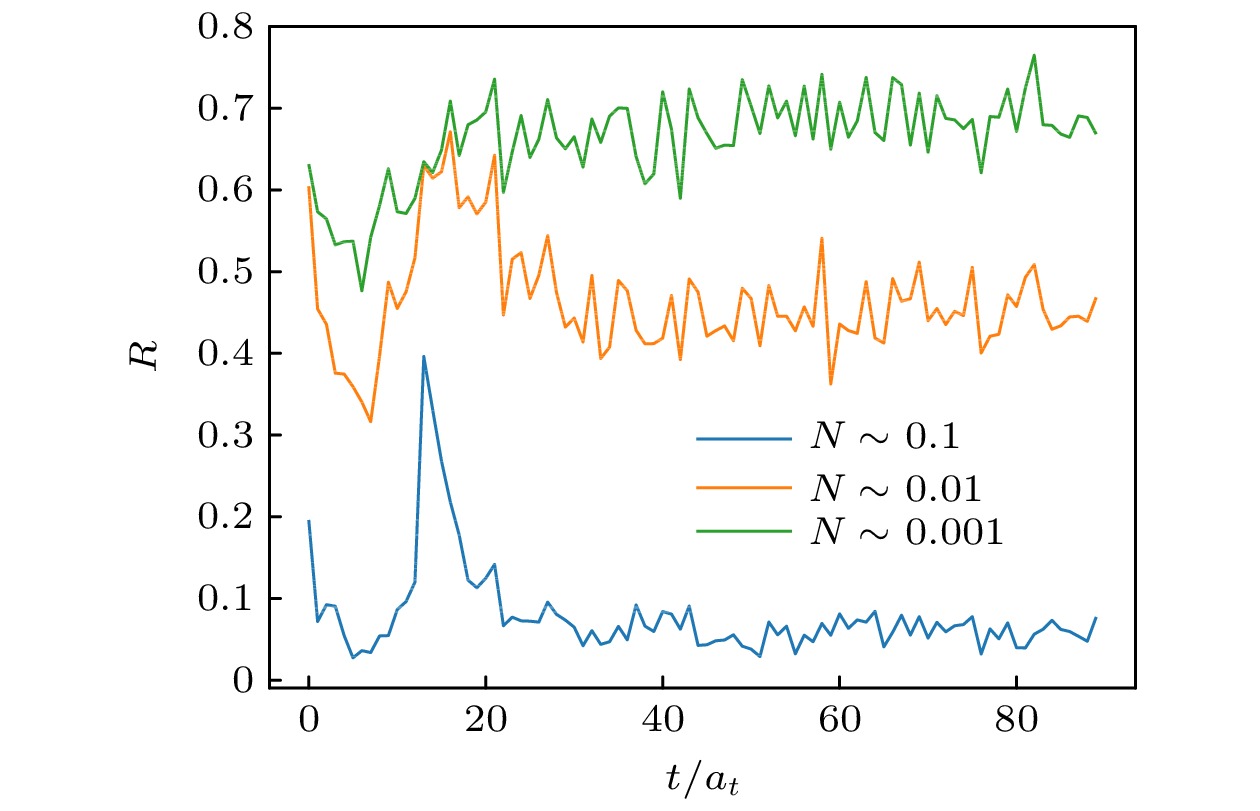
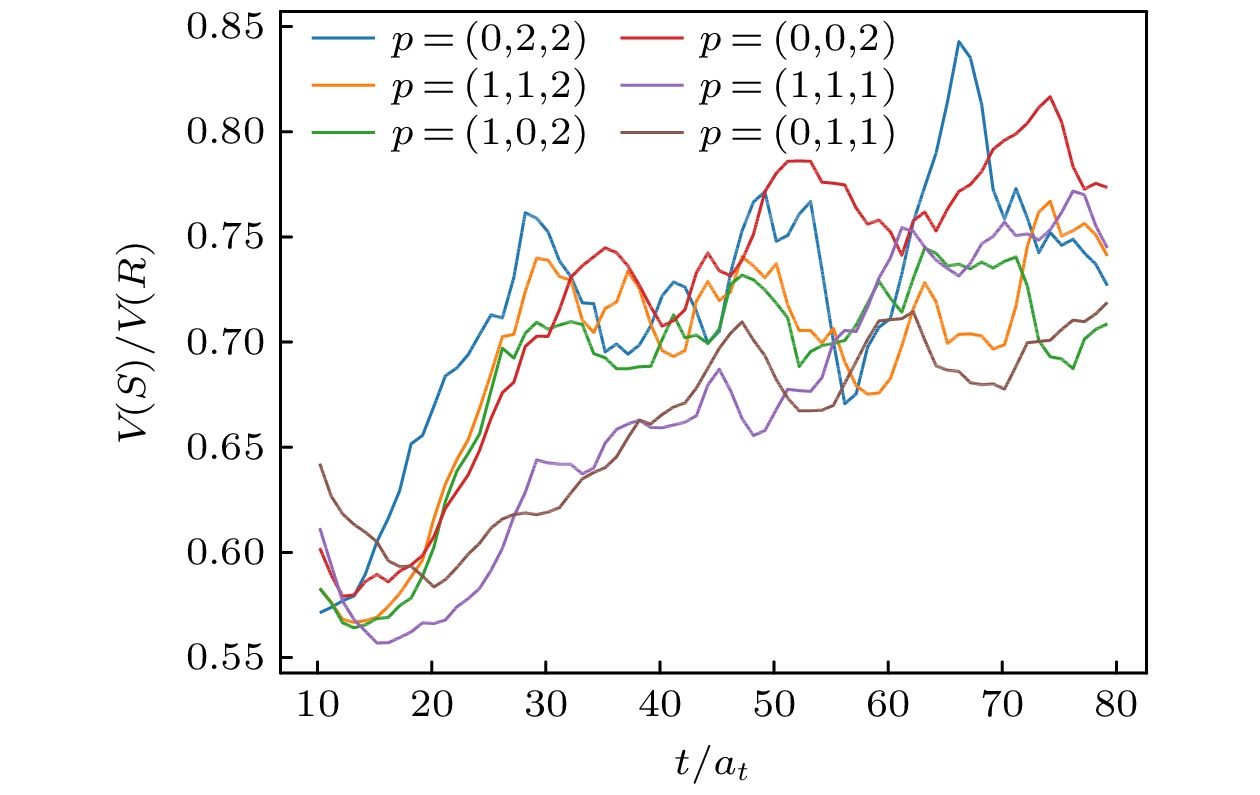
$R(x)=\displaystyle\int {\rm{d}}y S(y-x) \left[I(y) K(U_y)\right]$ , where$R(x)$ denotes the real-part distribution,$I(x)$ the imaginary-part distribution,$S(x)$ the underlying signal distribution and$K(U_x)$ a kernel function of the gauge field. This theoretical assumption has universal validity because the kernel function contains the gauge field information that determines all the distributions. The formula is numerically verified by calculating the non-trivial statistical correlations of the real part and the kernel-function-modified imaginary part under the further assumption of the kernel function. It is found that the most naïve guess of$K(U_x)=1$ does not work, which leads to no statistically significant correlation. Meanwhile, the assumption that$K(U_x)$ is only a sign function works well, giving rise to$\sim70\%$ correlation. Then, through the process of adding random distortions to the absolute values of the imaginary part, it is found that even a slight distortion, of around 1% could result in a significant reduction in the correlation between the real part and imaginary part down to less than 50% or lower. This essentially proves that the observed$\sim70\%$ correlation is highly non-trivial and the hypothesis that$K(U_x)$ is a sign function captures at least some of the physical mechanisms behind the scenes. Employing this correlation, the variance of lattice results can be improved by around 40%. It is not a significant improvement in practice; however, this study offers an innovative strategy to understand the source of statistical uncertainties in lattice QCD and to improve the signal-to-noise ratio in lattice calculation. Further research on the ability to use machine learning on various more accurate lattice data will hopefully give better instructions and constraint on the form of the kernel function.-
Keywords:
- lattice quantum chromodynamics /
- sampling distribution /
- sum of probability distributions /
- signal-to-noise ratio
[1] 陈莹, 丁亨通, 冯旭, 等 2020 现代物理知识 32 36
Chen Y, Ding H T, Feng X, et al. 2020 Modern Physics 32 36
[2] Chang C C, Nicholson A N, Rinaldi E, et al. 2018 Nature 558 91
Google Scholar
[3] Borsanyi Sz, Fodor Z, Guenther J N, et al. 2021 Nature 593 51
Google Scholar
[4] Yang Y B, Liang J, Bi Y J, et al. 2018 Phys. Rev. Lett. 121 212001
Google Scholar
[5] Joó Bálint, Jung C, Christ N H, et al. 2019 Eur. Phys. J. A 55 199
Google Scholar
[6] Liu K F, Liang J, Yang Y B 2018 Phys. Rev. D 97 034507
Google Scholar
[7] Liang J, Alexandru A, Draper T, et al. 2023 arXiv: 2301.04331 [hep-lat]
[8] Liang J, Yang Y B, Draper T, et al. 2018 Phys. Rev. D 98 074505
Google Scholar
[9] Yang Y B, Gong M, Liang J, et al. 2018 Phys. Rev. D 98 074506
Google Scholar
[10] Endres M G, Kaplan D B, Lee J W, et al. 2011 Phys. Rev. Lett. 197 201601
[11] Gupta R 1997 arXiv: hep-lat/9807028[hep-lat]
[12] DeGrand T 2012 Phys. Rev. D 86 014512
[13] Wagman M L, Savage M J 2017 arXiv: 1704.07356[hep-lat]
[14] Wagman M L 2017 arXiv: 1711.00062[hep-lat]
[15] Sheikholeslami B, Wohlert R 1985 Nucl. Phys. B 259 572
Google Scholar
[16] Gui L C, Dong J M, Chen Y, et al. 2019 Phys. Rev. D 100 054511
[17] Parisi G 1984 Phys. Rep. 103 203
Google Scholar
[18] Lepage G P 1989 Proceedings of Theoretical Advanced Study Institute in Elementary Particle Physics (TASI89) Boulder, Colorado, United States, June 5–30, 1989 p97
[19] Burnier Y, Rothkopf A 2013 Phys. Rev. Lett. 111 182003
Google Scholar
[20] Hansen M, Lupo A, Tantalo N 2019 Phys. Rev. D 99 094508
[21] Chen S Y, Ding H T, Liu F Y, et al. 2021 arXiv: 2110.13521 [hep-lat]
-
图 1 纵坐标为对数坐标情况下, 不同量子数和不同动量的两点关联函数
Figure 1. Two-point correlations function with different quantum numbers and momenta when the vertical axis is in log scale
图 2 $ p^2=1 $的赝标两点函数其实部(上半部分)虚部(下半部分)在规范组态上的分布, 从左至右分别对应$ t/a_t=1 $, 30和90的情况
Figure 2. The real-part (upper panel) and imaginary-part (lower panel) distributions of the pseudoscalar two-point functions with $ p^2=1 $ over gauge configurations. From left to right, the figures are for $ t/a_t=1 $, 30 and 90, respectively.
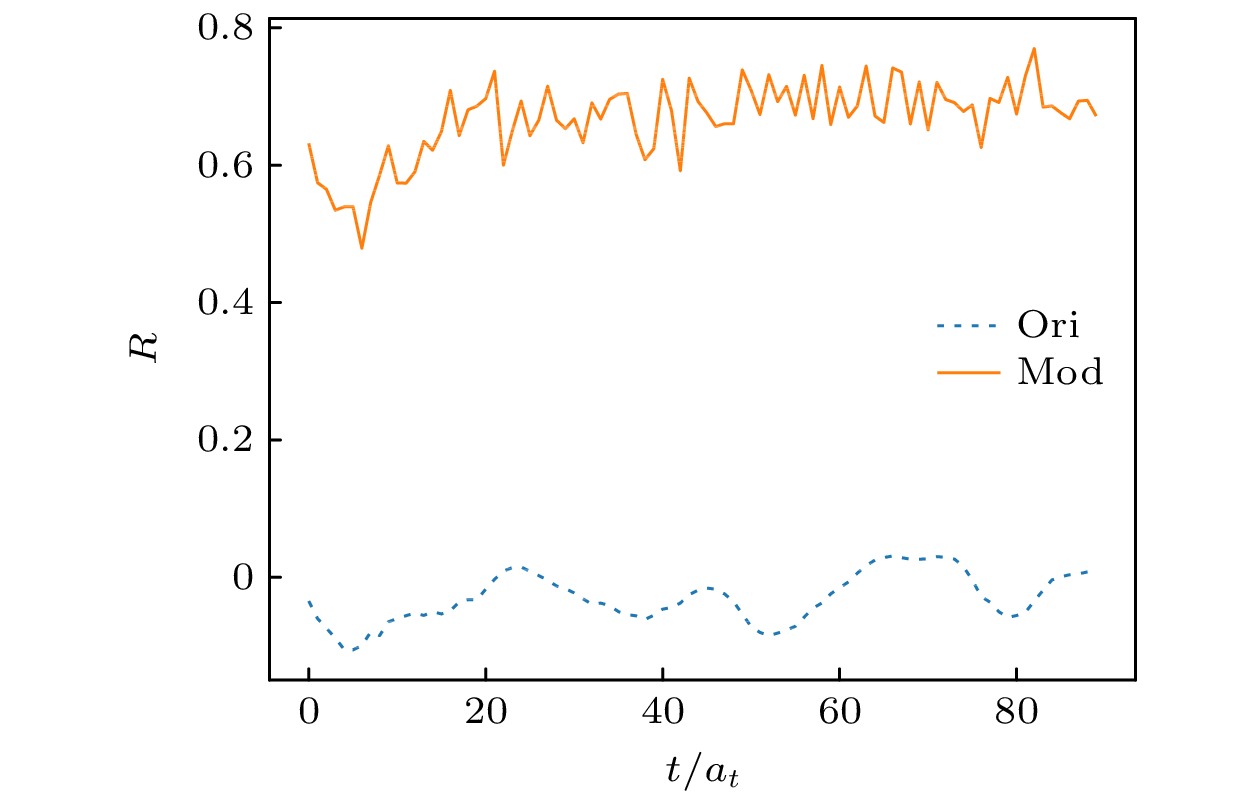
图 3 赝标单位动量两点关联函数实部与虚部的统计相关性. 蓝色虚线表示原始数据, 橙色实线表示符号修正过的数据
Figure 3. Statistical correlations between the real and imaginary parts of the pseudoscalar two-point correlation function with unit momentum, where the blue dashed line represents the original data, and the orange solid one is for the data after sign-correction.
图 4 在修正符号的基础上, 考虑对虚部的值进行扰动后的赝标单位动量两点关联函数实部与虚部的统计相关性
Figure 4. On the basis of sign-correction, the statistical correlations between the real and imaginary parts of the pseudoscalar two-point correlation function with unit momentum after distortions on the absolute values of the imaginary parts.
图 5 不同量子数两点关联函数的方差改进
Figure 5. The variance improvements of two-point correlation functions with different quantum numbers.
图 6 不同动量矢量两点关联函数的方差改进
Figure 6. The variance improvements of two-point correlation functions with different momenta.
-
[1] 陈莹, 丁亨通, 冯旭, 等 2020 现代物理知识 32 36
Chen Y, Ding H T, Feng X, et al. 2020 Modern Physics 32 36
[2] Chang C C, Nicholson A N, Rinaldi E, et al. 2018 Nature 558 91
Google Scholar
[3] Borsanyi Sz, Fodor Z, Guenther J N, et al. 2021 Nature 593 51
Google Scholar
[4] Yang Y B, Liang J, Bi Y J, et al. 2018 Phys. Rev. Lett. 121 212001
Google Scholar
[5] Joó Bálint, Jung C, Christ N H, et al. 2019 Eur. Phys. J. A 55 199
Google Scholar
[6] Liu K F, Liang J, Yang Y B 2018 Phys. Rev. D 97 034507
Google Scholar
[7] Liang J, Alexandru A, Draper T, et al. 2023 arXiv: 2301.04331 [hep-lat]
[8] Liang J, Yang Y B, Draper T, et al. 2018 Phys. Rev. D 98 074505
Google Scholar
[9] Yang Y B, Gong M, Liang J, et al. 2018 Phys. Rev. D 98 074506
Google Scholar
[10] Endres M G, Kaplan D B, Lee J W, et al. 2011 Phys. Rev. Lett. 197 201601
[11] Gupta R 1997 arXiv: hep-lat/9807028[hep-lat]
[12] DeGrand T 2012 Phys. Rev. D 86 014512
[13] Wagman M L, Savage M J 2017 arXiv: 1704.07356[hep-lat]
[14] Wagman M L 2017 arXiv: 1711.00062[hep-lat]
[15] Sheikholeslami B, Wohlert R 1985 Nucl. Phys. B 259 572
Google Scholar
[16] Gui L C, Dong J M, Chen Y, et al. 2019 Phys. Rev. D 100 054511
[17] Parisi G 1984 Phys. Rep. 103 203
Google Scholar
[18] Lepage G P 1989 Proceedings of Theoretical Advanced Study Institute in Elementary Particle Physics (TASI89) Boulder, Colorado, United States, June 5–30, 1989 p97
[19] Burnier Y, Rothkopf A 2013 Phys. Rev. Lett. 111 182003
Google Scholar
[20] Hansen M, Lupo A, Tantalo N 2019 Phys. Rev. D 99 094508
[21] Chen S Y, Ding H T, Liu F Y, et al. 2021 arXiv: 2110.13521 [hep-lat]
DownLoad:
Catalog
Metrics
- Abstract views: 3411
- PDF Downloads: 65
- Cited By: 0
