-
Lattice quantum chromodynamics (lattice QCD) is a theory based on quantum chromodynamics, which is widely used in strong interaction related calculations. As a research method that can give accurate and reliable theoretical results, with the improvement of computer ability, Lattice QCD is playing an increasingly important role in recent years. Distillation method is an important numerical method to calculate hadron correlation function in lattice QCD, and can improve the signal-to-noise ratio of calculated physical quantities. Distillation is a method to approximately compute full propagator via replace the laplacian operator with it's outerproduct of laplace eigenvectors. In this way, the construction of operators is independent of the inversion of propagator which is costful. The eigenvector system and perambulator can be used in different physical projects and we don't need to compute these data repeatedly. It's also convinent for computing disconnected part of correlation function. However, it also faces to the problem of large amount of data in constructing correlation function because the difficulty of compuation is proportional to the cubic of the number of eigenvectors, so it is necessary to further improve its computational efficiency. A program is developed in this work to construct correlation function of quark bilinear with distillation method, and solved the bottleneck of computing performance by using MPI(Message Passing Interface, https://www.open-mpi.org), OpenMP(Open Multi-Processing) and SIMD(Single Instruction Multiple Data) multi-level optimization technology. And this program distribute timeslices to different MPI processes because the computation of each timeslice is independent. In order to show the efficiency of our program some tests result are presented. After various tests of the program, it shows that our design can support large-scale computation. Under the strong scalability test, the parallel computing efficiency of 512 processes can still achieve about 70%. The ability of calculating correlation function is greatly improved. The correction of results also has been checked via compute pseudo-scalar correlators of charmonium. Three different
$ 0^{-+}$ operators were adopted for variational analysis and there effecitive mass plateau were compared with the effective mass obtained from the tradional method with point source. The results of distillation method are consistent with traditional method. After variational analysis, three state is obtained, which means the variational analysis take effects and the correlation functions obtained from distillation method is reasonable.-
Keywords:
- lattice quantum chromodynamics /
- distillation algorithm /
- correlation function /
- parallel computing
[1] Flynn J M, Mescia F, Tariq A S B 2003 JHEP 07 066
Google Scholar
[2] Lozano J, Agadjanov A, Gegelia J, Meißner U G, Rusetsky A 2021 Phys. Rev. D 103 034507
Google Scholar
[3] Chen C, Fischer C S, Roberts C D, Segovia J 2021 Phys. Lett. B 815 136150
Google Scholar
[4] Meißner U G 2014 Nucl. Phys. News. 24 11
Google Scholar
[5] Lähde T A, Meißner U G 2019 Lect. Notes Phys. 957 1
Google Scholar
[6] Wilson K G 1974 Phys. Rev. D 10 2445
Google Scholar
[7] Gasser J, Leutwyler H 1984 Annals Phys. 158 142
Google Scholar
[8] Diakonov D, Petrov V, Pobylitsa P, Polyakov M V, Weiss C 1996 Nucl. Phys. B 480 341
Google Scholar
[9] Rothe H J 2012 World Sci. Lect. Notes Phys. 82
[10] Brower R, Christ N, DeTar C, Edwards R, Mackenzie P 2018 EPJ Web Conf. 175 09010
Google Scholar
[11] Zhang Z, Luan Z, Xu C, Gong M, Xu S 2018 2018 IEEE Intl Conf on Parallel Distributed Processing with Applications, Ubiquitous Computing Communications, Big Data Cloud Computing, Social Computing Networking, Sustainable Computing Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom),Melbourne, VIC, Australia 605
[12] Gattringer C, Lang C B 2010 Lect. Notes Phys. 788 1
[13] Barrett R, Berry M, Chan T F, Demmel J, Donato J M, Dongarra J, Eijkhout V, Pozo R, Romine C, Vorst H V 1994 SIAM, Philadelphia 139, 140, 141
[14] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 1999 (Cambridge: Cambridge University Press) p139
[15] Wilcox W, Darnell D, Morgan R, Lewis R 2006 PoS LAT 2005 039
Google Scholar
[16] Peardon M, Bulava J, Foley J, Morningstar C, Dudek J, Edwards R G, Joó B, Lin H W, Richards D G, Juge K J 2009 Phys. Rev. D 80 054506
Google Scholar
[17] Egerer C, Edwards R G, Orginos K, Richards D G 2021 Phys. Rev. D 103 034502
Google Scholar
[18] Güsken S, Löw U, Mütter K H, Sommer R 1989 Phys. Lett. B 227 266
Google Scholar
[19] Best C, et al. 1997 Phys. Rev. D 56 2743
Google Scholar
[20] Basak S, Edwards R G, Fleming G T, Heller U M, Morningstar C, Richards D, Sato I, Wallace S 2005 Phys. Rev. D 72 094506
Google Scholar
[21] Ehmann C, Bali G 2007 PoS LATTICE 2007 094
Google Scholar
-
图 1 利用蒸馏算法计算关联函数的流程
Figure 1. The procedure of computing correlators via distillation method.
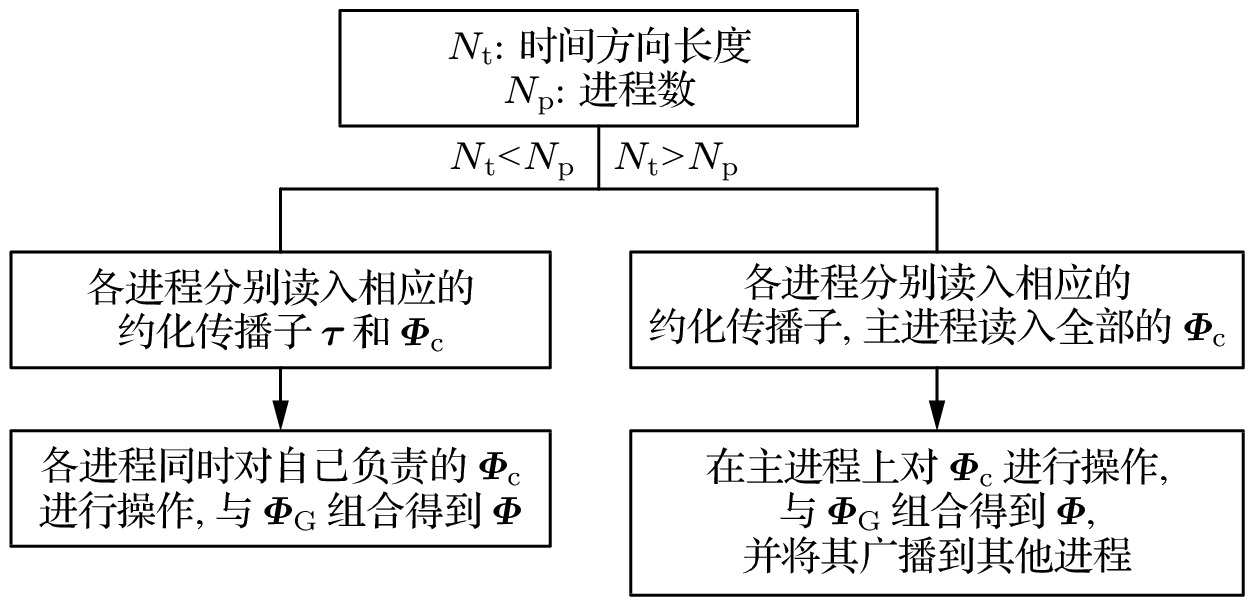
图 2 含计算约化的关联函数计算的流程. 其中
${\boldsymbol T}^A$ 和${\boldsymbol T}^B$ 表示两个中间计算量. 利用中间量的计算减少了总体的计算量, 让计算量从$\propto N_{\rm op}^2\times N_{\rm v}^4$ 变成$\propto N_{\rm op}\times N_{\rm v}^3$ , 极大地减少了计算量Figure 2. The flowchart of computing correlation function.
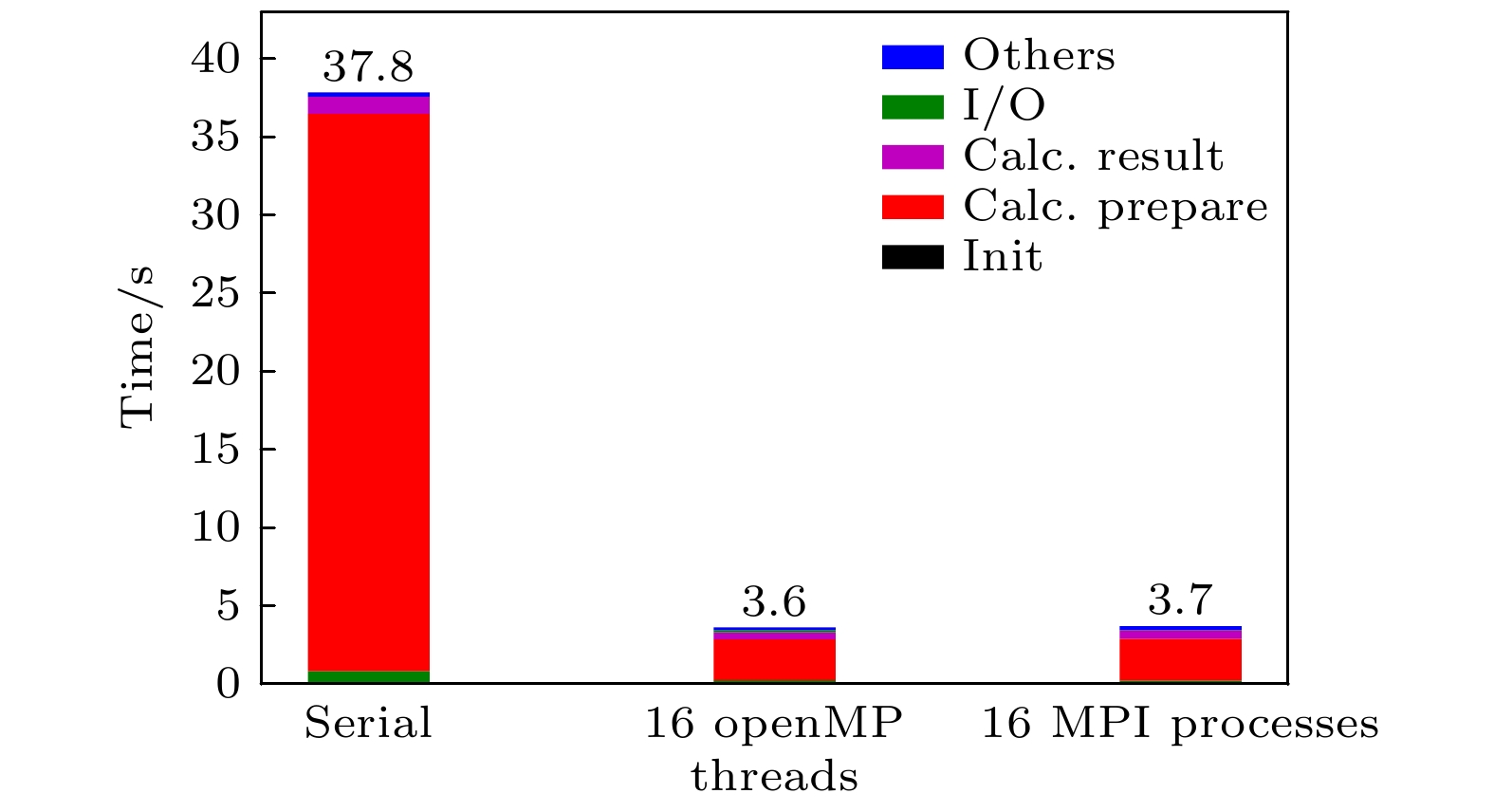
${\boldsymbol T}^A$ and${\boldsymbol T}^B$ are two intermidiate quantities. After introducted intermediate quantities, the computation consumption is highly reducted to$\propto N_{\rm op}\times N_{\rm v}^3$ .
图 3 按照时间切分实现并行计算的方式, 根据
$N_{\rm p}$ 与$N_{\rm t}$ 的相对大小, 由于数据的特性, 对τ和Φ按情况采用不同的切分方法.Figure 3. Data sgemented according to time. Two conditions are considered which decided how τ and Φ are treated because of the feature of data.
图 4 使用SIMD优化前后各阶段耗时对比. I/O代表图1中第一步和第二步的时间, Calc.prepare代表图1中第三步的时间, Calc.result代表图1中第四步的时间, Others代表图1中第五步的时间, Init代表程序初始化的时间. 图例SIMD表示启用了AVX形式的SIMD计算性能, 而Complex表示程序直接调用标准库中的复数计算函数(此处未使用SIMD计算). 其中16个MPI进程并行计算的结果是在超线程计算状态下获得
Figure 4. The cost of time of program's each part to see the effects of SIMD. I/O labels the time of first step and second step in Fig. 1, Calc.prepare labels the time of the third step in Fig. 1, Calc.result labels the time of the fourth step in Fig. 1, Others labels the time of the fifth step in Fig. 1. Init labels the time of initialization. SIMD in the picture means SIMD optimization was adopted and Complex in the picture means the stdandard library of complex computation was used. And hyper-threading technology was used for 16 MPI process.
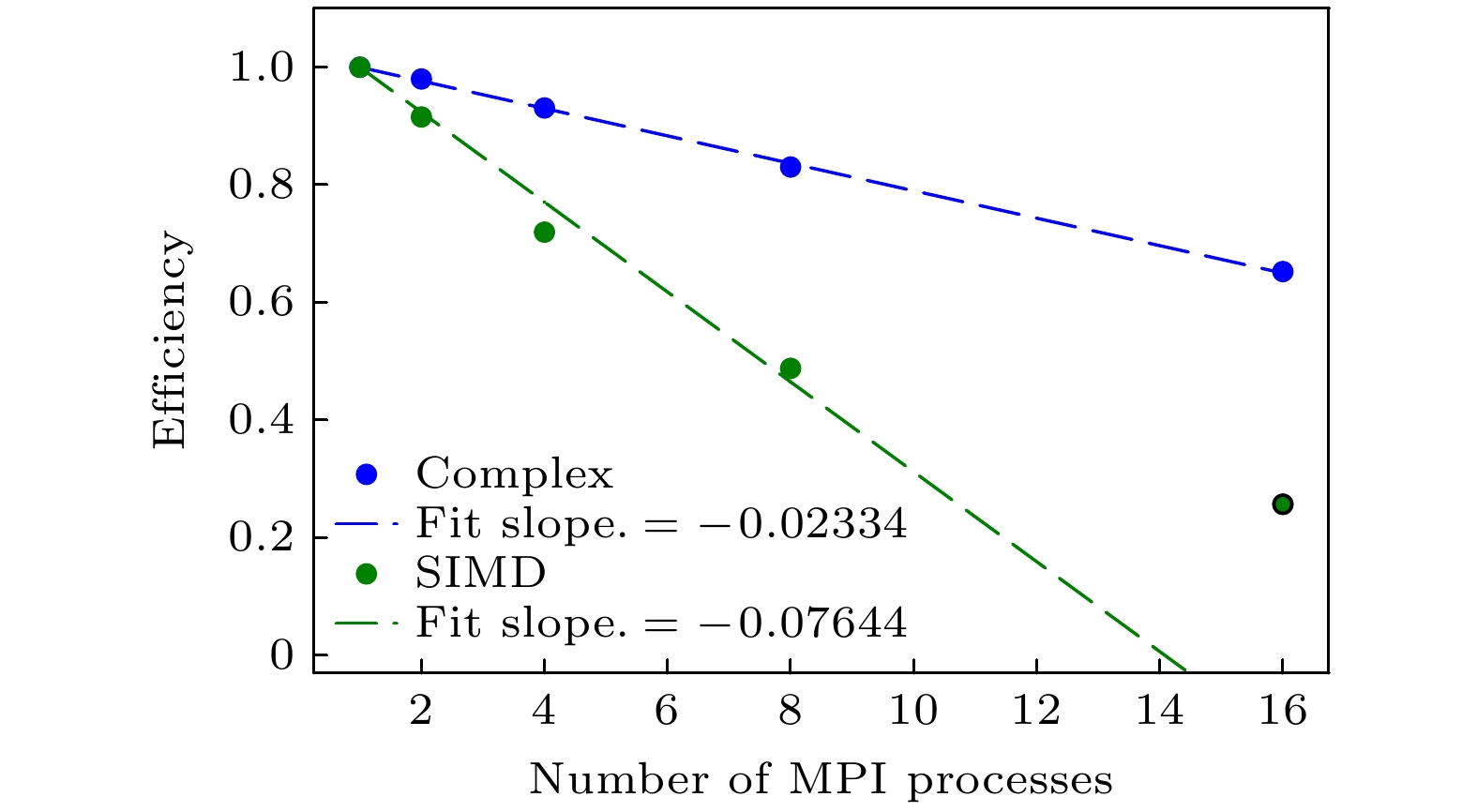
图 5 使用SIMD优化前后性能对比. 图例SIMD表示启用了AVX形式的SIMD计算性能, 而Complex表示程序直接调用标准库中的复数计算函数(此处未使用SIMD计算). 其中, 在SIMD启用时16个超线程计算结果未参与数据拟合
Figure 5. The cost of time of program's each part to see the effects of SIMD. SIMD in the picture means SIMD optimization was adopted and Complex in the picture means the stdandard library of complex computation was used. And hyper-threading technology was used for 16 MPI process.
图 6 使用OpenMP优化前后耗时对比. 图例如图4. 图例Serial表示串行版本, 即未开启OpenMP多线程和MPI多进程
Figure 6. The effects of OpenMP optimization was showed. Legends are the same as 4. Serial lables the results of serial program which means no OpenMP and MPI was adopted.
图 8 MPI并行强扩展性测试，不同MPI进程数的测试相对于16个进程的计算效率
Figure 8. MPI parallelism in strong scale tests. The efficiency of strong scale tests compared with 16 MPI processes.
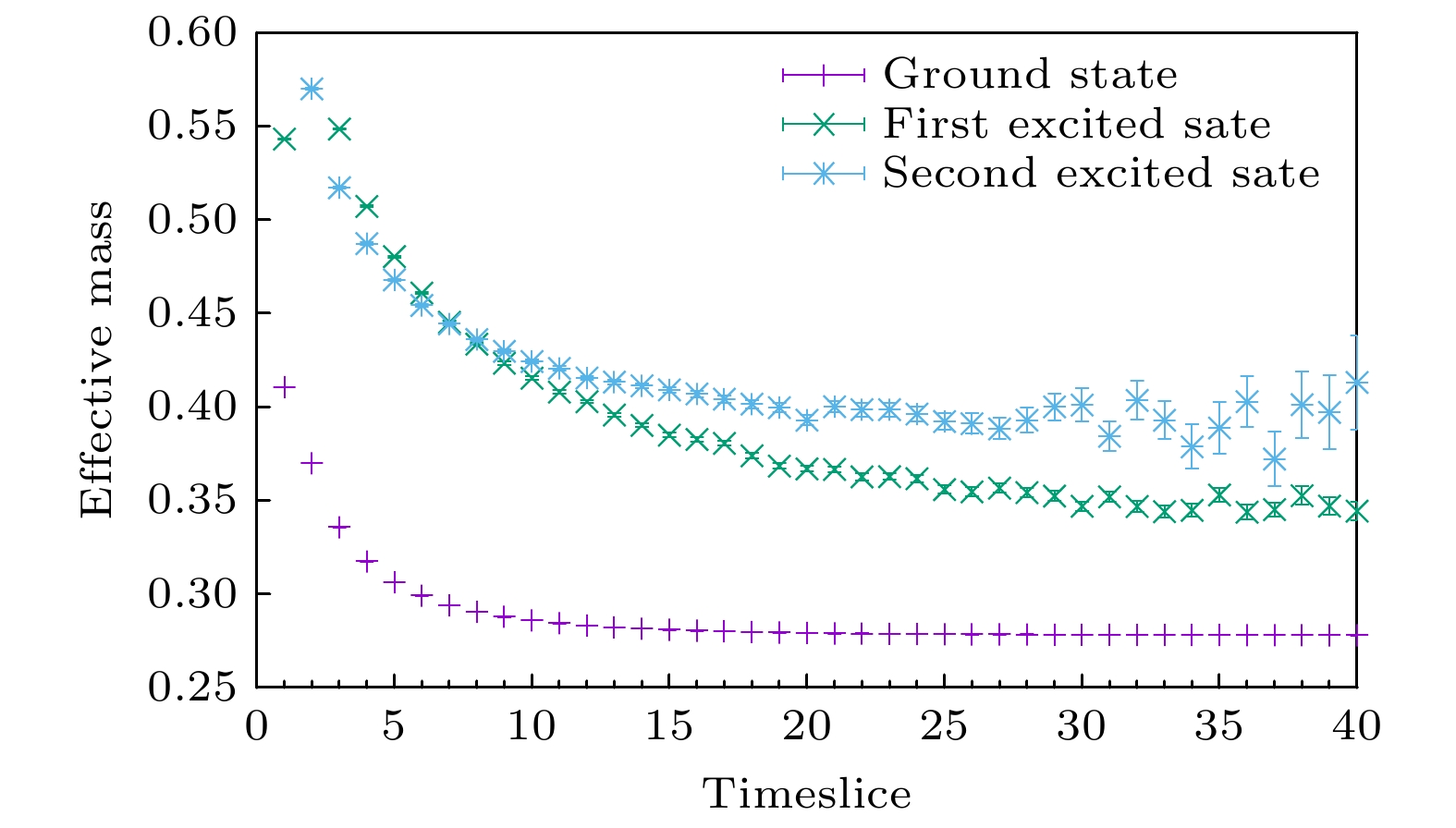
图 10 做变分前的结果. 在时间比较小时, 三个算符得到的有效质量的行为有很大差别, 证明在不同态的投影是不同的, 意味着变分会有一定的效果. 在时间较大时, 三个算符的有效质量趋于同一平台, 说明它们的量子数是相同的, 可以用来变分. traditional method表示第一个算符通过传统方法所得到的有效质量, 作为蒸馏算法的参照
Figure 10. Results before variation. The behaviors of the effective mass of these three operators are very different and it means variational analysis would give good results. When time is large enough, these three operators approach to the same plateau so that they should have the same quantum numbers. traditial method label the effective mass of first operator throgh traditional mehtod, which can is matched with distillation method.
图 11 做变分后的结果
Figure 11. Results after variation.
-
[1] Flynn J M, Mescia F, Tariq A S B 2003 JHEP 07 066
Google Scholar
[2] Lozano J, Agadjanov A, Gegelia J, Meißner U G, Rusetsky A 2021 Phys. Rev. D 103 034507
Google Scholar
[3] Chen C, Fischer C S, Roberts C D, Segovia J 2021 Phys. Lett. B 815 136150
Google Scholar
[4] Meißner U G 2014 Nucl. Phys. News. 24 11
Google Scholar
[5] Lähde T A, Meißner U G 2019 Lect. Notes Phys. 957 1
Google Scholar
[6] Wilson K G 1974 Phys. Rev. D 10 2445
Google Scholar
[7] Gasser J, Leutwyler H 1984 Annals Phys. 158 142
Google Scholar
[8] Diakonov D, Petrov V, Pobylitsa P, Polyakov M V, Weiss C 1996 Nucl. Phys. B 480 341
Google Scholar
[9] Rothe H J 2012 World Sci. Lect. Notes Phys. 82
[10] Brower R, Christ N, DeTar C, Edwards R, Mackenzie P 2018 EPJ Web Conf. 175 09010
Google Scholar
[11] Zhang Z, Luan Z, Xu C, Gong M, Xu S 2018 2018 IEEE Intl Conf on Parallel Distributed Processing with Applications, Ubiquitous Computing Communications, Big Data Cloud Computing, Social Computing Networking, Sustainable Computing Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom),Melbourne, VIC, Australia 605
[12] Gattringer C, Lang C B 2010 Lect. Notes Phys. 788 1
[13] Barrett R, Berry M, Chan T F, Demmel J, Donato J M, Dongarra J, Eijkhout V, Pozo R, Romine C, Vorst H V 1994 SIAM, Philadelphia 139, 140, 141
[14] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 1999 (Cambridge: Cambridge University Press) p139
[15] Wilcox W, Darnell D, Morgan R, Lewis R 2006 PoS LAT 2005 039
Google Scholar
[16] Peardon M, Bulava J, Foley J, Morningstar C, Dudek J, Edwards R G, Joó B, Lin H W, Richards D G, Juge K J 2009 Phys. Rev. D 80 054506
Google Scholar
[17] Egerer C, Edwards R G, Orginos K, Richards D G 2021 Phys. Rev. D 103 034502
Google Scholar
[18] Güsken S, Löw U, Mütter K H, Sommer R 1989 Phys. Lett. B 227 266
Google Scholar
[19] Best C, et al. 1997 Phys. Rev. D 56 2743
Google Scholar
[20] Basak S, Edwards R G, Fleming G T, Heller U M, Morningstar C, Richards D, Sato I, Wallace S 2005 Phys. Rev. D 72 094506
Google Scholar
[21] Ehmann C, Bali G 2007 PoS LATTICE 2007 094
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5704
- PDF Downloads: 106
- Cited By: 0
