-
Efficiently identifying multiple influential nodes is crucial for maximizing information diffusion and minimizing rumor spread in complex networks. Selecting multiple influential seed nodes requires to take into consider both their individual influence potential and their spatial dispersion within the network topology to avoid overlapping propagation ranges (“rich-club effect”). Traditional VoteRank method has two key limitations: 1) the voting contributions from a node is assumed to be consistent to all its neighbors, and the influence of topological similarity (structural homophily) on the voting preferences observed in real-world scenarios is neglected, and 2) a homogeneous voting attenuation strategy is used, which is insufficient to suppress propagation range overlap between selected seed nodes. To address these shortcomings, IMVoteRank, an improved VoteRank algorithm featuring dual innovations, is proposed in this work. First, a structural similarity-driven voting contribution mechanism is introduced. By recognizing that voters (nodes) are more likely to support candidates (neighbors) with stronger topological relationships with them, the voting contribution of neighbors is decomposed into two parts: direct connection contribution and a structural similarity contribution (quantified using common neighbors). A dynamic weight parameter θ, adjusted based on the candidate node’s degree, balances these components, significantly refining vote allocation accuracy. Second, we devise a dynamic group isolation trategy. In each iteration, after selecting the highest-scoring seed node vmax, a tightly-knit group (OG) centered around it is identified and isolated. This involves: 1) forming an initial group based on neighbor density shared with vmax, 2) expanding it by merging nodes with more connections inside the group than outside, and 3) isolating this group by setting the voting capacity (Va) of all its members to zero and virtually removing their connections from the adjacency matrix. Neighbors of vmax not in OG have their Va values reduced by half. This strategy actively forces spatial dispersion among seeds. Extensive simulations using the susceptible-infected-recovered (SIR) propagation model on nine different real-world networks (ECON-WM3, Facebook-SZ, USAir, Celegans, ASOIAF, Dnc-corecipient, ERIS1176, DNC-emails, Facebook-combined) demonstrate the superior performance of IMVoteRank. Compared with seven benchmark methods (Degree, k-shell, VoteRank, NCVoteRank, VoteRank++, AIGCrank, EWV), IMVoteRank consistently achieves significantly larger final propagation coverage (infected scale) for a given number of seed nodes and transmission probability (β = 0.1). Furthermore, seeds selected by IMVoteRank exhibit a consistently larger average shortest path length (Ls) in most networks, which proves their effective topological dispersion. This combination of high personal influence potential (optimized voting) and low redundancy (group isolation) directly translates to more effective global information dissemination, as evidenced by the SIR results. Tests on LFR benchmark networks further validate these advantages, particularly at transmission rates above the epidemic threshold. IMVoteRank effectively overcomes the limitations of traditional voting models by integrating structural similarity into the voting process and employing dynamic group isolation to ensure seed dispersion. It provides a highly effective and physically reliable method for identifying multiple influential nodes in complex networks and optimizing the trade-off between influence strength and spatial coverage. Future work will focus on improving the computational efficiency of large-scale networks and exploring the influence of meso-scale community structures.
-
Keywords:
- complex network /
- multiple influential nodes /
- voting model /
- isolation strategy
[1] Watts D J, Strogatz S H 1998 Nature 393 440
 Google Scholar
Google Scholar
[2] Barabasi A L, Albert R 1999 Science 286 509
 Google Scholar
Google Scholar
[3] Liu Y Y, Slotine J J, Barabasi A L 2011 Nature 473 167
 Google Scholar
Google Scholar
[4] Yang Z, Li Y, Liu J 2021 Proceedings of the 15th EAI International Conference on Communications and Networking (ChinaCom 2020) Shanghai, China, November 20–21, 2020 p766
[5] Li Y G, Xiao Z L, Gao A, Wu W N, Pei E R 2025 Knowl-Based Syst. 317 113434
 Google Scholar
Google Scholar
[6] Lin Y G, Wang X M, Hao F, Jiang Y C, Wu Y L, Min G Y, He D J, Zhu S C, Zhao W 2019 IEEE Trans. Syst., Man, Cybern.: Syst. 51 3725
 Google Scholar
Google Scholar
[7] Olasupo T O, Otero C E 2017 IEEE Trans. Syst., Man, Cybern.: Syst. 50 256
 Google Scholar
Google Scholar
[8] Laitila P, Virtanen K 2018 IEEE Trans. Syst., Man, Cybern.: Syst. 50 1943
 Google Scholar
Google Scholar
[9] Yang J, Yao C, Ma W, Chen G 2010 Physica A 389 859
 Google Scholar
Google Scholar
[10] Morone F, Makse H A 2015 Nature 524 65
 Google Scholar
Google Scholar
[11] Guo C, Li W M, Liu F F, Zhong K X, Wu X, Zhao Y G, Jin Q 2024 Neurocomputing 564 126936
 Google Scholar
Google Scholar
[12] Kempe D, Kleinberg J, Tardos É 2003 Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Washington, DC, USA, August 24–27, 2003 p137
[13] Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N 2007 Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining San Jose, CA, USA, August 12–15, 2007 p420
[14] Ou Z, Wang S 2024 Swarm Evol. Comput. 87 101542
 Google Scholar
Google Scholar
[15] Kumar S, Mallik A, Panda B S 2023 Expert Syst. Appl. 212 118770
 Google Scholar
Google Scholar
[16] Albert R, Jeong H, Barabási A L 1999 Nature 401 130
 Google Scholar
Google Scholar
[17] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
 Google Scholar
Google Scholar
[18] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
 Google Scholar
Google Scholar
[19] Hage P, Harary F 1995 Soc. Netw. 17 57
 Google Scholar
Google Scholar
[20] Dolev S, Elovici Y, Puzis R 2010 J. ACM 57 25
 Google Scholar
Google Scholar
[21] Opsahl T, Agneessens F, Skvoretz J 2010 Social Networks 32 245
 Google Scholar
Google Scholar
[22] Katz L 1953 Psychometrika 18 39
 Google Scholar
Google Scholar
[23] Wang Y, Zheng Y N, Shi X L, Liu Y G 2022 Physica A 588 126535
 Google Scholar
Google Scholar
[24] Zhao Z L, Liu X P, Sun Y, Zhao N N, Hu A H, Wang S L, Tu Y Y 2025 Chaos, Solitons Fractals 193 116078
 Google Scholar
Google Scholar
[25] Chen W, Wang Y J, Yang S Y 2009 Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Paris, France, June 28–July 1 p199
[26] Berahmand K, Bouyer A, Samadi N 2019 Computing 101 1711
 Google Scholar
Google Scholar
[27] Salavati C, Abdollahpouri A, Manbari Z 2019 Neurocomputing 336 36
 Google Scholar
Google Scholar
[28] Wen T, Deng Y 2020 Inf. Sci. 512 549
 Google Scholar
Google Scholar
[29] Yang P L, Zhao L J, Dong C, Xu G Q, Zhou L X 2023 Chin. Phys. B 32 058901
 Google Scholar
Google Scholar
[30] Zhang J X, Chen D B, Dong Q, Zhao Z D 2016 Sci. Rep. 6 27823
 Google Scholar
Google Scholar
[31] Li H Y, Wang X, Chen Y, Cheng S Y, Lu D J 2025 Sci. Rep. 15 1693
 Google Scholar
Google Scholar
[32] Sun H L, Chen D B, He J L, Ch’ng E 2019 Physica A 519 303
 Google Scholar
Google Scholar
[33] Kumar S, Panda B S 2020 Physica A 553 124215
 Google Scholar
Google Scholar
[34] Bae J H, Kim S W 2014 Physica A 395 549
 Google Scholar
Google Scholar
[35] Liu P, Li L, Fang S, Yao Y K 2021 Chaos, Solitons Fractals 152 111309
 Google Scholar
Google Scholar
[36] Wang, G. Alias S B, Sun Z J, Wang F F, Fan A W, Hu H F 2023 Heliyon 9 e16112
 Google Scholar
Google Scholar
[37] Jeh G, Widom J 2002 Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Edmonton, Canada, July 23–26, 2002 p538
[38] Chi K, Yin G S, Dong Y X, Dong H B 2019 Knowl-Based Syst. 181 104792
 Google Scholar
Google Scholar
[39] Rossi R, Ahmed N 2015 Proceedings of the 29th AAAI Conference on Artificial Intelligence Austin, TX, USA, January 25–30, 2015 p4292
[40] Batagelj V, Mrvar A 1998 Connections 21 47
[41] Blagus N, Šubelj L, Bajec M 2012 Physica A 391 2794
 Google Scholar
Google Scholar
[42] Jeong H, Tombor B, Albert R, Oltvai Z N, Barabási A L 2000 Nature 407 651
 Google Scholar
Google Scholar
[43] Kunegis J 2013 Proceedings of the 22nd International Conference on World Wide Web Rio de Janeiro, Brazil, May 13–17, 2013 p1343
[44] McAuley J, Leskovec J 2012 Advances in Neural Information Processing Systems (Lake Tahoe, USA: NIPS) p539
[45] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200
 Google Scholar
Google Scholar
[46] Ruan Y R, Liu S Z, Tang J , Guo Y M, Yu T Y 2025 Expert Syst. Appl. 268 126292
 Google Scholar
Google Scholar
[47] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowl-Based Syst. 198 105893
 Google Scholar
Google Scholar
[48] Zhang M, Wang X J, Jin L, Song M, Li Z Y 2022 Neurocomputing 497 13
 Google Scholar
Google Scholar
-
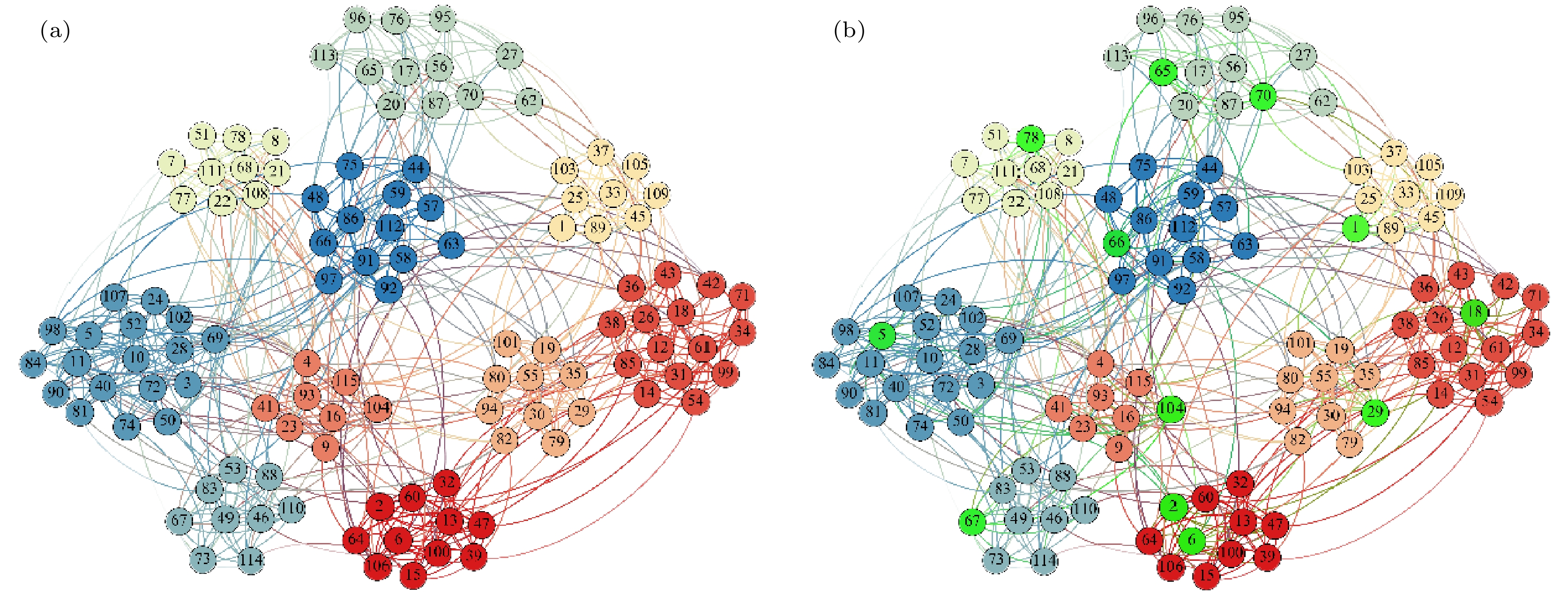
图 1 Football网络中的多影响力节点识别结果 (a) 网络划分情况, 不同社区用不同颜色表示; (b) 绿色节点为IMVoteRank方法选取的12个初始传播源
Figure 1. Identification results of multiple influential nodes in the Football network: (a) Network partitioning, with different communities represented by different colors; (b) the green nodes are the 12 initial propagation sources selected by the IMVoteRank method.
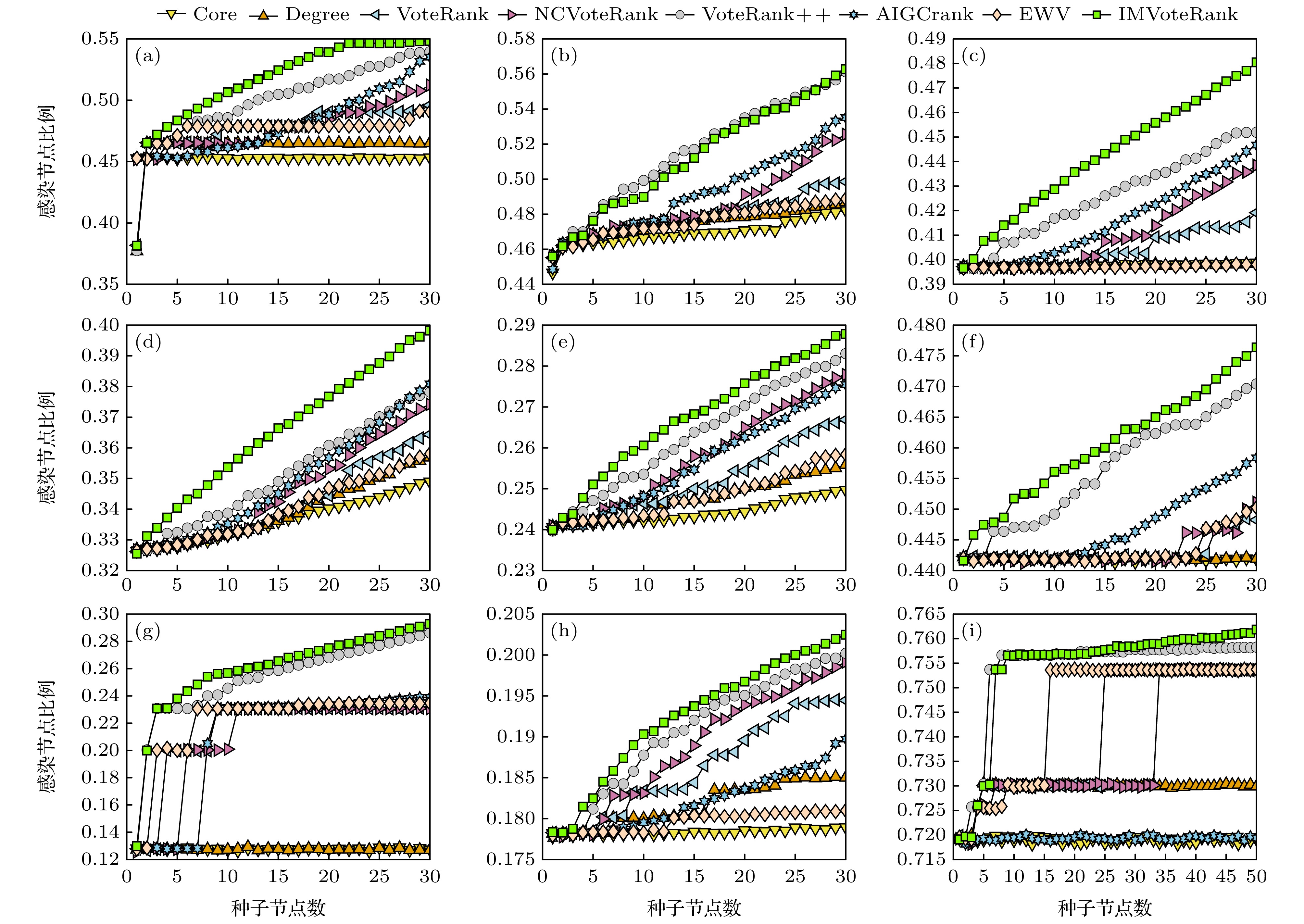
图 2 SIR疾病传播率β = 0.1时, 不同算法感染网络节点比例与传播源数量之间的关系 (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 2. Relationship between the proportion of network nodes infected by different algorithms and the number of transmission sources when the SIR disease transmission rate β = 0.1: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined.
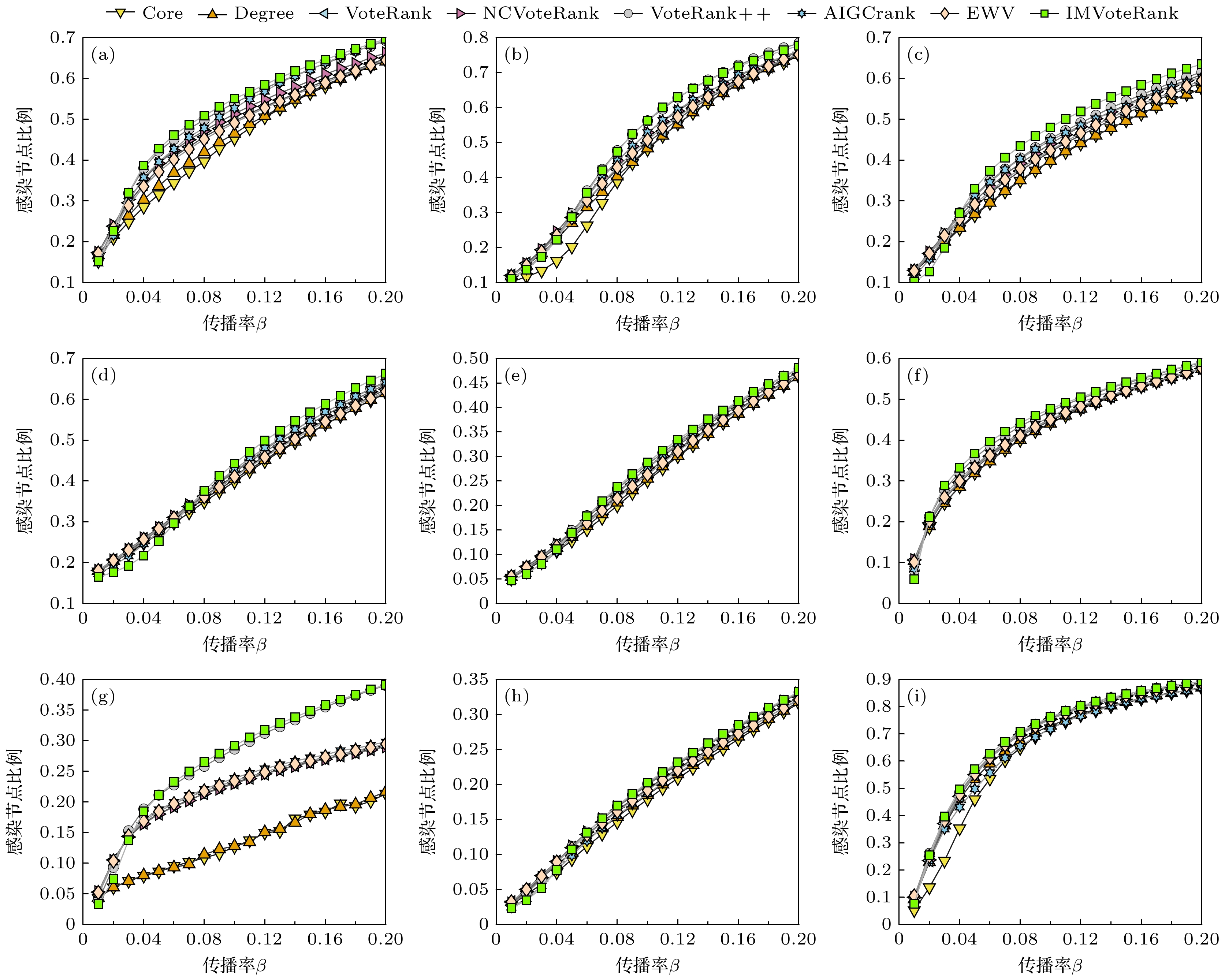
图 3 传播源数量固定时, 不同算法感染网络节点比例与SIR疾病传播率之间的关系(Facebook_combined网络中初始传播源数量为50, 其他8个网络的传播源节点数量为30) (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 3. Relationship between the proportion of network nodes infected by different algorithms and the SIR disease transmission rate when the number of transmission sources is fixed: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined. The initial number of propagation sources in the Facebook_combined network is 50, while the number of propagation source nodes in the other eight networks is 30.
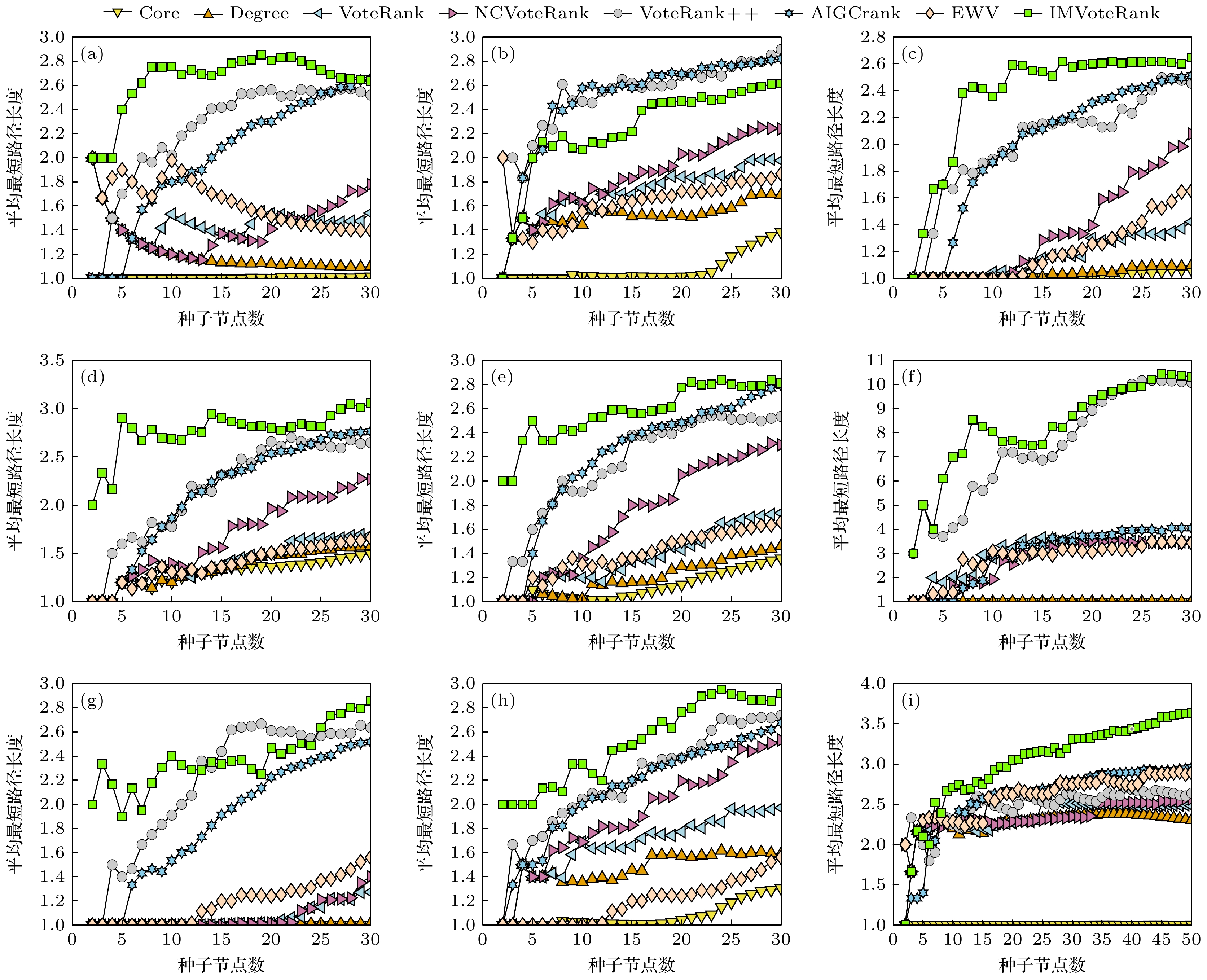
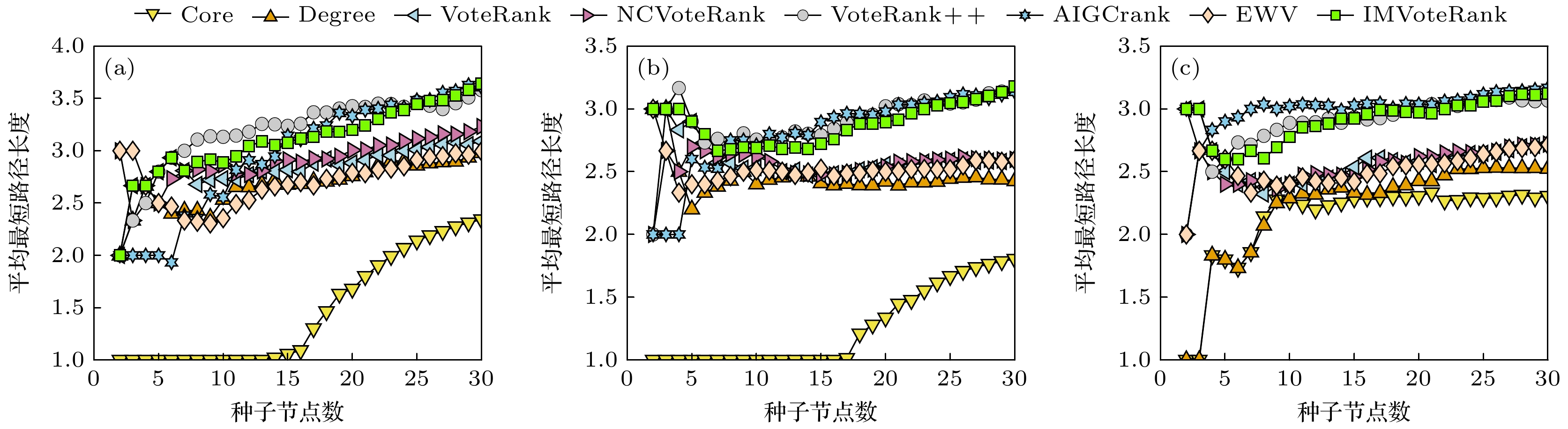
图 4 七种方法选取的传播源之间的平均路径长度与传播源数量间的关系 (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 4. Relationship between the average path length and the number of propagation sources selected by seven methods: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined.
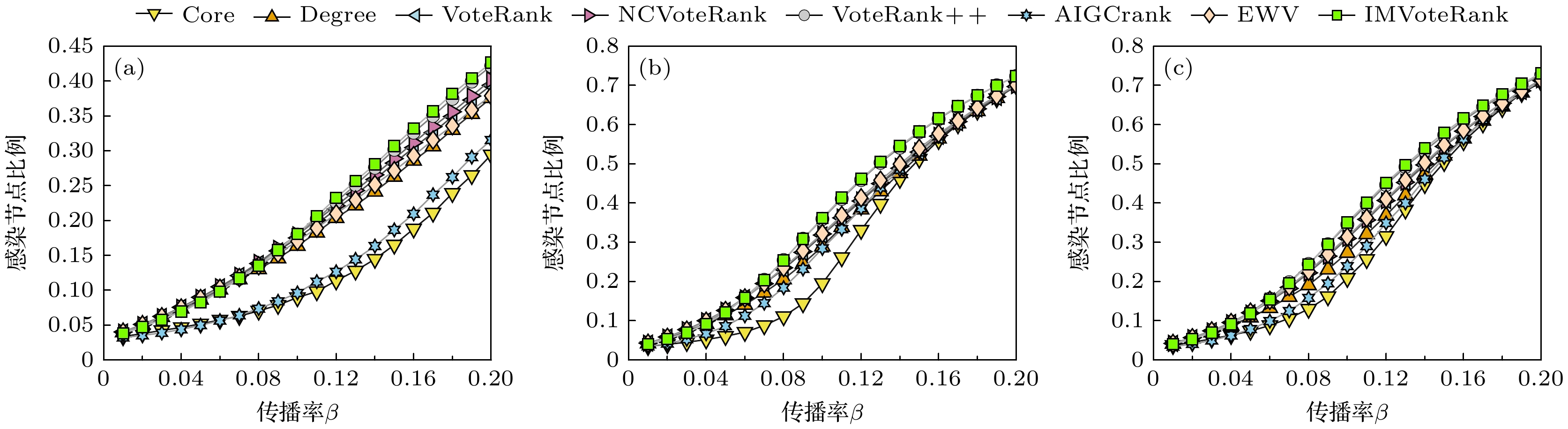
图 5 LFR 人工数据集中各方法所选初始种子节点在不同信息传播率β下感染节点比例对比 (a) $\left\langle k \right\rangle = 5$; (b) $\left\langle k \right\rangle = 10$; (c)$\left\langle k \right\rangle = 15$
Figure 5. Comparison of the proportion of infected nodes selected by each method as initial seed nodes in the LFR artificial dataset under different information transmission rates: (a) $\left\langle k \right\rangle = 5$; (b) $\left\langle k \right\rangle = 10$; (c) $\left\langle k \right\rangle = 15$.
图 6 LFR人工数据集中8种方法选取的传播源之间的平均路径长度与传播源数量间的关系 (a) $\left\langle k \right\rangle = 5$; (b) $\left\langle k \right\rangle = 10$; (c)$\left\langle k \right\rangle = 15$
Figure 6. Relationship between the average path length of the spread sources selected by eight methods in the LFR artificial dataset and the number of spread sources: (a) $\left\langle k \right\rangle = 5$; (b) $\left\langle k \right\rangle = 10$; (c) $\left\langle k \right\rangle = 15$.
表 1 计算步骤
Table 1. Step of the calculation.
输入: 网络$ G\left( {V, E} \right) $, 需要选择的种子节点数r, 调节参数θ
输出: 包含r个有影响力节点的集合SN//初始化
1 foreach v in V do
2 (S(u), Va(u)) = (0, 1)
3 end foreach
//迭代选择种子节点
4 while $ \left| {SN} \right| < r $ do
5 foreach u in V do
6 foreach v in N(u) do
7 $ VP(u, v) = (1 - \theta ){V_{\text{a}}}(u) + \theta {V_{\text{a}}}(u) {{|N(u) \cap N(v)|}}/{{{k_v}}} $
8 $ S\left( v \right) = S\left( v \right) + VP\left( {u, v} \right) $ //节点v收到的投票得分增加
9 end foreach
10 end foreach
11 $ {v_{{\text{max}}}} = {\text{ argmax}}(S\left( v \right)) $//选择投票得分最高的节点vmax
// 动态群组隔离策略
12 OG = {vmax}
13 foreach u in N(vmax) do
14 if $ \left| {N\left( {{v_{{\text{max}}}}} \right) \cap N\left( u \right)} \right|/\left\langle k \right\rangle \geqslant 1 $ then
15 OG = OG∪{u}
16 end if
17 end foreach
// 扩展群组
19 foreach i in sort(N(OG), by degree desc) do
20 if $ k_i^{{\text{in}}}({\text{OG}}) $ ≥ $ k_i^{{\text{out}}}({\text{OG}}) $ then
21 OG = OG ∪{i}
22 end if
23 end foreach
// 隔离群组
24 foreach node i in OG do
25 Va(i) = 0//将群组内所有节点的投票能力设为0
//将网络邻接矩阵中该节点对应的行和列置为0
26 foreach j in V do
27 adj_matrix[i][j] = 0
28 adj_matrix[j][i] = 0
29 end foreach
30 end foreach
31 foreach neighbor j of vmax not in OG
32 $ {V_a}(j) = {V_a}\left( j \right)/2 $
33 end foreach
34 SN = SN ∪{vmax}
35 end while
36 return SN
表 2 真实网络参数描述
Table 2. Parameters description of real networks.
网络 N E $\left\langle d \right\rangle $ $\left\langle k \right\rangle $ C βth ksmax ksmin ECON-WM3 257 2379 2.6147 18.5136 0.2653 0.0207 33 1 Facebook-SZ 324 2218 3.0537 13.691 0.4658 0.0466 18 1 USAir 332 2126 2.738 12.807 0.6252 0.0225 26 1 Celegans 453 2025 2.6638 8.9404 0.6465 0.0249 10 1 ASOIAF 796 2823 3.4162 7.093 0.4859 0.0336 13 1 Dnc-corecipient 849 10384 2.7595 24.4617 0.5072 0.0107 74 1 ERIS1176 1174 8687 12.0591 14.799 0.4327 0.0190 79 1 DNC-emails 1833 39264 3.3695 4.7938 0.2157 0.0135 17 1 Facebook-combined 4039 88234 3.6925 43.691 0.6055 0.0094 115 1 -
[1] Watts D J, Strogatz S H 1998 Nature 393 440
 Google Scholar
Google Scholar
[2] Barabasi A L, Albert R 1999 Science 286 509
 Google Scholar
Google Scholar
[3] Liu Y Y, Slotine J J, Barabasi A L 2011 Nature 473 167
 Google Scholar
Google Scholar
[4] Yang Z, Li Y, Liu J 2021 Proceedings of the 15th EAI International Conference on Communications and Networking (ChinaCom 2020) Shanghai, China, November 20–21, 2020 p766
[5] Li Y G, Xiao Z L, Gao A, Wu W N, Pei E R 2025 Knowl-Based Syst. 317 113434
 Google Scholar
Google Scholar
[6] Lin Y G, Wang X M, Hao F, Jiang Y C, Wu Y L, Min G Y, He D J, Zhu S C, Zhao W 2019 IEEE Trans. Syst., Man, Cybern.: Syst. 51 3725
 Google Scholar
Google Scholar
[7] Olasupo T O, Otero C E 2017 IEEE Trans. Syst., Man, Cybern.: Syst. 50 256
 Google Scholar
Google Scholar
[8] Laitila P, Virtanen K 2018 IEEE Trans. Syst., Man, Cybern.: Syst. 50 1943
 Google Scholar
Google Scholar
[9] Yang J, Yao C, Ma W, Chen G 2010 Physica A 389 859
 Google Scholar
Google Scholar
[10] Morone F, Makse H A 2015 Nature 524 65
 Google Scholar
Google Scholar
[11] Guo C, Li W M, Liu F F, Zhong K X, Wu X, Zhao Y G, Jin Q 2024 Neurocomputing 564 126936
 Google Scholar
Google Scholar
[12] Kempe D, Kleinberg J, Tardos É 2003 Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Washington, DC, USA, August 24–27, 2003 p137
[13] Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N 2007 Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining San Jose, CA, USA, August 12–15, 2007 p420
[14] Ou Z, Wang S 2024 Swarm Evol. Comput. 87 101542
 Google Scholar
Google Scholar
[15] Kumar S, Mallik A, Panda B S 2023 Expert Syst. Appl. 212 118770
 Google Scholar
Google Scholar
[16] Albert R, Jeong H, Barabási A L 1999 Nature 401 130
 Google Scholar
Google Scholar
[17] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
 Google Scholar
Google Scholar
[18] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168
 Google Scholar
Google Scholar
[19] Hage P, Harary F 1995 Soc. Netw. 17 57
 Google Scholar
Google Scholar
[20] Dolev S, Elovici Y, Puzis R 2010 J. ACM 57 25
 Google Scholar
Google Scholar
[21] Opsahl T, Agneessens F, Skvoretz J 2010 Social Networks 32 245
 Google Scholar
Google Scholar
[22] Katz L 1953 Psychometrika 18 39
 Google Scholar
Google Scholar
[23] Wang Y, Zheng Y N, Shi X L, Liu Y G 2022 Physica A 588 126535
 Google Scholar
Google Scholar
[24] Zhao Z L, Liu X P, Sun Y, Zhao N N, Hu A H, Wang S L, Tu Y Y 2025 Chaos, Solitons Fractals 193 116078
 Google Scholar
Google Scholar
[25] Chen W, Wang Y J, Yang S Y 2009 Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Paris, France, June 28–July 1 p199
[26] Berahmand K, Bouyer A, Samadi N 2019 Computing 101 1711
 Google Scholar
Google Scholar
[27] Salavati C, Abdollahpouri A, Manbari Z 2019 Neurocomputing 336 36
 Google Scholar
Google Scholar
[28] Wen T, Deng Y 2020 Inf. Sci. 512 549
 Google Scholar
Google Scholar
[29] Yang P L, Zhao L J, Dong C, Xu G Q, Zhou L X 2023 Chin. Phys. B 32 058901
 Google Scholar
Google Scholar
[30] Zhang J X, Chen D B, Dong Q, Zhao Z D 2016 Sci. Rep. 6 27823
 Google Scholar
Google Scholar
[31] Li H Y, Wang X, Chen Y, Cheng S Y, Lu D J 2025 Sci. Rep. 15 1693
 Google Scholar
Google Scholar
[32] Sun H L, Chen D B, He J L, Ch’ng E 2019 Physica A 519 303
 Google Scholar
Google Scholar
[33] Kumar S, Panda B S 2020 Physica A 553 124215
 Google Scholar
Google Scholar
[34] Bae J H, Kim S W 2014 Physica A 395 549
 Google Scholar
Google Scholar
[35] Liu P, Li L, Fang S, Yao Y K 2021 Chaos, Solitons Fractals 152 111309
 Google Scholar
Google Scholar
[36] Wang, G. Alias S B, Sun Z J, Wang F F, Fan A W, Hu H F 2023 Heliyon 9 e16112
 Google Scholar
Google Scholar
[37] Jeh G, Widom J 2002 Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Edmonton, Canada, July 23–26, 2002 p538
[38] Chi K, Yin G S, Dong Y X, Dong H B 2019 Knowl-Based Syst. 181 104792
 Google Scholar
Google Scholar
[39] Rossi R, Ahmed N 2015 Proceedings of the 29th AAAI Conference on Artificial Intelligence Austin, TX, USA, January 25–30, 2015 p4292
[40] Batagelj V, Mrvar A 1998 Connections 21 47
[41] Blagus N, Šubelj L, Bajec M 2012 Physica A 391 2794
 Google Scholar
Google Scholar
[42] Jeong H, Tombor B, Albert R, Oltvai Z N, Barabási A L 2000 Nature 407 651
 Google Scholar
Google Scholar
[43] Kunegis J 2013 Proceedings of the 22nd International Conference on World Wide Web Rio de Janeiro, Brazil, May 13–17, 2013 p1343
[44] McAuley J, Leskovec J 2012 Advances in Neural Information Processing Systems (Lake Tahoe, USA: NIPS) p539
[45] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200
 Google Scholar
Google Scholar
[46] Ruan Y R, Liu S Z, Tang J , Guo Y M, Yu T Y 2025 Expert Syst. Appl. 268 126292
 Google Scholar
Google Scholar
[47] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowl-Based Syst. 198 105893
 Google Scholar
Google Scholar
[48] Zhang M, Wang X J, Jin L, Song M, Li Z Y 2022 Neurocomputing 497 13
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 1903
- PDF Downloads: 45
- Cited By: 0














 DownLoad:
DownLoad: