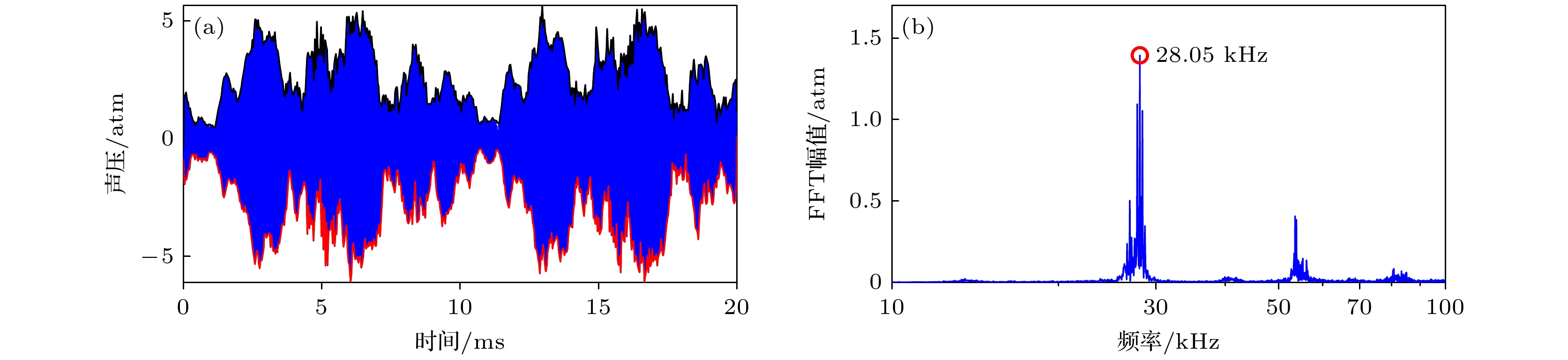
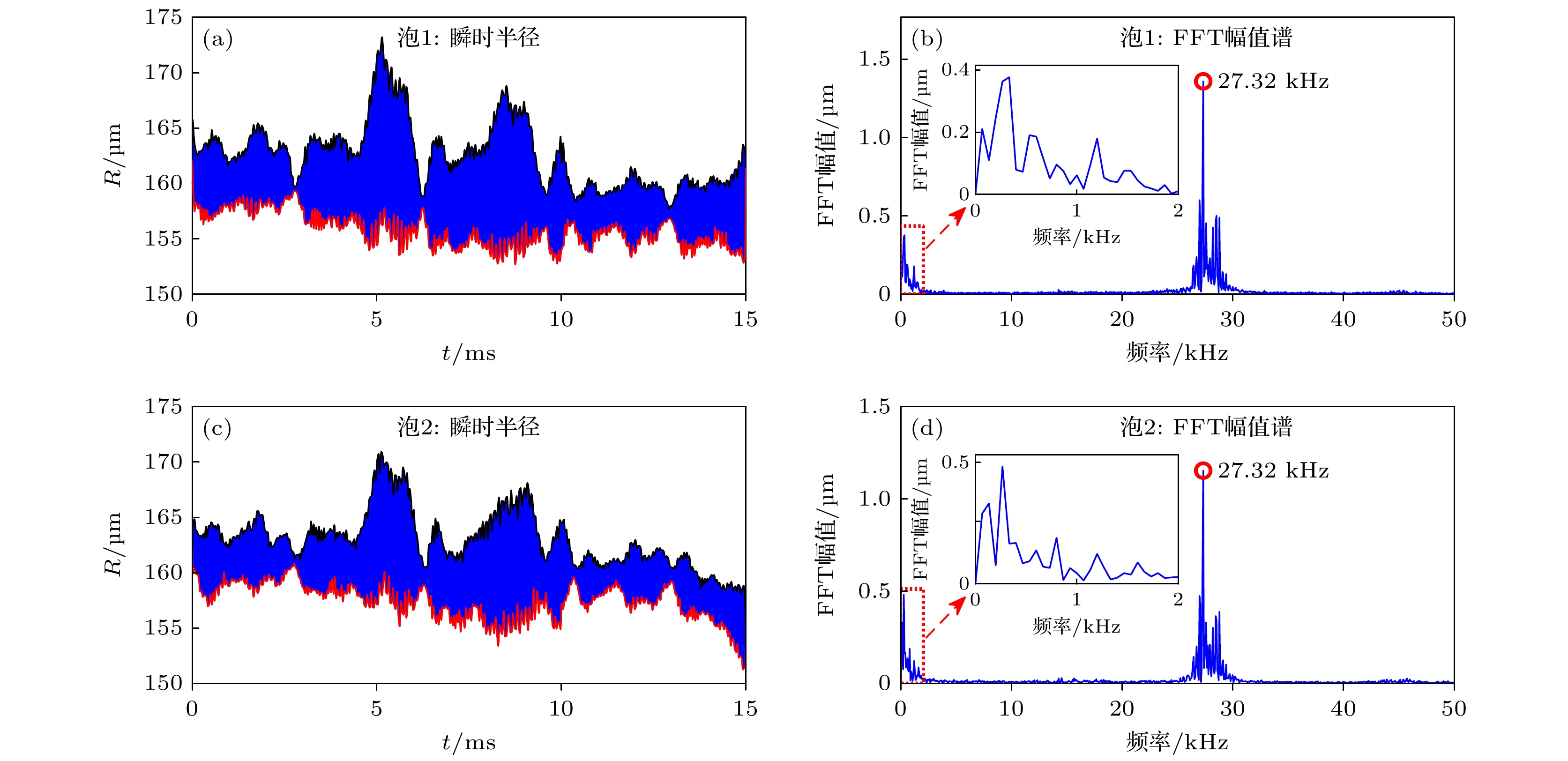
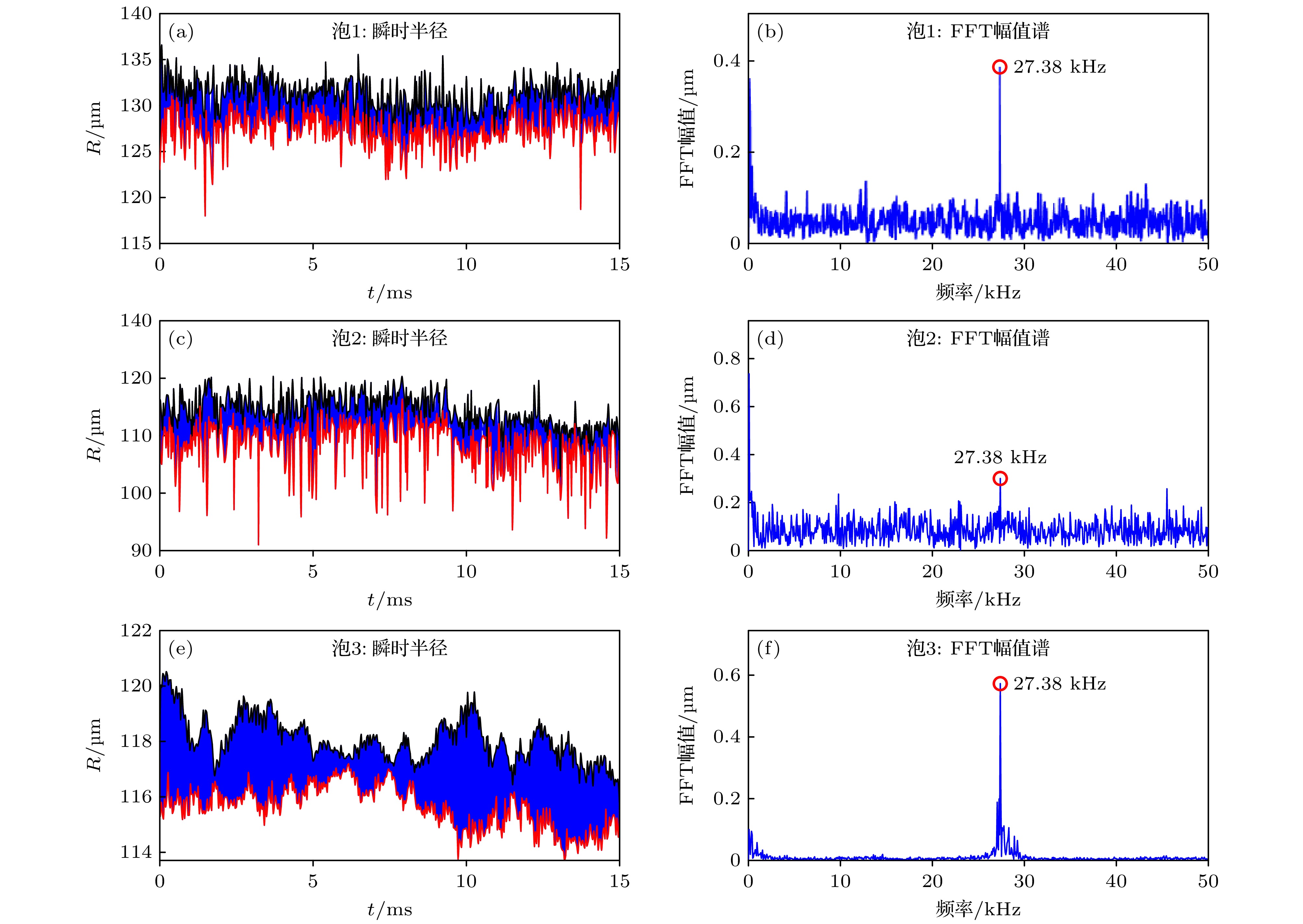
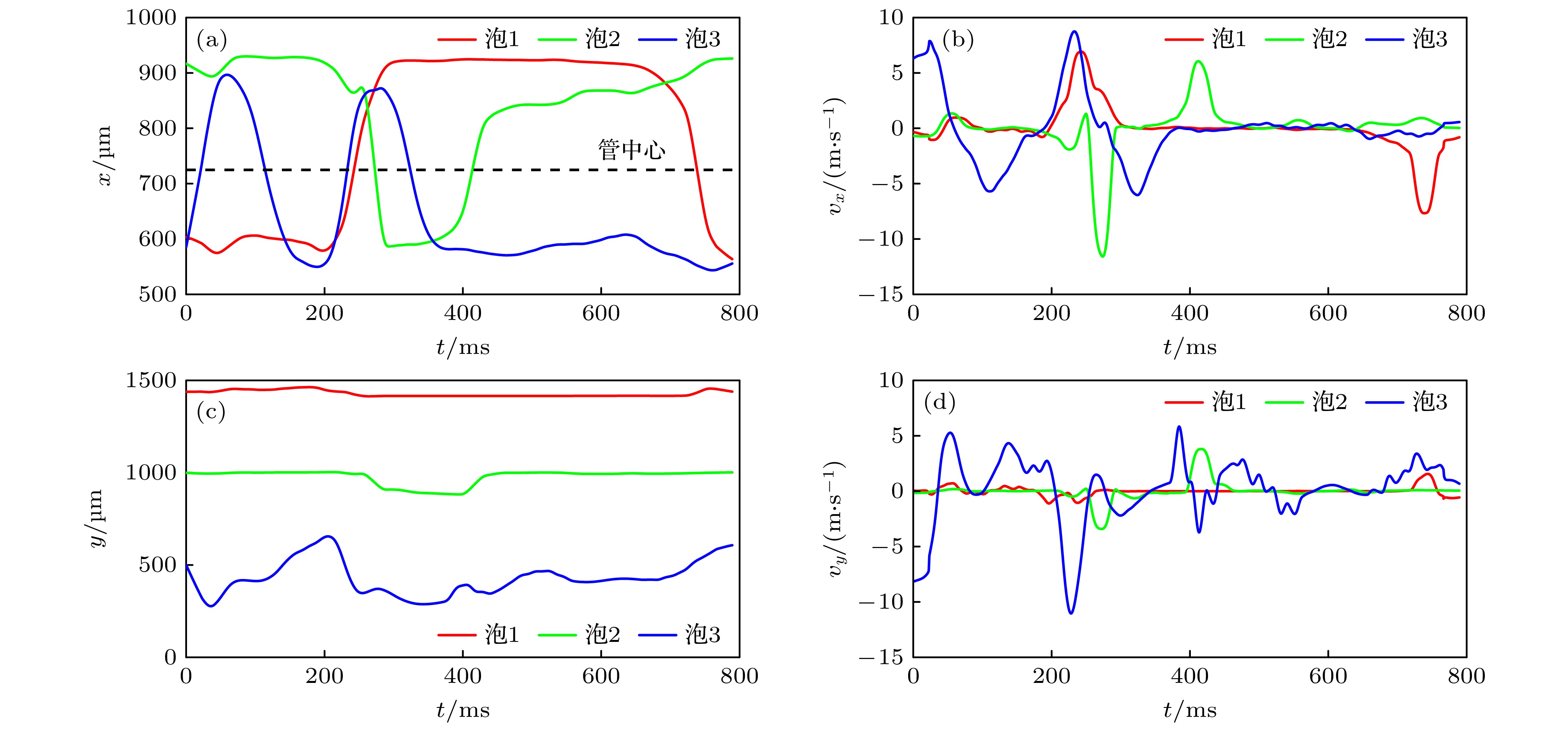
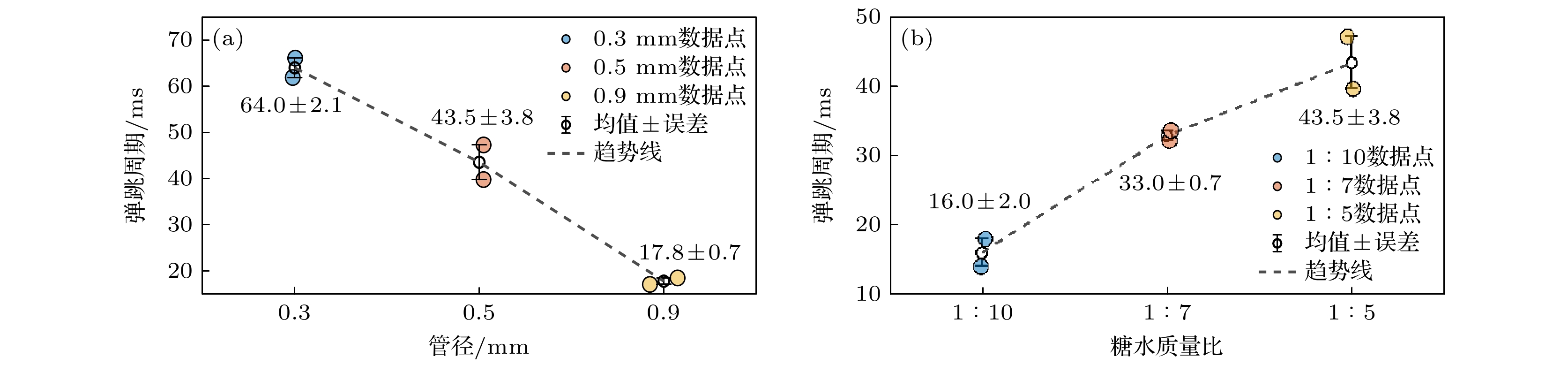
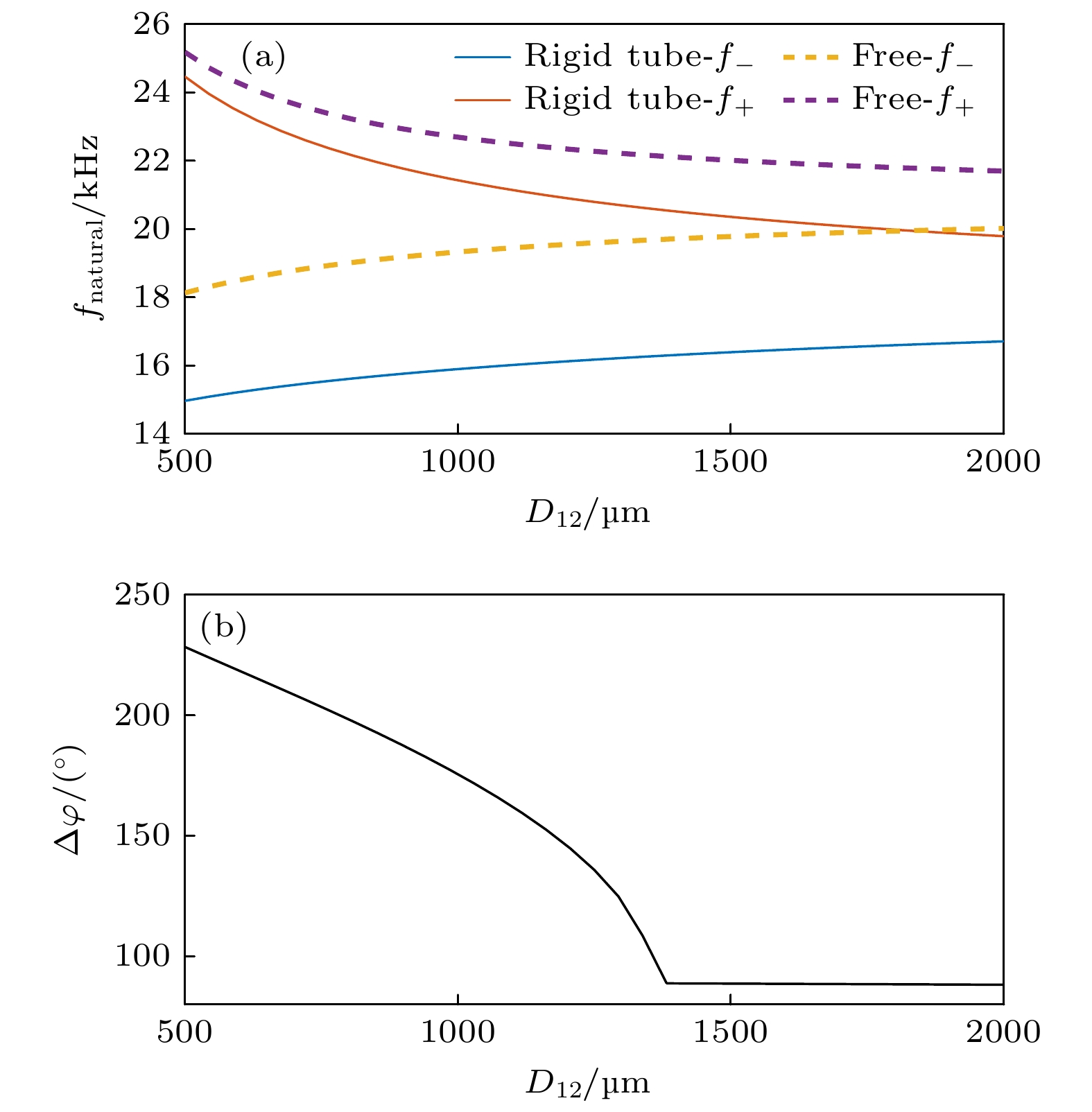
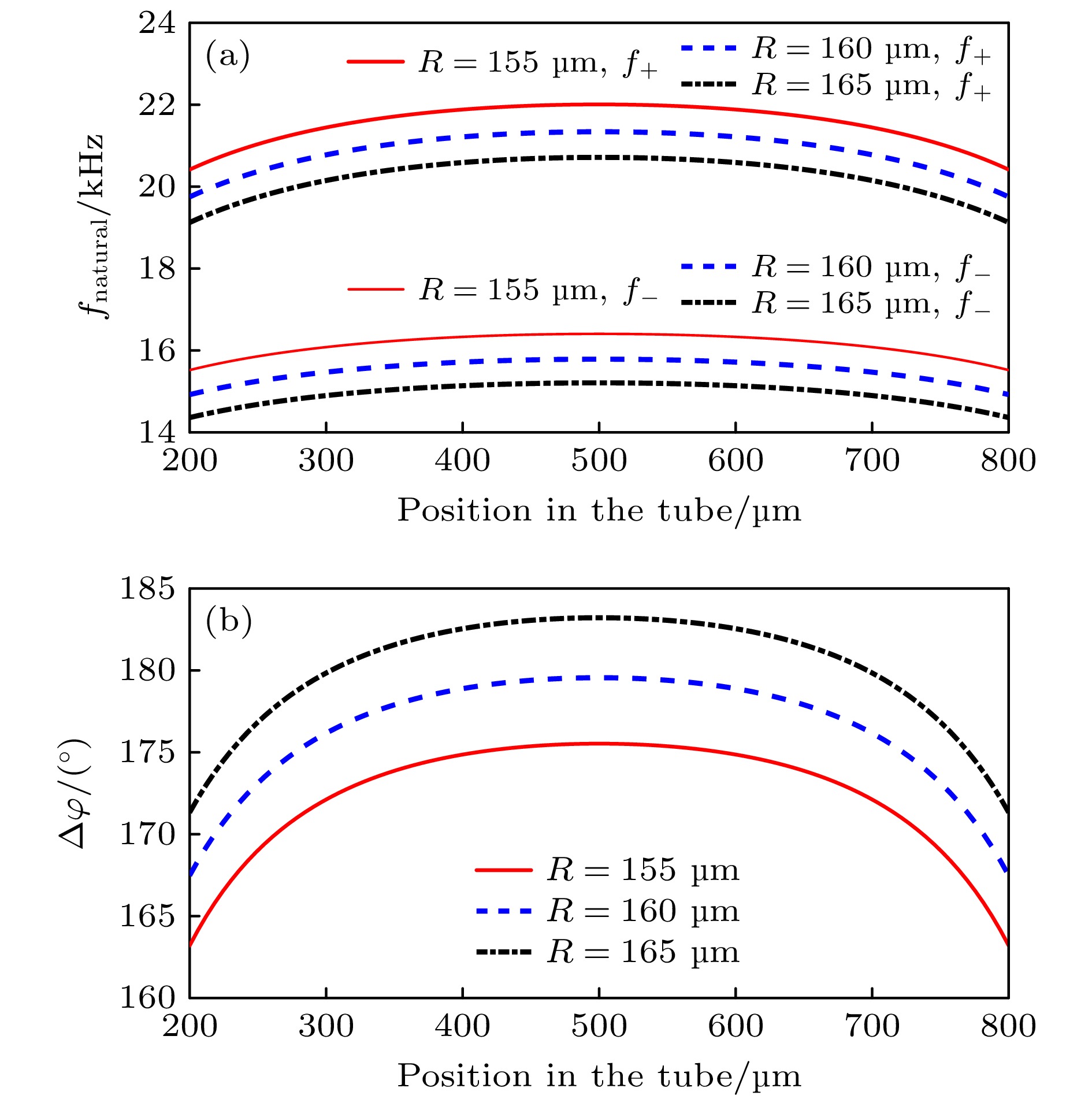
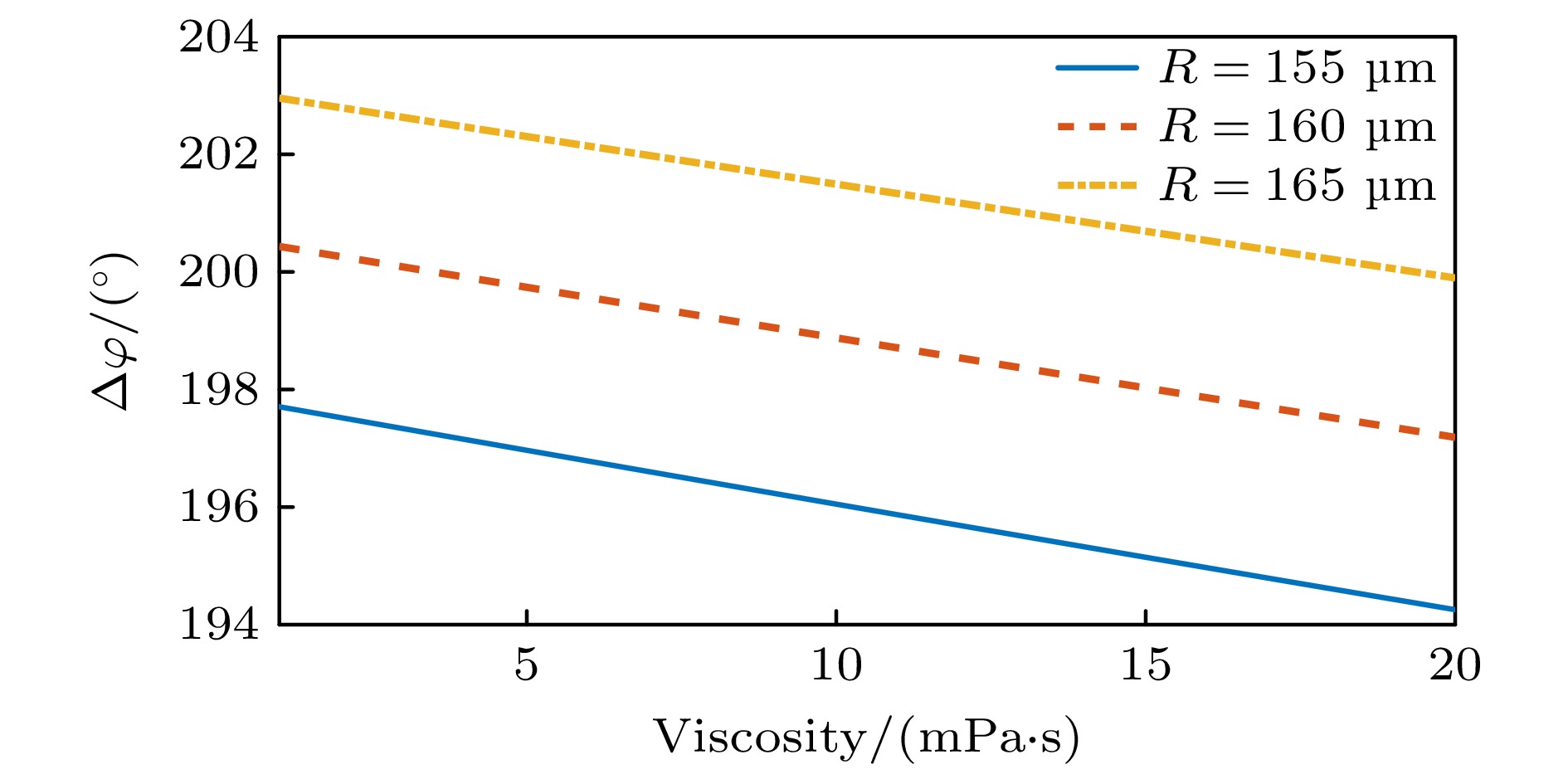
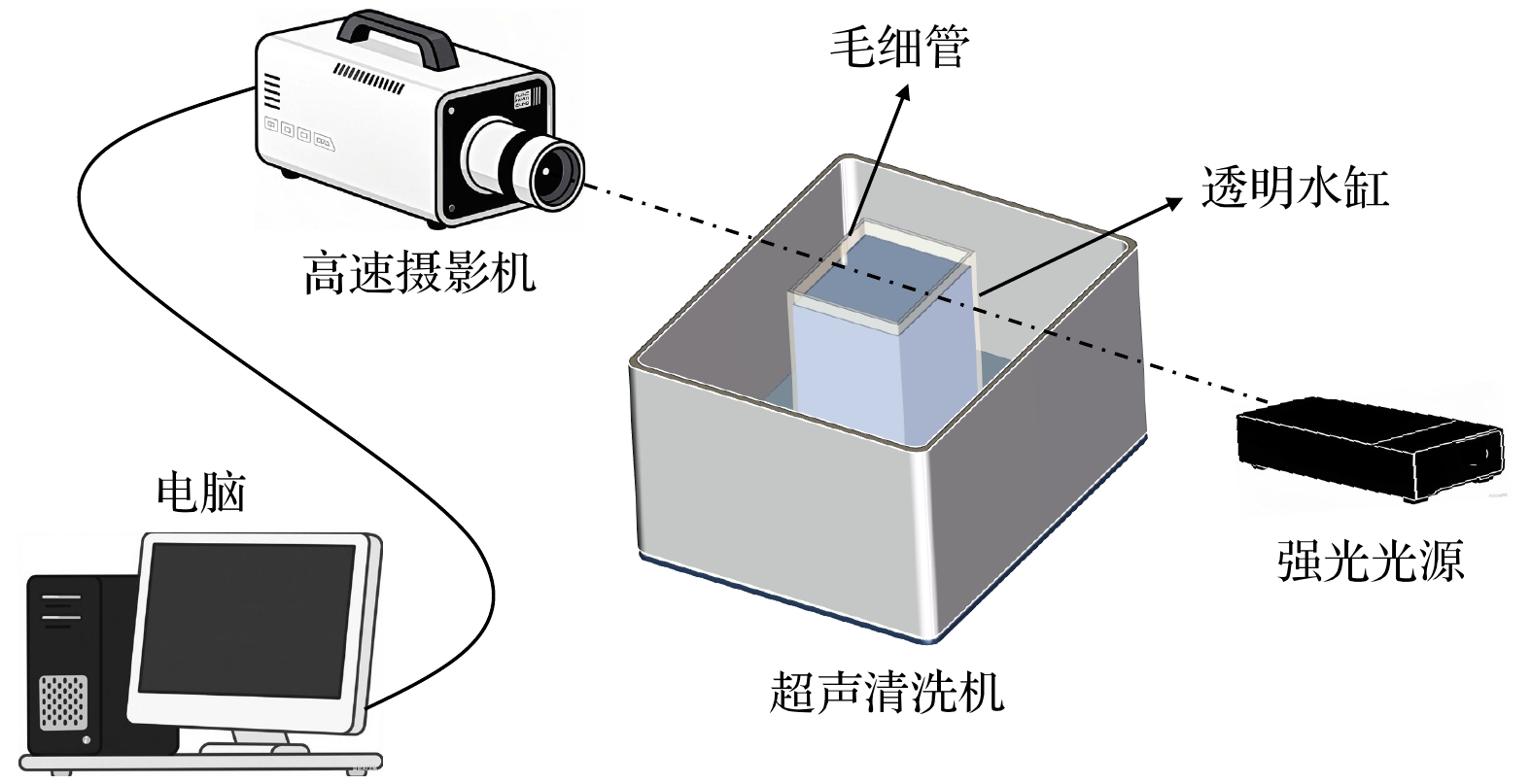
-
This study systematically investigates the bouncing behavior and dynamics of microbubbles under ultrasound excitation within a rigid capillary in order to offer quantitative insights into their oscillation characteristics, migration trajectories, and phase modulation mechanisms for applications in microfluidics, contrast-enhanced ultrasound imaging, and controlled drug delivery. A high-speed imaging system is employed to track the motion of single-, double-, and triple-bubble systems in a viscoelastic medium inside a capillary with a 0.5-mm inner diameter. Under a 28-kHz ultrasound field, bubble dynamics are captured at 100,000 frames per second. Image processing techniques, including dynamic threshold segmentation and morphological operations, are employed to extract bubble contours and centroid trajectories. Spectral analysis via fast Fourier transform (FFT) is performed to identify oscillation frequencies and modulation characteristics. Experimental results show that a single bubble undergoes periodic lateral migration, with oscillation frequency slightly below the driving frequency, and that sideband distribution in its spectrum is asymmetric. In the two-bubble system, five different dynamic stages are identified: initial suppression, accelerated migration, interaction dominance, position exchange, and a secondary approach to the wall. The bubbles oscillate at a common dominant frequency of 27.32 kHz but maintain phase difference. Modulation sidebands of approximately 0.3 kHz are observed, indicating nonlinear coupling. The three-bubble system exhibits more complex spatiotemporal evolution, including sequential migration and transitions between triangular and mirror-symmetric configurations. A notable sideband at 0.1 kHz suggests that multi-bubble synergy enhances nonlinear behavior. The tube diameter and fluid viscosity are found to influence the bouncing period through added mass effects and viscous energy dissipation, respectively. The period increases significantly with tube diameter decreasing, and decreases with fluid viscosity lessening. Theoretical modeling incorporates the mirror bubble effect into the coupled Keller-Miksis equations to account for wall confinement, thus successfully simulating the oscillation and translation of confined microbubbles. Numerical analysis further indicates that inter-bubble distance, wall proximity, and medium viscosity modulate the dynamic behavior of the system. Specifically, the bubble resonance frequency is regulated by inter-bubble distance and wall confinement. The two-bubble system exhibits both in-phase and out-of-phase modes, with the latter being more sensitive to distance variation. Near the wall, the oscillation frequency decreases, and the phase difference attenuation accelerates. Increasing medium viscosity will weaken the phase coupling between bubbles, an effect which is particularly evident for smaller bubbles. This study not only enhances the understanding of multi-bubble synergistic effects in confined spaces but also provides a theoretical foundation and technical reference for optimizing ultrasound contrast agents, designing microfluidic devices, and developing targeted therapies in biomedicine.
-
Keywords:
- microbubbles /
- bouncing behavior /
- wall confinement /
- multibubble interaction
-
图 1 实验装置图像
Figure 1. Experimental setup schematic.
图 2 超声场信号 (a) 波形图; (b) 信号幅度谱
Figure 2. Ultrasonic field signals: (a) Waveform diagram; (b) signal amplitude spectrum.
图 3 单泡在管内弹跳的连续时序图像
Figure 3. Sequential images of single bubble bouncing in the capillary tube.
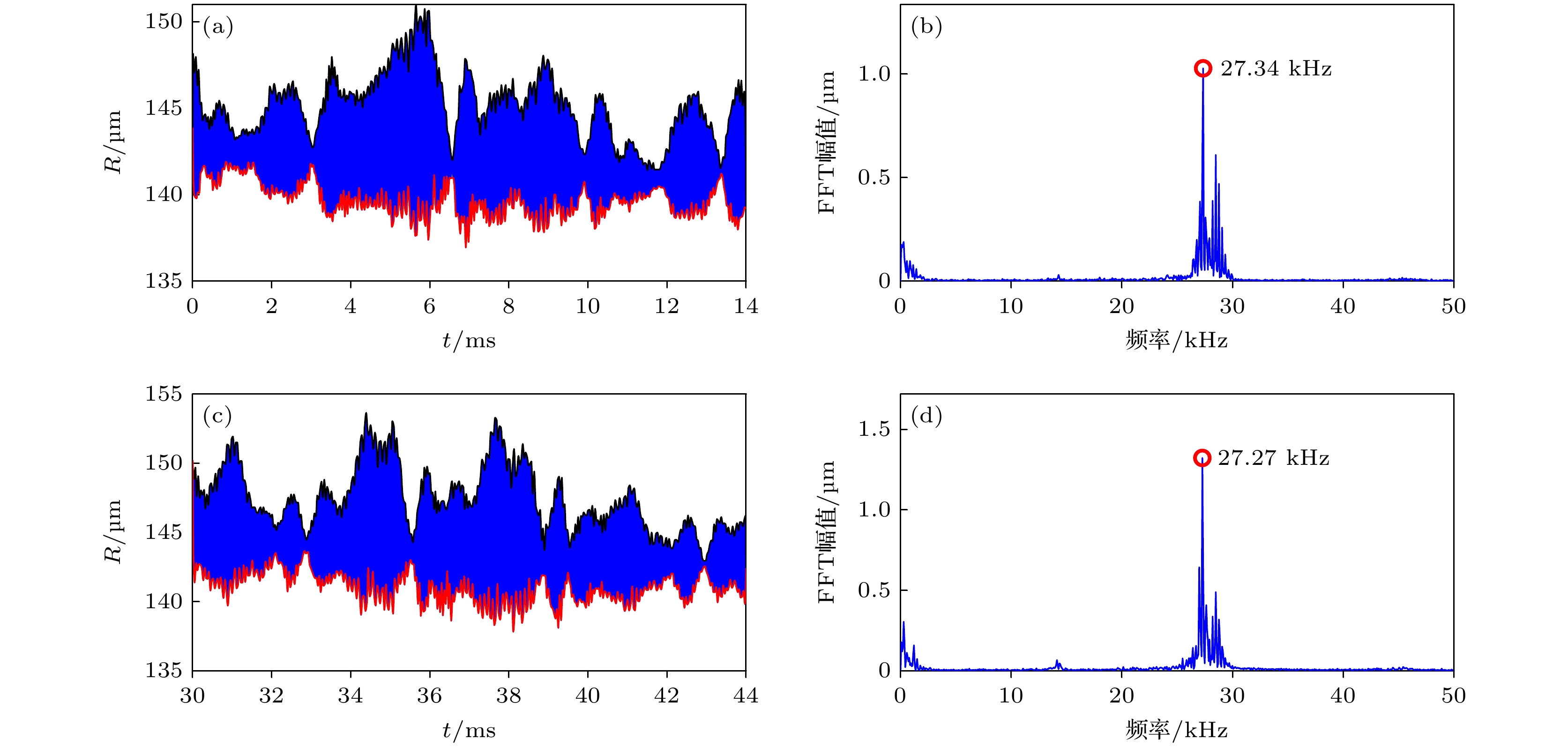
图 4 不同时段单泡振荡行为 (a) 0—14 ms半径时域变化; (b) 0—14 ms频谱分析; (c) 30—44 ms半径时域变化; (d) 30—44 ms频谱分析
Figure 4. Oscillation behavior of single bubble at different time intervals: (a) Radius temporal variation during 0–14 ms; (b) spectral analysis during 0–14 ms; (c) radius temporal variation during 30–44 ms; (d) spectral analysis during 30–44 ms.
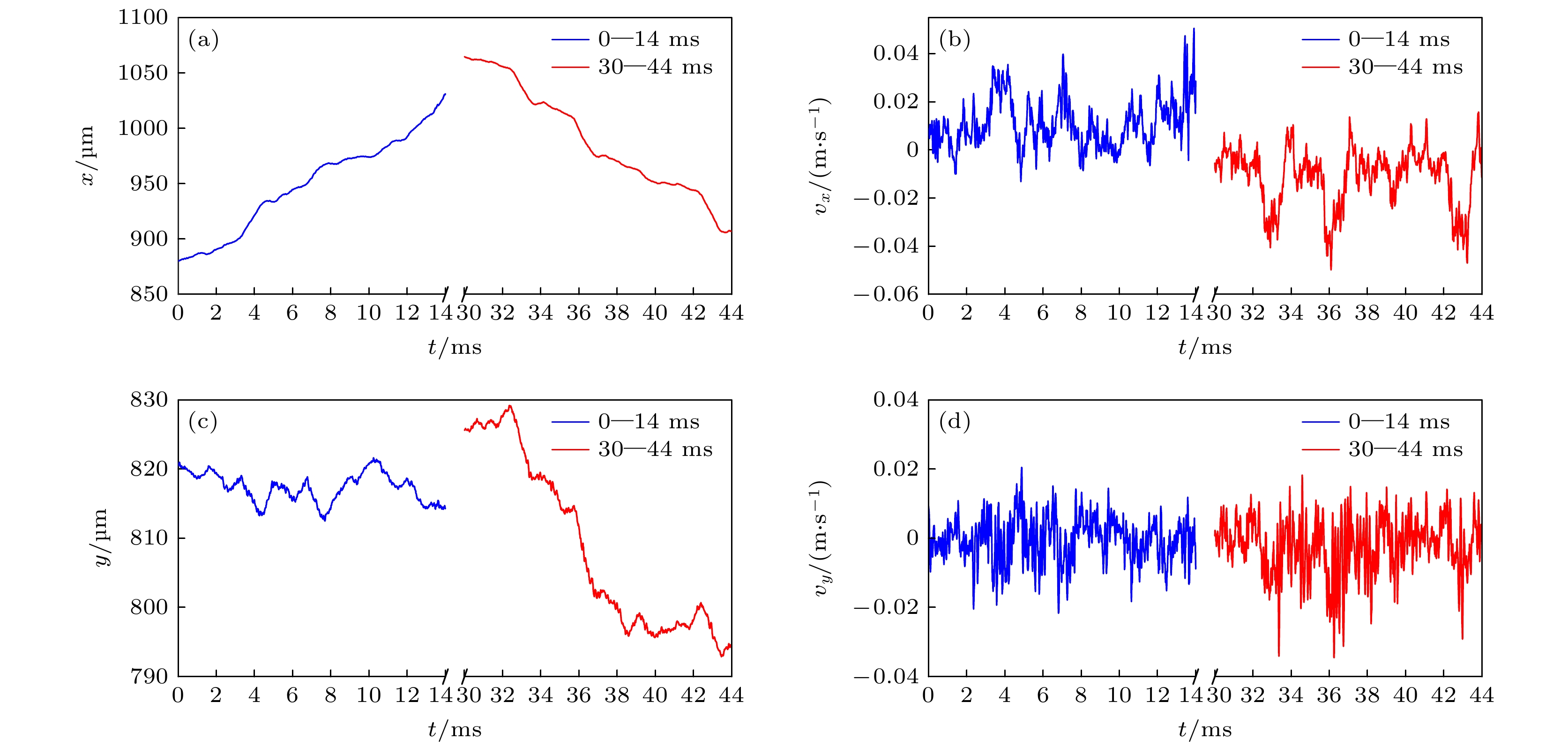
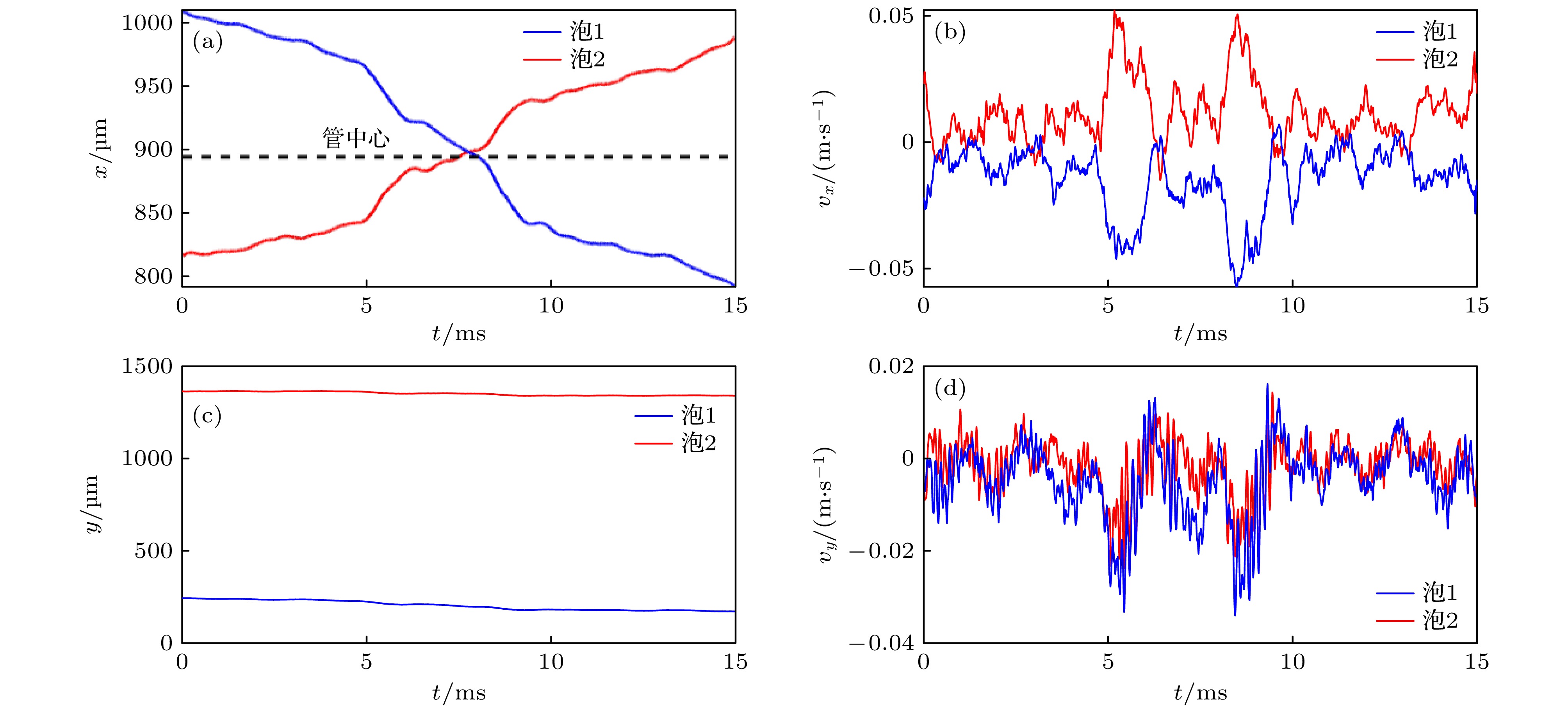
图 5 不同时段单泡平动行为 (a) 0—14 ms时段x方向位移; (b) 0—14 ms时段x方向速度; (c) 30—44 ms时段y方向位移; (d) 30—44 ms时段y方向速度
Figure 5. Translational behavior of single bubble at different time intervals: (a) x-direction displacement during 0–14 ms; (b) x-direction velocity during 0–14 ms; (c) y-direction displacement during 30–44 ms; (d) y-direction velocity during 30–44 ms.
图 6 双泡在管内弹跳的连续时序图像
Figure 6. Sequential images of dual-bubble bouncing in the capillary tube.
图 7 双泡半径时域变化(a), (c)及频谱分析(b), (d)
Figure 7. (a), (c) Temporal radius variations and (b), (d) spectral analysis of dual-bubble system.
图 8 两泡在管内弹跳的(a), (c)位置及(b), (d)速度变化
Figure 8. (a), (c) Position and (b), (d) velocity variations of two bubbles bouncing in the tube.
图 9 三泡在管内弹跳的连续时序图像
Figure 9. Sequential images of triple-bubble bouncing in the capillary tube.
图 10 三泡半径时域图(a), (c), (e)及频谱分析(b), (d), (f)
Figure 10. (a), (c), (e) Temporal radius profiles and (b), (d), (f) spectral analysis of triple-bubble system.
图 11 三泡在管内弹跳的(a), (c)位置及(b), (d)速度变化
Figure 11. (a), (c) Position and (b), (d) velocity variations of three bubbles bouncing in the tube.
图 12 (a)管径及(b)黏度对单泡弹跳周期的影响
Figure 12. Effects of (a) tube diameter and (b) viscosity on the period of single bubble bouncing.
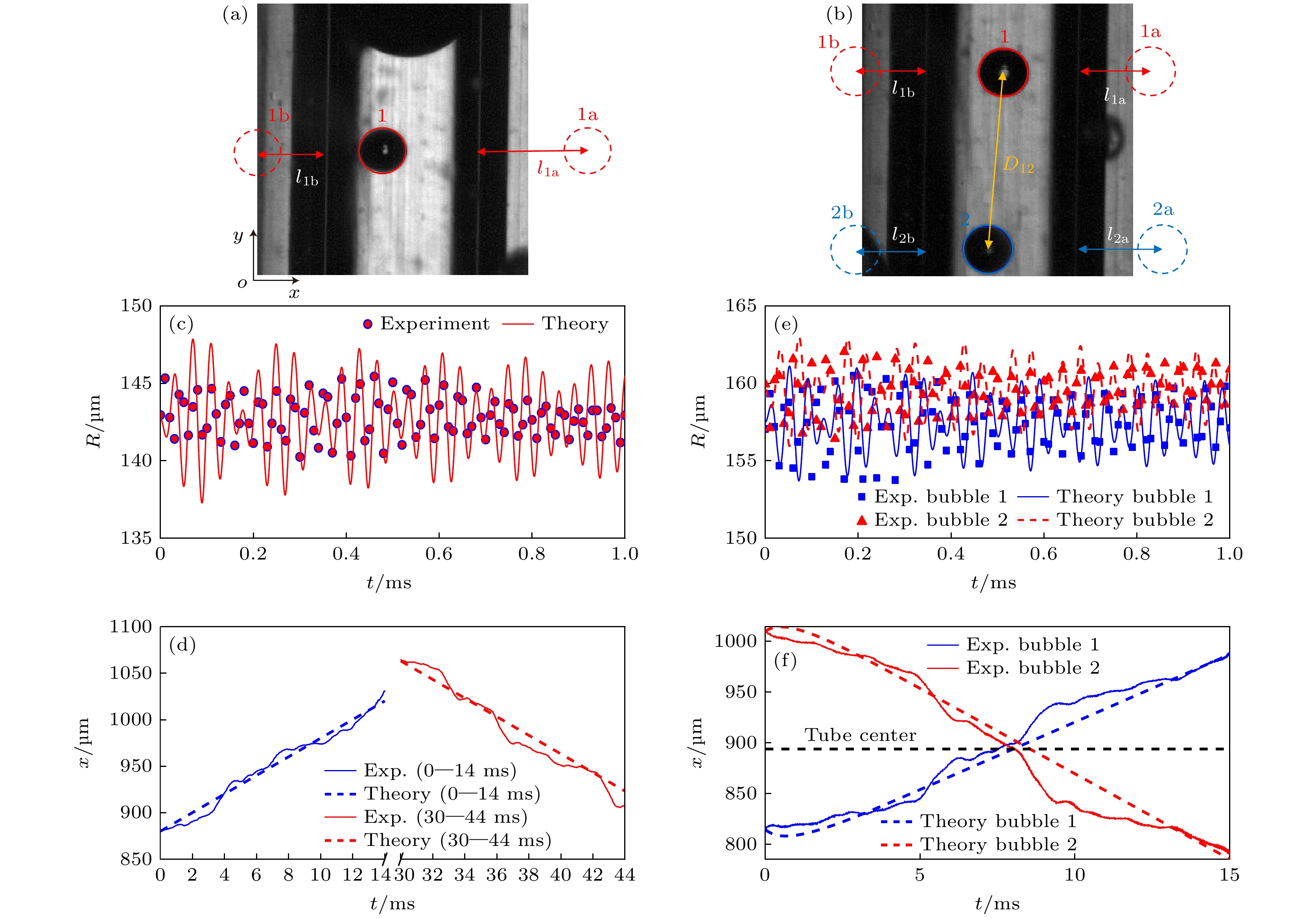
图 13 理论模型与实验对照 (a) 单泡模型图($ {R_{10}} = 142.7 \;{\text{μm}} $, $ {l_{{1 \text{a}}}} = 575.8 \;{\text{μm}} $, $ {l_{{1 \text{b}}}} = 424.2 \;{\text{μm}} $, $ \left( {{x_1}, {y_1}} \right) =\left( 893.9 \;{\text{μm}}, $$ 833.3 \;{\text{μm}} \right) $); (b) 双泡模型图($ {R_{10}} = 157.5 \;{\text{μm}} $, $ {R_{20}} = 159.6 \;{\text{μm}} $, $ {l_{{1 \text{a}}}} = 575.8 \;{\text{μm}}$, $ {l_{{1 \text{b}}}} = 424.2 \;{\text{μm}} $, $ {l_{2{\text{a}}}} = 393.9 \;{\text{μm}} $, $ {l_{{2 \text{b}}}} = $$ 606.1 \;{\text{μm}} $, $ {D_{12}} = 1136.4 \;{\text{μm}} $, $ \left( {{x_1}, {y_1}} \right) = \left( {814.7 \;{\text{μm}}, 1363.6 \;{\text{μm}}} \right) $, $ \left( {{x_2}, {y_2}} \right) = \left( {1009.9 \;{\text{μm}}, 242.4 \;{\text{μm}}} \right) $); (c) 单泡振荡特性; (d) 双泡振荡特性; (e) 单泡平动特性; (f) 双泡平动特性
Figure 13. Comparison between theoretical model and experimental results: (a) Single-bubble model ($ {R_{10}} = 142.7 \;{\text{μm}} $, $ {l_{{1 \text{a}}}} = 575.8 \;{\text{μm}} $, $ {l_{{1 \text{b}}}} = 424.2 \;{\text{μm}} $, $ \left( {{x_1}, {y_1}} \right) = \left( {893.9 \;{\text{μm}}, 833.3 \;{\text{μm}}} \right) $); (b) dual-bubble model ($ {R_{10}} = 157.5 \;{\text{μm}} $, $ {R_{20}} = 159.6 \;{\text{μm}} $, $ {l_{{1 \text{a}}}} = 575.8 \;{\text{μm}} $, $ {l_{{1 \text{b}}}} = 424.2 \;{\text{μm}} $, $ {l_{2{\text{a}}}} = 393.9 \;{\text{μm}} $, $ {l_{{2 \text{b}}}} = 606.1 \;{\text{μm}} $, $ {D_{12}} = 1136.4 \;{\text{μm}} $, $ \left( {{x_1}, {y_1}} \right) = \left( {814.7 \;{\text{μm}}, 1363.6 \;{\text{μm}}} \right) $, $ \left( {{x_2}, {y_2}} \right) = \left( {1009.9 \;{\text{μm}}, 242.4 \;{\text{μm}}} \right) $); (c) single-bubble oscillation characteristics; (d) dual-bubble oscillation characteristics; (e) single-bubble translational behavior; (f) dual-bubble translational behavior.
图 14 泡间距离对共振频率(a)和相位差(b)的影响
Figure 14. Effect of inter-bubble distance on the (a) resonance frequency and (b) phase difference.
图 15 管壁约束对共振频率(a)和相位差(b)的影响
Figure 15. Effect of Wall confinement on the (a) resonance frequency and (b) phase difference.
图 16 两泡间振荡相位差随介质黏度的变化
Figure 16. Variation of oscillation phase difference between two bubbles with medium viscosity.
-
[1] Jiang L L, Xue Z Q, Park H 2019 Int. J. Heat Mass Transf. 138 1211
Google Scholar
[2] Zhai H Y, Xue Z Q, Park H, Aizawa Y, Baba Y, Zhang Y 2020 J. Nat. Gas Sci. Eng. 77 103233
Google Scholar
[3] Chen H, Kreider W, Brayman A A, Bailey M R, Matula T J 2011 Phys. Rev. Lett. 106 034301
Google Scholar
[4] Miller D L, Quddus J 2000 Proc. Natl. Acad. Sci. U. S. A. 97 10179
Google Scholar
[5] Marmottant P, Hilgenfeldt S 2004 Proc. Natl. Acad. Sci. U. S. A. 101 9523
Google Scholar
[6] Liu Y, Zhou Y, Zhang W, Chen S, Liang S 2024 J. Biomed. Eng. 41 919
[7] Sambo C, Liu N, Shaibu R, Ahmed A, Hashish R 2023 Geoenergy Sci. Eng. 221 111185
Google Scholar
[8] Mamba S S, Magniez J C, Zoueshtiagh F, Baudoin M 2018 J. Fluid Mech. 838 165
Google Scholar
[9] Averkiou M A, Bruce M F, Powers J E, Sheeran P S, Burn P N 2020 Ultrasound Med. Biol. 46 498
Google Scholar
[10] Battat S, Weitz D A, Whitesides G M 2022 Chem. Rev. 122 6921
Google Scholar
[11] Rasouli M R, Tabrizian M 2019 Lab Chip 19 3316
Google Scholar
[12] Liao A H, Ho H C, Lin Y C, Chen H K, Wang C H 2015 PLoS One. 10 e0138500
Google Scholar
[13] Minnaert M 1933 Philos. Mag. 16 235
Google Scholar
[14] Plesset M S 1949 J. Appl. Mech. 16 277
Google Scholar
[15] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[16] Qin S, Ferrara K W 2006 Phys. Med. Biol. 51 5065
Google Scholar
[17] Zhong P, Zhou Y F, Zhu S L 2001 Ultrasound Med. Biol. 27 119
Google Scholar
[18] Caskey C F, Stieger S M, Qin S, Dayton P A, Ferrara K W 2007 J. Acoust. Soc. Am. 122 1191
Google Scholar
[19] Zhang L L, Chen W Z 2024 Ultrason. Sonochem. 110 107050
Google Scholar
[20] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[21] Wang C, Lin S 2011 Acta Acust. 36 325
[22] Zilonova E, Solovchuk M, Sheu T W H 2019 Phys. Rev. E 99 023109
Google Scholar
[23] Zou Q Q, Zhong X H, Zhang B Y, Gao A Y, Wang X, Li Z Y, Qin D 2023 Ultrasonics 134 107089
Google Scholar
[24] Fei Y J, Zhu C Y, Fu T T, Gao X Q, Ma Y G 2022 Chin. J. Chem. Eng. 50 66
Google Scholar
[25] Hu M, Wang F, Li Y, Chen L, Wu W, Huo P, Deng D 2025 Phys. Rev. Lett. 134 104004
Google Scholar
[26] Magnaudet J, Legendre D 1998 Phys. Fluids 10 550
Google Scholar
[27] Legendre D, Magnaudet J, Mougin G 2003 J. Fluid Mech. 497 133
Google Scholar
[28] Qi H Y, Liu J T, Sun X Y, Deng P, Zhang D M, Song Y X 2024 Phys. Fluids 36
[29] Alt E, Banyai S, Banyai M, Koppensteiner R 2002 Thromb. Res. 107 101
Google Scholar
[30] Lei Z K, Dong X R, Zuo X Y, Wang C H, Wu Y R, Lin S Y, Guo J Z 2024 J. Acoust. Soc. Am. 156 3373
Google Scholar
[31] Guo C, Wang J, Li X H, Yang S Q, Li W H 2024 Chem. Eng. Process. 199 109765
Google Scholar
[32] Doinikov A A 2001 Phys. Rev. E 64 026301
Google Scholar
[33] Ida M 2009 Phys. Rev. E 79 016307
Google Scholar
[34] Sugita N, Sugiura T 2017 Ultrasonics 74 174
Google Scholar
[35] Regnault G, Doinikov A A, Laloy G, Mauger C, Benon P, Catheline S, Inserra C 2024 Phys. Fluids 36
DownLoad:
Metrics
- Abstract views: 301
- PDF Downloads: 4
- Cited By: 0
