The frontiers and applications of topological physics
编者按：
从凝聚态物理中的电子到经典物理系统中的光波和声波, 按意愿对粒子和波的传输进行调控, 一直是人们孜孜不倦探索和追寻的目标, 其导致了现代半导体和光电子、电声等信息产业的诞生和蓬勃发展. 然而在传统材料中, 由于存在着难以避免的缺陷和杂质, 以及由于加工制造过程引入的粗糙度等, 使得粒子与波在传输过程中产生大量的散射和损耗, 从而引入了大量的噪声和提高了功耗, 极大地制约了相关技术的应用与发展. 因而, 如何减小粒子和波在传输过程中 (特别是长程传输过程中) 的散射和损耗成为当前相关信息领域研究的一项重大挑战.
全新的材料也带来了新的研究问题. 尽管钙钛矿材料的光电性能优异、进展迅速, 人们发现这类材料目前并不是完美的. 钙钛矿材料的稳定性问题给领域内研究者带来了新的挑战; 铅元素毒性问题的解决也依赖于研究者在非铅钙钛矿领域的突破; 蓝光钙钛矿 LED 较差的性能也给实现全彩钙钛矿显示的愿景蒙上了阴影. 此外, 钙钛矿中的多种物理机制目前仍不明确, 处于激烈的争论当中. 种种问题都有待于领域内研究者的充分探讨.
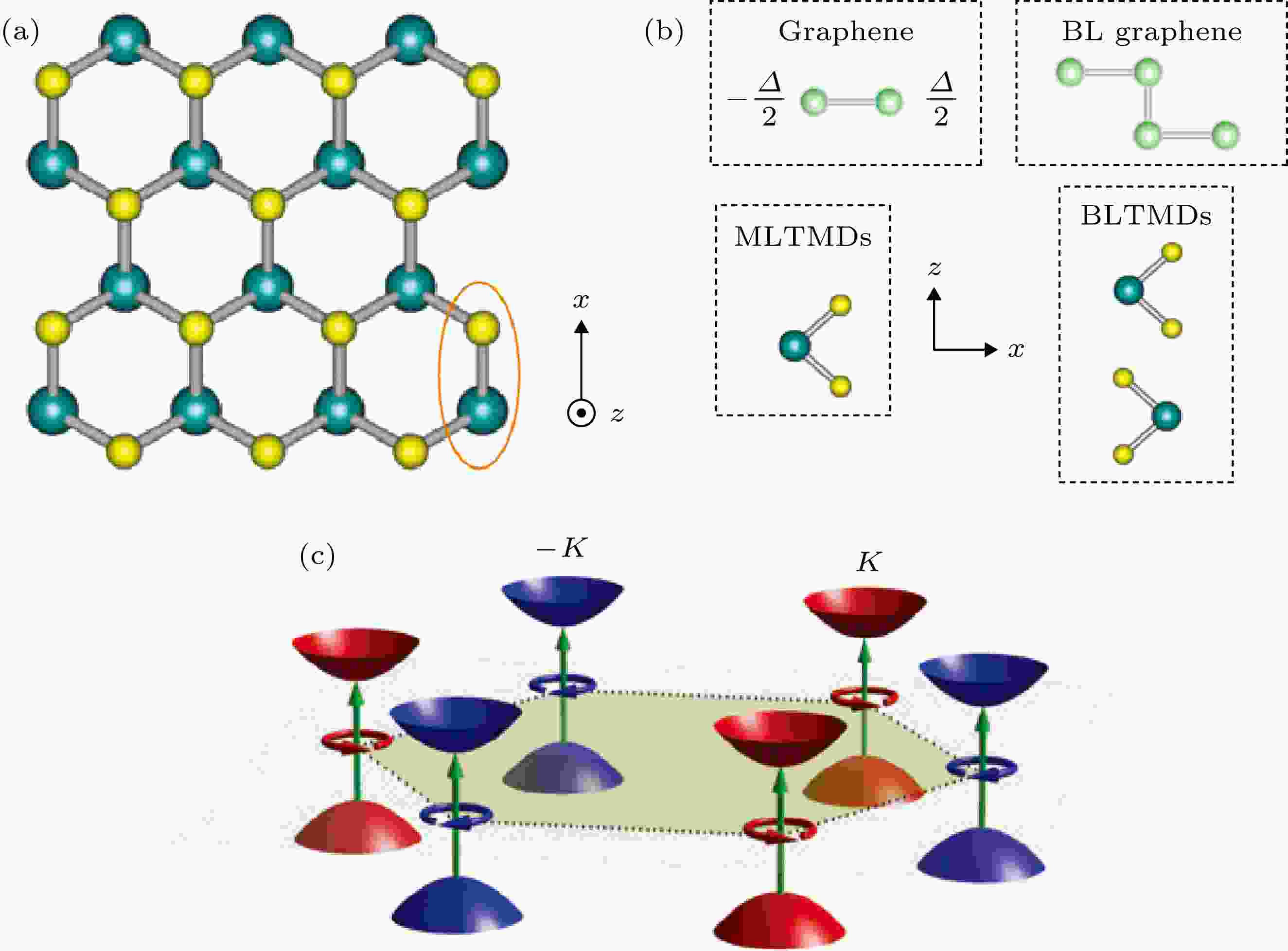
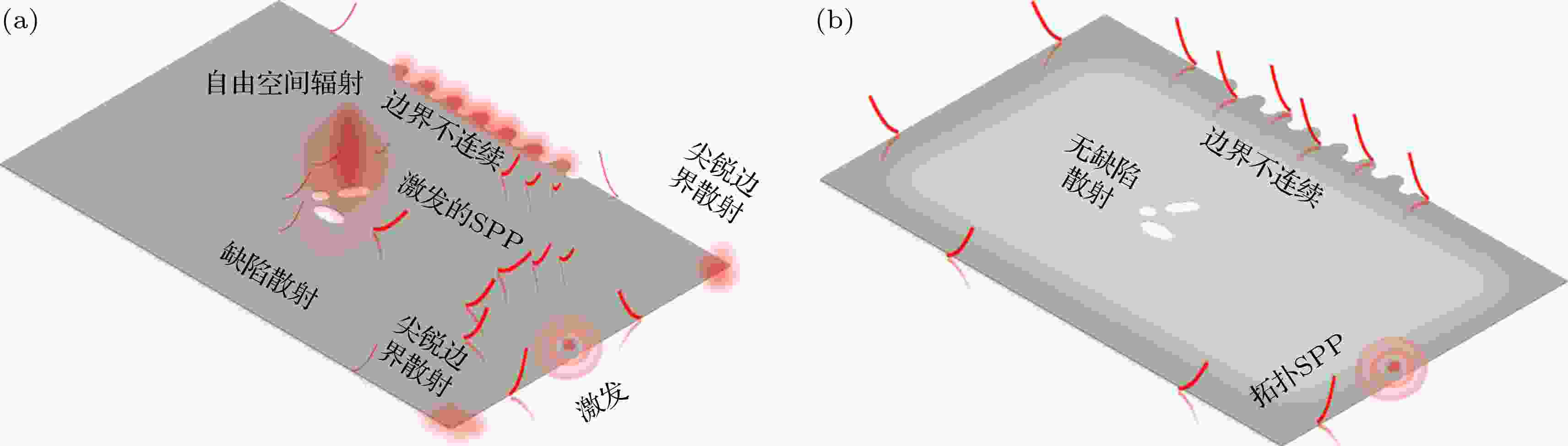
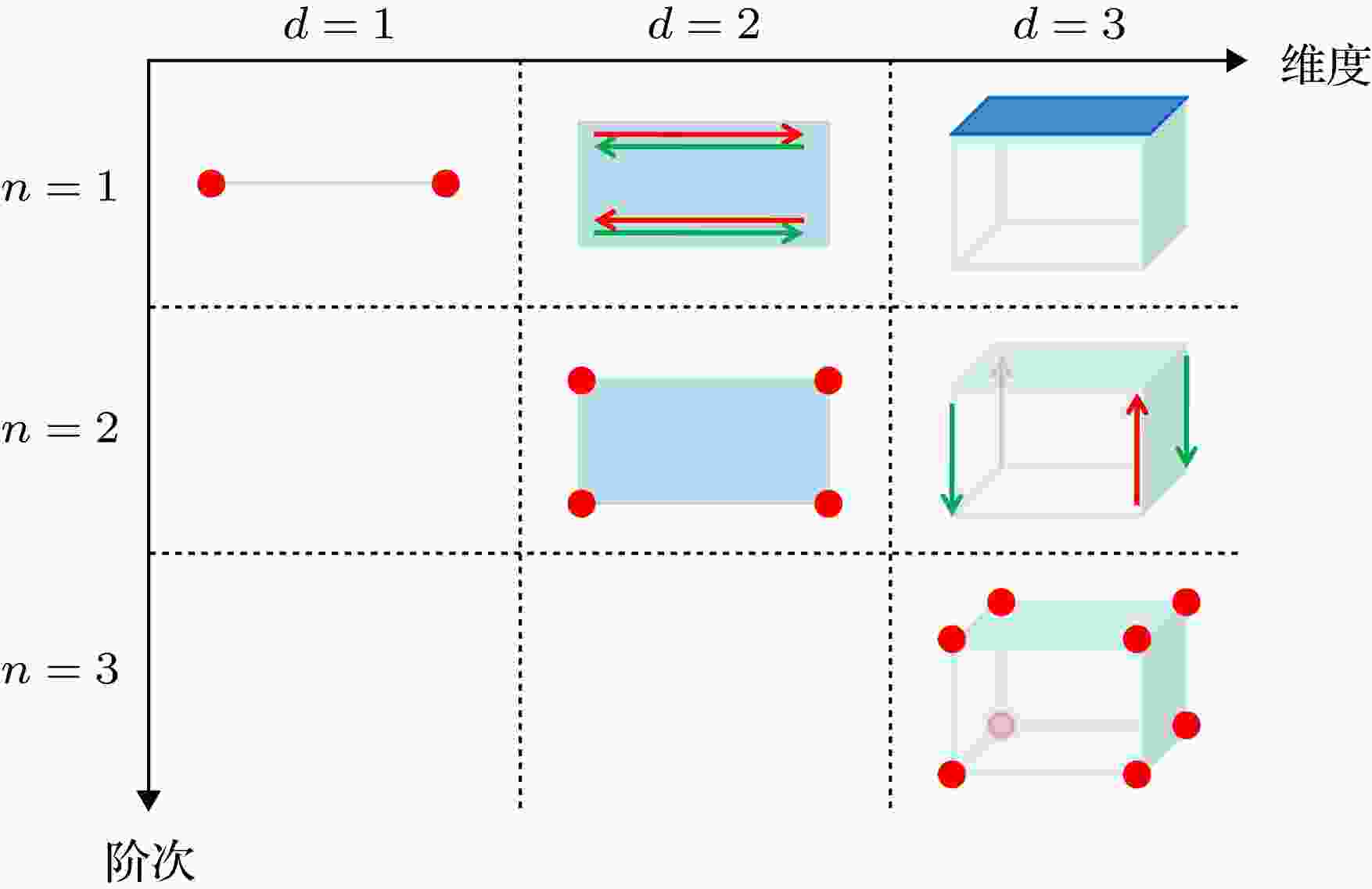
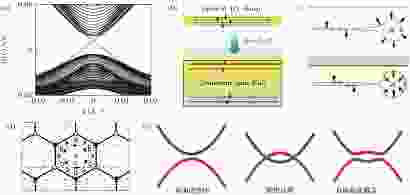
拓扑材料的出现, 则为克服这一挑战提供了巨大的机遇. 从上世纪八十年代开始, 在凝聚态领域中, 人们发现一类新奇的物质相变过程,诸如 KT 相变和量子霍尔效应, 其并不满足刻画经典相变现象的对称性自发破缺理论, 甚至没有局域的序参量. 事实证明, 这些特殊的物质相变可以从量子态的拓扑结构出发去解释. 对这类相变的研究和探索, 促使了拓扑物理和拓扑材料的诞生和发展. 拓扑物理作为凝聚态领域一个新兴的研究方向, 其不仅在理论上具有诸如体边对应关系, 维度层级现象和手征反常等深刻的物理内涵, 而且存在着受拓扑保护的、无损耗和能够克服缺陷散射的边界传播态以及新奇的体输运现象. 这些新的物理效应, 为人们设计和实现突破传统技术极限的颠覆性材料打下了深刻的科学基础, 从而在光、声、电等领域有着重大应用前景. 在电子材料方面, 具有带隙的拓扑绝缘体能够实现对缺陷免疫的电荷和自旋流；而拓扑超导体中存在的受拓扑保护的马约拉纳零能模式则是实现拓扑量子计算的基础. 在光子晶体、声子晶体等人工带隙材料中, 拓扑物理也促使了诸如单向传播光、声波导, 自旋选择的能量分束器, 光、声隔离器, 拓扑激光, 拓扑路由器新型器件的设计和发明. 相比于电子材料, 人工带隙材料由于其能带结构不受费米能级的约束, 加之其灵活多变的结构可调可控性、高精度的材料加工工艺以及宏观精细测量的优越性等, 从而成为实验观测和实际应用拓扑物理的理想平台, 吸引着人们的广泛关注.
当前, 在拓扑物理领域的研究中, 国际竞争异常激烈, 国内学者也在其中占据一席之地. 为了帮助读者们迅速和系统地了解这一领域的前沿发展, 《物理学报》组织了这期有关拓扑物理前沿与应用的专题, 邀请了部分国内活跃在这一领域的专家学者, 从电子材料、光子晶体、声子晶体、等离激元、电路系统等材料平台到理论、实验和测量手段等诸多方面, 以不同的视角综合叙述了这一领域的研究现状、前沿进展、关键问题和未来展望. 希望本专题的文章能够为国内拓扑物理领域研究的学术交流做一些微薄的贡献, 进一步促进该研究领域的发展.
2019, 68 (22): 220302.
doi: 10.7498/aps.68.20191463
Abstract +
Phonon is a quasi-particle excitation after the second quantization of lattice vibration. In the phonon framework, we can describe mechanics, elastic wave and thermal phenomena in solid uniformly. With the development of our understanding about solid state systems, phonon has become an important method to control device in solid state, which can be seen as a supplement and replacement for electronics and photonics. Among them, the modulation of elastic wave and heat conduction in phonon system has great theoretical and practical value. Elastic wave as an information carrier has the potential to construct new chip elements, while manipulating thermal phonon as an energy carrier can achieve the goal of energy transformation and device optimization. These fields have developed rapidly in recent years. A large number of novel materials such as thermal diodes, elastic meta-materials, thermal meta-materials, and heat pumping devices have been predicted and obtained. These developments are inseparable from the application of the concept of "topology" to phonon systems and the realization of non-reciprocal devices on various scales. In this paper, the topological and nonreciprocal phenomena in phonon systems are tentatively summarized. Besides, the latest research results are introduced and the development trend is prospected. The non-reciprocity of elastic wave and heat flow realized by time-dependent driving is reviewed with emphasis. This method has a great flexibility and can be similarly applied to multi-component systems on all scales.
2019, 68 (22): 220303.
doi: 10.7498/aps.68.20191317
Abstract +
When 2D materials with different lattice constants or lattice rotation angles are stacked together, a periodic moiré pattern will appear. Such moiré superlattice introduces a new two dimensional periodic potential, which can greatly change the physical properties of the original systems. Recent experimental studies of moiré superlattices formed by graphene on graphene and graphene on hexagonal boron nitride have revealed very rich strong correlation effects and topological effects due to novel states in superlattice minibands. It has been shown that flat bands in graphene-based moiré superlattice systems can host both topological states and strongly correlated states, which can be controlled by an external electric field. In bilayer graphene, ABC stacked trilayer graphene and twisted bilayer-bilayer graphene, the number of valence and conduction bands near the Dirac point and even the band topology and bandwidth can be changed by varying the stacking angle between graphene layers or the applied bias voltage. Moreover, the competition between kinetic energy and coulomb interaction depends on the bandwidth and the external electric field, and at the so-called magic angle mott insulator states and superconductivity were observed. Twisted bilayer-bilayer graphene has also been predicted to show similar intriguing properties, including electrically tunable strongly correlated insulators, superconductivity and many rich topological states. In graphene-based moiré systems, the combination of topological states and strong correlations is expected to lead to a broad range of novel phenomena that are not achievable in other material systems. Therefore, graphene moiré systems is likely to bring substantial progress to the study of topological materials. In this paper, we review theoretical and experimental investigations of the topological properties of graphene moiré superlattices, including topological domain wall states in bilayer graphene and topological effects in twisted bilayer graphene, ABC trilayer graphene and twisted double bilayer graphene. The origins of topological properties of these systems are discussed as well as topological phenomena observed in various experiments. Finally, recent near-field optical studies of the band structure and novel topological properties of graphene moiré superlattices are discussed.
2019, 68 (22): 220304.
doi: 10.7498/aps.68.20191410
Abstract +
In this review, we give a brief review on the recent progress in the theoretical research of quench dynamics in topological band systems. Beginning with two band models, we introduce conception of dynamical Chern number and give the connection between the dynamical Chern number and topological invariant in the corresponding equilibrium systems. Then by studying the 1 + 1 dimensional parent Hamiltonian, we show the complete dynamical classification of Altland-Zirnbauer classes, and show the crossing of entanglement spectrum as a feature of dynamical bulk edge correspondence. Furthermore, we consider the impact of the disorder and band dispersion. At last, we show the experimental simulation of dynamical Chern number by a superconducting qubit system.
2019, 68 (22): 220305.
doi: 10.7498/aps.68.20191398
Abstract +
Based on the correspondence between tight-binding Hamiltonian in condensed matter physics and the Kirchhoff’s current equations in lumped parameters circuits, profuse topological states can be mapped from the former to the latter. In this article, the electric-circuit realizations of 1D SSH model, 3D nodal-line and Weyl semimetals are devised and elaborated, in which the edge states, surface drum-head and Fermi-arc states are appearing on the surface of the circuit lattice. Of these circuits, the effective hopping terms in Hamiltonian have high degree of freedom. The hopping strength, distance and dimension are easy to tune, and therefore our design is convenient to be extended to non-Hermitian and four or higher dimensional cases, making the fancy states that hard to reach in conventional condensed matter now at our fingertips. Besides, the electric circuit has the advantage of plentiful functional elements and mature manufacture techniques, thus being a promising platform to explore exotic states of matter.
2019, 68 (22): 224101.
doi: 10.7498/aps.68.20191085
Abstract +
The miniaturization of electromagnetic devices is a long-term theme for the development of modern technologies to achieve higher flexibilities, better performances, and higher density integration. Surface plasmon polaritons (SPPs) provide a powerful solution for reducing the size of integrated electromagnetic device due to its deep subwavelength confinement. However, materials or structures that support SPPs inevitably have impurities or structural defects, which leads to the loss of the propagating mode. In order to avoid scattering from impurities or defects, topological structures are introduced to address issues of discontinuities and have been proved to be an effective solution. In this paper, we first review the recent efforts devoted to SPPs based optical devices and those of artificial surface plasmon in terahertz/microwave band, and then summarize several important topological systems of SPPs. Finally, we present our perspectives on the future developments of this field.
2019, 68 (22): 224206.
doi: 10.7498/aps.68.20191437
Abstract +
Inspired by topological phases and phase transitions in condensed matter, a new research field based on topological band theory, topological photonics, has emerged. It breaks through the traditional idea of light regulation by optical superposition principle of real space and energy band theory of solids of reciprocal space, providing a novel mechanism of optical regulation and rich properties of transport and light manipulation. Such as transmission properties of against backscattering and rubout to defects and disorders, selective transports dependent on spin-orbit coupling, and high dimensional manipulation of light. This review paper classifies different topological photonic systems by dimensions, briefly introducing the topological model, the novel physical phenomena, and the corresponding physical picture, such as SSH models, photonic quantum Hall effects, photonic quantum spin Hall effects, photonic Floquet topological insulator, and photonic three-dimensional topological insulator; other advanced platforms such as higher-order, non-Hermitian, and nonlinear topological platforms are also involved; a summary and outlook about the current development, advantages, and challenges of this field are present in the end.
2019, 68 (22): 224301.
doi: 10.7498/aps.68.20190951
Abstract +
Based on honeycomb-lattice sonic crystals with gear-like scatterers, we study and design a pseudospin-dependent dual-band acoustic topological insulator. Compared with cylindrical scatterers with only a single tunable structure parameter (radius), there exist four tunable parameters for the gear scatterer, which enables the sonic crystal to realize four-fold accidental degeneracy at two different frequencies simultaneously. By changing structure parameters of the gear-like scatterers, we can obtain topological phase transitions between two sonic crystals. Based on this, we design acoustic topological waveguides based on two honeycomb-lattice sonic crystals with different topological phases, and introduce two kinds of defects (a lattice disorder and a bend) into the topological waveguide near the domain wall. Numerical simulations show that pseudospin edge states almost immune to two types of defects and can pass through the topological waveguides with negligible backscatterings. Compared with the results for the topological waveguide without defects, the measured transmission spectra are almost unchanged with the two types of defects, which further experimentally verify the robustness of pseudospin-dependent edge states. Additionally, by keeping the structure of the sonic crystals unchanged, we can also obtain another four-fold accidental degenerate Dirac point and the corresponding topological sound phase transitions in the high-frequency region. The simulations show that there also exists a pair of edge states in the overlapped bulk bandgap of the two sonic crystals in the high-frequency region. It is worth noting that the tiny gap between two edge states is larger than that in the low-frequency region, which may arise from the greater difference between the distributions of pressure eigenfunction of two sonic crystals. The proposed dual-band acoustic topology insulator has potential applications in multi-band sound communication and sound information processing.
2019, 68 (22): 226101.
doi: 10.7498/aps.68.20191101
Abstract +
2019, 68 (22): 226801.
doi: 10.7498/aps.68.20191631
Abstract +
Topological state is a rapidly emerging branch of condensed matter physics in recent years, among which two-dimensional topological insulators (2D TIs) have attracted wide attentions due to their great potential in basic research and applications. The 2D TI has insulating bulk state and conductive edge state. Its edge state is protected by time inversion symmetry and will not be backscattered by weak disordered impurities on the boundaries, thus forming a dissipationless edge conductive channel. Compared with 3D TIs, the edge state of 2D TIs can only propagate in two directions, meaning stronger anti-interference with robustness, thus is of great significance for the development of advanced integrated circuits with low energy consumption. Among many experimental methods for studying two-dimensional materials, scanning tunneling microscopy is a surface-sensitive tool with high atomic and energy resolution to locally detect the electronic structure of the material surface. By detecting the edge state of 2D materials in real space, it is particularly suitable for characterizing their topological properties. This paper traces the research progress of 2D TIs, and illustrates their spectroscopic evidences to resolve the nontrivial properties of the one-dimensional edge states. Combined with theoretical calculations, the topological edge states are verified to reside within the bulk energy gap, as well as being localized in the vicinity of step boundaries with a specific spatial distribution in real space. Finally, we discuss the tunability and manipulations of 2D topological materials through structural and external fields, which show promising prospects for applications in future spintronics and energy-saving devices.
2019, 68 (22): 227101.
doi: 10.7498/aps.68.20191538
Abstract +
Electronic band crossing can not only form zero-dimensional nodal points, but also one dimensional nodal lines and two dimensional nodal surfaces. These topological band features have been attracting significant research interest, as they may lead to many special physical properties. In this article, we review the progress in this field, including the conceptual development, the character and classification of these nodal structures, and the material realization.
2019, 68 (22): 227102.
doi: 10.7498/aps.68.20191544
Abstract +
Topological semimetal, known as a type of topological quantum materials without energy gap, has attracted lots of research interests due to its unique physical properties such as novel quasiparticles, giant magnetoresistance and large carrier mobility. Topological semimetal can be further classified into topological Dirac semimetal, topological Weyl semimetal, topological nodal-line semimetal and topological semimetals with " new fermions”. The high-resolution angle-resolved photoemission spectroscopy (ARPES) has emerged as a powerful experimental technique to directly visualize the electronic structure and identify the characteristic topological electronic states in topological semimetals. Here we would briefly introduce the ARPES technique and review some of the recent progress of ARPES study on the electronic structures of typical topological semimetals. We would focus mostly on the physics origin and ARPES signature of topological electronic structures and hope the readers would find it interesting and useful in the understanding of this material class which both is important in physics and has promising application potentials.
2019, 68 (22): 227202.
doi: 10.7498/aps.68.20191433
Abstract +
Topological insulators (TIs), with unique bulk insulating and two-dimensional surface conducting states, show great promise of future optospintronics and spintronics applications, where a complete knowledge of the charge and spin dynamics is quite essential. Thus, the non-equilibrium properties inside TIs have attracted enormous attention. Here in this paper, we review the latest achievements in this field. The focus will be mainly on the experimental study, covering the ultrafast dynamical properties of charge, phonon, and spin. We hope that this review can stimulate further studies, especially theoretical research concerning the properties of topological insulators out of thermodynamic equilibrium.
2019, 68 (22): 227203.
doi: 10.7498/aps.68.20191501
Abstract +
Planar Hall effect(PHE) is a newly emerging experimental tool to detect chiral anomaly and nontrivial Berry curvature in topological semimetals, as chiral-anomaly-induced negative magnetoresistance is sensitive to the angle between magnetic field B and current I. Here we demonstrate the PHE in a topological nodal-line semimetal ZrSiSe device by electric transport measurement. According to our analysis, we conclude that the PHE results from the trivial anisotropic magnetoresistance (AMR). We argue that there is no inevitability between PHE and chiral anomaly, and some other mechanisms can induce PHE. This work indicates that PHE cannot be considered as evidence of chiral anomaly and one may seek for non-topological origin in such studies.
2019, 68 (22): 227801.
doi: 10.7498/aps.68.20191098
Abstract +
Plasmonics plays an important role in the development of nanophotonics, which allows breaking diffraction limit and controlling light in deep-subwavelength scale due to the strong interaction between light and free carriers. Noble metals and 2-dimensional electron gas have been the main platforms for studying plasmonics over the past decade. The metal-based plasmonic devices have exhibited great potential in various applications, including integrated photonic systems, biological sensing, super-resolution imaging and surface-enhanced Raman scattering, etc. Because of the high carrier density, plasmons of noble metals are realized in the near-infrared to visible frequency range. With the rapid development of new materials, many other plasmonic materials are discovered to exhibit new properties. One example is the graphene plasmons working in the mid-infrared and terahertz spectral range, which exhibit strong field confinement and frequency tunability due to the massless Dirac fermions and other exotic electrical and optical properties. Recently, topological materials, the band structures of which are composed of cones with linear dispersion like in graphene, are discovered, such as the topological insulators, Dirac semimetals, Weyl semimetals and nodal line semimetals, providing another platform to study the Dirac plasmons. Such linear dispersion results in small electron mass and unique carrier density dependence of plasmons. In addition, topological materials possess a tremendous amount of exotic electron properties, such as the ultrahigh mobility, topological surface states and chiral anomaly in Weyl semimetals, etc. Many of these electronic properties can be inherited by the collective oscillation of free electrons, promising new possibility for plasmonics. Here, the experimental observations of plasmons in topological insulators and topological semimetals are reviewed, with special focus on the studies based on electron energy loss spectrum and Fourier transform infrared spectroscopy. At the end, other topological materials with potential for hosting 2D plasmons are discussed. This review provides an overview of plasmons in topological semimetals and may stimulate further quest of more exotic features for plasmons.
2019, 68 (22): 227802.
doi: 10.7498/aps.68.20191007
Abstract +
2019, 68 (22): 227803.
doi: 10.7498/aps.68.20191452
Abstract +
Topology photonic, a combination of topology physics and optics provides novel visions to the demonstration of theoretical physics and designs principles to new optical devices. Being a key tool to condensed matter physics, tight-binding model helps the development of topology physics. We found that by changing the background material from vacuum to an effective medium with negative permittivity in traditional photonic crystals, a one-to-one correspondence to tight-binding model can be found for this new type of photonic crystal. We show by numerical simulations the existence of edge states located at both the zigzag and bearded boundaries of a honeycomb-lattice photonic crystal imbedded in negative permittivity material. Two experimental realizations are proposed that it is possible to build up a demonstration platform working at microwave frequencies to verify corresponding topology physics theories using simple photonic crystal structures. We hope that the successful verification of new topology physics can further trigger applications in optics.
2019, 68 (22): 227804.
doi: 10.7498/aps.68.20191510
Abstract +
Topological semimetal represents a novel quantum phase of matter, which exhibits a variety of fascinating quantum phenomena. This class of materials not only have potential applications in electronic devices, but also represent one of the hottest topics in the field of quantum materials. According to the band structure of these materials in the three-dimensional momentum space, topological semimetals can be classified into Dirac semimetals, Weyl semimetals and nodal-line semimetals. Extensive studies on these materials have been conducted using various techniques. For example, angle-resolved photoemission spectroscopy (ARPES) has directly observed the Fermi arc that connects two Weyl points with opposite chiralities in the surface states of Weyl semimetals; the Dirac points, Weyl points as well as the Dirac nodal line in the bulk states have also been revealed by soft X-ray ARPES; the observation of negative magnetoresistance in transport measurements has been taken as the evidence for the chiral anomaly in Weyl and Dirac semimetals; the chirality of the Weyl fermions have been detected by measuring the photocurrent in response of circularly polarized light; in addition, strong second harmonic generation and THz emission have been observed, indicating strong non-linear effects of Weyl semimetals. Infrared spectroscopy is a bulk-sensitive technique, which not only covers a very broad energy range (meV to several eV), but also has very high energy resolution (dozens of µeV). Investigations into the optical response of these materials not only help understand the physics of the topological phase and explore novel quantum phenomena, but also pave the way for future studies and applications in optics. In this article, we introduce the optical studies on several topological semimetals, including Dirac, Weyl and nodal-line semimetals.
2019, 68 (22): 227805.
doi: 10.7498/aps.68.20191363
Abstract +
The manipulation of surface acoustic wave (SAW) in phononic crystal plays an important role in the applications of SAW. The introduction of topological acoustic theory has opened a new field for SAW in phononic crystals. Here we construct pseudospin modes of SAW and topological phase transition along the surface of phononic crystal. The local SAW propagation is realized by air cylindrical holes in honeycomb lattice arranged on rigid substrate, and the Dirac cone is formed at the K point of the first Brillouin zone. Furthermore, using the band-folding theory, double Dirac cones can be formed at the center Гs point in the Brillouin zone of compound cell that contains six adjacent cylindrical air holes. The double Dirac cone can be broken to form two degenerated states and complete band gap by only shrinking or expanding the spacing of adjacent holes in the compound cell. It is found that the direction of energy is in a clockwise or counterclockwise direction, thus the pseudospin modes of SAW are constructed. The shrinkage-to-expansion of the compound cell leads to band inversion, and the system changes from trivial state to nontrivial state, accompanied by the phase transition. According to the bulk-boundary correspondence, the unidirectional acoustic edge states can be found at the interface between trivial system and nontrivial system. Then we can construct a topologically protected waveguide to realize the unidirectional transmission of surface waves without backscattering. This work provides a new possibility for manipulating the SAW propagating on the surface of phononic crystals and may be useful for making the acoustic functional devices based on SAW.
2019, 68 (22): 227901.
doi: 10.7498/aps.68.20191450
Abstract +
2020, 69 (7): 077102.
doi: 10.7498/aps.69.20200197
Abstract +
In the presence of symmetry-protection, topological invariants of topological phases of matter in free fermion systems, e.g., topological band insulators, can be directly computed via the properties of band structure. Nevertheless, it is usually difficult to extract topological invariants in strongly-correlated topological phases of matter in which band structure is not well-defined. One typical example is the fractional quantum Hall effect whose low-energy physics is governed by Chern-Simons topological gauge theory and Hall conductivity plateaus involve extremely fruitful physics of strong correlation. In this article, we focus on intrinsic topological order (iTO), symmetry-protected topological phases (SPT), and symmetry-enriched topological phases (SET) in boson and spin systems. Through gauge field-theoretical approach, we review some research progress on these topological phases of matter from the aspects of projective construction, low-energy effective theory and topological response theory.
2020, 69 (7): 077303.
doi: 10.7498/aps.69.20200177
Abstract +
Majorana fermions are known for being their own anti-particles. As the condensed matter version of Majorana fermions, Majorana quasiparticles have drawn extensive interests for being an ideal candidate for building a fault-tolerant quantum computer, due to their non-abelian statistics. This paper provides an introduction for beginners to the rapidly growing research field of Majorana quasiparticles focusing on one dimensional semiconductor nanowire-superconductor hybrid system. We aim to help readers to quickly understand Majorana quasiparticles and its formation mechanism and the latest experimental results. We first review the theoretical model of the Majorana quasiparticles with its historical background. We then discuss the Kitaev chain and analyze its key elements. We also introduce typical Majorana devices and their corresponding measurement methods. Furthermore, we discuss the observation of robust signatures of Majorana zero modes in recent experiments, with particular attention to tunneling conductance measurements. Finally, we give prospects on future experiments for advancing one dimensional semiconductor nanowire-superconductor hybrid system.
2020, 69 (7): 077801.
doi: 10.7498/aps.69.20191816
Abstract +
We employ the time resolved pump probe experiment to investigate the ultrafast dynamics in a topological semimetal molybdenum phosphide (MoP), which exhibits triple degenerate points in the momentum space. Two relaxation processes with the lifetime of 0.3 and 150 ps have been observed. We attribute the fast component to the electron-phonon scattering and the slow component to the phonon-phonon scattering, respectively. Temperature dependence investigation shows that both the lifetimes of the fast and slow components enhance slightly with increasing temperature. We also successfully generate and detect a thermal-stress-induced coherent acoustic phonon mode with a frequency of 0.033 THz, which does not vary with temperature. Our ultrafast spectroscopy investigation of the quasiparticle dynamics and the coherent phonon in MoP provides useful experimental facts and information about the overall excited state dynamics and the temperature dependence of electron-phonon coupling.
2020, 69 (14): 147301.
doi: 10.7498/aps.69.20200506
Abstract +
We review and discuss the electronic structures, topological properties and orbital magnetism in twisted bilayer (TBG) and multilayer graphene systems. Moiré pattern is formed in twisted bilayer graphene due to the mutual twist of the two graphene layers. The moiré potential induced by the twist can generate opposite pseudo magnetic fields in the Moiré supercell, which are coupled with the Dirac fermions and generate two sets of pseudo Landau levels with opposite Chern numbers $\pm1$ . The two flat bands for each valley each spin of TBG are equivalent to the two zeroth pseudo Landau levels with opposite Chern numbers and opposite sublattice polarizations. Such a pseudo-Landau-level representation has significant implications on the quantum anomalous Hall states observed at integer fillings of the flat bands in TBG at the magic angle. The origin of the magic angle can also be naturally explained by using the pseudo-Landau-level picture. We further discuss twisted multilayer graphene systems, and show that topological flat bands generally exist in the twisted multilayer graphene systems. These topological flat bands have nonzero valley Chern numbers, which can be described by a succinct formula under certain approxmations. These topological flat bands in twisted bilayer and multilayer graphene systems are associated with orbital magnetism. A valley polarized state in the twist graphene system is an orbital magnetic state with nontrivial current-loop pattern in the moiré supercell. The experimentally observed correlated insulating states at $\pm 1/2$ fillings and at charge neutrality point of magic-angle TBG can be valley polarized states, which are associated with compensating current loops and induce staggered orbital magnetizations on the moiré length scale. If $C_{2z}$ symmetry is broken due to the alignment of hexagonal boron nitride substrate, then a valley-polarized ground state would be a moiré orbital ferromagnetic state, which exhibits not only (quantum) anomalous Hall effect, but also novel magneto-optical and nonlinear optical responses.
