-
Traditional Monte Carlo simulation requires a large number of samples to be employed for calculating various physical parameters, which needs much time and computer resources due to inefficient statistical cases rather than mining data features for each example. Here, we introduce a technique for digging information characteristics to study the phase transition of polymer generated by Monte Carlo method. Convolutional neural network (CNN) and fully connected neural network (FCN) are performed to study the critical adsorption phase transition of polymer adsorbed on the homogeneous cover and stripe surface. The data set (conformations of the polymer) is generated by the Monte Carlo method, the annealing algorithm (including 48 temperatures ranging from T = 8.0 to T = 0.05) and the Metropolis sampling method, which is marked by the state labeling method and the temperature labeling method and used for training and testing of the CNN and the FCN. The CNN and the FCN network can not only recognize the desorption state and adsorption state of the polymer on the homogeneous surface (the critical phase transition temperature TC = 1.5, which is close to the critical phase transition temperature TC = 1.625 of the infinite chain length of polymer adsorbed on the homogeneous surface regardless of the size effect), but also recognize the desorption state, the single-stripe adsorption state and the multi-stripe adsorption state of polymer on the stripe surface(the critical phase transition temperature T1 = 0.55 and T2 = 1.1, which are consistent respectively with T1 = 0.58 and T2 = 1.05 of polymer adsorbed on the stripe-patterned surface derived from existing research results). We obtain almost the same critical adsorption temperature by two different labeling methods. Through the study of the relationship between the size of the training set and the recognition rate of the neural network, it is found that the deep neural network can well recognize the conformational state of polymer on homogeneous surface and stripe surface of a small set of training samples (when the number of samples at each temperature is greater than 24, the recognition rate of the polymer is larger than 95.5%). Therefore, the deep neural network provides a new calculation method for polymer simulation research with the Monte Carlo method.
-
Keywords:
- deep neural network /
- adsorption phase transition /
- polymer /
- Monte Carlo method
[1] Wei Q, Melko R G, Chen J Z Y 2017 Phys. Rev. E 95 032504
[2] Carrasquilla J, Melko R G 2017 Nat. Phys. 13 431
Google Scholar
[3] 邢雪, 于德新, 田秀娟 2017 物理学报 66 230501
Google Scholar
Xing X, Yu D X, Tian X J 2017 Acta Phys. Sin. 66 230501
Google Scholar
[4] Deo R C 2015 Circulation 132 1920
Google Scholar
[5] Lin W Y, Hu Y H, Tsai C F 2012 IEEE. Trans. 42 421
[6] Deng L, Dong Y 2011 Twelfth Annual Conference of the International Speech Communication Association Florence, Italy, August 27–31, 2011 p2285
[7] He K, Zhang X, Ren S 2016 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, USA, June26–July 1, 2016 p770
[8] Sun Q S, Zeng S G, Liu Y 2005 Pattern Recognit. 38 2437
Google Scholar
[9] Porter E W 1989 US Patent 4 829
[10] Jacobs P E, Chang C 1999 US Patent 5 956
[11] Berger A L, Pietra V J D, Pietra S A D 1996 Comput. Linguist. 22 39
[12] Brill E 1995 Comput. Linguist. 21 543
[13] McIlroy G T, Kees J E, Kalscheuer J A 1996 US Patent 5 583
[14] Anneroth G, Batsakis J, Luna M 1987 Eur. J. Oral Sci. 95 229
Google Scholar
[15] Carleo G, Troyer M 2017 Science 355 602
Google Scholar
[16] Ali J B, Fnaiech N, Saidi L 2015 Appl. Acoust. 89 16
Google Scholar
[17] Wang L, Zeng Y, Chen T 2015 Expert Syst. Appl. 42 855
Google Scholar
[18] Vogl T P, Mangis J K, Rigler A K 1988 Biol. Cybern. 59 257
Google Scholar
[19] Li H, Qian C J, Luo M B 2012 J. Appl. Polym. Sci. 124 282
Google Scholar
[20] Li H, Qian C J, Sun L Z 2010 Polym. J. 42 383
Google Scholar
[21] Li H, Qian C J, Wang C 2013 Phys. Rev. E 87 012602
Google Scholar
[22] Li H, Gong B, Qian C J 2013 Sens. Transducers J. 159 242
[23] Luo M B 2008 J. Chem. Phys. 128 044912
Google Scholar
[24] Luo M B, Huang J H 2003 J. Chem. Phys. 119 2439
Google Scholar
[25] Luo M, Huang J, Chen Y 2001 Eur. Polym. J. 37 1587
Google Scholar
[26] Chib S, Greenberg E 1995 Am. Stat. 49 327
[27] Haario H, Saksman E, Tamminen J 2001 Bernoulli 7 223
Google Scholar
[28] Hanley J A, McNeil B J 1982 Radiology 143 29
Google Scholar
[29] Bradley A P 1997 Pattern. Recognit. 30 1145
Google Scholar
[30] Li H, Gong B, Qian C J, Luo M B 2015 Soft Matter 11 3222
Google Scholar
-
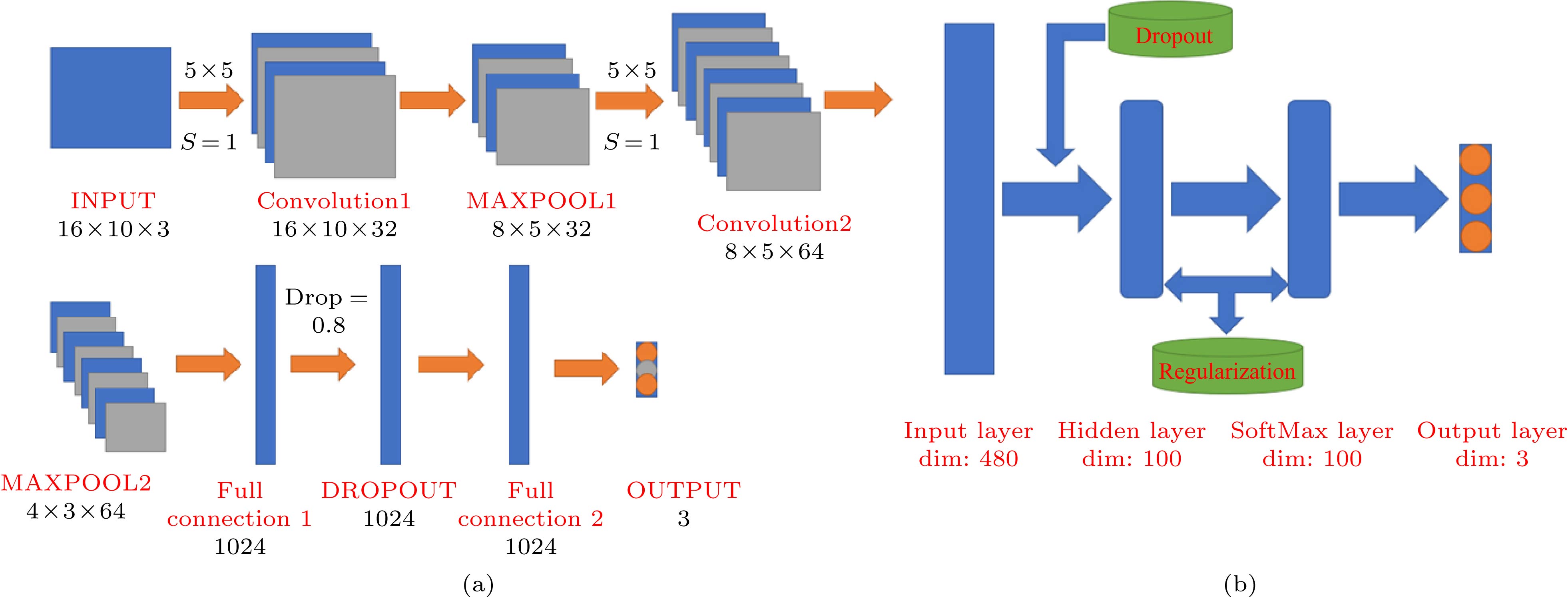
图 1 神经网络结构示意图 (a) 卷积神经网络, INPUT表示输入层, Convolution表示卷积层, MAXPOOL表示池化层, Full connection表示全连接层, OUTPUT表示输出层, PADDING方式均为SAME; (b) 全连接网络的一般结构, 其中hidden layer表示隐藏层, 使用正则化和dropout来防止过拟合, DIM表示输入张量的维度
Figure 1. Schematic diagram of the neural network structure: (a) Convolutional neural network, INPUT is the data entry, OUTPUT is the learning result, and the padding way is SAME; (b) the general structure of a full-connected network, where regularization and dropout are used to prevent overfitting, and DIM represents the dimension of the tensor.
图 2 吸附率与温度之间的关系. 其中链长N = 160, 插图(a) 是温度T = 1.0时的吸附态构象, 插图(b) 是温度T = 2.0时的脱附态构象
Figure 2. Relationship between adsorption rate and temperature. Wherein the chain length N = 160, inset (a) is the conformation of polymer adsorbed on the surface at temperature T = 1.0, and inset (b) is the conformation of polymer desorbed from surface at temperature T = 2.0.
图 3 识别率与训练样本的Epoch, 神经网络层数以及每个温度采用的训练样本数之间的关系 (a) 识别率与Epoch的关系图, SPT (sample per temperature)表示在每个温度下抽取的用于训练神经网络的样本数目, 采用状态标记法标记样本. 其中nh = 1表示隐藏层数目为1, 其他的类似, nh = 1至 nh = 3均采用SPT = 192的样本用于训练, 剩余的样本用于测试与验证, 插图描述的是识别率与隐藏层数目nh的关系, 该识别率为每个学习器最终稳定的识别结果; (b) 识别率与每个温度采用训练样本数目的关系图, 采用状态标记法标记样本, 隐藏层数等于3, 纵坐标为不同训练样本在足够Epoch下达到稳定时的识别率, 测试集均为SPT = 7680, 且与训练集不重复
Figure 3. The relationship between the recognition rate and the Epochs of training case, the number of neural network layers and the number of training samples obtained from each temperature: (a) the plot of recognition rate versus Epochs. SPT (sample per temperature) represents the number of samples extracted at each temperature for training the neural network. The sample is labeled by status. Where nh
= 1 indicates that the number of hidden layers is equal to 1, and the others are similar. All of nh = 1 to 3 uses a sample of SPT = 192 for training, and the remaining samples are used for verification. The illustration depicts the relationship between the recognition rate and the number of hidden layers, which is the final stable recognition result for each classifier; (b) the plot of the recognition rate versus the number of training samples selected at each temperature. The sample is marked by status and the number of hidden layers is equal to 3. The y-axis is the stable recognition rate of different number of training samples under a sufficiently large Epoch. The validation set is SPT = 7680 and is not repeated with the training set. 
图 4 神经网络训练的识别结果图. 横坐标为温度, State表示每个温度下的样本被识别为某个状态的概率, S表示状态标记法, T表示温度标记法, AD表示吸附态, DE表示脱附态. 图为两种标记方法的识别结果, 卷积网络的识别率为98.3%, AUC值为0.9989, 全连接网络为97.6%, AUC值为0.9982, 两种标记方法的临界相变温度
${T_{\rm{C}}} = 1.5$ Figure 4. A plot of the result based on the neural network. The x-axis is the temperature, State represents the probability that the sample at each temperature is recognized as a certain state, The letter S represents the state labeling method, the letter T represents the temperature labeling method, AD represents the adsorption state, and DE represents the desorption state. The figure shows the learning results of the two labeling methods. The recognition rate of the convolutional network is 98.3%, the AUC value is 0.9989, the fully connected network is 97.6%, the AUC value is 0.9982, and the critical phase transition temperature is 1.5 of the two labeling methods.
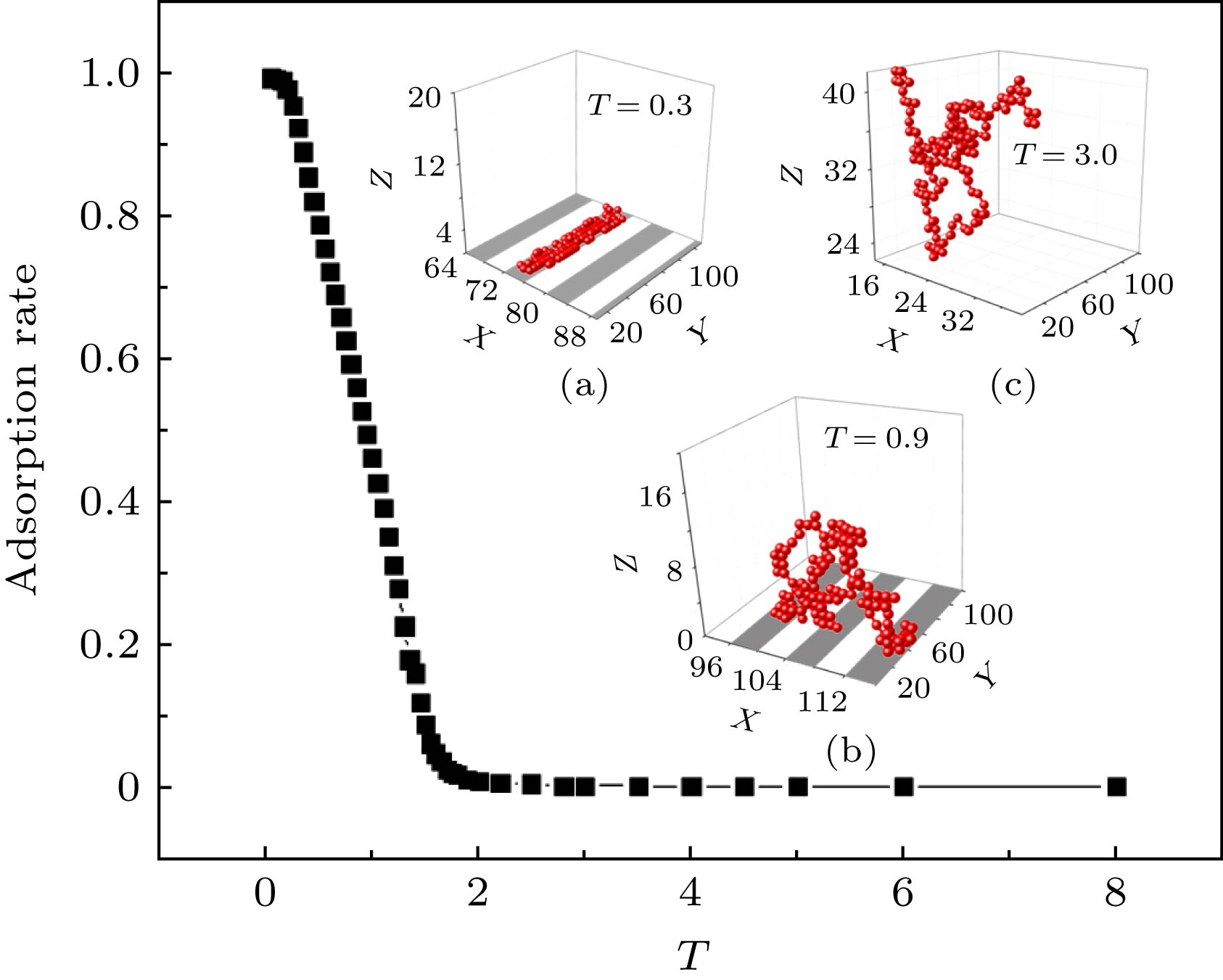
图 5 高分子链在条纹表面的吸附率随温度的变化以及典型的三态构象示意图 (a) 单条纹吸附状态, 温度T = 0.3; (b) 多条纹吸附状态, T = 0.9; (c) 脱附状态, T = 3.0. 其中链长N = 160, 条纹宽度L = 4, 条纹方向垂直于x轴, 沿着y轴方向延伸, 选取的空间尺寸为
$25 \times 120 \times 20$ , 在条纹表面上, 深色部分为吸附条纹, 白色部分为作用力排斥条纹Figure 5. The schematic diagram of the adsorption rate of polymer adsorbed on the stripe surface changes with temperature and typical tri-state conformations: (a) the single-strip adsorption state, where the temperature is 0.3; (b) the multi-strip adsorption state, where the temperature is 0.9; (c) the desorption state, where the temperature is 3.0. Wherein the chain length N is 160, and the stripe width L of the adsorption surface is 4. The stripe direction is perpendicular to the x axis and extends along the y axis, and the selected space size is
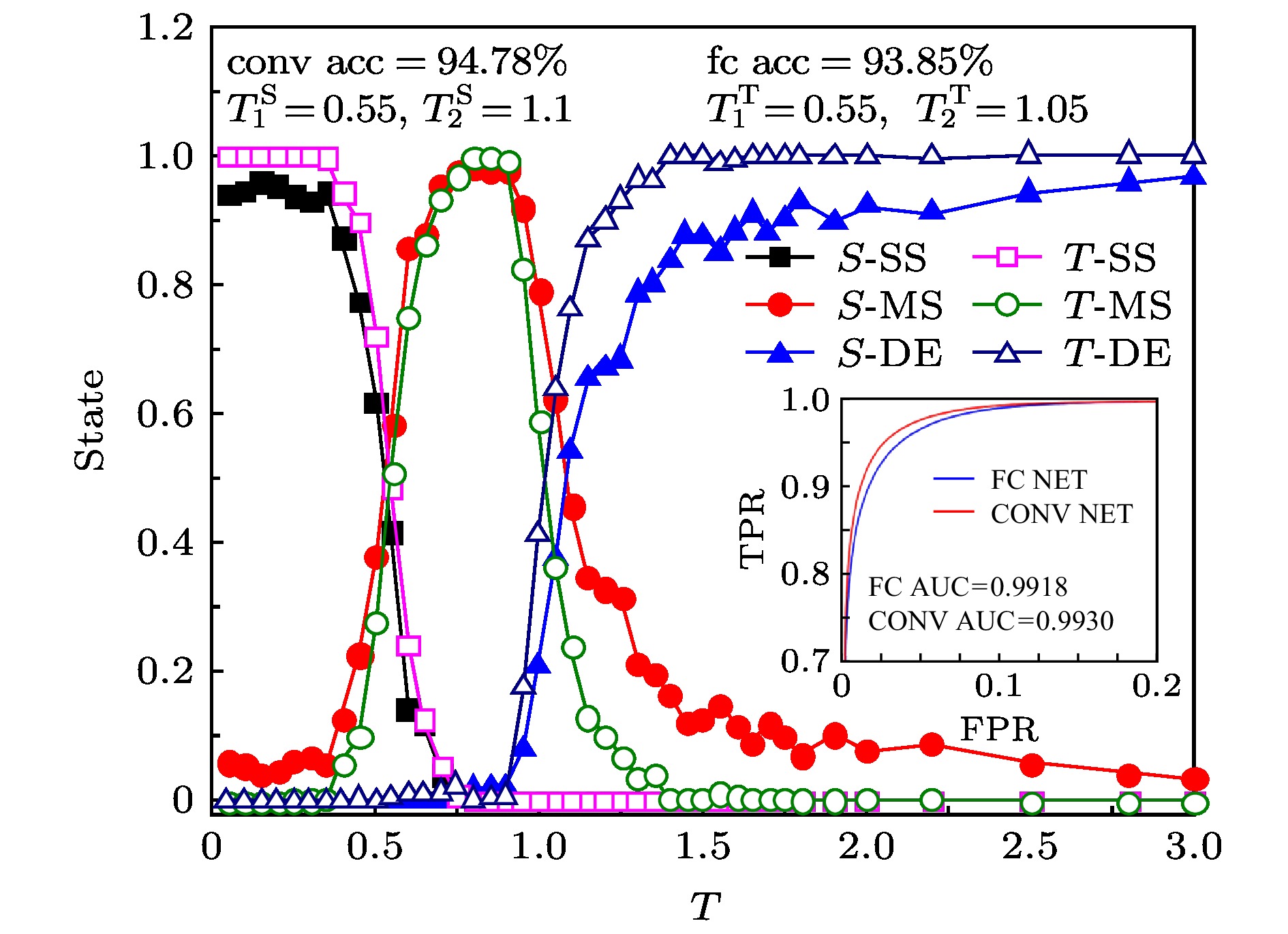
$25 \times 120 \times 20$ . For the adsorption surface, the dark part is the adsorption surface and the white part is the non-force surface.
图 6 神经网络训练的识别结果图 横坐标为温度, 纵坐标State表示每个温度下的样本被识别为某个状态的概率, 图标中S表示状态标记法, T表示温度标记法, SS表示单条纹吸附态, MS表示多条纹吸附态, DE表示脱附态. 其中卷积网络的识别率为94.78%, AUC值为0.9930, 全连接网络为93.85%, AUC值为0.9918, 状态标记法的临界相变温度
${T_1} = 0.55$ ,${T_2} = 1.1,$ 温度标记法的临界相变温度${T_1} = 0.55$ ,${T_2} = 1.05$ Figure 6. A plot of the result of the neural network training. The x-axis is the temperature, the State indicates the pro-bability that the sample at each temperature is recognized as a certain state, S indicates the state labeling method, T indicates the temperature labeling method, SS indicates the single-striped adsorption state, MS indicates the multi-striped adsorption state, and DE indicates desorbed state. The figure shows the learning results of two kinds of labeling methods. The recognition rate of convolutional network is 94.78%, where the AUC value is 0.9930. the fully connected network is 93.85%, where the AUC value is 0.9918, and the critical phase transition temperature of state labeling method is 0.55 and 1.1. The critical phase transition temperature of the temperature labeling method is 0.55 and 1.05.
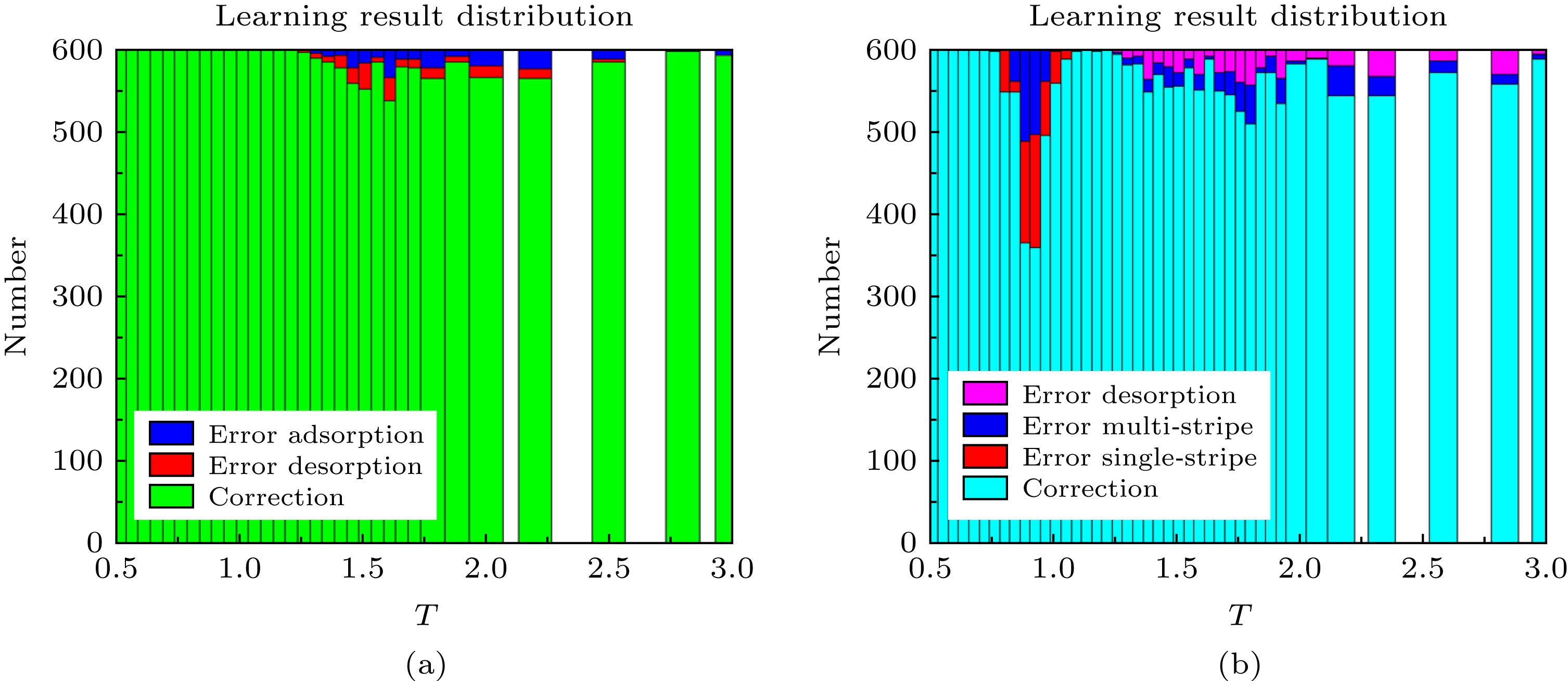
图 7 神经网络学习结果的分布图 (a) 均质表面下的学习结果分布, 绿色表示识别正确的样本, 其他的表示识别错误的样本; (b) 条纹表面下的学习结果分布, 蓝色表示识别正确的样本, 其他的表示识别错误的样本
Figure 7. The distribution of neural network learning results: (a) the distribution of learning outcomes on the homogeneous surface, green indicates that the correct sample, and other samples that identify the error; (b) the distribution of learning results on the pattern-stripe surface, blue indicates that the correct sample, and other samples that identify the error.
-
[1] Wei Q, Melko R G, Chen J Z Y 2017 Phys. Rev. E 95 032504
[2] Carrasquilla J, Melko R G 2017 Nat. Phys. 13 431
Google Scholar
[3] 邢雪, 于德新, 田秀娟 2017 物理学报 66 230501
Google Scholar
Xing X, Yu D X, Tian X J 2017 Acta Phys. Sin. 66 230501
Google Scholar
[4] Deo R C 2015 Circulation 132 1920
Google Scholar
[5] Lin W Y, Hu Y H, Tsai C F 2012 IEEE. Trans. 42 421
[6] Deng L, Dong Y 2011 Twelfth Annual Conference of the International Speech Communication Association Florence, Italy, August 27–31, 2011 p2285
[7] He K, Zhang X, Ren S 2016 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, USA, June26–July 1, 2016 p770
[8] Sun Q S, Zeng S G, Liu Y 2005 Pattern Recognit. 38 2437
Google Scholar
[9] Porter E W 1989 US Patent 4 829
[10] Jacobs P E, Chang C 1999 US Patent 5 956
[11] Berger A L, Pietra V J D, Pietra S A D 1996 Comput. Linguist. 22 39
[12] Brill E 1995 Comput. Linguist. 21 543
[13] McIlroy G T, Kees J E, Kalscheuer J A 1996 US Patent 5 583
[14] Anneroth G, Batsakis J, Luna M 1987 Eur. J. Oral Sci. 95 229
Google Scholar
[15] Carleo G, Troyer M 2017 Science 355 602
Google Scholar
[16] Ali J B, Fnaiech N, Saidi L 2015 Appl. Acoust. 89 16
Google Scholar
[17] Wang L, Zeng Y, Chen T 2015 Expert Syst. Appl. 42 855
Google Scholar
[18] Vogl T P, Mangis J K, Rigler A K 1988 Biol. Cybern. 59 257
Google Scholar
[19] Li H, Qian C J, Luo M B 2012 J. Appl. Polym. Sci. 124 282
Google Scholar
[20] Li H, Qian C J, Sun L Z 2010 Polym. J. 42 383
Google Scholar
[21] Li H, Qian C J, Wang C 2013 Phys. Rev. E 87 012602
Google Scholar
[22] Li H, Gong B, Qian C J 2013 Sens. Transducers J. 159 242
[23] Luo M B 2008 J. Chem. Phys. 128 044912
Google Scholar
[24] Luo M B, Huang J H 2003 J. Chem. Phys. 119 2439
Google Scholar
[25] Luo M, Huang J, Chen Y 2001 Eur. Polym. J. 37 1587
Google Scholar
[26] Chib S, Greenberg E 1995 Am. Stat. 49 327
[27] Haario H, Saksman E, Tamminen J 2001 Bernoulli 7 223
Google Scholar
[28] Hanley J A, McNeil B J 1982 Radiology 143 29
Google Scholar
[29] Bradley A P 1997 Pattern. Recognit. 30 1145
Google Scholar
[30] Li H, Gong B, Qian C J, Luo M B 2015 Soft Matter 11 3222
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7882
- PDF Downloads: 66
- Cited By: 0
