Identifying phase transition point of J1-J2 antiferromagnetic Heisenberg spin chain by machine learning

Wang Wei; Jie Quan-Lin

doi:10.7498/aps.70.20210711

Abstract

Studying quantum phase transitions through order parameters is a traditional method, but studying phase transitions by machine learning is a brand new field. The ability of machine learning to classify, identify, or interpret massive data sets may provide physicists with similar analyses of the exponentially large data sets embodied in the Hilbert space of quantum many-body system. In this work, we propose a method of using unsupervised learning algorithm of the Gaussian mixture model to classify the state vectors of the J₁-J₂ antiferromagnetic Heisenberg spin chain system, then the supervised learning algorithm of the convolutional neural network is used to identify the classification point given by the unsupervised learning algorithm, and the cross-validation method is adopted to verify the learning effect. Using this method, we study the J₁-J₂ Heisenberg spin chain system with chain length N = 8, 10, 12, 16 and obtain the same conclusion. The first order phase transition point of J₁-J₂ antiferromagnetic Heisenberg spin chain system can be accurately found from the ground state vector, but the infinite order phase transition point cannot be found from the ground state vector. The first order and the infinite order phase transition point can be found from the first excited state vector, which indirectly shows that the first excited state may contain more information than the ground state of J₁-J₂ antiferromagnetic Heisenberg spin chain system. The visualization of the state vector shows the reliability of the machine learning algorithm, which can extract the feature information from the state vector. The result reveals that the machine learning techniques can directly find some possible phase transition points from a large set of state vectorwithout prior knowledge of the energy or locality conditions of the Hamiltonian, which may assists us in studying unknown systems. Supervised learning can verify the phase transition points given by unsupervised learning, thereby indicating that we can discover some useful information about unknown systems only through machine learning techniques. Machine learning techniques can be a basic research tool in strong quantum-correlated systems, and it can be adapted to more complex systems, which can help us dig up hidden information.

Keywords:

Authors and contacts

School of Physics and Technology, Wuhan University, Wuhan 430000, China

Corresponding author: Jie Quan-Lin, qljie@whu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 1217050658)

FullText HTML : translate this paragraph

References

[1]	Lei W 2016 Phys. Rev. B. 94 195105 Google Scholar
[2]	Wetzel S J 2017 Phys. Rev. E 96 022140 Google Scholar
[3]	Huang L, Wang L 2017 Phys. Rev. B 95 035105 Google Scholar
[4]	Phiala E S, Daniel T, William D 2018 Phys. Rev. D 97 094506 Google Scholar
[5]	LakovlevI A, SotnikovO M, MazurenkoV V 2018 Phys. Rev. B 98 174411 Google Scholar
[6]	Dong X Y, Pollmann F, Zhang X F 2019 Phys. Rev. B 99 121104 Google Scholar
[7]	Tan D R, Jiang F J 2020 Phys. Rev. B 102 224434 Google Scholar
[8]	Tan D R, Li C D, Zhu W P, Jiang F J 2020 New J. Phys. 22 063016 Google Scholar
[9]	Maskara N, Buchhold M, Endres M 2021 arXiv: 2103.15855 [quant-ph]
[10]	Tanja D 2021 arXiv: 2103.07236[quant-ph]
[11]	Sondhi S L, Girvin S M, Carini J P, Shahar D 1997 Rev. Mod. Phys 69 315 Google Scholar
[12]	Bulla R, Vojta M 2003 Rep. Prog. Phys. 66 2069 Google Scholar
[13]	Walker N, Tam K M, Novak B, Jarrell M 2018 Phys. Rev. E. 98 053305 Google Scholar
[14]	Jadrich R B, Lindquist B A, Pineros W D, Truskeet T M 2018 J. Chem. Phys. 149 194109 Google Scholar
[15]	Canabarro A, Fanchini F F, Malvezzi A L, Pereira R, Chaves R 2019 Phys. Rev. B 100 045129 Google Scholar
[16]	Carrasquilla J, Melko R G 2017 Nat. Phys. 13 431 Google Scholar
[17]	Ahmadreza A, Michel P 2020 arXiv: 2007.09764 [cond-mat. stat-mech]
[18]	Chitra R, Pati S, Krishnamurthy H R, Sen D, Ramasesha S 1995 Phys. Rev. B 52 6581 Google Scholar
[19]	Castilla G, Chakravarty S, Emery V J 1995 Phys. Rev. L 75 1823 Google Scholar
[20]	Shu C, Li W, Shi J G, Wang Y P 2007 Phys. Rev. E 76 061108 Google Scholar
[21]	Qian X F, Shi T, Li Y, Song Z, Sun C P 2005 Phys. Rev. A 72 012333 Google Scholar
[22]	周志华 2016 机器学习 (北京: 清华大学出版社) 第206页 Zhou Z H 2016 Machine Learning (Beijing: Tsinghua University Press) p206 (in Chinese)
[23]	李航 2012 统计机器学习 (北京: 清华大学出版社) 第162页 Li H 2012The Elements of Statistical Learning (Beijing: Tsinghua University Press) p162 (in Chinese)
[24]	徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 物理学报 69 014209 Google Scholar Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209 Google Scholar
[25]	伊恩·古德费洛, 约书亚·本吉奥, 亚伦·库维尔著 (赵申剑, 黎彧君, 符天凡, 李凯译) 2017 深度学习 (北京:人民邮电出版社) 第143—317页 Goodfellow L, Bengio Y, Courville A（translated by Zhang SJ, Li Y J, Fu T F, Li K）2017 Deep Learning (Beijing: The People's Posts and Telecommunications Press) pp143–317 (in Chinese)

Cited By

图 1 不同链长的 J₁-J₂海森伯自旋链系统基态与第一激发态能量随J₂/J₁的变化　(a) N = 8; (b) N = 10; (c) N = 12; (d) N = 16

Figure 1. Ground and first excited energy level diagram in J₁-J₂ Heisenberg spin chain system with chain length: (a) N = 8; (b) N = 10; (c) N = 12; (d) N = 16.

DownLoad: Full-Size Img PowerPoint

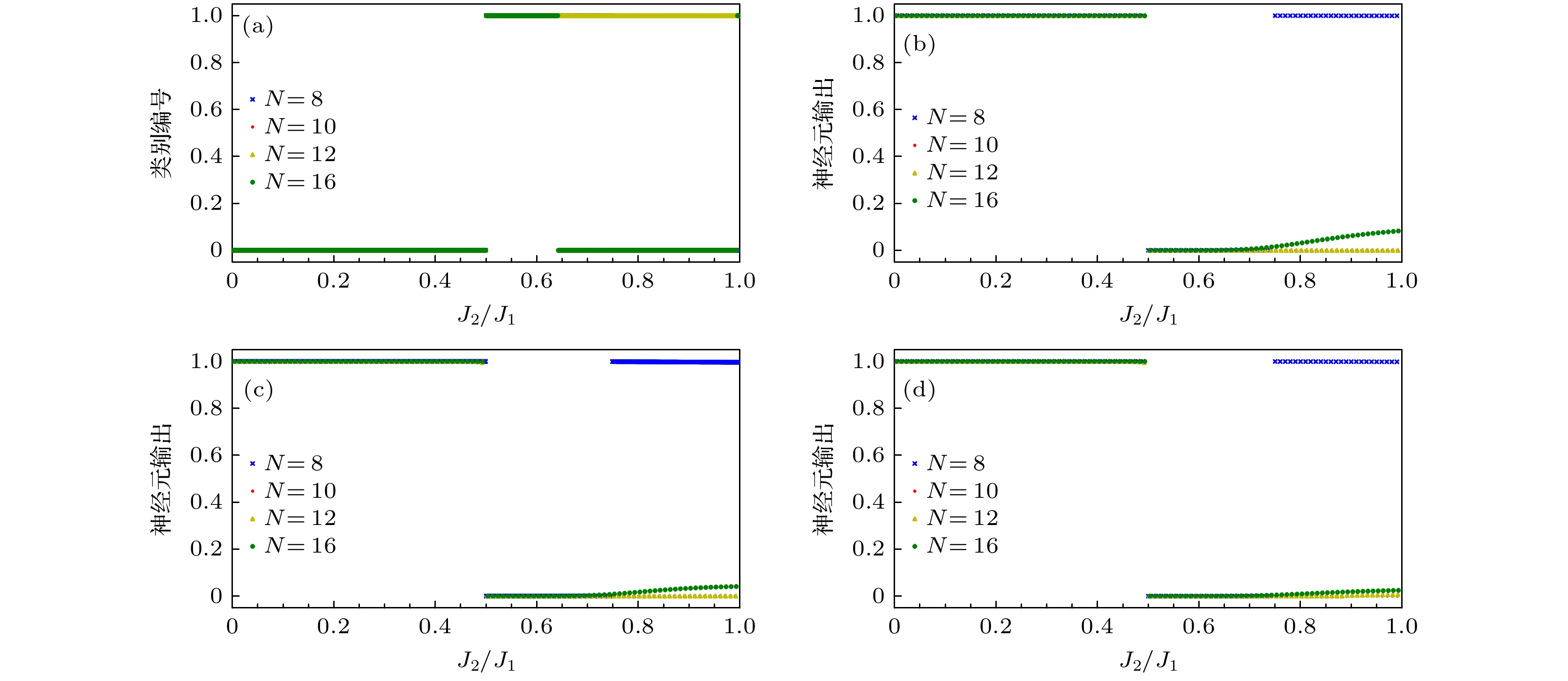
图 2 (a) 训练数据为J₂/J₁$\in $[0, 1)的海森伯J₁-J₂模型基态矢量生成的GMM对基态矢量的分类结果; (b)采用标记为0的J₂/J₁$\in $[0.35, 0.45)和为1的J₂/J₁$\in $[0.55, 0.65); (c)标记为0的J₂/J₁$\in $[0.3, 0.4)和为1的J₂/J₁$\in $[0.55, 0.65); (d)标记为0的J₂/J₁$\in $[0.2, 0.3)和为1的J₂/J₁$\in $[0.55, 0.65)的基态态矢量作为训练数据, 训练所得的CNN模型对基态态矢量的预测结果

Figure 2. (a) Ground state vector classification results of the GMM generated by the Heisenberg J₁-J₂ model ground state vector with the training data of J₂/J₁$\in $ [0, 1); (b) using the ground state vector of J₂/J₁$\in $[0.35, 0.45) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1; (c) J₂/J₁$\in $[0.3, 0.4) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1; (d) J₂/J₁$\in $[0.2, 0.3) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1 as training data, the prediction results of the ground state vector by the trained convolutional neural network model.

DownLoad: Full-Size Img PowerPoint

图 3 (a) 训练数据为J₂/J₁$\in $[0, 0.5)的海森伯J₁-J₂模型基态态矢量生成的GMM对基态态矢量的分类结果; (b) 分别为采用标记为0的J₂/J₁$\in $[0.25, 0.3)和为1的J₂/J₁$\in $[0.35, 0.4); (c)标记为0的J₂/J₁$\in $[0.2, 0.25)和为1的J₂/J₁$\in $[0.35, 0.4); (d)标记为0的J₂/J₁$\in $[0.2, 0.25)和为1的J₂/J₁$\in $[0.35, 0.4)(标记为1的数据是标记为0的5倍)的基态态矢量作为训练数据, 训练所得的CNN模型对基态态矢量的预测结果

Figure 3. (a) Ground state vector classification results of the GMM generated by the Heisenberg J₁-J₂ model ground state vector with the training data of J₂/J₁$\in $ [0, 0.5); (b) respectively usingthe ground state vector of J₂/J₁$\in $[0.25, 0.3) marked as 0 and J₂/J₁$\in $[0.35, 0.4) marked as 1; (c) J₂/J₁$\in $[0.2, 0.25) marked as 0 and J₂/J₁$\in $[0.35, 0.4) marked as 1; (d) J₂/J₁$\in $[0.2, 0.25) marked as 0 and J₂/J₁$\in $[0.35, 0.4) marked as 1 (the data marked as 1 is 5 times as much as the data marked as 0)as training data, the prediction results of the ground state vector by the trained convolutional neural network model.

DownLoad: Full-Size Img PowerPoint

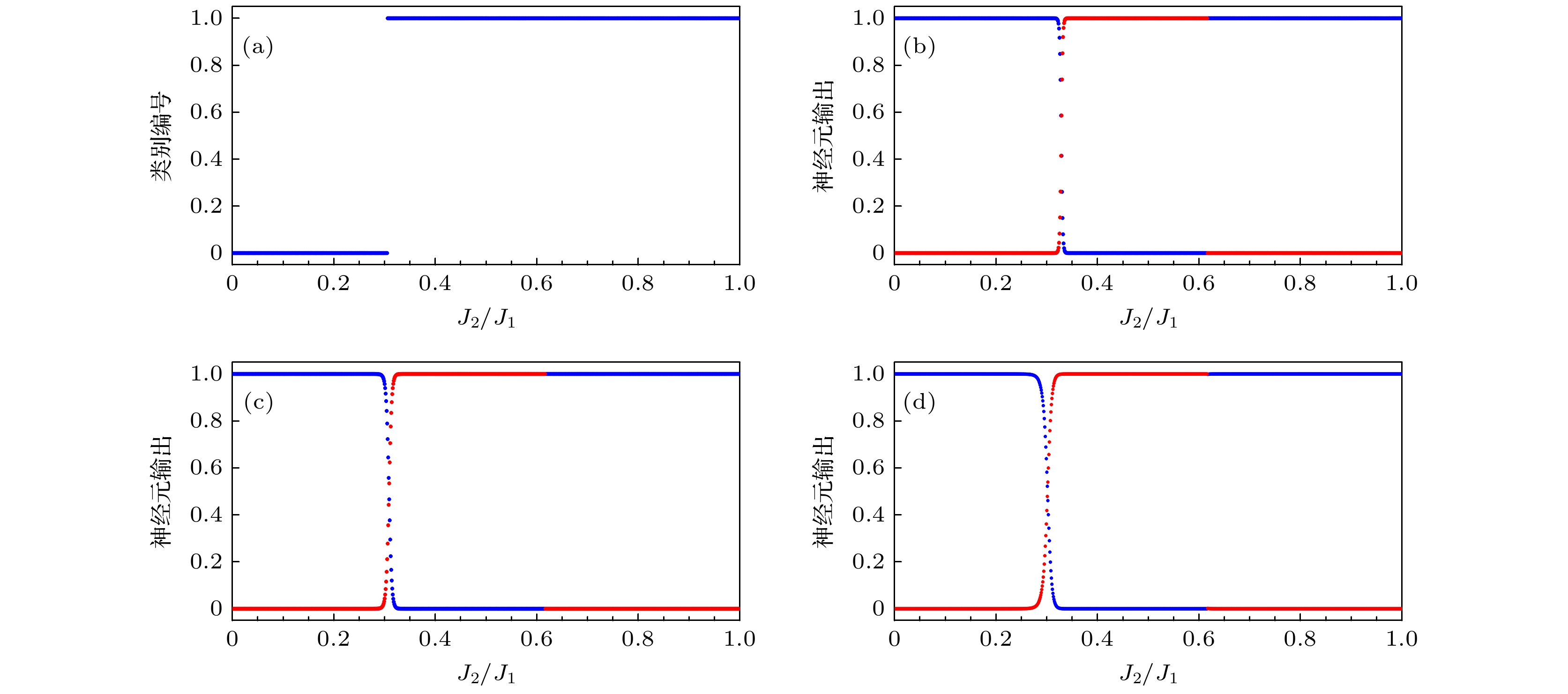
图 4 (a) 训练数据为J₂/J₁$\in $[0, 1)的海森伯J₁-J₂模型第一激发态态矢量生成的GMM对第一激发态态矢量的分类结果; (b)分别为采用标记为0的J₂/J₁$\in $[0.35, 0.45)和为1的J₂/J₁$\in $[0.55, 0.65); (c)标记为0的J₂/J₁$\in $[0.3, 0.4)和为1的J₂/J₁$\in $[0.55, 0.65); (d)标记为0的J₂/J₁$\in $[0.35, 0.45)和为1的J₂/J₁$\in $[0.55, 0.65) (标记为1的数据是标记为0的5倍)的第一激发态态矢量作为训练数据, 训练所得的CNN模型对第一激发态态矢量的预测结果

Figure 4. (a) The first excited state vector classification results of the GMM generated by the Heisenberg J₁-J₂ model first excited state vector with the training data of J₂/J₁ $\in $ [0, 1); (b) using the first excited state vector of J₂/J₁$\in $[0.35, 0.45) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1; (c) J₂/J₁$\in $[0.3, 0.4) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1; (d) J₂/J₁$\in $[0.35, 0.45) marked as 0 and J₂/J₁$\in $[0.55, 0.65) marked as 1 (the data marked as 1 is 5 times as much as the data marked as 0)as training data, the prediction results of the first excited state vector by the trained convolutional neural network model.

DownLoad: Full-Size Img PowerPoint

图 5 (a)采用标记为0的J₂/J₁$\in $[0.1, 0.2), 标记为1的J₂/J₁$\in $[0.3, 0.4); (b)标记为0的J₂/J₁$\in $[0, 0.1), 标记为1的J₂/J₁$\in $[0.3, 0.4)的第一激发态态矢量作为训练数据, 训练所得的CNN模型对第一激发态态矢量的预测结果

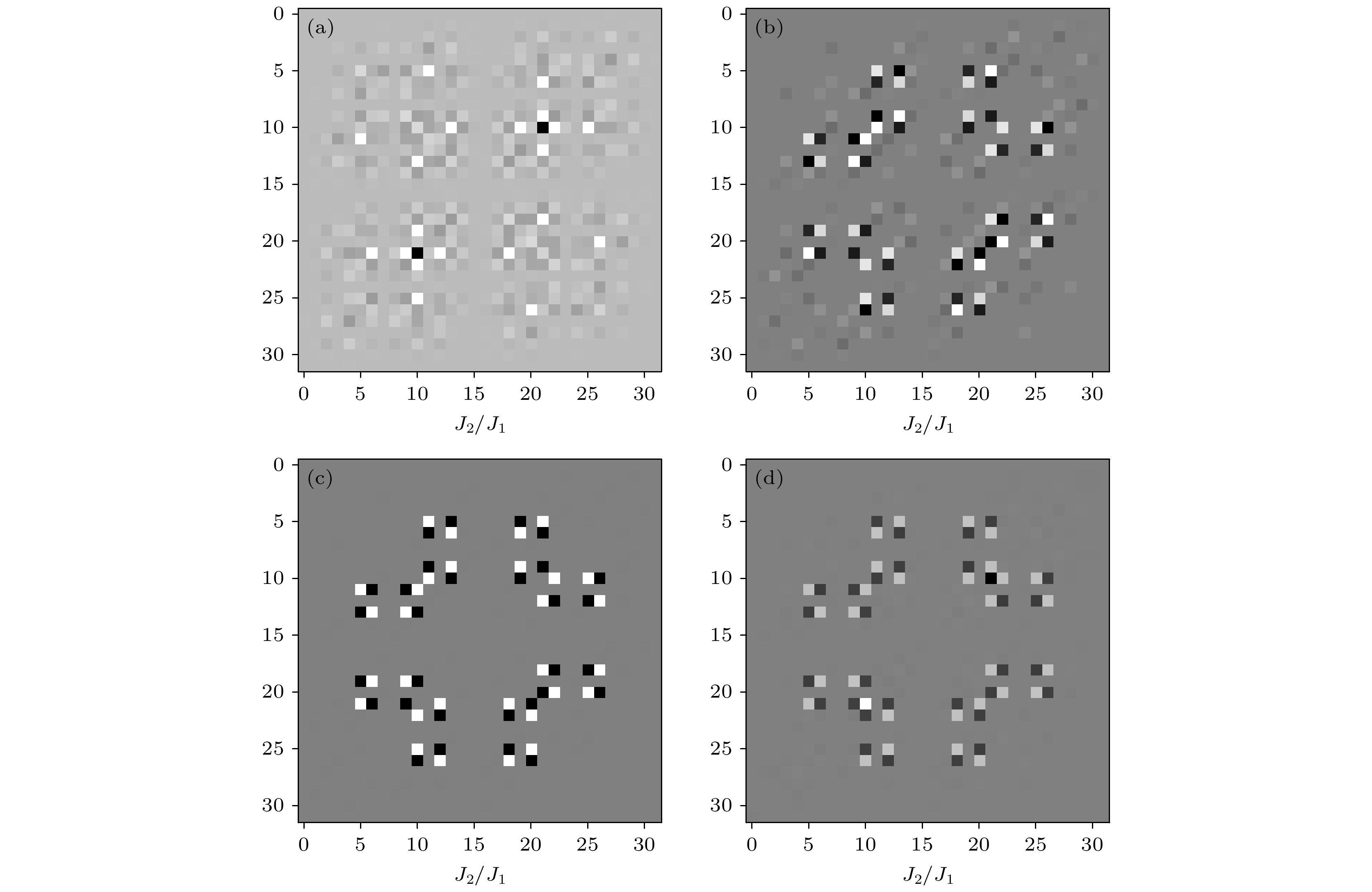
Figure 5. (a) Using the first excited state vector of J₂/J₁$\in $[0.1, 0.2) marked as 0 and J₂/J₁$\in $[0.3, 0.4) marked as 1; (b)J₂/J₁$\in $[0, 0.1) marked as 0 and J₂/J₁$\in $[0.3, 0.4) marked as 1 as training data, the prediction results of the first excited state vector by the trained convolutional neural network model.

DownLoad: Full-Size Img PowerPoint

图 6 (a) 训练数据为J₂/J₁$\in $[0, 0.24)的海森伯J₁-J₂模型第一激发态态矢量生成的GMM对第一激发态态矢量的分类结果; (b), (c)分别为采用标记为0的J₂/J₁$\in $[0.05, 0.1)和为1的J₂/J₁$\in $[0.15, 0.2); 标记为0的J₂/J₁$\in $[0, 0.05)和为1的J₂/J₁$\in $[0.15, 0.2)的第一激发态态矢量作为训练数据, 训练所得的CNN模型对第一激发态态矢量的预测结果; (d) 训练数据为J₂/J₁$\in $[0.25, 0.5)的海森伯J₁-J₂模型第一激发态态矢量生成的GMM对第一激发态态矢量的分类结果

Figure 6. (a) The first excited state vector classification results of the GMM generated by the Heisenberg J₁-J₂ model first excited state vector with the training data of J₂/J₁ $\in $ [0, 0.24); (b) (c) respectively using the first excited state vector of J₂/J₁$\in $[0.05, 0.1) marked as 0 and J₂/J₁$\in $[0.15, 0.2) marked as 1; J₂/J₁$\in $[0, 0.05) marked as 0 and J₂/J₁$\in $[0.15, 0.2) marked as 1 as training data, the prediction results of the first excited state vector by the trained convolutional neural network model; (d) he first excited state vector classification results of the GMM generated by the Heisenberg J₁-J₂ model first excited state vector with the training data of J₂/J₁$\in $[0.25, 0.5).

DownLoad: Full-Size Img PowerPoint

图 7 海森伯 J₁-J₂模型基态态矢量变换而来的灰度图　(a) J₂/J₁ = 0.44; (b) J₂/J₁ = 0.49; (c) J₂/J₁ = 0.51; (d) J₂/J₁ = 0.58

Figure 7. Gray scale images transformed from the ground state vector of the Heisenberg J₁-J₂ model: (a) J₂/J₁ = 0.44; (b) J₂/J₁ = 0.49; (c) J₂/J₁ = 0.51; (d) J₂/J₁ = 0.58.

DownLoad: Full-Size Img PowerPoint

图 8 海森伯J₁-J₂模型第一激发态态矢量变换而来的灰度图　(a) J₂/J₁ = 0.24; (b) J₂/J₁ = 0.25; (c) J₂/J₁ = 0.49; (d) J₂/J₁ = 0.51

Figure 8. Gray scale images transformed from the first excited state vector of the Heisenberg J₁-J₂ model: (a) J₂/J₁ = 0.24; (b) J₂/J₁ = 0.25; (c) J₂/J₁ = 0.49; (d) J₂/J₁ = 0.51.

DownLoad: Full-Size Img PowerPoint

[1]	Lei W 2016 Phys. Rev. B. 94 195105 Google Scholar
[2]	Wetzel S J 2017 Phys. Rev. E 96 022140 Google Scholar
[3]	Huang L, Wang L 2017 Phys. Rev. B 95 035105 Google Scholar
[4]	Phiala E S, Daniel T, William D 2018 Phys. Rev. D 97 094506 Google Scholar
[5]	LakovlevI A, SotnikovO M, MazurenkoV V 2018 Phys. Rev. B 98 174411 Google Scholar
[6]	Dong X Y, Pollmann F, Zhang X F 2019 Phys. Rev. B 99 121104 Google Scholar
[7]	Tan D R, Jiang F J 2020 Phys. Rev. B 102 224434 Google Scholar
[8]	Tan D R, Li C D, Zhu W P, Jiang F J 2020 New J. Phys. 22 063016 Google Scholar
[9]	Maskara N, Buchhold M, Endres M 2021 arXiv: 2103.15855 [quant-ph]
[10]	Tanja D 2021 arXiv: 2103.07236[quant-ph]
[11]	Sondhi S L, Girvin S M, Carini J P, Shahar D 1997 Rev. Mod. Phys 69 315 Google Scholar
[12]	Bulla R, Vojta M 2003 Rep. Prog. Phys. 66 2069 Google Scholar
[13]	Walker N, Tam K M, Novak B, Jarrell M 2018 Phys. Rev. E. 98 053305 Google Scholar
[14]	Jadrich R B, Lindquist B A, Pineros W D, Truskeet T M 2018 J. Chem. Phys. 149 194109 Google Scholar
[15]	Canabarro A, Fanchini F F, Malvezzi A L, Pereira R, Chaves R 2019 Phys. Rev. B 100 045129 Google Scholar
[16]	Carrasquilla J, Melko R G 2017 Nat. Phys. 13 431 Google Scholar
[17]	Ahmadreza A, Michel P 2020 arXiv: 2007.09764 [cond-mat. stat-mech]
[18]	Chitra R, Pati S, Krishnamurthy H R, Sen D, Ramasesha S 1995 Phys. Rev. B 52 6581 Google Scholar
[19]	Castilla G, Chakravarty S, Emery V J 1995 Phys. Rev. L 75 1823 Google Scholar
[20]	Shu C, Li W, Shi J G, Wang Y P 2007 Phys. Rev. E 76 061108 Google Scholar
[21]	Qian X F, Shi T, Li Y, Song Z, Sun C P 2005 Phys. Rev. A 72 012333 Google Scholar
[22]	周志华 2016 机器学习 (北京: 清华大学出版社) 第206页 Zhou Z H 2016 Machine Learning (Beijing: Tsinghua University Press) p206 (in Chinese)
[23]	李航 2012 统计机器学习 (北京: 清华大学出版社) 第162页 Li H 2012The Elements of Statistical Learning (Beijing: Tsinghua University Press) p162 (in Chinese)
[24]	徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 物理学报 69 014209 Google Scholar Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209 Google Scholar
[25]	伊恩·古德费洛, 约书亚·本吉奥, 亚伦·库维尔著 (赵申剑, 黎彧君, 符天凡, 李凯译) 2017 深度学习 (北京:人民邮电出版社) 第143—317页 Goodfellow L, Bengio Y, Courville A（translated by Zhang SJ, Li Y J, Fu T F, Li K）2017 Deep Learning (Beijing: The People's Posts and Telecommunications Press) pp143–317 (in Chinese)

[1]	Zhang Jia-Hui. Machine learning for in silico protein research. Acta Physica Sinica, 2024, 73(6): 069301. doi: 10.7498/aps.73.20231618
[2]	Ouyang Xin-Jian, Zhang Yan-Xing, Wang Zhi-Long, Zhang Feng, Chen Wei-Jia, Zhuang Yuan, Jie Xiao, Liu Lai-Jun, Wang Da-Wei. Modeling ferroelectric phase transitions with graph convolutional neural networks. Acta Physica Sinica, 2024, 73(8): 086301. doi: 10.7498/aps.73.20240156
[3]	Luo Qi-Rui, Shen Yi-Fan, Luo Meng-Bo. Computer simulation and machine learning of polymer collapse and critical adsorption phase transitions. Acta Physica Sinica, 2023, 72(24): 240502. doi: 10.7498/aps.72.20231058
[4]	Zhang Yi-Fan, Ren Wei, Wang Wei-Li, Ding Shu-Jian, Li Nan, Chang Liang, Zhou Qian. Machine learning combined with solid solution strengthening model for predicting hardness of high entropy alloys. Acta Physica Sinica, 2023, 72(18): 180701. doi: 10.7498/aps.72.20230646
[5]	Guo Wei-Chen, Ai Bao-Quan, He Liang. Reveal flocking phase transition of self-propelled active particles by machine learning regression uncertainty. Acta Physica Sinica, 2023, 72(20): 200701. doi: 10.7498/aps.72.20230896
[6]	Tian Cheng, Lan Jian-Xiong, Wang Cang-Long, Zhai Peng-Fei, Liu Jie. First-principles study of phase transition of BaF ₂ under high pressue. Acta Physica Sinica, 2022, 71(1): 017102. doi: 10.7498/aps.71.20211163
[7]	Zhao Zhong-Hua, Qu Guang-Hao, Yao Jia-Chi, Min Dao-Min, Zhai Peng-Fei, Liu Jie, Li Sheng-Tao. Molecular dynamics simulation of phase transition by thermal spikes in monoclinic ZrO₂. Acta Physica Sinica, 2021, 70(13): 136101. doi: 10.7498/aps.70.20201861
[8]	. Phase transition of BaF2 under high pressue studied by a first-principles study. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211163
[9]	Liu Wu, Zhu Cheng-Wan, Li Hao-Tian, Zhao Su-Ling, Qiao Bo, Xu Zheng, Song Dan-Dan. Optimization of Ga content gradient in Cu(In,Ga)Se₂ solar cells through machine learning and device simulation. Acta Physica Sinica, 2021, 70(23): 238802. doi: 10.7498/aps.70.20211234
[10]	Zhang Yao, Zhang Yun-Bo, Chen Li. Deep-learning-assisted micro impurity detection on an optical surface. Acta Physica Sinica, 2021, 70(16): 168702. doi: 10.7498/aps.70.20210403
[11]	Sun Li-Wang, Li Hong, Wang Peng-Jun, Gao He-Bei, Luo Meng-Bo. Recognition of adsorption phase transition of polymer on surface by neural network. Acta Physica Sinica, 2019, 68(20): 200701. doi: 10.7498/aps.68.20190643
[12]	Xu Ting-Ting, Li Yi, Chen Pei-Zu, Jiang Wei, Wu Zheng-Yi, Liu Zhi-Min, Zhang Jiao, Fang Bao-Ying, Wang Xiao-Hua, Xiao Han. Infrared modulator based on AZO/VO2/AZO sandwiched structure due to electric field induced phase transition. Acta Physica Sinica, 2016, 65(24): 248102. doi: 10.7498/aps.65.248102
[13]	Qu Yan-Dong, Kong Xiang-Qing, Li Xiao-Jie, Yan Hong-Hao. Effect of thermal treatment on the structural phase transformation of the detonation-prepared TiO2 mixed crystal nanoparticles. Acta Physica Sinica, 2014, 63(3): 037301. doi: 10.7498/aps.63.037301
[14]	Liu Zhi-Qiang, Chang Sheng-Jiang, Wang Xiao-Lei, Fan Fei, Li Wei. Thermally controlled terahertz metamaterial modulator based on phase transition of VO2 thin film. Acta Physica Sinica, 2013, 62(13): 130702. doi: 10.7498/aps.62.130702
[15]	Li Yan, Tang Gang, Song Li-Jiang, Xun Zhi-Peng, Xia Hui, Hao Da-Peng. Numerical simulations of the phase transition property of the explosive percolation model on Erds Rnyi random network. Acta Physica Sinica, 2013, 62(4): 046401. doi: 10.7498/aps.62.046401
[16]	Han Xiu-Qin, Jiang Hong, Shi Yu-Ren, Liu Yan-Xiu, Sun Jian-Hua, Chen Jian-Min, Duan Wen. Phase transition of atomic chain in the one-dimensional Frenkel-Kontorova model. Acta Physica Sinica, 2011, 60(11): 116801. doi: 10.7498/aps.60.116801
[17]	Fan Hua, Li Li, Yuan Jian, Shan Xiu-Ming. Langevin model of the flow control in the internet and its phase transition analysis. Acta Physica Sinica, 2009, 58(11): 7507-7513. doi: 10.7498/aps.58.7507
[18]	Shi Zhu-Yi, Ji Shi-Yin. Specific heat capacity and phase transition on 148—158Sm nucleiin microscopic core plus two-quasiparticle model. Acta Physica Sinica, 2003, 52(1): 42-47. doi: 10.7498/aps.52.42
[19]	YUAN JIAN, REN YONG, LIU FENG, SHAN XIU-MING. PHASE TRANSITION AND COLLECTIVE CORRELATION BEHAVIOR IN THE COMPLEX COMPUTER NETWORK. Acta Physica Sinica, 2001, 50(7): 1221-1225. doi: 10.7498/aps.50.1221
[20]	CHEN SHU, CHANG SHENG-JIANG, YUAN JING-HE, ZHANG YAN-XIN, K.W.WONG. ADAPTIVE TRAINING AND PRUNING FOR NEURAL NETWORKS:ALGORITHMS AND APPLICATION. Acta Physica Sinica, 2001, 50(4): 674-681. doi: 10.7498/aps.50.674

Catalog

Vol. 70, Issue 23 - 2021-12-05

Metrics

Abstract views: 4623
PDF Downloads: 112
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板

Identifying phase transition point of J₁-J₂ antiferromagnetic Heisenberg spin chain by machine learning