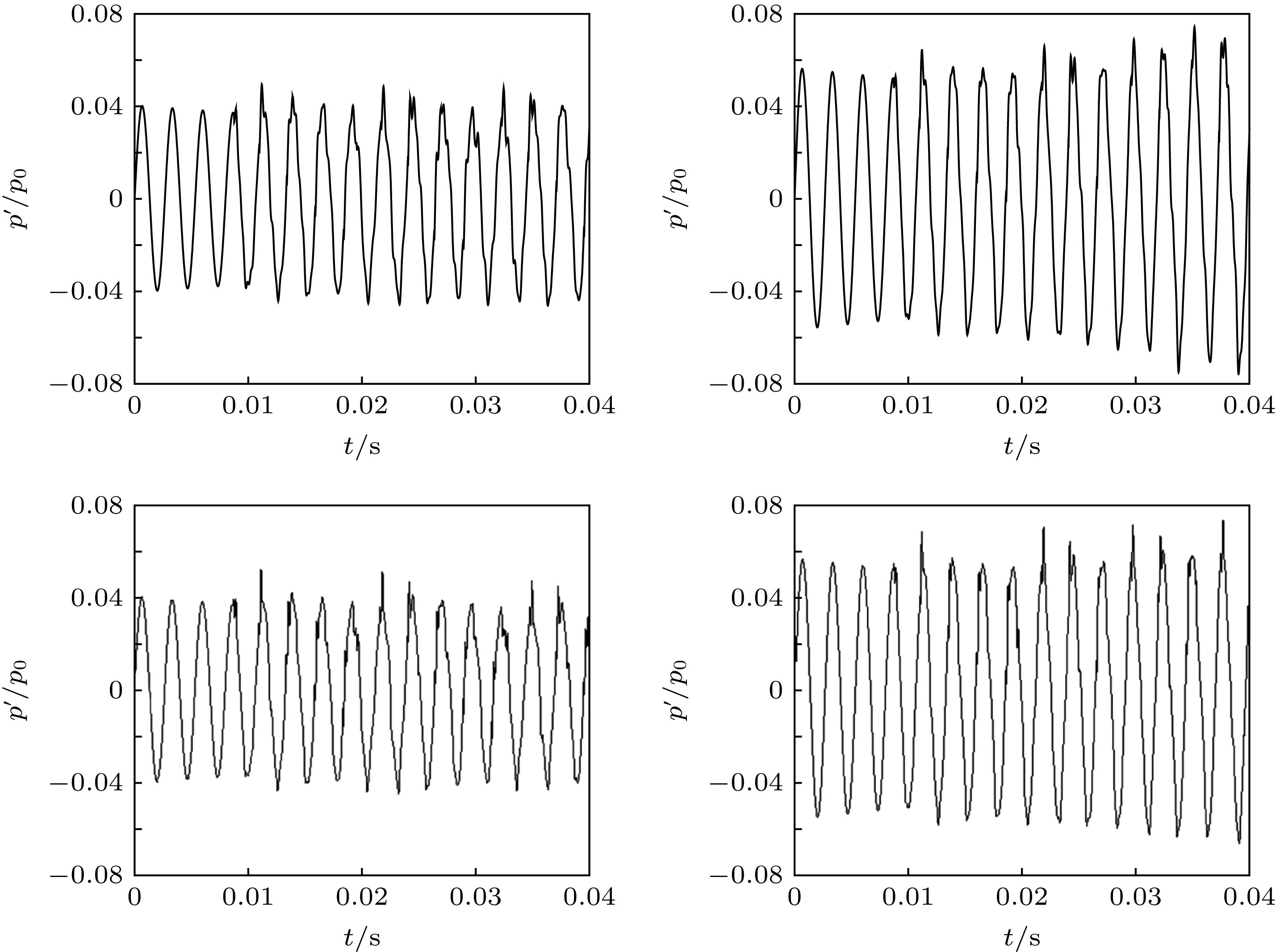
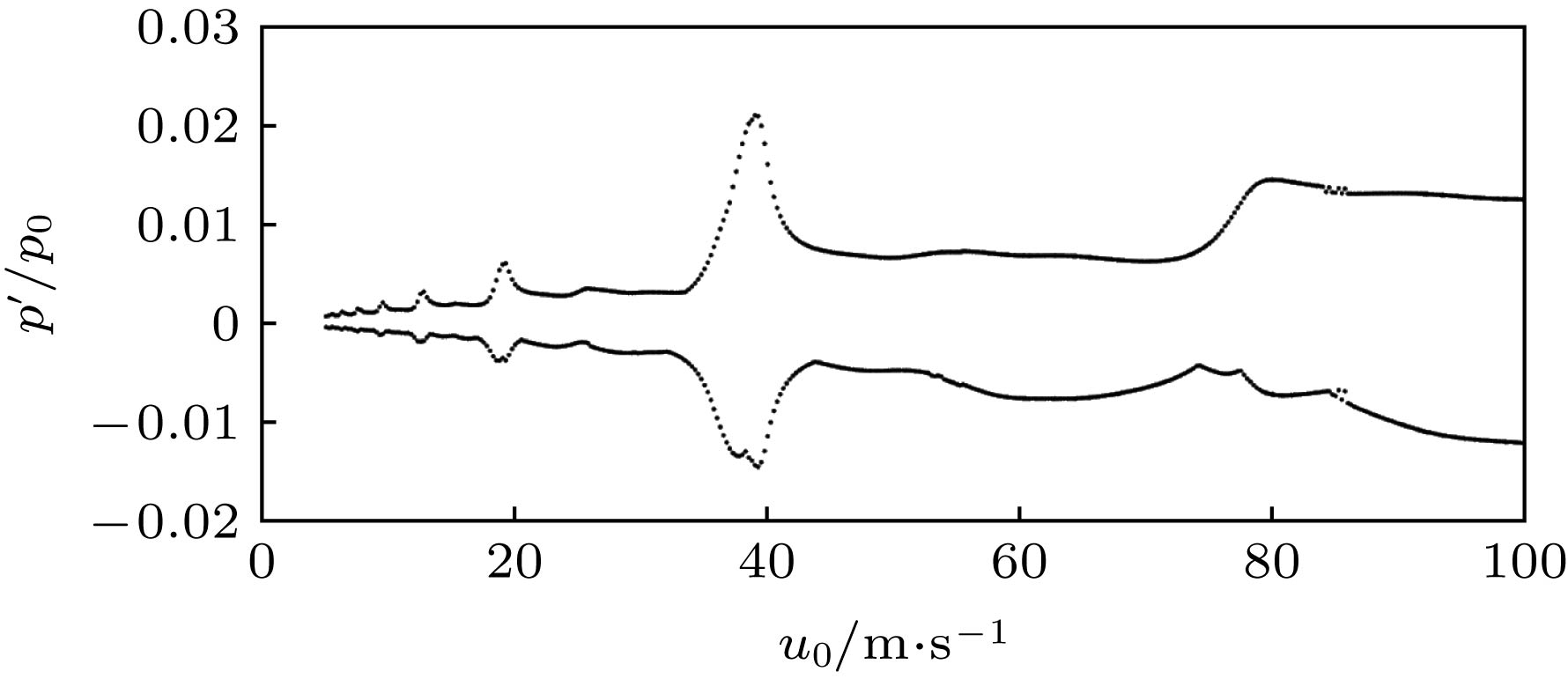
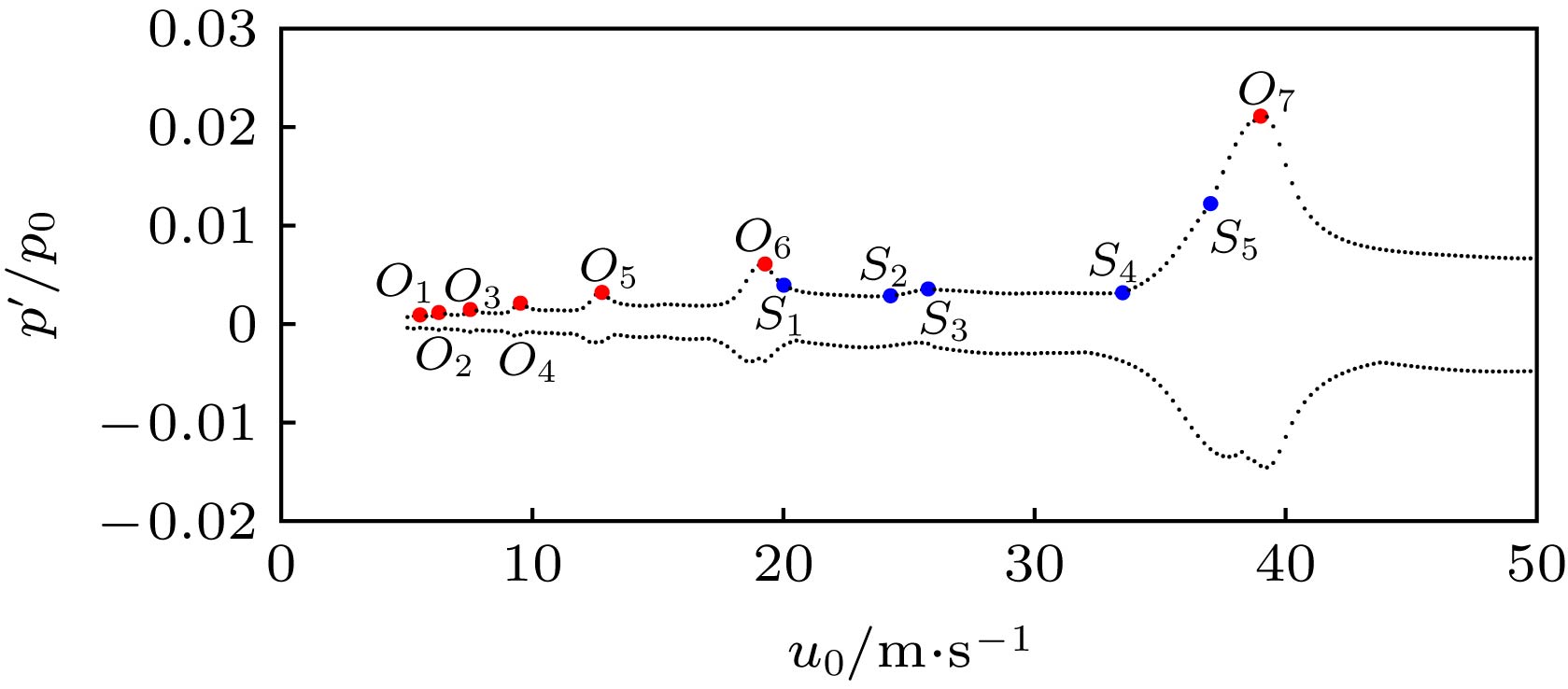
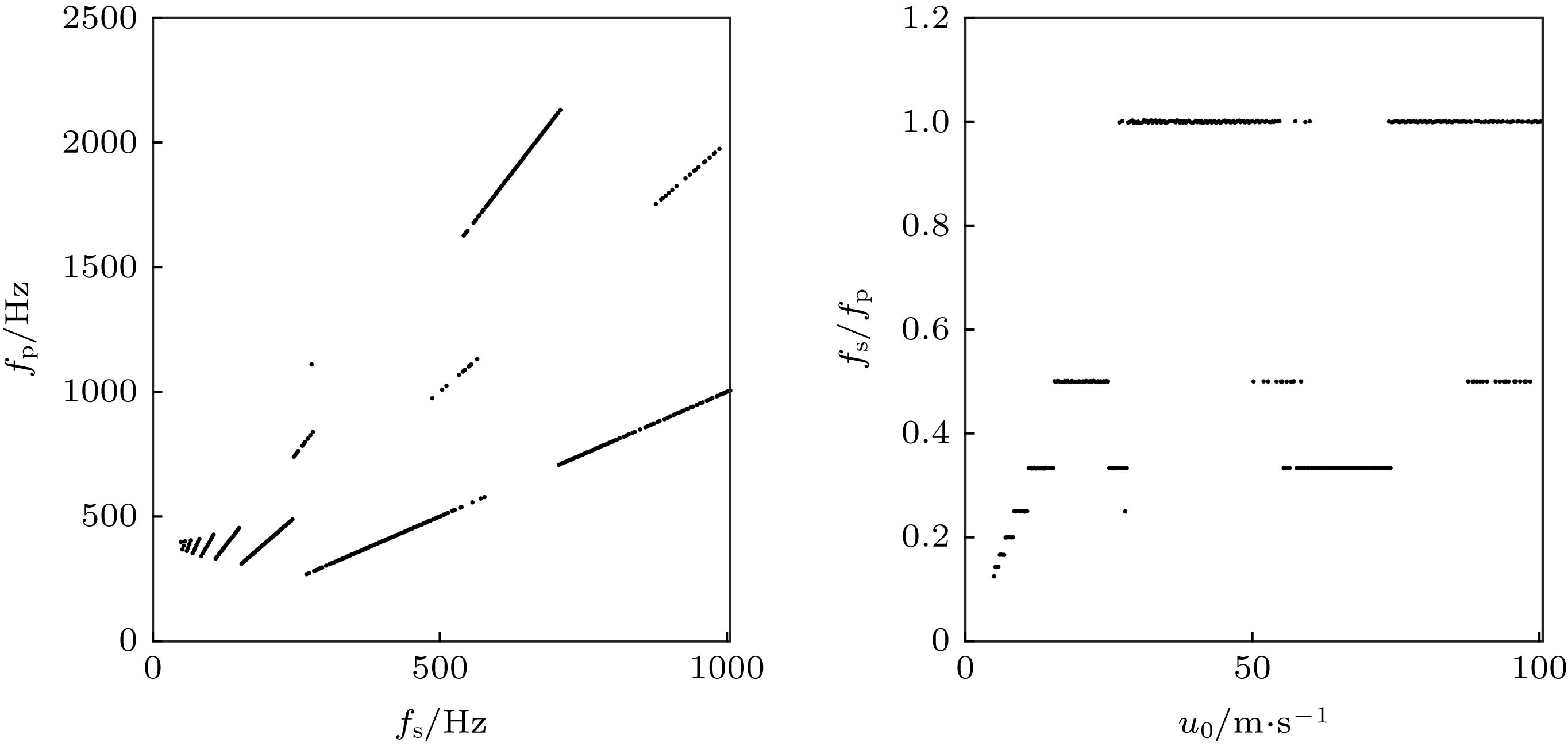
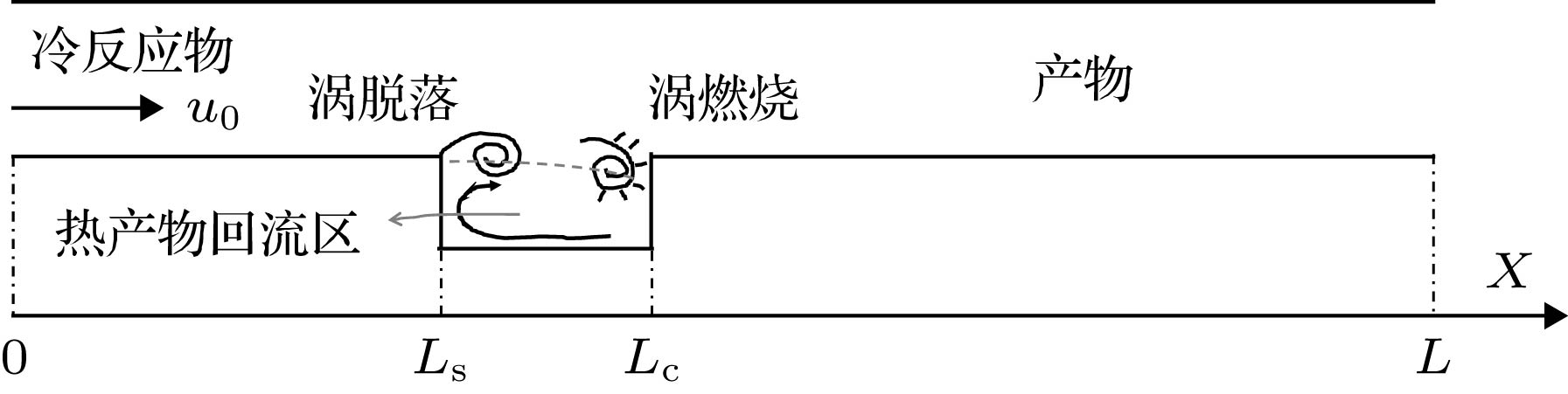
-
In engineering, the combustion chamber with a backward step is very popular, and it is a kind of flame stabilizer. In this type of combustion chamber, there will be shedding vortices at the step due to the instability of the flow field. The shedding vortices will carry reactants to move downstream and burn, resulting in unstable heat release and then pressure and velocity fluctuations of the sound field, thereby, finally, forming a combustion-vortex-acoustic interaction process. If a positive feedback loop is formed between the unstable heat release and the pressure fluctuation of sound field, combustion instability will occur, and it is also referred to as thermoacoustic oscillation due to vortex shedding. Combustion instability frequently occurs in many practical systems or equipment, and its induced significant pressure oscillations have a serious influence on the normal operation of the equipment. Recently, the combustion instability has been extensively studied experimentally, but the theoretical investigation on its nature is still rare. Since combustion instability is a complicated nonlinear phenomenon, it is necessary to study its nature from the viewpoint of nonlinear dynamics. Based on the one-dimensional simplified model of thermoacoustic instability involving vortex shedding proposed by Matveev and Culick, the typical nonlinear phenomenon in thermoacoustic oscillation induced by vortex shedding is studied. The study focuses on the initial value sensitivity of the system, the influence of key parameters on thermoacoustic oscillation, and the phenomenon of vortex-acoustic lock-on. Firstly, the Galerkin method is used to approximate the governing equation, and the partial differential equations are reduced to a set of ordinary differential equations. Then, the first ten modes are selected, and the pressure and velocity fluctuations of sound field under different system parameters are obtained by MATLAB program. Finally, the thermoacoustic instability of the system under different initial disturbances, the influences of different steady flow velocity on the thermoacoustic oscillation of the system, and the phenomenon of vortex-acoustic lock-on in thermoacoustic oscillation are studied in detail. The results show that the system of thermoacoustic oscillation involving vortex shedding is extremely sensitive to initial values, and there are a rich variety of nonlinear phenomena. With steady flow velocity increasing, the amplitude of pressure fluctuation augments generally. However, the similar structures are found in several intervals of steady flow velocity, and the amplitude first decreases and then increases. In particular, it is verified that the system oscillates periodically by integer (fp/fs) multiple of the vortex impinging frequency (fs), that is, the vortex-acoustic frequency locking with the number of revolutions fp/fs, which is found in experiment and can be regarded as an important characteristic of periodic thermoacoustic oscillation.
-
Keywords:
- thermoacoustic instability /
- vortex shedding /
- vortex-acoustic lock-on /
- similarity
[1] Zinn B T, Lieuwen T C 2005 Combustion IInstabilities: Basic Concepts 210 3
[2] Annaswamy A M, Ghoniem A F 2002 IEEE Control Syst. Mag. 22 37
Google Scholar
[3] Balasubramanian K, Sujith R I 2008 Phys. Fluids 20 44
[4] Subramanian P, Mariappan S, Sujith R I, Wahi P 2010 Int. J. Spray Combust. 2 325
Google Scholar
[5] 党南南, 张正元, 张家忠 2018 物理学报 67 134301
Google Scholar
Dang N N, Zhang Z Y, Zhang J Z 2018 Acta Phys. Sin. 67 134301
Google Scholar
[6] Rogers D E 1956 Jet Propul. 26 456
Google Scholar
[7] Hegde U G, Reuter D, Daniel B R, Zinn B T 1987 Combust. Sci. Technol. 55 125
Google Scholar
[8] Poinsot T J, Trouve A C, Veynante D P, Candel S M, Esposito E J 1987 J. Fluid Mech. 177 265
Google Scholar
[9] Sterling J D, Zukoski E E 1991 Combust. Sci. Technol. 77 225
Google Scholar
[10] Cohen J, Anderson T 1996 34th Aerospace Sciences Meeting and Exhibit Reno, January 15−18, 1996 p819
[11] Speth R, Altay H, Hudgins D, Annaswamy A, Ghoniem A 2008 46th AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 7–10, 2008 p1053
[12] Bauwens L, Daily J W 1992 J. Propul. Power 8 264
Google Scholar
[13] Najm H N, Ghoniem 1993 Combust. Sci. Technol. 94 259
Google Scholar
[14] Menon S, Jou W H 1991 Combust. Sci. Technol. 75 53
Google Scholar
[15] Angelberger C, Veynante D, Egolfopoulos F 2000 Flow Turbul. Combust. 65 205
Google Scholar
[16] Qin F, He G Q, Li J, Liu P J 2007 43rd AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit Cincinnati, OH, July 8–11, 2007 p5748
[17] 万少文, 何国强, 石磊 2011 固体火箭技术 34 32
Google Scholar
Wan S W, He G Q, Shi L 2011 Journal of Solid Rocket Technology 34 32
Google Scholar
[18] Matveev K I, Culick F E C 2003 Combust. Sci. Technol. 175 1059
Google Scholar
[19] Tulsyan B, Balasubramanian K, Sujith R I 2009 Combust. Sci. Technol. 181 457
Google Scholar
[20] Matveev K I. 2003 ASME 2003 International Mechanical Engineering Congress and Exposition Washington, DC, November 15−21, 2003 p119
[21] Nair V, Sujith R I 2015 Proc. Combust. Inst. 35 3193
Google Scholar
[22] Seshadri A, Nair V, Sujith R I 2016 Combust. Theor. Model. 20 441
Google Scholar
[23] Singaravelu B, Mariappan S 2016 J. Fluid Mech. 801 597
Google Scholar
[24] Singaravelu B, Mariappan S 2017 Fifteenth Asian Congress of Fluid Mechanics Kuching, November 21–23, 2017 p12
[25] Chakravarthy S R, Sivakumar R, Shreenivasan O J 2007 Sadhana 32 145
Google Scholar
[26] Dotson K W, Koshigoe S, Pace K K 1997 J. Propul. Power 13 197
Google Scholar
-
图 1 带后向台阶的燃烧室简化模型
Figure 1. The simplified model of combustor with backward facing step.
图 3 相空间重构后的相图及庞加莱截面
Figure 3. Phase diagram after phase space reconstruction and Poincaré section.
图 4 不同初始扰动下压力比的初始时间序列
Figure 4. Initial time series of pressure ratios under different initial disturbances.
图 5 不同
${u_0}$ 下的压力比的最大值和最小值Figure 5. Maximum and minimum pressure ratios at different
${u_0}$ .
图 7 O1, O2, O3, O4, O5, O6的
$p'/{p_0}$ 时间序列 (a) u0 = 5.50; (b) u0 = 6.25; (c) u0 = 7.50; (d) u0 = 9.50; (e) u0 = 12.75; (f) u0 = 19.25Figure 7.
$p'/{p_0}$ time series of O1, O2, O3, O4, O5, O6: (a) u0 = 5.50; (b) u0 = 6.25; (c) u0 = 7.50; (d) u0 = 9.50; (e) u0 = 12.75; (f) u0 = 19.25
图 8 S1, S2, S3, S4, S5, O7的
$p'/{p_0}$ 时间序列Figure 8.
$p'/{p_0}$ time series of S1, S2, S3, S4, S5, O7.
图 9 涡声锁频
Figure 9. Vortex-acoustic frequency locking.
图 10
${f_{\rm{p}}}$ 与${f_{\rm{s}}}$ 的关系及${f_{\rm{p}}}/{f_{\rm{s}}}$ 随${u_0}$ 的变化图Figure 10. The relationship between
${f_{\rm{p}}}$ and${f_{\rm{s}}}$ and the change of${f_{\rm{p}}}/{f_{\rm{s}}}$ with${u_0}$ .
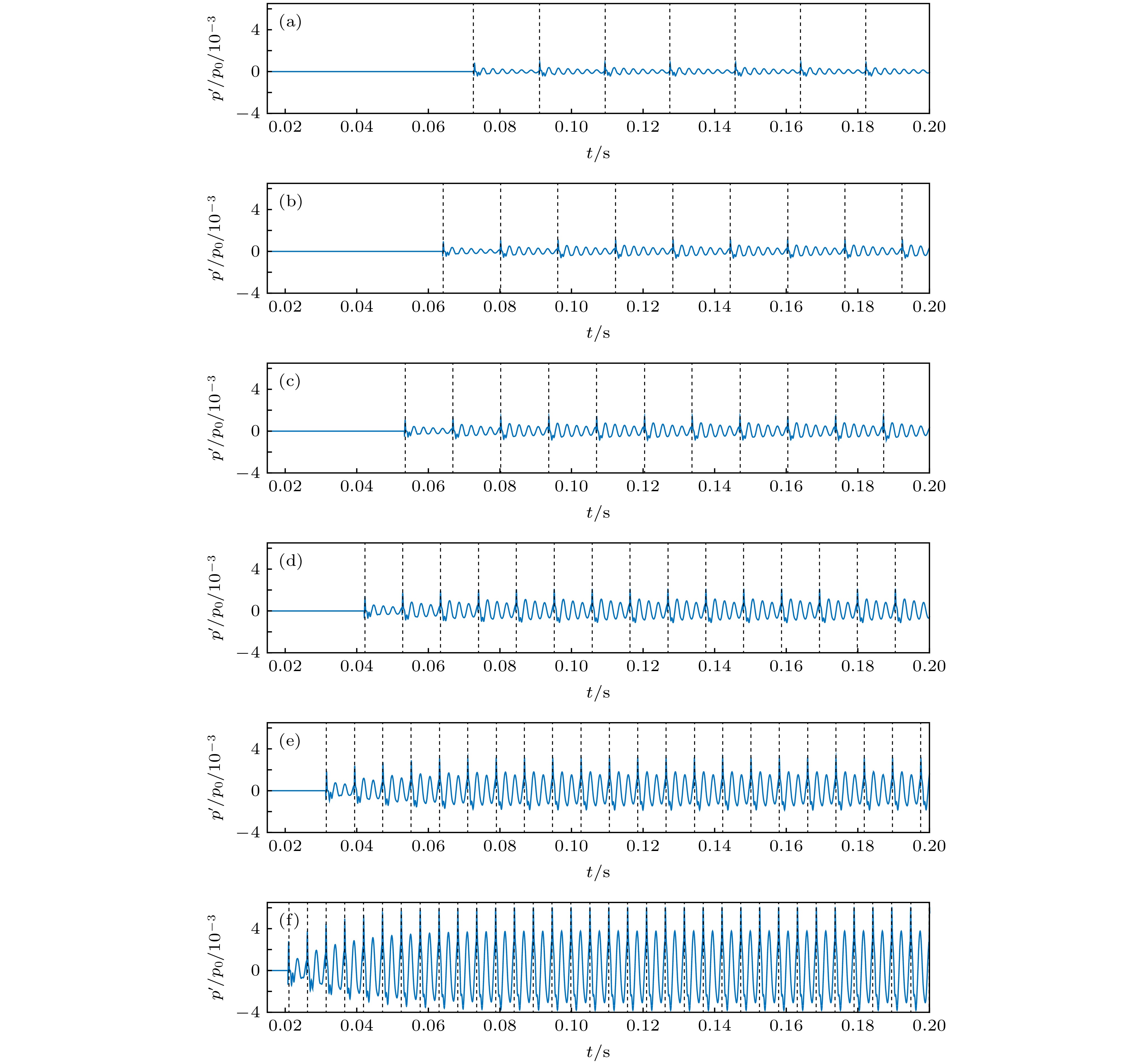
图 11 6个不同频率比下的
$u'$ -$p'/{p_0}$ 相图 (a) fs/fp = 0.1430; (b) fs/fp = 0.1669; (c) fs/fp = 0.2003; (d) fs/fp = 0.2500; (e) fs/fp = 0.3330; (f) fs/fp = 0.4999Figure 11.
$u'$ -$p'/{p_0}$ phase diagram at six different frequency ratios: (a) fs/fp = 0.1430; (b) fs/fp = 0.1669; (c) fs/fp = 0.2003; (d) fs/fp = 0.2500; (e) fs/fp = 0.3330; (f) fs/fp = 0.4999. -
[1] Zinn B T, Lieuwen T C 2005 Combustion IInstabilities: Basic Concepts 210 3
[2] Annaswamy A M, Ghoniem A F 2002 IEEE Control Syst. Mag. 22 37
Google Scholar
[3] Balasubramanian K, Sujith R I 2008 Phys. Fluids 20 44
[4] Subramanian P, Mariappan S, Sujith R I, Wahi P 2010 Int. J. Spray Combust. 2 325
Google Scholar
[5] 党南南, 张正元, 张家忠 2018 物理学报 67 134301
Google Scholar
Dang N N, Zhang Z Y, Zhang J Z 2018 Acta Phys. Sin. 67 134301
Google Scholar
[6] Rogers D E 1956 Jet Propul. 26 456
Google Scholar
[7] Hegde U G, Reuter D, Daniel B R, Zinn B T 1987 Combust. Sci. Technol. 55 125
Google Scholar
[8] Poinsot T J, Trouve A C, Veynante D P, Candel S M, Esposito E J 1987 J. Fluid Mech. 177 265
Google Scholar
[9] Sterling J D, Zukoski E E 1991 Combust. Sci. Technol. 77 225
Google Scholar
[10] Cohen J, Anderson T 1996 34th Aerospace Sciences Meeting and Exhibit Reno, January 15−18, 1996 p819
[11] Speth R, Altay H, Hudgins D, Annaswamy A, Ghoniem A 2008 46th AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 7–10, 2008 p1053
[12] Bauwens L, Daily J W 1992 J. Propul. Power 8 264
Google Scholar
[13] Najm H N, Ghoniem 1993 Combust. Sci. Technol. 94 259
Google Scholar
[14] Menon S, Jou W H 1991 Combust. Sci. Technol. 75 53
Google Scholar
[15] Angelberger C, Veynante D, Egolfopoulos F 2000 Flow Turbul. Combust. 65 205
Google Scholar
[16] Qin F, He G Q, Li J, Liu P J 2007 43rd AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit Cincinnati, OH, July 8–11, 2007 p5748
[17] 万少文, 何国强, 石磊 2011 固体火箭技术 34 32
Google Scholar
Wan S W, He G Q, Shi L 2011 Journal of Solid Rocket Technology 34 32
Google Scholar
[18] Matveev K I, Culick F E C 2003 Combust. Sci. Technol. 175 1059
Google Scholar
[19] Tulsyan B, Balasubramanian K, Sujith R I 2009 Combust. Sci. Technol. 181 457
Google Scholar
[20] Matveev K I. 2003 ASME 2003 International Mechanical Engineering Congress and Exposition Washington, DC, November 15−21, 2003 p119
[21] Nair V, Sujith R I 2015 Proc. Combust. Inst. 35 3193
Google Scholar
[22] Seshadri A, Nair V, Sujith R I 2016 Combust. Theor. Model. 20 441
Google Scholar
[23] Singaravelu B, Mariappan S 2016 J. Fluid Mech. 801 597
Google Scholar
[24] Singaravelu B, Mariappan S 2017 Fifteenth Asian Congress of Fluid Mechanics Kuching, November 21–23, 2017 p12
[25] Chakravarthy S R, Sivakumar R, Shreenivasan O J 2007 Sadhana 32 145
Google Scholar
[26] Dotson K W, Koshigoe S, Pace K K 1997 J. Propul. Power 13 197
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9003
- PDF Downloads: 79
- Cited By: 0
