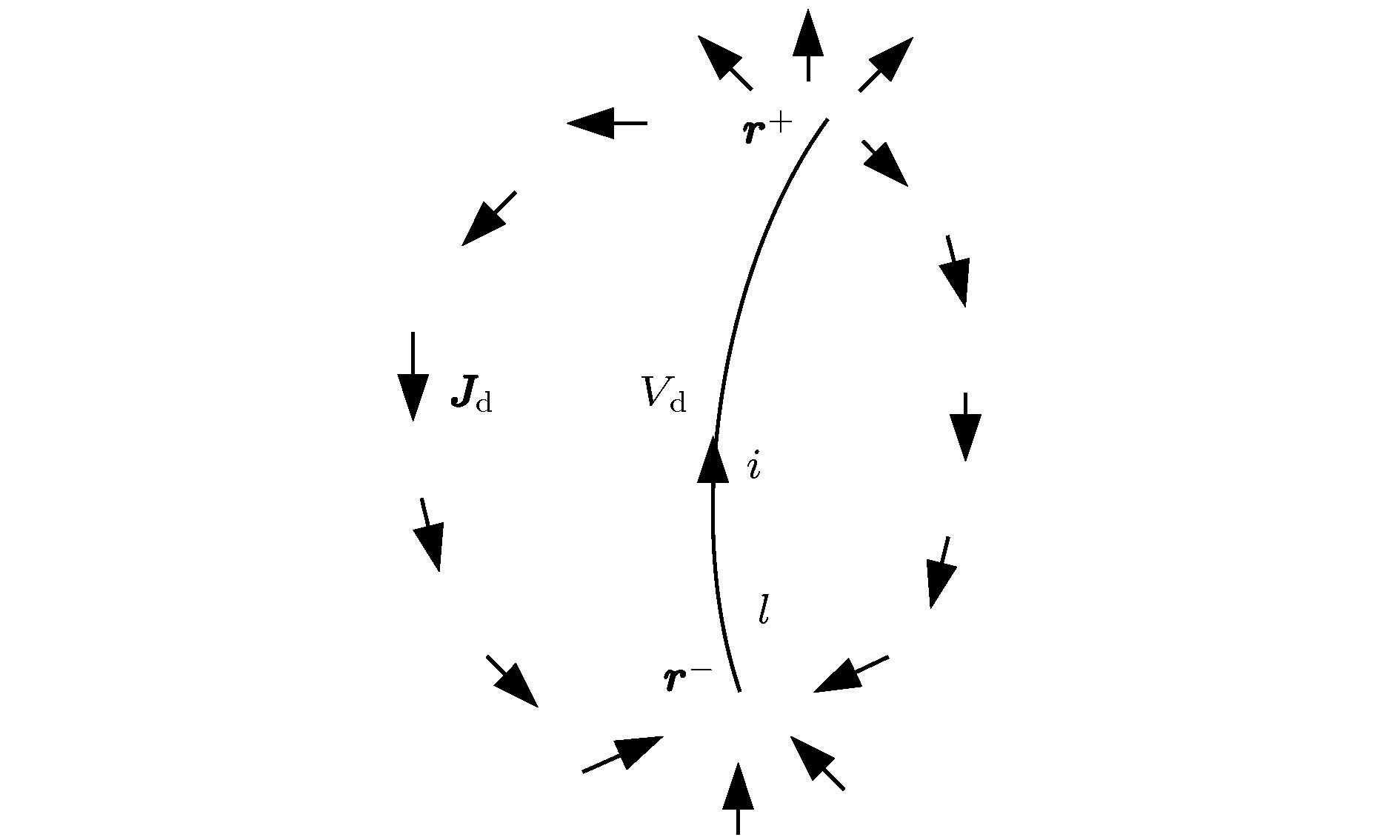
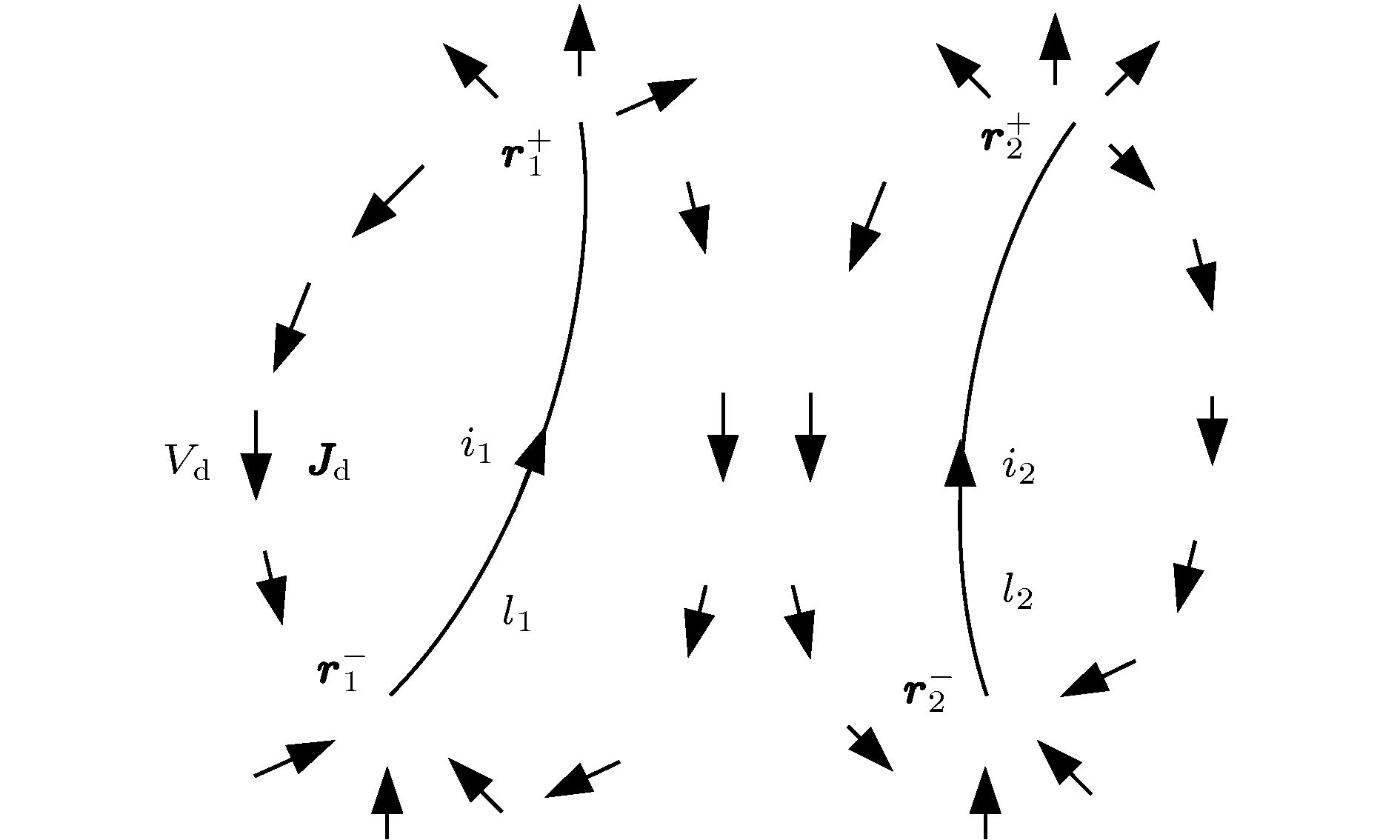
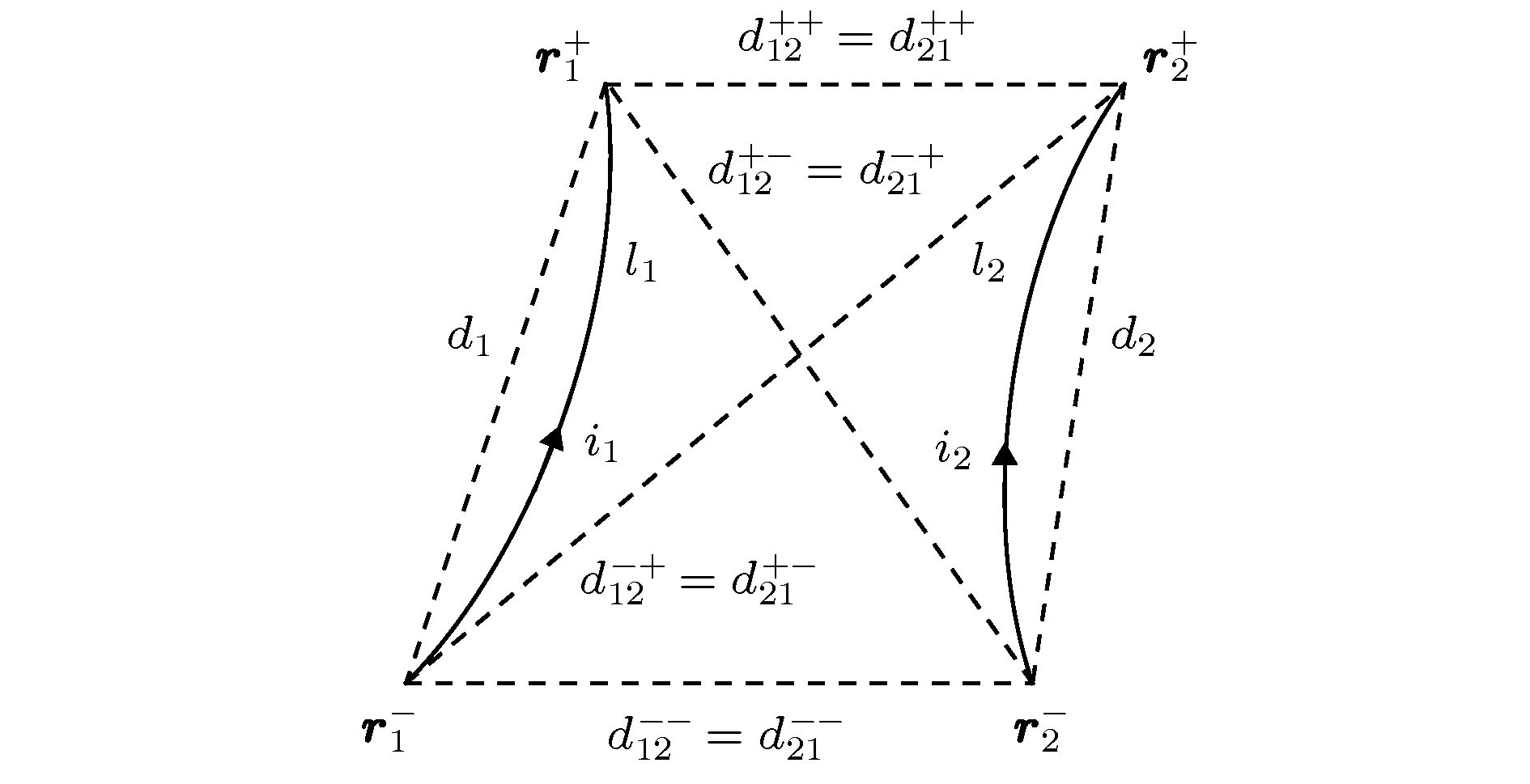
-
Traditional current-carrying model of filament conductor segment is the basic model for analyzing the magnetic field in a closed conductor loop. Although it does not satisfy the law of current continuity, it is still suitable for analyzing the magnetic field in the closed conductor loop. However, for the current distribution problem of some local multi-branch parallel-connection conductor segments in a closed conductor loop, the traditional model cannot fully reflect the interaction between magnetic fields of the local multi-branch parallel-connection conductor segments. For this reason, the displacement current model proposed in the existing literature satisfies the law of current continuity and solves the above problem well. But, there remain some problems to be solved, such as incomplete theory, inconsistency and complex formulae in the existing literature. In this paper, a conductive current-carrying model of filament conductor segment is proposed, which ensures current continuity inside, outside, and on two terminals of the filament conductor segment. The differential equation of total magnetic field with more profound physical connotation and the formulae of vector magnetic potential are derived in detail. Further, the formulae for calculating magnetic field energy and inductance of the conductive current-carrying model of filament conductor segment are proposed, which greatly reduces the computational complexity and makes up for the shortcoming of model in the existing literature. An example given in this paper verifies the correctness of the above theory and formulae.
-
Keywords:
- filament conductor segment /
- current continuity /
- magnetic field /
- inductance
[1] Stratton J A 1941 Electromagnetic Theory (New York: McGraw-Hill Book Company) p232
[2] Ogura K, Steinmetz C P 1907 Phys. Rev. 25 184
[3] Rosa E B 1908 Bulletin of the Bureau of Standards 4 301
Google Scholar
[4] Grover F W 1947 Inductance Calculations: Working Formulas and Tables (New York: D. Van Nostrand Company Inc.) pp31−247
[5] Kaiser K L 2005 Electromagnetic Compatibility Handbook (New York: CRC Press) Chapter 15 pp168−204
[6] Paul C R 2011 Inductance: Loop and Partial (New York: John Wiley & Sons) pp117−306
[7] Ni C W, Zhao Z B, Cui X 2018 IEEE Trans. Electromagn. Compat. 60 803
Google Scholar
[8] Wakeman F, Li G, Golland A 2005 Proceedings of PCIM Europe Nuremberg, Germany, June 7−9, 2005 p137
[9] Ruehli A E 1972 IBM J. Res. Develop. 16 470
Google Scholar
[10] Holloway C L, Kuester E F, Ruehli A E, Antonini G 2013 IEEE Trans. Electromagn. Compat. 55 600
Google Scholar
[11] Kamon M, Tsuk M, White J 1994 IEEE Trans. Microw. Theory Tech. 42 1750
Google Scholar
[12] FastHenry Package http://www.fastfieldsolvers.com/links.htm [2019-10-12]
[13] Ruehli A E, Antonini G, Esch J, Ekman J, Mayo A, Orlandi A 2003 IEEE Trans. Electromagn. Compat. 45 167
Google Scholar
[14] Yu W J, Yan C H, Wang Z Y 2007 Eng. Anal. Boundary Elem. 31 812
Google Scholar
[15] Holloway C L, Kuester E F 2009 IEEE Trans. Electromagn. Compat. 51 338
Google Scholar
[16] Antonini G, Orlandi A, Paul C R 1999 IEEE Trans. Microw. Theory Tech. 47 979
Google Scholar
[17] Ni C W, Zhao Z B, Cui X 2018 IEEE Trans. Magn. 53 1
Google Scholar
[18] Kalhor H A 1988 IEEE Trans. Educ. 31 236
Google Scholar
[19] 倪筹帷 2018 博士学位论文 (北京: 华北电力大学)
Ni C W 2018 Ph. D. Dissertation (Beijing: North China Electric Power University) (in Chinese)
[20] Kalhor H A 1990 IEEE Trans. Educ. 33 2365
Google Scholar
[21] 倪筹帷, 赵志斌, 崔翔 2017 中国电机工程学报 37 5181
Google Scholar
Ni C W, Zhao Z B, Cui X 2017 Proc. CSEE 37 5181
Google Scholar
-
图 1 传统的载流细导体段模型 (a) 单个载流细导体段; (b) 两个载流细导体段
Figure 1. Classical current models of filament conductor segments: (a) One filament conductor segment; (b) two filament conductor segments.
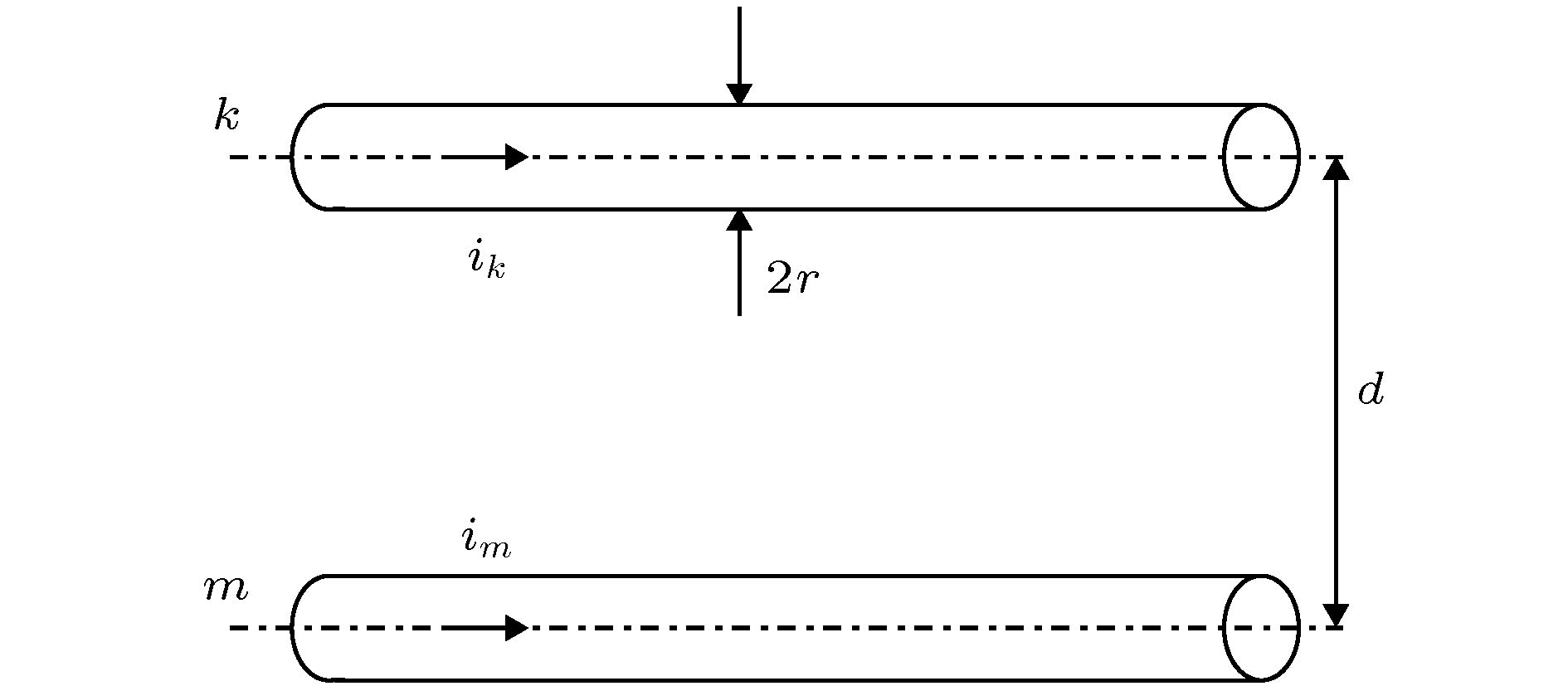
图 2 多导体段并联及其等效电路 (a) 三导体段并联[7]; (b) 压接型IGBT器件内部多凸台芯片并联[8]; (c) 多导体段并联的等效电路
Figure 2. Multiconductor parallel connection and its equivalent circuit: (a) Three conductors in parallel connection[7]; (b) multi-protrusion chips parallel connection in Press-Pack IGBTs[8]; (c) equivalent circuit for multiconductor parallel connection.
图 3 载流细导体段的传导电流模型
Figure 3. Conductive current model of filament conductor segment.
图 4 两根细导体段
Figure 4. Two filament conductor segments.
图 5 两根细导体段不同端点之间的距离
Figure 5. Distances between different terminals of two filament conductor segments.
-
[1] Stratton J A 1941 Electromagnetic Theory (New York: McGraw-Hill Book Company) p232
[2] Ogura K, Steinmetz C P 1907 Phys. Rev. 25 184
[3] Rosa E B 1908 Bulletin of the Bureau of Standards 4 301
Google Scholar
[4] Grover F W 1947 Inductance Calculations: Working Formulas and Tables (New York: D. Van Nostrand Company Inc.) pp31−247
[5] Kaiser K L 2005 Electromagnetic Compatibility Handbook (New York: CRC Press) Chapter 15 pp168−204
[6] Paul C R 2011 Inductance: Loop and Partial (New York: John Wiley & Sons) pp117−306
[7] Ni C W, Zhao Z B, Cui X 2018 IEEE Trans. Electromagn. Compat. 60 803
Google Scholar
[8] Wakeman F, Li G, Golland A 2005 Proceedings of PCIM Europe Nuremberg, Germany, June 7−9, 2005 p137
[9] Ruehli A E 1972 IBM J. Res. Develop. 16 470
Google Scholar
[10] Holloway C L, Kuester E F, Ruehli A E, Antonini G 2013 IEEE Trans. Electromagn. Compat. 55 600
Google Scholar
[11] Kamon M, Tsuk M, White J 1994 IEEE Trans. Microw. Theory Tech. 42 1750
Google Scholar
[12] FastHenry Package http://www.fastfieldsolvers.com/links.htm [2019-10-12]
[13] Ruehli A E, Antonini G, Esch J, Ekman J, Mayo A, Orlandi A 2003 IEEE Trans. Electromagn. Compat. 45 167
Google Scholar
[14] Yu W J, Yan C H, Wang Z Y 2007 Eng. Anal. Boundary Elem. 31 812
Google Scholar
[15] Holloway C L, Kuester E F 2009 IEEE Trans. Electromagn. Compat. 51 338
Google Scholar
[16] Antonini G, Orlandi A, Paul C R 1999 IEEE Trans. Microw. Theory Tech. 47 979
Google Scholar
[17] Ni C W, Zhao Z B, Cui X 2018 IEEE Trans. Magn. 53 1
Google Scholar
[18] Kalhor H A 1988 IEEE Trans. Educ. 31 236
Google Scholar
[19] 倪筹帷 2018 博士学位论文 (北京: 华北电力大学)
Ni C W 2018 Ph. D. Dissertation (Beijing: North China Electric Power University) (in Chinese)
[20] Kalhor H A 1990 IEEE Trans. Educ. 33 2365
Google Scholar
[21] 倪筹帷, 赵志斌, 崔翔 2017 中国电机工程学报 37 5181
Google Scholar
Ni C W, Zhao Z B, Cui X 2017 Proc. CSEE 37 5181
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9168
- PDF Downloads: 95
- Cited By: 0
