-
Periodic forcing of pattern-forming systems is always a research hot spot in the field of pattern formation since it is one of the most effective methods of controlling patterns. In reality, most of the pattern-forming systems are the multilayered systems, in which each layer is a reaction-diffusion system coupled to adjacent layers. However, few researches on this issue have been conducted in the multilayered systems and their responses to the periodic forcing have not yet been well understood. In this work, the influences of the spatial periodic forcing on the Turing patterns in two linearly coupled layers described by the Brusselator (Bru) model and the Lengyel-Epstein (LE) model respectively have been investigated by introducing a spatial periodic forcing into the LE layer. It is found that the subcritical Turing mode in the LE layer can be excited as long as one of the external spatial forcing and the supercritical Turing mode (referred to as internal forcing mode) of the Bru layer is a longer wave mode. These three modes interact together and give rise to complex patterns with three different spatial scales. If both the spatial forcing mode and the internal forcing mode are the short wave modes, the subcritical Turing mode in the LE layer cannot be excited. But the superlattice pattern can also be generated when the spatial resonance is satisfied. When the eigenmode of the LE layer is supercritical, a simple and robust hexagon pattern with its characteristic wavelength appears and responds to the spatial forcing only when the forcing intensity is large enough. It is found that the wave number of forcing has a powerful influence on the spatial symmetry of patterns.
-
Keywords:
- two-layer reaction-diffusion system /
- spatial periodic forcing /
- Turing patterns /
- space resonance
[1] Yochelis A, Gilad E, Nishiura Y, Silber M, Uecker H 2021 Physica D 415 132769
Google Scholar
[2] Sam E M, Hayase Y, Auernhammer G, Vollmer D 2011 Phys. Chem. Chem. Phys. 13 13333
Google Scholar
[3] Perinet N, Juric D, Tuckerman L S 2012 Phys. Rev. Lett. 109 164501
Google Scholar
[4] Alarcón H, Muñoz M H, Perinet N, Mujica N, Gutierrez P, Gordillo L 2020 Phys. Rev. Lett. 125 254505
Google Scholar
[5] Foster J E, Kovach Y E, Lai J, Garcia M C 2020 Plasma Sources Sci. T. 29 034004
Google Scholar
[6] Brauns F, Weyer H, Halatek J, Yoon J, Frey E 2021 Phys. Rev. Lett. 126 104101
Google Scholar
[7] Turing A M 1952 Phil. Trans. R. Soc. B 237 37
Google Scholar
[8] Fuseya Y, Katsuno H, Behnia K, Kapitulnik A 2021 Nat. Phys. 17 1031
Google Scholar
[9] Haas P A, Goldstein R E 2021 Phys. Rev. Lett. 126 238101
Google Scholar
[10] Mau Y, Hagberg A, Meron E 2012 Phys. Rev. Lett. 109 034102
Google Scholar
[11] Mau Y, Haim L, Hagberg A, Meron E 2013 Phys. Rev. E. 88 032917
Google Scholar
[12] Manor R, Hagberg A, Meron E 2009 New J. Phys. 11 063016
Google Scholar
[13] Dolnik M, Berenstein I, Zhabotinsky A M, Epstein I R 2001 Phys. Rev. Lett. 87 238301
Google Scholar
[14] Berenstein I, Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2003 Phys. Rev. Lett. 91 058302
Google Scholar
[15] Dolnik M, Jr. Bánsági T, Ansari S, Valent I, Epstein I. R 2011 Phys. Chem. Chem. Phys. 13 12578
Google Scholar
[16] Berenstein I, Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2005 J. Phys. Chem. A 109 5382
Google Scholar
[17] Nagao R, Epstein I R, Dolnik. M 2013 J. Phys. Chem. A 117 9120
Google Scholar
[18] Haim L, Hagberg A, Meron E 2015 Chaos 25 064307
Google Scholar
[19] Liu S, Yao C G, Wang X F, Zhao Q 2017 Physica A 467 184
Google Scholar
[20] Berenstein I, Munuzuri A P, Yang L F, Dolnik M, Zhabotinsk A M, Epstein I R 2008 Phys. Rev. E 78 025101
Google Scholar
[21] Barrio R A, Varea C, Aragón J L, Maini P K 1999 Bull. Math. Biol. 61 483
Google Scholar
[22] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[23] Paul S, Pal K, Ray D S 2020 Phys. Rev. E 102 052209
Google Scholar
[24] 李伟恒, 潘飞, 黎维新, 唐国宁 2015 物理学报 64 198201
Google Scholar
Li W H, Pan F, Li W X, Tang G N 2015 Acta Phys. Sin. 64 198201
Google Scholar
[25] Feng F, Yan J, Liu F C, He Y F 2016 Chin. Phys. B 25 104702
Google Scholar
[26] 刘富成, 刘雅慧, 周志向, 郭雪, 董梦菲 2020 物理学报 69 028201
Google Scholar
Liu F C, Liu Y H, Zhou Z X, Guo X, Dong M F 2020 Acta Phys. Sin. 69 028201
Google Scholar
[27] Miguez D G, Dolnik M, Epstein I R, Munuzuri A P 2011 Phys. Rev. E. 84 046210
Google Scholar
[28] 白婧, 关富荣, 唐国宁 2021 物理学报 70 170502
Google Scholar
Bai J, Guan F R, Tang G N 2021 Acta Phys. Sin. 70 170502
Google Scholar
[29] 李倩昀, 白婧, 唐国宁 2021 物理学报 70 098202
Google Scholar
Li Q Y, Bai J, Tang G N 2021 Acta Phys. Sin. 70 098202
Google Scholar
[30] 张秀芳, 马军, 徐莹, 任国栋 2021 物理学报 70 090502
Google Scholar
Zhang X F, Ma J, Xu Y, Ren G D 2021 Acta Phys. Sin. 70 090502
Google Scholar
[31] Wang Q, Ning W J, Dai D, Zhang Y H 2019 Plasma Process. Polym. 17 1900182
Google Scholar
[32] Sinclair J, Walhout M 2012 Phys. Rev. Lett. 108 035005
Google Scholar
[33] Fan W L, Hou X H, Tian M, Gao K Y, He Y F, Yang Y X, Liu Q, Yao J F, Liu F C, Yuan C X 2022 Plasma Sci. Technol. 24 015402
Google Scholar
[34] Fan W L, Sheng Z M, Dang W, Liang Y Q, Gao K Y, Dong L F 2019 Phys. Rev. Appl. 11 064057
Google Scholar
[35] 刘雅慧, 董梦菲, 刘富成, 田淼, 王硕, 范伟丽 2021 物理学报 70 158201
Google Scholar
Liu Y H, Dong M F, Liu F C, Tian M, Wang S, Fan W L 2021 Acta Phys. Sin. 70 158201
Google Scholar
[36] Fan W L, Liu C Y, Gao K Y, Liang Y Q, Liu F C 2021 Phys. Lett. A 396 127223
Google Scholar
[37] 白占国, 刘富成, 董丽芳 2015 物理学报 64 210505
Google Scholar
Bai Z G, Liu F C, Dong L F 2015 Acta Phys. Sin. 64 210505
Google Scholar
[38] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2002 Phys. Rev. Lett. 88 208303
Google Scholar
-
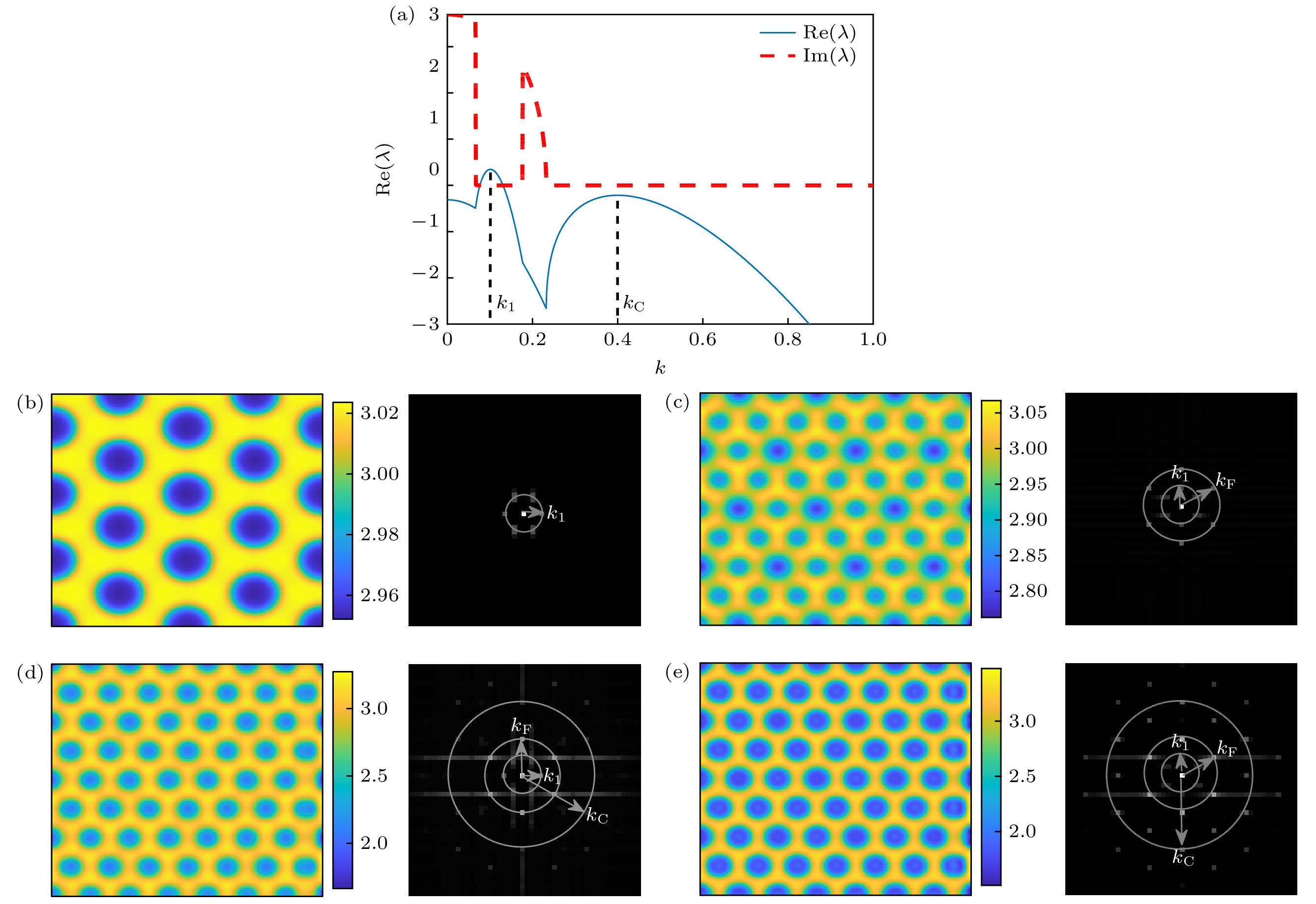
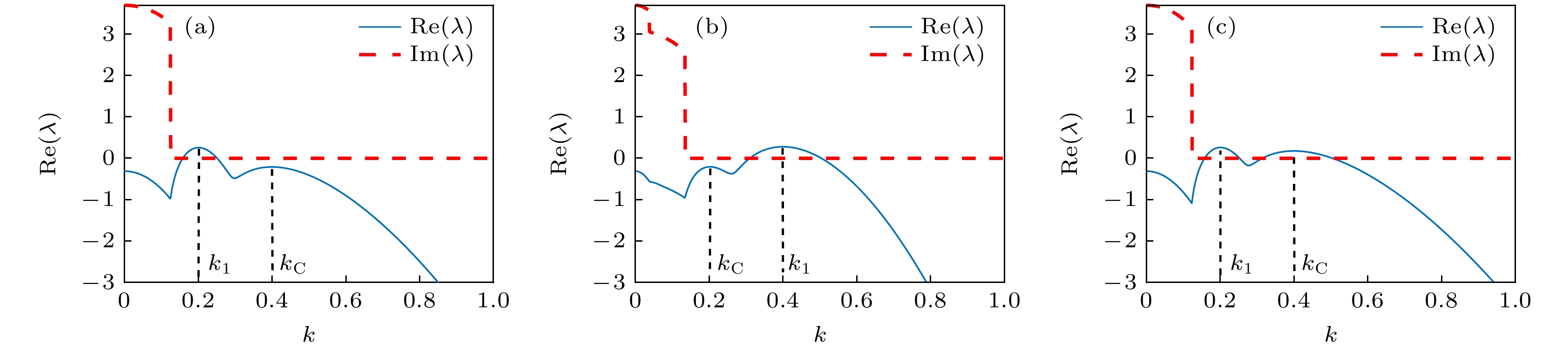
图 1 不同图灵模类型的双层耦合系统的色散关系图 (a) 类型I (
$ {D_{{u_1}}} = 50 $ ,$ {D_{{v_1}}} = 127 $ ,$ {D_{{u_2}}} = 6.6 $ ,$ {D_{{v_2}}} = 81 $ ,$ \alpha = 0.1 $ ); (b) 类型II ($ {D_{{u_1}}} = 12.5 $ ,$ {D_{{v_1}}} = 32 $ ,$ {D_{{u_2}}} = 26.5 $ ,$ {D_{{v_2}}} = 320 $ ,$ \alpha = 0.1 $ ); (c) 类型III ($ {D_{{u_1}}} = 50 $ ,$ {D_{{v_1}}} = 127 $ ,$ {D_{{u_2}}} = 5.5 $ ,$ {D_{{v_2}}} = 98 $ ,$ \alpha = 0.1 $ )Figure 1. Dispersion curves of two-layer coupled systems with different Turing mode types: (a) Type I (
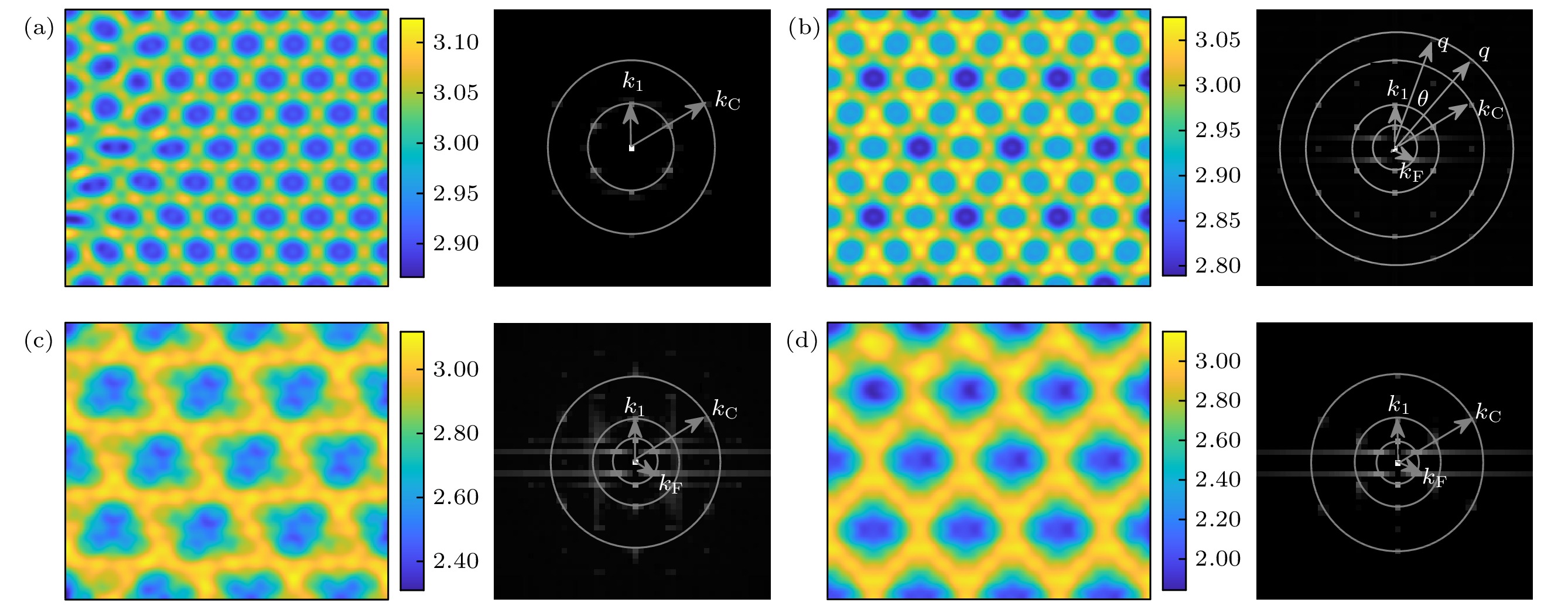
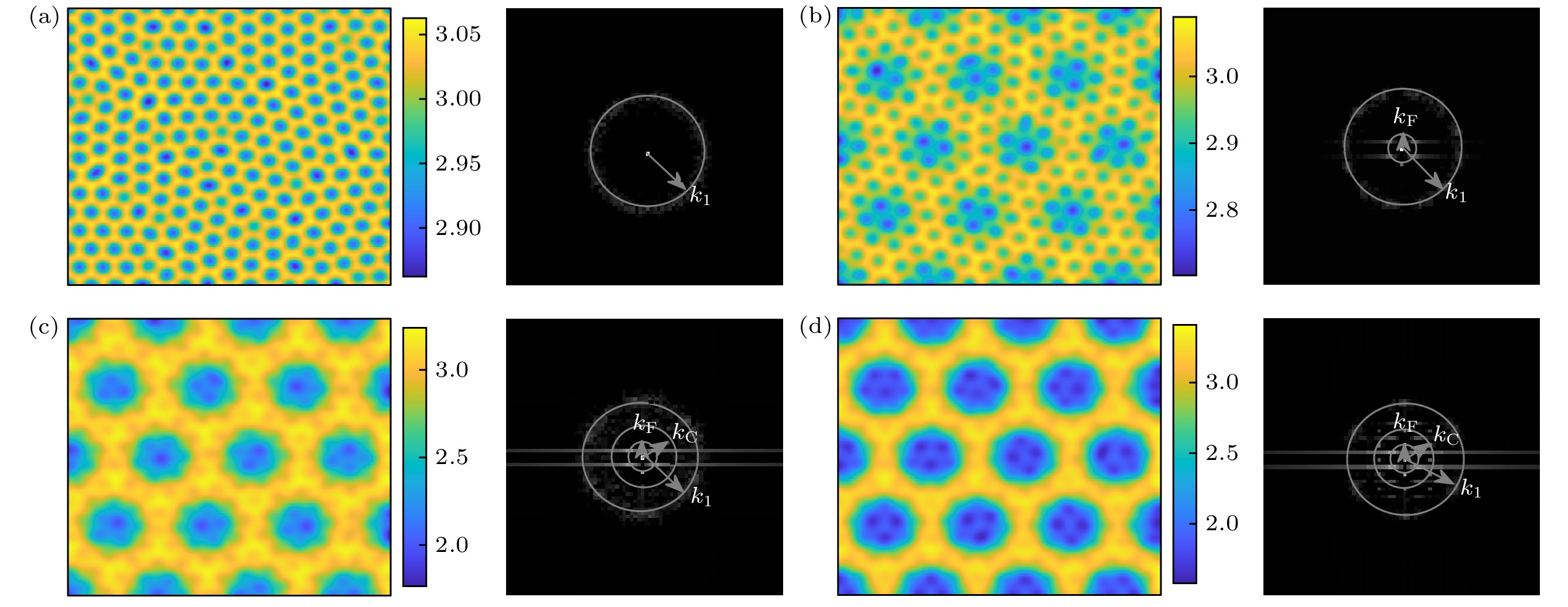
$ {D_{{u_1}}} = 50 $ ,$ {D_{{v_1}}} = 127 $ ,$ {D_{{u_2}}} = 6.6 $ ,$ {D_{{v_2}}} = 81 $ ,$ \alpha = 0.1 $ ); (b) type II ($ {D_{{u_1}}} = 12.5 $ ,$ {D_{{v_1}}} = 32 $ ,$ {D_{{u_2}}} = 26.5 $ ,$ {D_{{v_2}}} = 320 $ ,$ \alpha = 0.1 $ ); (c) type III ($ {D_{{u_1}}} = 50 $ ,$ {D_{{v_1}}} = 127 $ ,$ {D_{{u_2}}} = 5.5 $ ,$ {D_{{v_2}}} = 98 $ ,$ \alpha = 0.1 $ ).
图 2 类型I下不同驱动强度的图灵斑图及其傅里叶频谱图 (a) 超六边形斑图,
$ {w_0} = 0 $ ; (b) 雪花斑图I,$ {w_0} = 0.1 $ ; (c) 菱形网格斑图I,$ {w_0} = 0.5 $ ; (d) 菱形网格斑图II,$ {w_0} = 1.0 $ (超临界图灵模$ {k_1}=0.2 $ , 次临界本征模$ {k_{\rm{C}}}=0.4 $ , 驱动的波数$ {k_{\rm{F}}}=0.1 $ ;$N =256$ ,$ \Delta x = \Delta y = 1 $ )Figure 2. Patterns and Fourier spectrum with different forcing intensity in type I: (a) Super-hexagon pattern,
$ {w_0} = 0 $ ; (b) snowflake pattern I,$ {w_0} = 0.1 $ ; (c) rhombus mash pattern I,$ {w_0} = 0.5 $ ; (d) rhombus mash pattern II,$ {w_0} = 1.0 $ (Supercritical Turing mode$ {k_1}=0.2 $ , subcritical eigenmode$ {k_{\rm{C}}}=0.4 $ , wavenumber of forcing$ {k_{\rm{F}}}=0.1 $ ;$N = 256$ ,$ \Delta x = \Delta y = 1 $ )
图 3 类型I下不同驱动波数的斑图及其傅里叶频谱图 (a) 超六边形斑图,
$ {k_{\rm{F}}}=0.2 $ ; (b) 简单六边形蜂窝斑图,$ {k_{\rm{F}}}=0.4 $ ; (c) 六边形网格斑图I,$ {k_{\rm{F}}}=0.6 $ ; (d) 六边形网格斑图II,$ {k_{\rm{F}}}=0.8 $ (超临界图灵模$ {k_1}=0.2 $ , 次临界本征模$ {k_{\rm{C}}}=0.4 $ , 驱动的强度恒为$ {w_0} = 0.1 $ ,$N = 256$ ,$ \Delta x = \Delta y = 1 $ )Figure 3. Patterns and Fourier spectrum with different forcing wavenumber in type I: (a) Super-hexagon pattern,
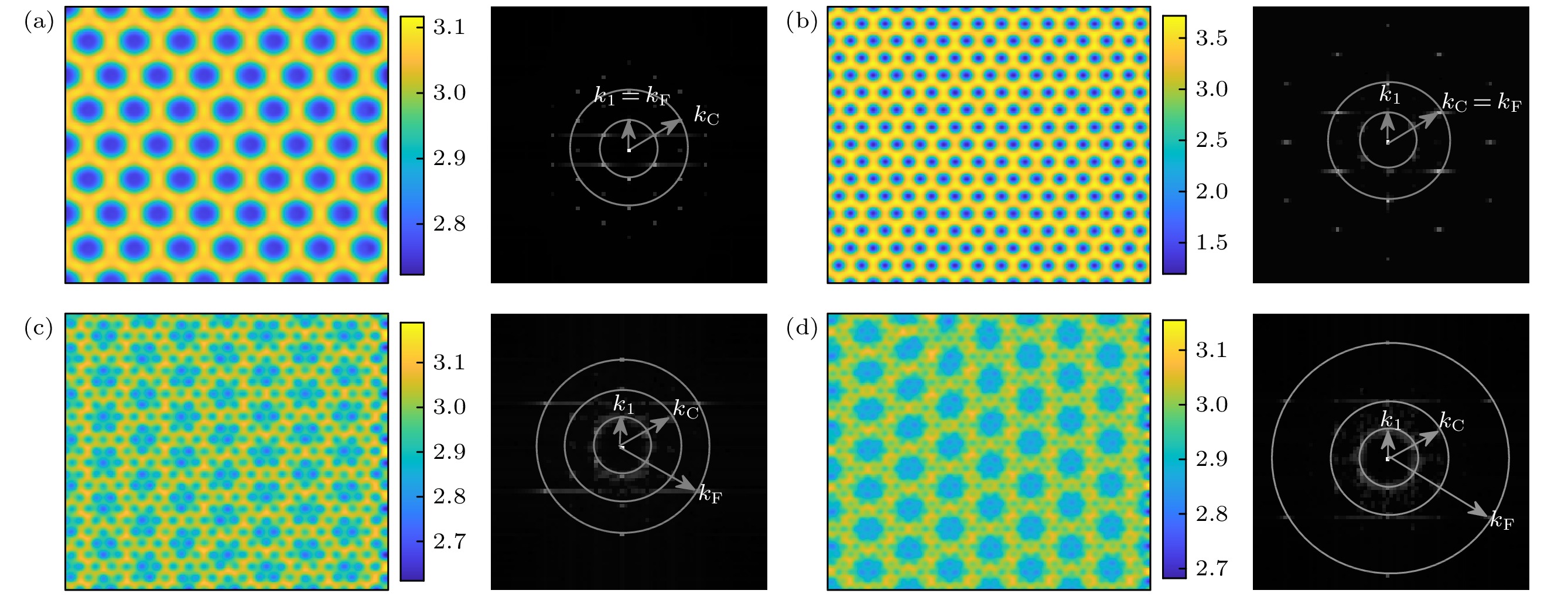
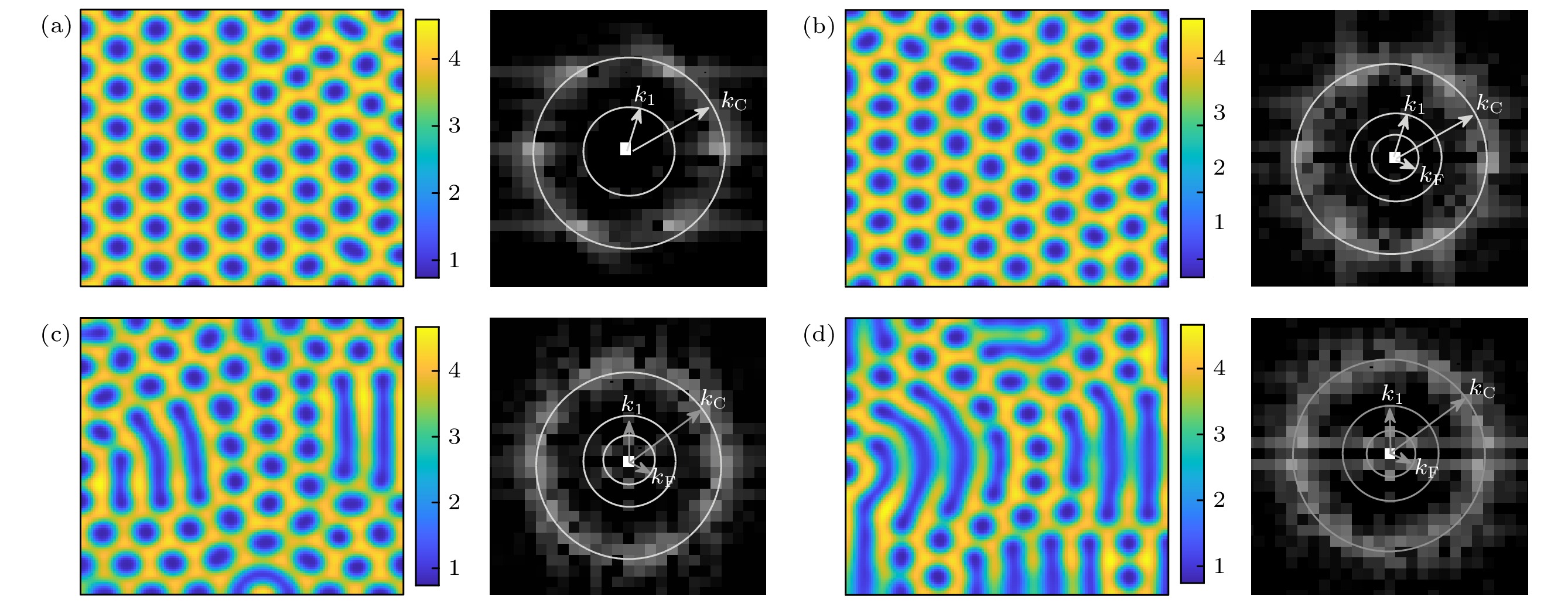
$ {k_{\rm{F}}}=0.2 $ ; (b) simple hexagonal honeycomb pattern,$ {k_{\rm{F}}}=0.4 $ ; (c) hexagonal mash pattern I,$ {k_{\rm{F}}}=0.6 $ ; (d) hexagonal mash pattern II,$ {k_{\rm{F}}}=0.8 $ (Supercritical Turing mode$ {k_1}=0.2 $ , subcritical eigenmode$ {k_{\rm{C}}}=0.4 $ , forcing intensity$ {w_0} = 0.1 $ ,$N = 256$ ,$ \Delta x = \Delta y = 1 $ )
图 4 波数反转后不同驱动强度下的斑图及其傅里叶频谱图 (a) 色散关系图(
$ {k_1}:{k_{\text{C}}} = 1:4 $ ,$ {D_{{u_1}}} = 195 $ ,$ {D_{{v_1}}} = 510 $ ,$ {D_{{u_2}}} = 6.6 $ ,$ {D_{{v_2}}} = 81 $ ,$ \alpha = 0.1 $ ); (b) 简单六边形蜂窝斑图,$ {w_0} = 0 $ ; (c) 雪花斑图II,$ {w_0} = 0.1 $ ; (d) 简单六边形蜂窝斑图,$ {w_0} = 0.6 $ ; (e) 六边形白眼斑图,$ {w_0} = 1.0 $ (驱动的波数$ {k_{\rm{F}}} = 0.2 $ ;$N = 256$ ,$ \Delta x = \Delta y = 1 $ )Figure 4. Patterns and Fourier spectrum of different forcing intensity after wavenumber inversion: (a) Dispersion curve (
${k_1}:{k_{\text{C}}} = $ $ 1:4$ ,$ {D_{{u_1}}} = 195 $ ,$ {D_{{v_1}}} = 510 $ ,$ {D_{{u_2}}} = 6.6 $ ,$ {D_{{v_2}}} = 81 $ ,$ \alpha = 0.1 $ ); (b) simple hexagonal honeycomb pattern,$ {w_0} = 0 $ ; (c) snowflake pattern II,$ {w_0} = 0.1 $ ; (d) simple hexagonal honeycomb pattern,$ {w_0} = 0.6 $ ; (e) hexagonal white-eye pattern,$ {w_0} = 1.0 $ (Wavenumber of forcing$ {k_{\rm{F}}} = 0.2 $ ,$N = 256$ ,$ \Delta x = \Delta y = 1 $ )
图 5 类型II下不同短波驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,
$ {w_0} = 0 $ ; (b) 简单六边形蜂窝斑图,$ {w_0} = 0.1 $ ; (c) 六边形花瓣斑图I,$ {w_0} = 0.5 $ ; (d) 六边形花瓣斑图II,$ {w_0} = 1.0 $ (超临界图灵模$ {k_1}=0.4 $ , 次临界本征模$ {k_{\rm{C}}}=0.2 $ , 驱动的波数$ {k_{\rm{F}}}=0.8 $ ,$N = 128$ ,$ \Delta x = \Delta y = 0.5 $ )Figure 5. Patterns and Fourier spectrum of different short-wave forcing intensity in type II: (a) Simple hexagonal honeycomb pattern,
$ {w_0} = 0 $ ; (b) simple hexagonal honeycomb pattern,$ {w_0} = 0.1 $ ; (c) hexagonal petal pattern pattern I,$ {w_0} = 0.5 $ ; (d) hexagonal petal pattern pattern II;$ {w_0} = 1.0 $ (Supercritical Turing mode$ {k_1}=0.4 $ , subcritical eigenmode$ {k_{\rm{C}}}=0.2 $ , wavenumber of forcing$ {k_{\rm{F}}}=0.8 $ ,$N = 128$ ,$ \Delta x = \Delta y = 0.5 $ )
图 6 类型II下不同长波驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,
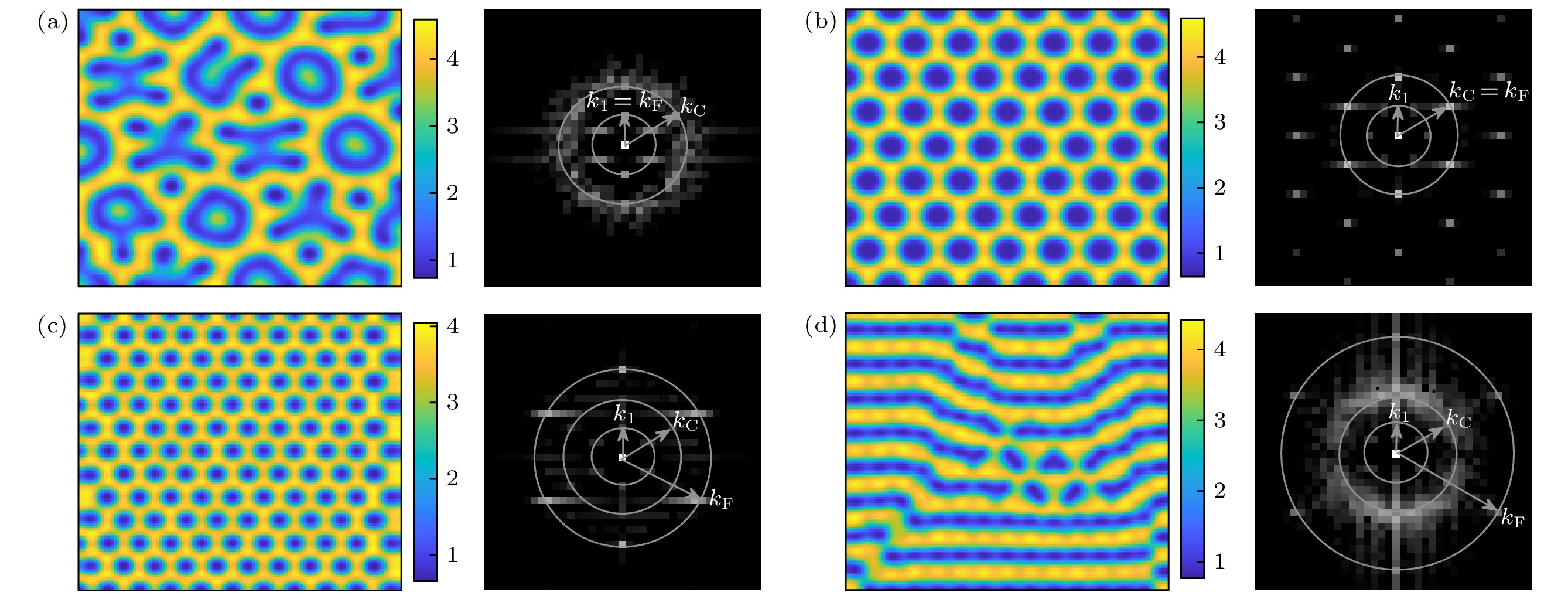
$ {w_0} = 0 $ ; (b) 简单六边形蜂窝斑图,$ {w_0} = 0.1 $ ; (c) 六边形蜂窝斑图,$ {w_0} = 0.6 $ ; (d) 黑眼六边形蜂窝斑图,$ {w_0} = 1.0 $ (超临界图灵模$ {k_1}=0.4 $ , 次临界本征模$ {k_{\rm{C}}}=0.2 $ , 驱动的波数$ {k_{\rm{F}}}=0.1 $ ,$N = 256$ ,$ \Delta x = \Delta y = 1 $ )Figure 6. Patterns and Fourier spectrum of different long-wave forcing intensity in type II: (a) Simple hexagonal honeycomb pattern,
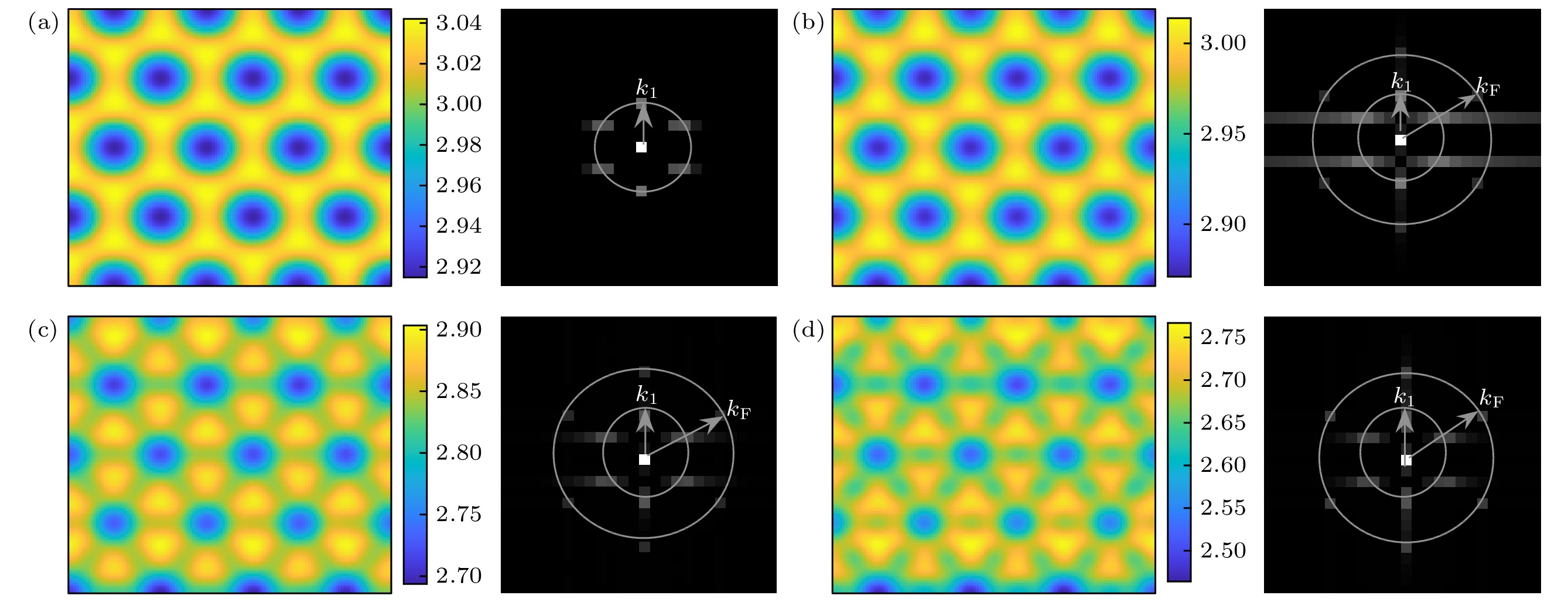
$ {w_0} = 0 $ ; (b) simple hexagonal honeycomb pattern,$ {w_0} = 0.1 $ ; (c) hexagonal honeycomb pattern,$ {w_0} = 0.6 $ ; (d) black-eye hexagonal honeycomb pattern,$ {w_0} = 1.0 $ (Supercritical Turing mode$ {k_1}=0.4 $ , subcritical eigenmode$ {k_{\rm{C}}}=0.2 $ , wavenumber of forcing$ {k_{\rm{F}}}=0.1 $ ,$N = 256$ ,$ \Delta x = \Delta y = 1 $ )
图 7 类型III下不同驱动强度的斑图及其傅里叶频谱图 (a) 简单六边形蜂窝斑图,
$ {w_0} = 0 $ ; (b) 简单六边形蜂窝斑图,$ {w_0} = 0.1 $ ; (c) 调制蜂窝斑图,$ {w_0} = 0.5 $ ; (d) 条纹与蜂窝六边形共存斑图,$ {w_0} = 1.0 $ (超临界图灵模$ {k_1}=0.2 $ , 超临界图灵模${k_{\rm C}} = 0.4$ , 驱动的波数${k_{\rm F}} = 0.1$ ;$N = 128$ ,$ \Delta x = \Delta y = 1 $ )Figure 7. Patterns and Fourier spectrum with different forcing intensity in type III: (a) Simple hexagonal honeycomb pattern,
$ {w_0} = 0 $ ; (b) simple hexagonal honeycomb pattern,$ {w_0} = 0.1 $ ; (c) modulated honeycomb pattern,$ {w_0} = 0.5 $ ; (d) coexistence of stripe and honeycomb hexagon,$ {w_0} = 1.0 $ (Supercritical Turing mode$ {k_1}=0.2 $ , supercritical Turing mode${k_{\rm C}} = 0.4$ , wavenumber of forcing${k_{\rm F}} = 0.1$ ,$N = 128$ ,$ \Delta x = \Delta y = 1 $ )
图 8 类型III下不同驱动波数的斑图及其傅里叶频谱图 (a) 复杂斑图,
$ {k_{\rm{F}}}=0.2 $ ; (b) 简单六边形蜂窝斑图,$ {k_{\rm{F}}}=0.4 $ ; (c) 简单六边形蜂窝斑图,$ {k_{\rm{F}}}=0.6 $ ; (d) 条纹斑图,$ {k_{\rm{F}}}=0.8 $ (超临界图灵模$ {k_1}=0.2 $ , 超临界图灵模${k_{\rm C}} = 0.4$ , 驱动的强度固定为$ {w_0} = 1.0 $ ,$N = 128$ ,$ \Delta x = \Delta y = 1 $ )Figure 8. Patterns and Fourier spectrum with different forcing wavenumber in type III: (a) Complex pattern,
$ {k_{\rm{F}}}=0.2 $ ; (b) simple hexagonal honeycomb pattern,$ {k_{\rm{F}}}=0.4 $ ; (c) simple hexagonal honeycomb pattern,$ {k_{\rm{F}}}=0.6 $ ; (d) stripe pattern,$ {k_{\rm{F}}}=0.8 $ (Supercritical Turing mode$ {k_1}=0.2 $ , supercritical Turing mode${k_{\rm C}} = 0.4$ , forcing intensity$ {w_0} = 1.0 $ ,$N = 128$ ,$ \Delta x = \Delta y = 1 $ ) -
[1] Yochelis A, Gilad E, Nishiura Y, Silber M, Uecker H 2021 Physica D 415 132769
Google Scholar
[2] Sam E M, Hayase Y, Auernhammer G, Vollmer D 2011 Phys. Chem. Chem. Phys. 13 13333
Google Scholar
[3] Perinet N, Juric D, Tuckerman L S 2012 Phys. Rev. Lett. 109 164501
Google Scholar
[4] Alarcón H, Muñoz M H, Perinet N, Mujica N, Gutierrez P, Gordillo L 2020 Phys. Rev. Lett. 125 254505
Google Scholar
[5] Foster J E, Kovach Y E, Lai J, Garcia M C 2020 Plasma Sources Sci. T. 29 034004
Google Scholar
[6] Brauns F, Weyer H, Halatek J, Yoon J, Frey E 2021 Phys. Rev. Lett. 126 104101
Google Scholar
[7] Turing A M 1952 Phil. Trans. R. Soc. B 237 37
Google Scholar
[8] Fuseya Y, Katsuno H, Behnia K, Kapitulnik A 2021 Nat. Phys. 17 1031
Google Scholar
[9] Haas P A, Goldstein R E 2021 Phys. Rev. Lett. 126 238101
Google Scholar
[10] Mau Y, Hagberg A, Meron E 2012 Phys. Rev. Lett. 109 034102
Google Scholar
[11] Mau Y, Haim L, Hagberg A, Meron E 2013 Phys. Rev. E. 88 032917
Google Scholar
[12] Manor R, Hagberg A, Meron E 2009 New J. Phys. 11 063016
Google Scholar
[13] Dolnik M, Berenstein I, Zhabotinsky A M, Epstein I R 2001 Phys. Rev. Lett. 87 238301
Google Scholar
[14] Berenstein I, Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2003 Phys. Rev. Lett. 91 058302
Google Scholar
[15] Dolnik M, Jr. Bánsági T, Ansari S, Valent I, Epstein I. R 2011 Phys. Chem. Chem. Phys. 13 12578
Google Scholar
[16] Berenstein I, Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2005 J. Phys. Chem. A 109 5382
Google Scholar
[17] Nagao R, Epstein I R, Dolnik. M 2013 J. Phys. Chem. A 117 9120
Google Scholar
[18] Haim L, Hagberg A, Meron E 2015 Chaos 25 064307
Google Scholar
[19] Liu S, Yao C G, Wang X F, Zhao Q 2017 Physica A 467 184
Google Scholar
[20] Berenstein I, Munuzuri A P, Yang L F, Dolnik M, Zhabotinsk A M, Epstein I R 2008 Phys. Rev. E 78 025101
Google Scholar
[21] Barrio R A, Varea C, Aragón J L, Maini P K 1999 Bull. Math. Biol. 61 483
Google Scholar
[22] Li J, Wang H L, Ouyang Q 2014 Chaos 24 023115
Google Scholar
[23] Paul S, Pal K, Ray D S 2020 Phys. Rev. E 102 052209
Google Scholar
[24] 李伟恒, 潘飞, 黎维新, 唐国宁 2015 物理学报 64 198201
Google Scholar
Li W H, Pan F, Li W X, Tang G N 2015 Acta Phys. Sin. 64 198201
Google Scholar
[25] Feng F, Yan J, Liu F C, He Y F 2016 Chin. Phys. B 25 104702
Google Scholar
[26] 刘富成, 刘雅慧, 周志向, 郭雪, 董梦菲 2020 物理学报 69 028201
Google Scholar
Liu F C, Liu Y H, Zhou Z X, Guo X, Dong M F 2020 Acta Phys. Sin. 69 028201
Google Scholar
[27] Miguez D G, Dolnik M, Epstein I R, Munuzuri A P 2011 Phys. Rev. E. 84 046210
Google Scholar
[28] 白婧, 关富荣, 唐国宁 2021 物理学报 70 170502
Google Scholar
Bai J, Guan F R, Tang G N 2021 Acta Phys. Sin. 70 170502
Google Scholar
[29] 李倩昀, 白婧, 唐国宁 2021 物理学报 70 098202
Google Scholar
Li Q Y, Bai J, Tang G N 2021 Acta Phys. Sin. 70 098202
Google Scholar
[30] 张秀芳, 马军, 徐莹, 任国栋 2021 物理学报 70 090502
Google Scholar
Zhang X F, Ma J, Xu Y, Ren G D 2021 Acta Phys. Sin. 70 090502
Google Scholar
[31] Wang Q, Ning W J, Dai D, Zhang Y H 2019 Plasma Process. Polym. 17 1900182
Google Scholar
[32] Sinclair J, Walhout M 2012 Phys. Rev. Lett. 108 035005
Google Scholar
[33] Fan W L, Hou X H, Tian M, Gao K Y, He Y F, Yang Y X, Liu Q, Yao J F, Liu F C, Yuan C X 2022 Plasma Sci. Technol. 24 015402
Google Scholar
[34] Fan W L, Sheng Z M, Dang W, Liang Y Q, Gao K Y, Dong L F 2019 Phys. Rev. Appl. 11 064057
Google Scholar
[35] 刘雅慧, 董梦菲, 刘富成, 田淼, 王硕, 范伟丽 2021 物理学报 70 158201
Google Scholar
Liu Y H, Dong M F, Liu F C, Tian M, Wang S, Fan W L 2021 Acta Phys. Sin. 70 158201
Google Scholar
[36] Fan W L, Liu C Y, Gao K Y, Liang Y Q, Liu F C 2021 Phys. Lett. A 396 127223
Google Scholar
[37] 白占国, 刘富成, 董丽芳 2015 物理学报 64 210505
Google Scholar
Bai Z G, Liu F C, Dong L F 2015 Acta Phys. Sin. 64 210505
Google Scholar
[38] Yang L F, Dolnik M, Zhabotinsky A M, Epstein I R 2002 Phys. Rev. Lett. 88 208303
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4224
- PDF Downloads: 70
- Cited By: 0
