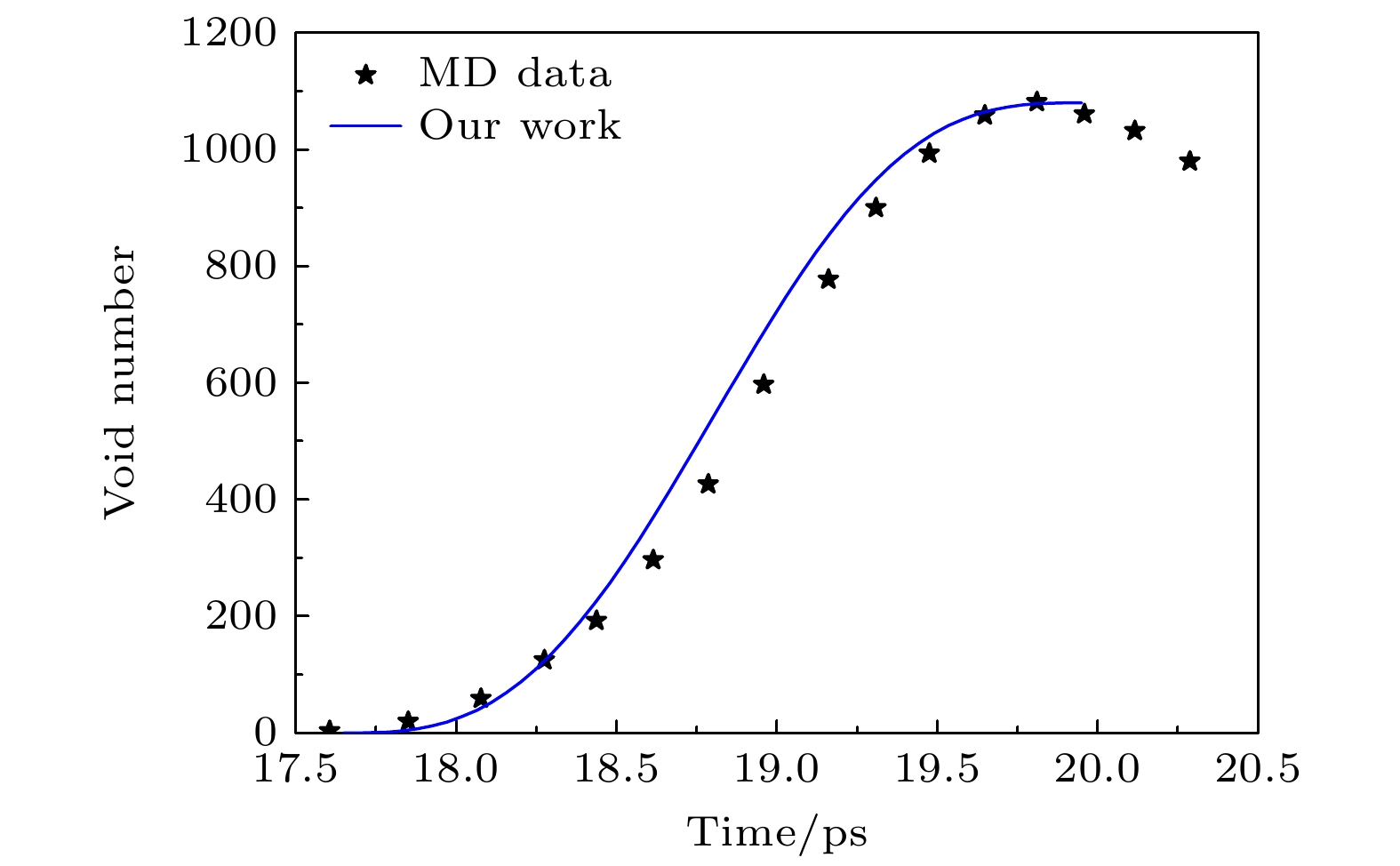
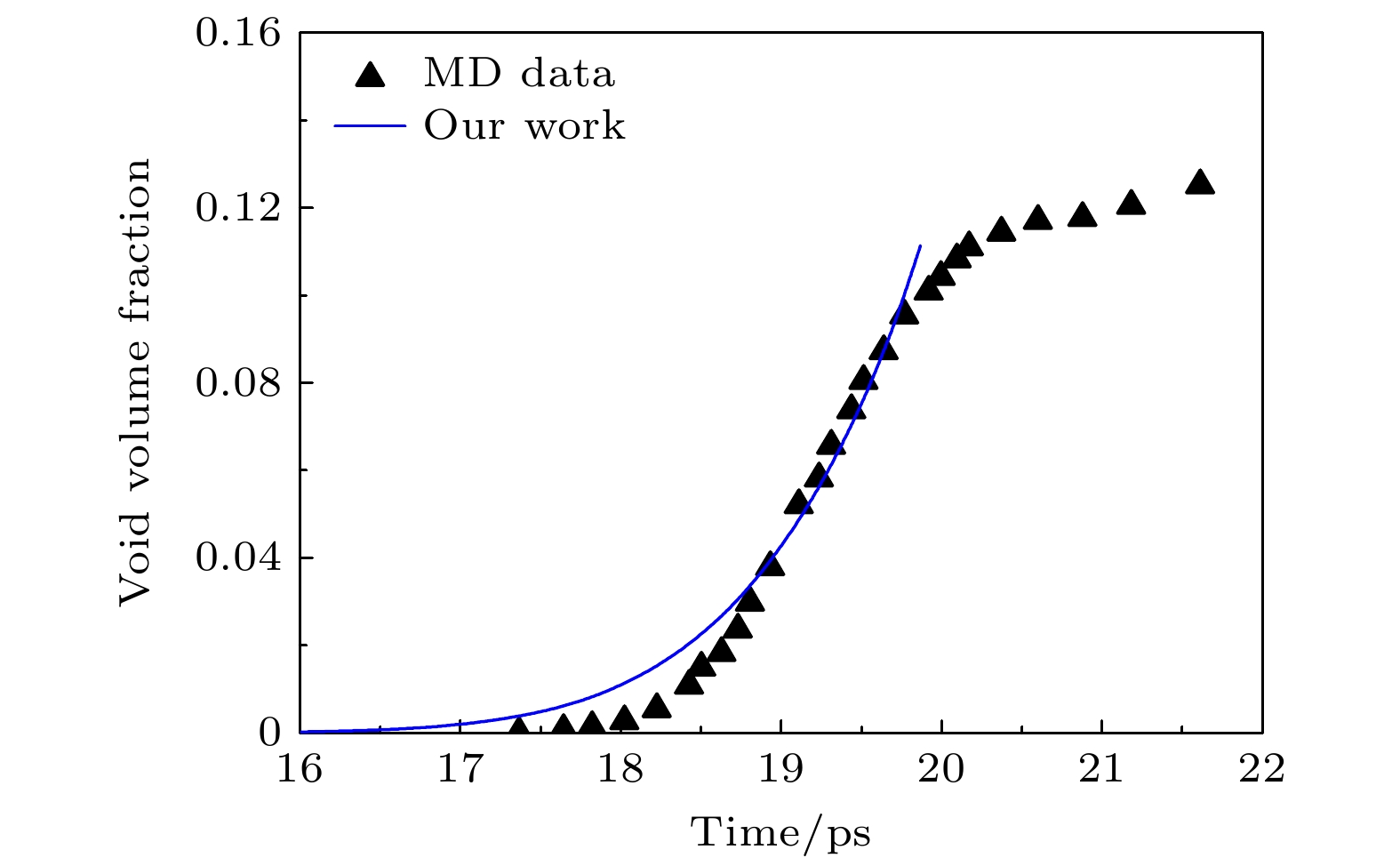
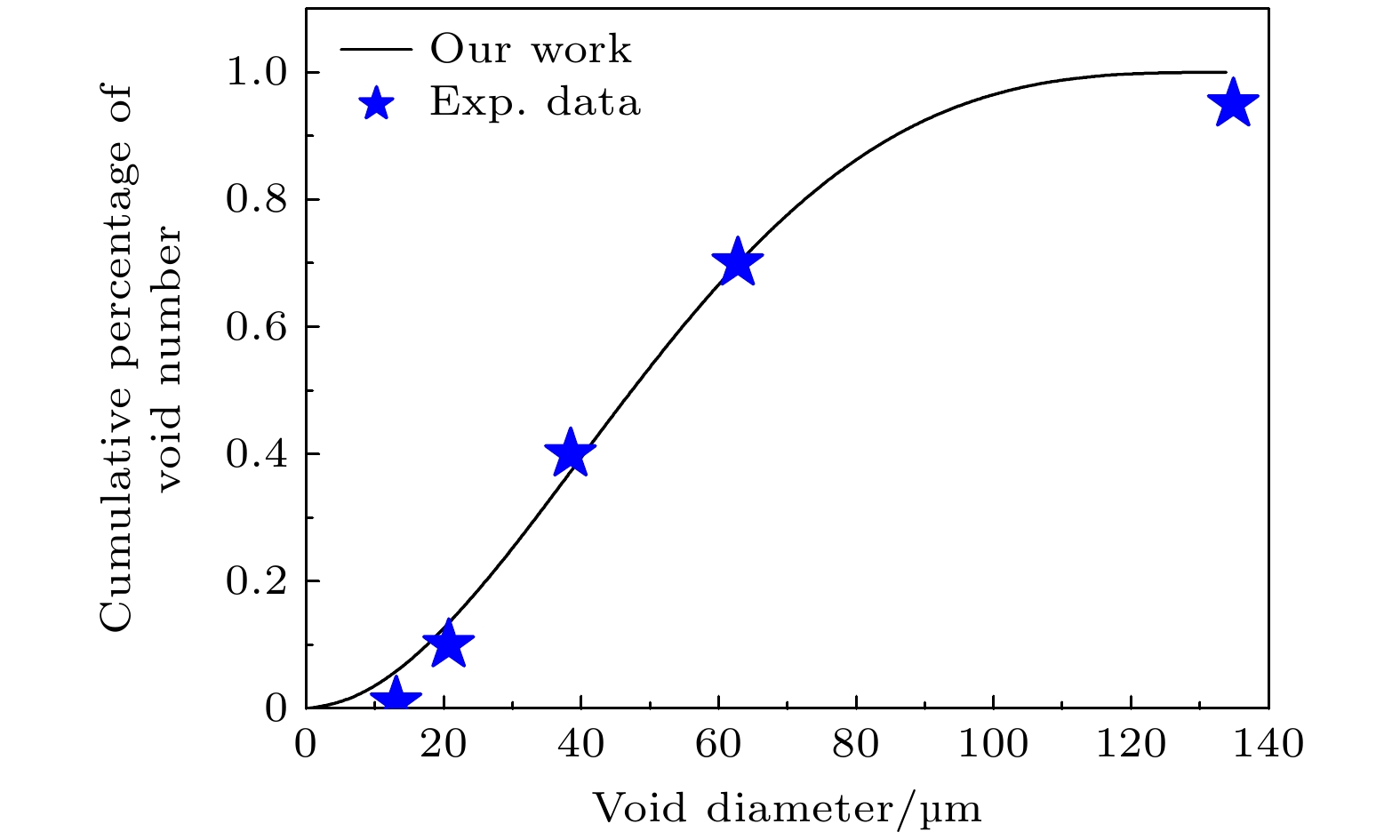
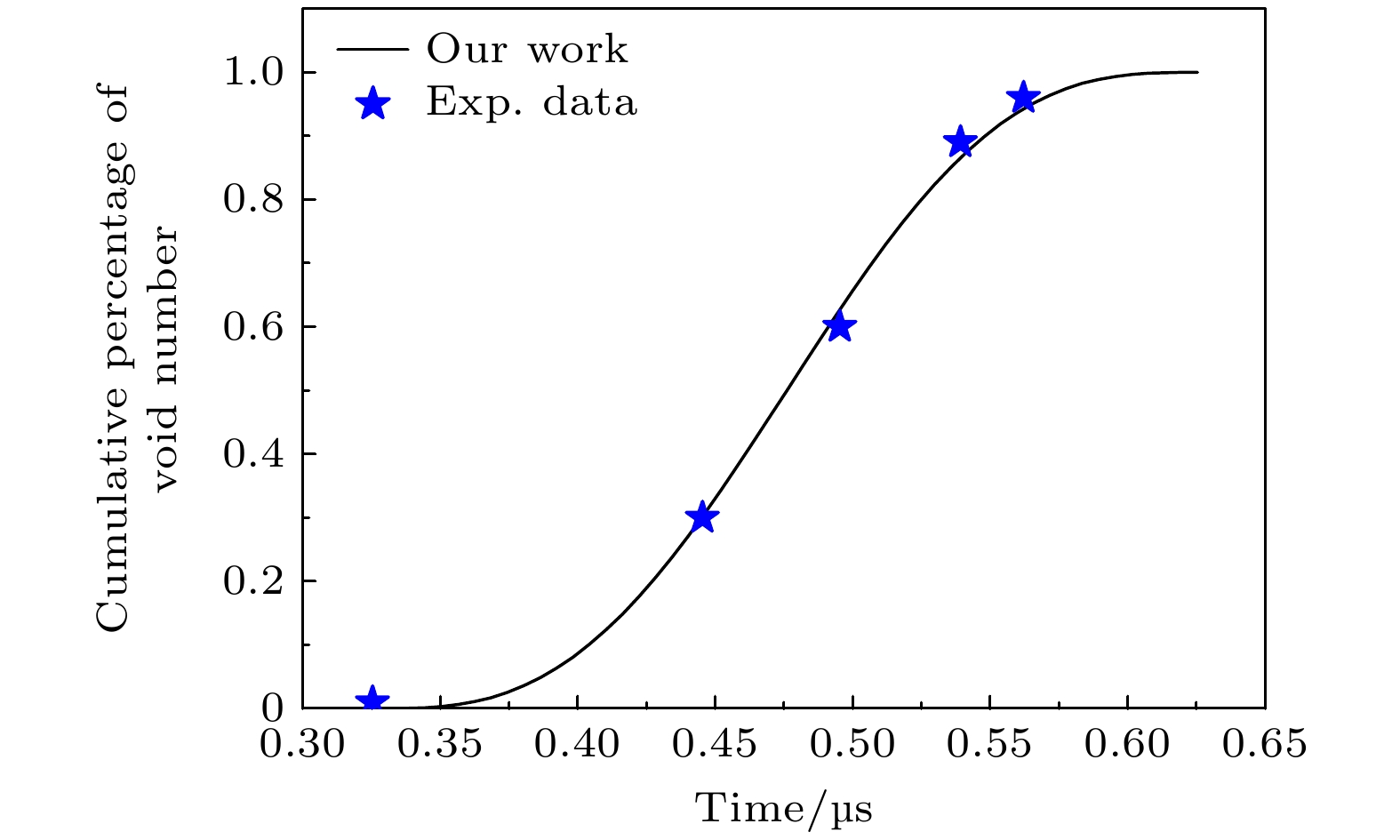
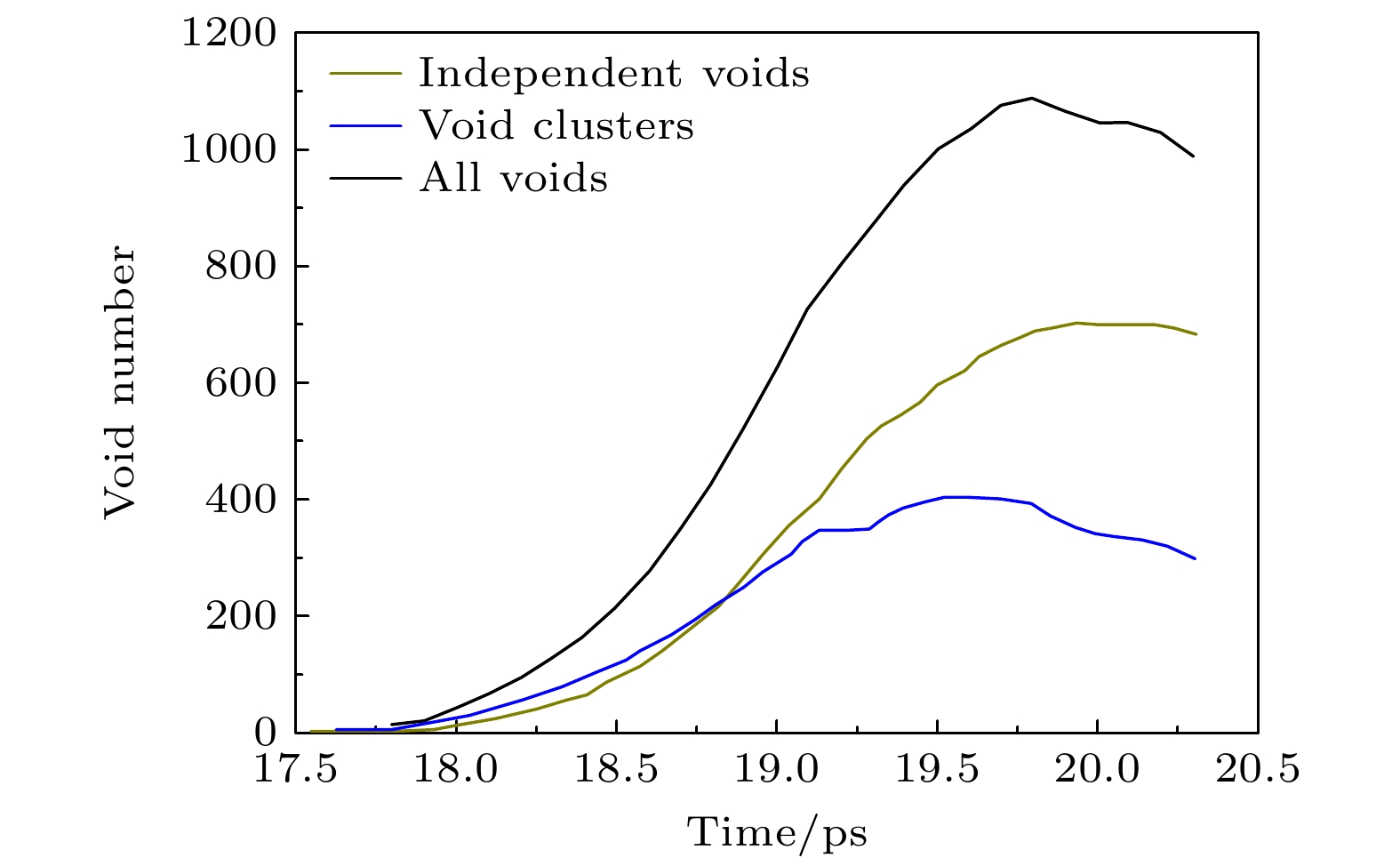
-
The development trend of spallation damage mechanics is to construct a physical model that couples information with micro-mesoscale structure of materials, which also promotes the development of numerical calculation methods, experimental techniques and theoretical research. The mechanism responsible for plastic deformation and failure of structural metal materials at high strain rates is complex and ainfluenced by heterogeneities in the micro-mesoscale structure that comprises the distribution of grain boundaries, interfaces, and pre-existing densities voids. The distribution of these mesoscale heterogeneities can provide either strengthening behavior or void nucleation sites and influence spall failure behavior. Due to the lack of evolutionary information of micro-mesoscopic void distribution characteristics, the current spallation damage model is not only restricted in its application in extreme environments with high strain rates, high pressures, and shock, but also does not effectively provide some information about the correlation between material damage and final material fragmentation particle size, which is of very concern in engineering. Therefore, it is urgent to develop a spallation damage model that can reflect the variation law of micro-mesoscopic void distribution characteristics in damaged materials. The probability distribution function of void nucleation based on cosine function is given in this work by analyzing various influencing factors in the process of void nucleation, combining the characteristics of early void growth, and considering the convenience of analytical solution. The analytical calculation results of the new probability function of void nucleation are consistent not only with the results of the variation of void number with time calculated by molecular dynamics, but also with the experimental results of tantalum spallation in the early stage of damage development, that is to say, the new probability function of void nucleation can reflect the variation law of micro-void distribution characteristics in the early stage of spallation damage to a certain extent.
-
图 2 孤立孔洞数随时间的变化
Figure 2. Number of independent voids as a function of time from MD data and our work.
图 3 所有的孔洞数随时间的变化
Figure 3. Number of sum of independent voids and void cluster as a function of time from MD data and our work.
图 4 孔洞体积份额(损伤度)随时间的变化
Figure 4. Void volume fraction as a function of time from MD data and our work.
图 5 孔洞数累积百分比随孔洞大小的变化规律
Figure 5. Cumulative percentage of void number as a void size
图 6 孔洞数累积百分比随时间的变化规律
Figure 6. Cumulative percentage of void number as a function of time.
-
[1] Seaman L, Curran D R, Shockey D A 1976 J. App. Phys. 47 4814
Google Scholar
[2] Gurson A L 1977 J. Eng. Mater. Technol. 99 2
Google Scholar
[3] Johnson J N 1981 J. App. Phys. 52 2812
Google Scholar
[4] Tonks D L, Thisell W R, Schwartz D S 2003 Shock Compression of Condensed Matter (New York: Melville) p507
[5] Molinari A, Wright T W 2005 J. Mech. Phys. Solids 53 1476
Google Scholar
[6] Chen X, Asay J R, Dwivedi S K, Field D P 2006 J. App. Phys. 99 023528
Google Scholar
[7] Dongare A M 2020 J. Mater. Sci. 55 3157
Google Scholar
[8] Trumel H, Hild F, Roy G, Pellegrini Y P, Denoual C 2009 J. Mech. Phys. Solids 57 1980
Google Scholar
[9] Pei X Y, Peng H, He H L, Li P 2015 Acta Phys. Sin. 64 054601 [裴晓阳, 彭辉, 贺红亮, 李平 2015 物理学报 64 054601]
Google Scholar
Pei X Y, Peng H, He H L, Li P 2015 Acta Phys. Sin. 64 054601
Google Scholar
[10] Rawat S, Warrier M, Chaturvedi S, Chavan V M 2011 Modelling Simul. Mater. Sci. Eng. 19 025007
Google Scholar
[11] Czarnota C, Mercier S, Molinari A 2006 Int. J. Fract. 141 177
Google Scholar
[12] Czarnota C, Jacques N, Mercier S, Molinari A 2008 J. Mech. Phys. Solids 56 1624
Google Scholar
[13] Zhai S D, Li Y H, Peng J Y, Zhang Z G, Ye X P 2016 Explo. Shock Waves 36 767 [翟少栋, 李英华, 彭建祥, 张祖根, 叶想平 2016 爆炸与冲击 36 767]
Zhai S D, Li Y H, Peng J Y, Zhang Z G, Ye X P 2016 Explo. Shock Waves 36 767
[14] Coakley J, Higginbotham A, McGonegle D, Ilavsky J, Swinburne T D, Wark J S, Rahman K M, Vorontsov V A, Dye D, Lane T J, Boutet S, Koglin J, Robinson J, Milathianaki D 2020 Sci. Adv. 6 eabb4434
Google Scholar
[15] MacNider B, Jones D, Callanan J, Beason M, Gray G T, Dattelbaum D M, Boechler N, Fensin S 2023 Sci. Adv. 9 eadi2606
Google Scholar
[16] Zhang F G, Liu J, He A M, Zhao F Q, Wang P 2022 Acta Phys. Sin. 71 244601 [张凤国, 刘军, 何安民, 赵福祺, 王裴 2022 物理学报 71 244601]
Google Scholar
Zhang F G, Liu J, He A M, Zhao F Q, Wang P 2022 Acta Phys. Sin. 71 244601
Google Scholar
[17] Zhang F G, Zhao F Q, Liu J, He A M, Wang P 2022 Acta Phys Sin. 71 034601 [张凤国, 赵福祺, 刘军, 何安民, 王裴 2022 物理学报 71 034601]
Google Scholar
Zhang F G, Zhao F Q, Liu J, He A M, Wang P 2022 Acta Phys Sin. 71 034601
Google Scholar
[18] Rawat S, Chaturvedi S 2021 Philos. Mag. 101 1119
Google Scholar
[19] Rivas J M, Zurek A K, Thissell W R, Tonks D L, Hixson R S 2000 Metall. Mater. Trans. A 31A 845
DownLoad:
Metrics
- Abstract views: 75
- PDF Downloads: 1
- Cited By: 0
