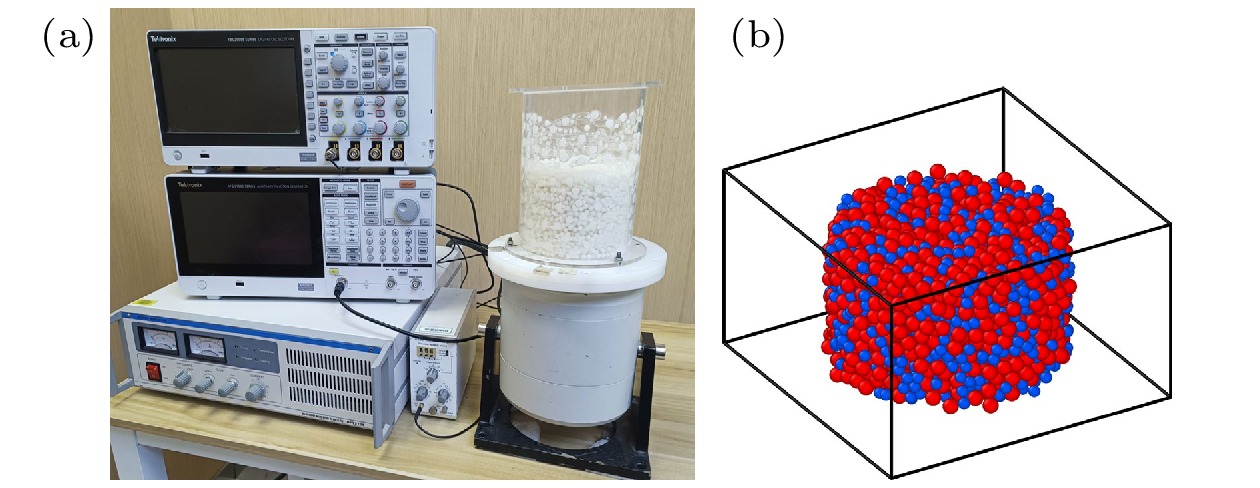
-
The packing behavior and mechanical properties of granular materials play a critical role in various engineering applications, including materials handling, construction, and energy storage. Although significant progress has been made in understanding the packing of monodisperse spheres, real-world granular systems often exhibit polydispersity, where particles of different sizes coexist. Binary systems, where the particle size ratio is adjustable, serve as a simplified model to study the structural and dynamical properties of granular materials. However, most theoretical studies on binary systems focus on idealized frictionless models, neglecting the coupled effects of friction and preparation history, and experimental data for three-dimensional systems remain limited. This study seeks to address these gaps by investigating the packing behavior of binary hard spheres under tapping through using advanced experimental techniques such as X-ray computed tomography (CT) and tap-driven compaction. The effects of particle size ratio and tap intensity on the packing fraction and local structure of binary granular systems are investigated systematically. The experimental results show that the steady-state packing fraction decreases as tap intensity increases, exhibiting similar behavior at different composition ratios. Additionally, the compaction dynamics are quantified using the Kohlrausch-Williams-Watts (KWW) relaxation function, revealing that the relaxation time decays exponentially with tap intensity increasing, independent of the composition ratio. Voronoi cell analysis demonstrates that the local volume distribution of each component in a bidisperse system composed of big particles and small particles is highly similar to that in a monodisperse system. Notably, as tap intensity decreases, the system density increases, and volume fluctuation decreases, reflecting the trends observed in monodisperse packings. Furthermore, the study highlights the influence of friction on the packing structure. For binary systems, big particles, with rougher surfaces, pack more loosely than smaller particles, and the coordination number increases with the proportion of smaller particles increasing. This suggests that frictional interactions between particles play a significant role in determining the packing density and structural stability of granular materials. The average coordination number and the steady-state packing fraction are found to be weakly dependent on each other, with friction and tap intensity (or effective temperature) being the primary factors affecting the system's structural characteristics. These findings provide a comprehensive experimental framework for understanding the packing behavior of binary granular systems, with important implications for material design in industrial applications. This study contributes to developing a more complete statistical mechanical theory for granular materials through combining both frictional effects and the influence of preparation history. Future research may extend these findings to more complex particle size distributions and explore the relationship between structural property and mechanical property.
-
Keywords:
- granular packing /
- binary systems /
- X-ray computed tomography
-
图 1 休止角$\theta $随时间$t$的变化图, 其中蓝色与红色线条分别对应8 mm和6 mm颗粒
Figure 1. Variation of the angle of repose $\theta $ with time $t$, where the blue and red lines correspond to the 8 mm and 6 mm particles, respectively.
图 2 (a)实验装置; (b)重建的双分散体系的堆积结构(红色与蓝色粒子分别对应8 mm和6 mm颗粒)
Figure 2. (a) Experimental setup; (b) reconstructed packing structure of the binary system (Red and blue spheres represent the 8 mm and 6 mm particles, respectively).
图 3 Voronoi元胞示意图
Figure 3. Schematic diagram of Voronoi cells.
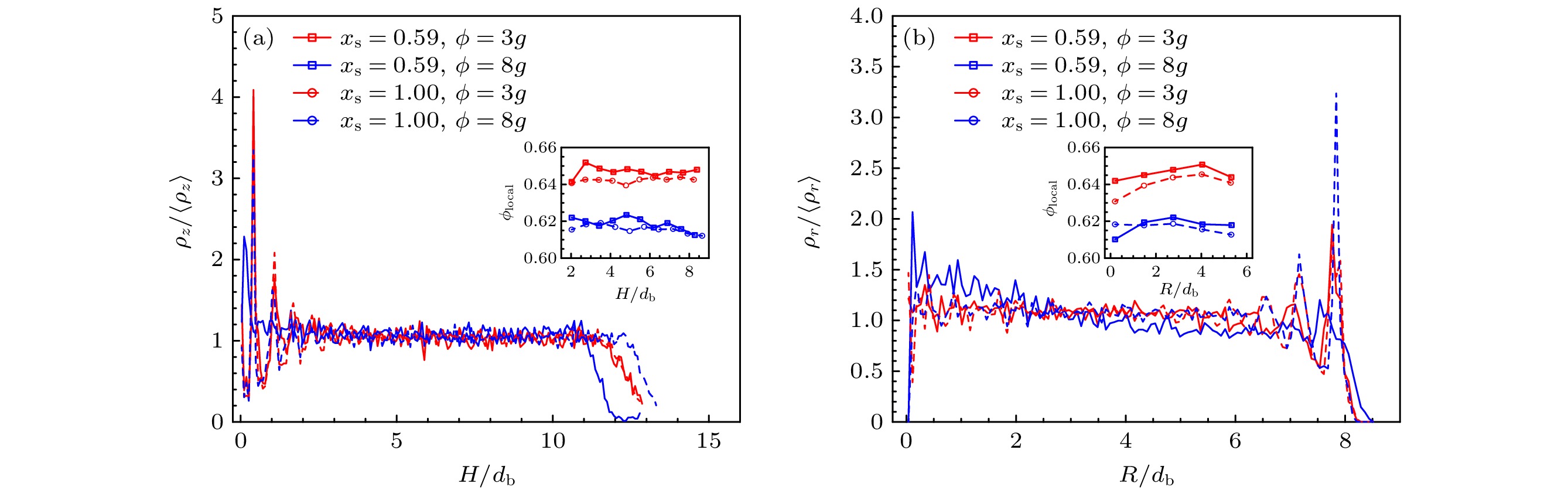
图 4 (a)归一化后的颗粒数密度在垂直方向的分布图, 插图为局部体积分数在垂直方向的分布图; (b)归一化后的颗粒数密度在径向的分布图, 插图为局部体积分数在径向的分布图
Figure 4. (a) Distribution of normalized particle number density in the vertical direction, the inset shows the distribution of local volume fraction in the vertical direction; (b) distribution of normalized particle number density in the radial direction, the inset shows the distribution of local volume fraction in the radial direction.
图 5 不同${x_{\text{s}}}$的双(单)分散体系, 在不同振动强度$\varGamma $下的弛豫过程, 图中横轴为振动次数
Figure 5. Relaxation processes of binary (monodisperse) systems with different ${x_{\text{s}}}$ under various tap intensities $\varGamma $, where the horizontal axis represents the number of taps.
图 6 不同${x_{\text{s}}}$的双分散体系弛豫时间$\tau $随振动强度$\varGamma $的函数关系
Figure 6. Relaxation time $\tau $ as a function of tap intensity $\varGamma $ for binary systems with different concentration ${x_{\text{s}}}$.
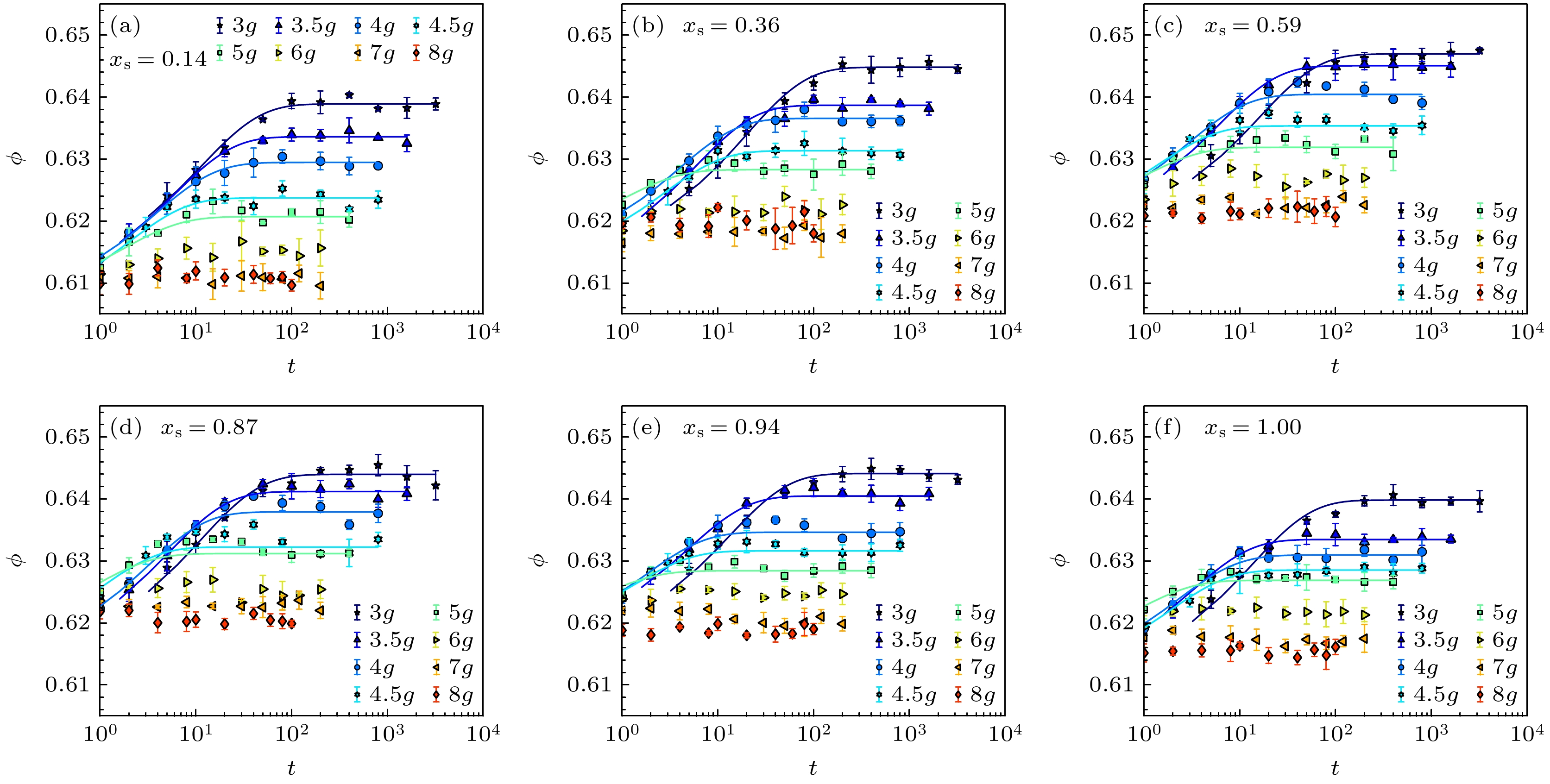
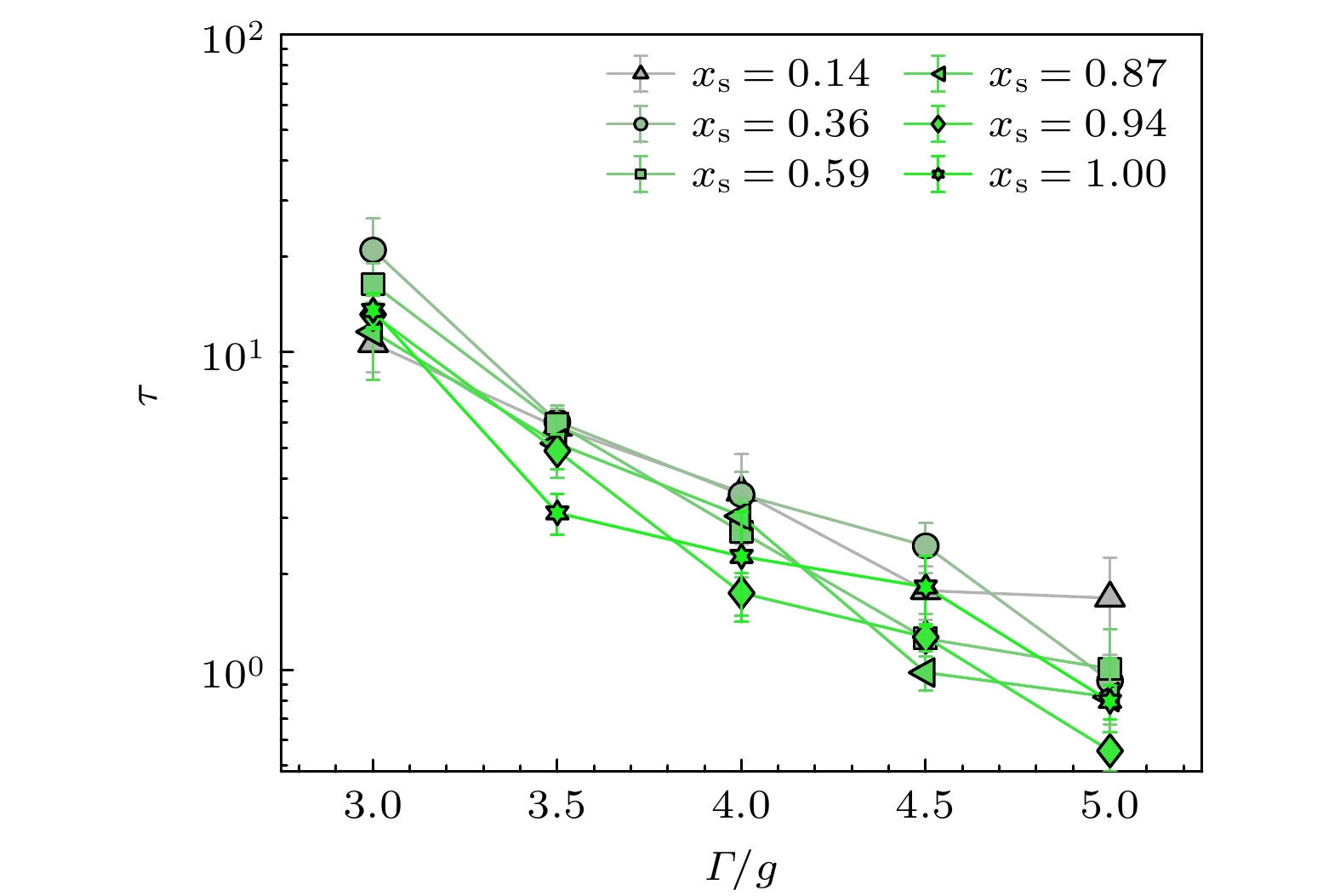
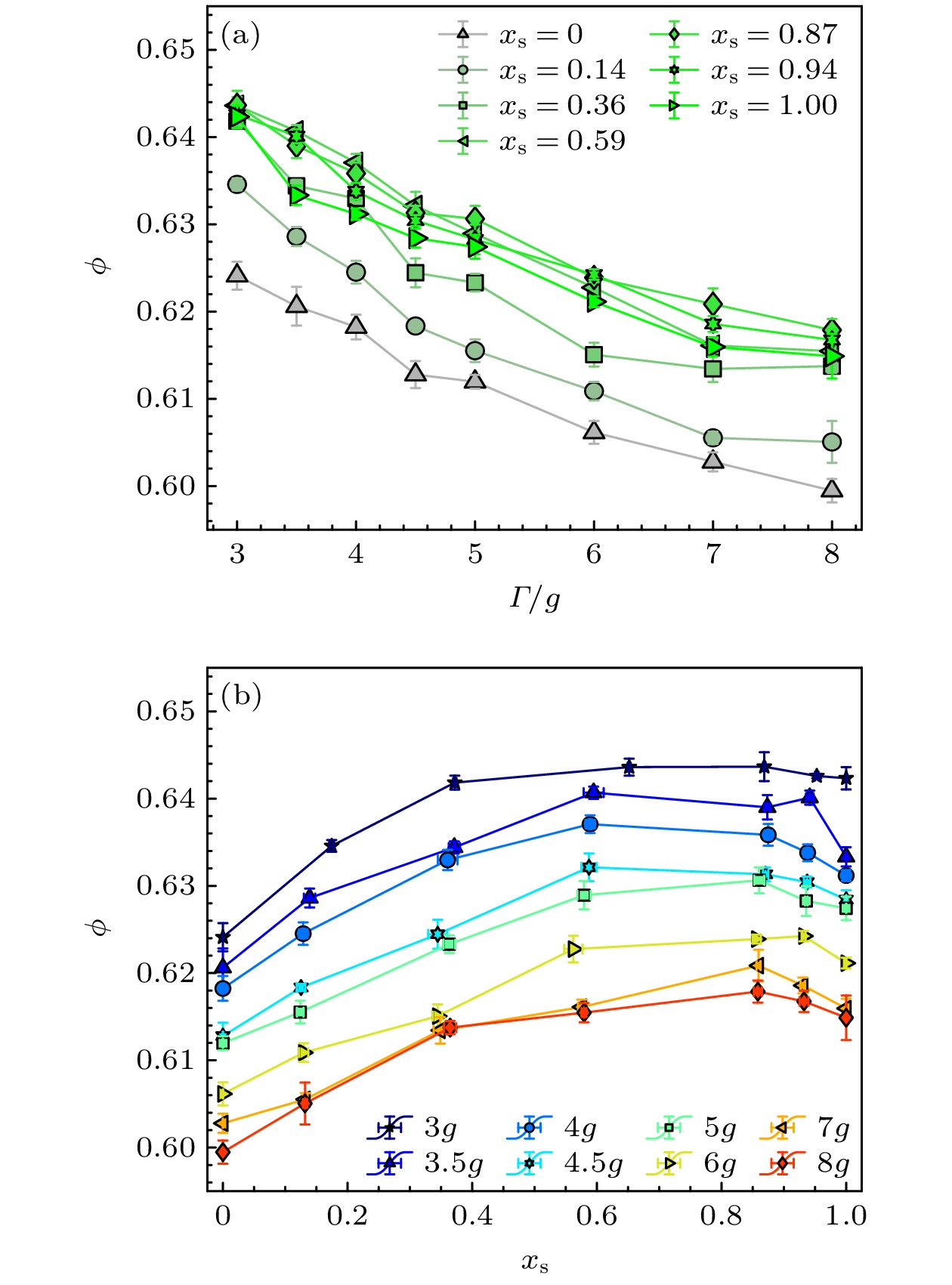
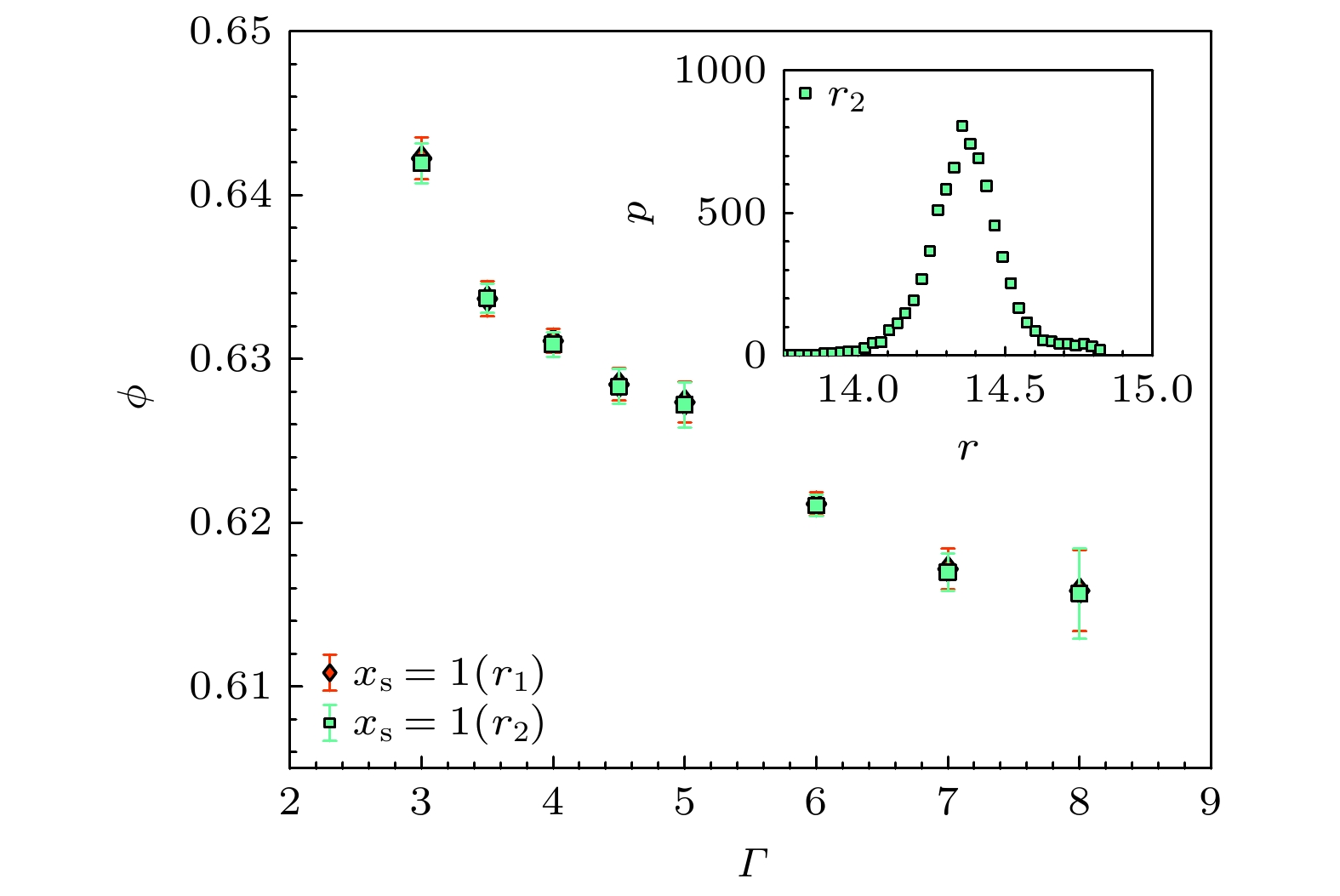
图 7 (a)不同成分比${x_{\text{s}}}$下, 体系稳态体积分数$\phi $关于振动强度$\varGamma $的函数关系; (b) 不同$\varGamma $下, $\phi $关于${x_{\text{s}}}$的函数关系; 去除边界颗粒后, 双分散体系的成分比${x_{\text{s}}}$会产生轻微偏移, 致使(b)中数据呈现偏差; 本文中所有图例${x_{\text{s}}}$值表示相同初始混合比下, 经边界颗粒去除后不同振动强度体系的均值
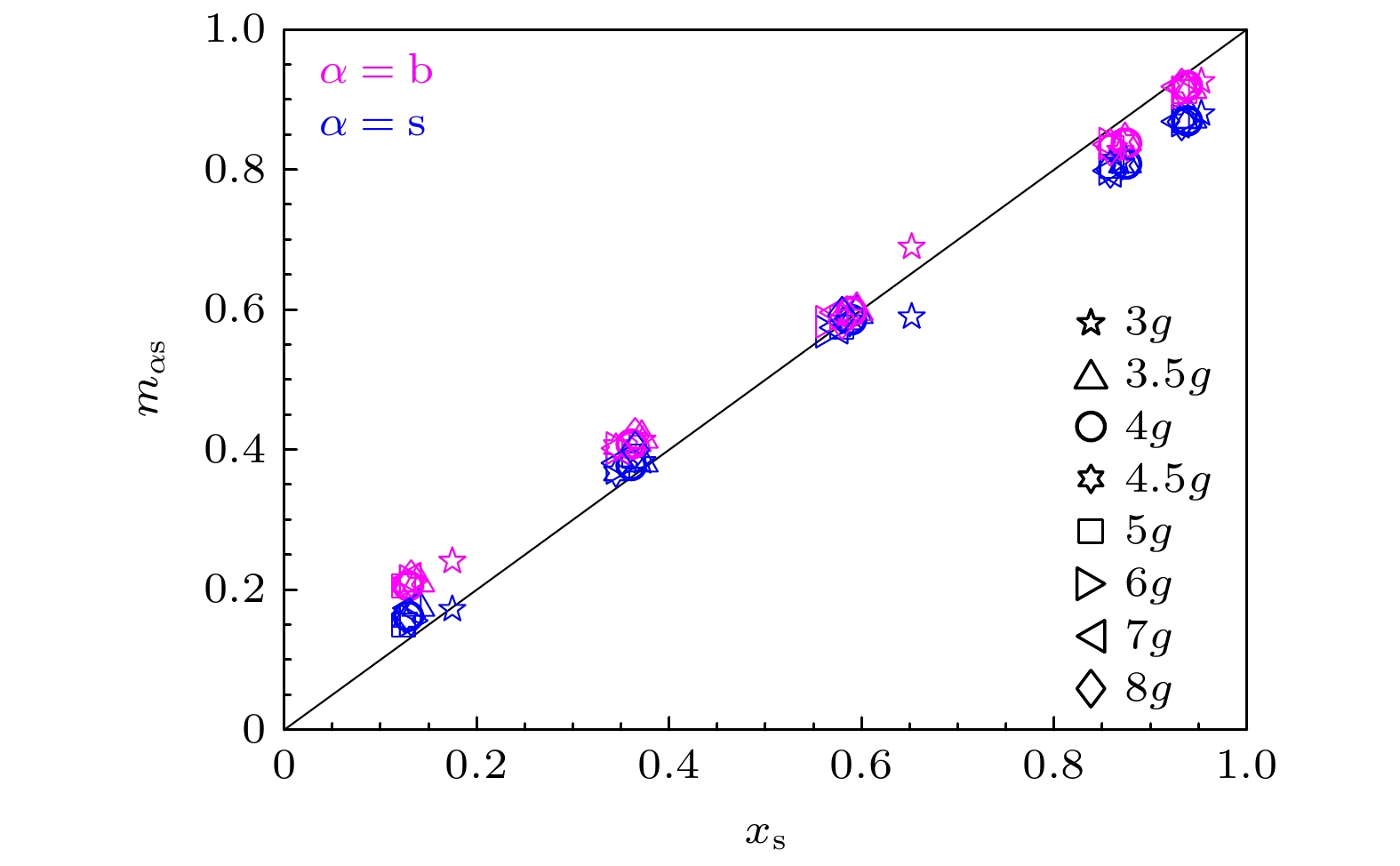
Figure 7. (a) The packing fraction of steady states $\phi $ as a function of tap intensity $\varGamma $ for different concentration ${x_{\text{s}}}$; (b) $\phi $ as a function of ${x_{\text{s}}}$ for different $\varGamma $. After removing boundary particles, the composition ratio of the binary system exhibits slight deviations from the initial mixture proportion, leading to discrepancies in the data shown in panel (b). All legend values in this study represent averaged values across systems with identical initial mixing ratios under varying vibration intensities after boundary particle removal.
图 8 两种情况下体积分数与振动强度的关系图, 插图为${r_2}$的半径的概率分布图
Figure 8. Relationship between volume fraction and vibration intensity in two cases, the inset shows the probability distribution of the radius.
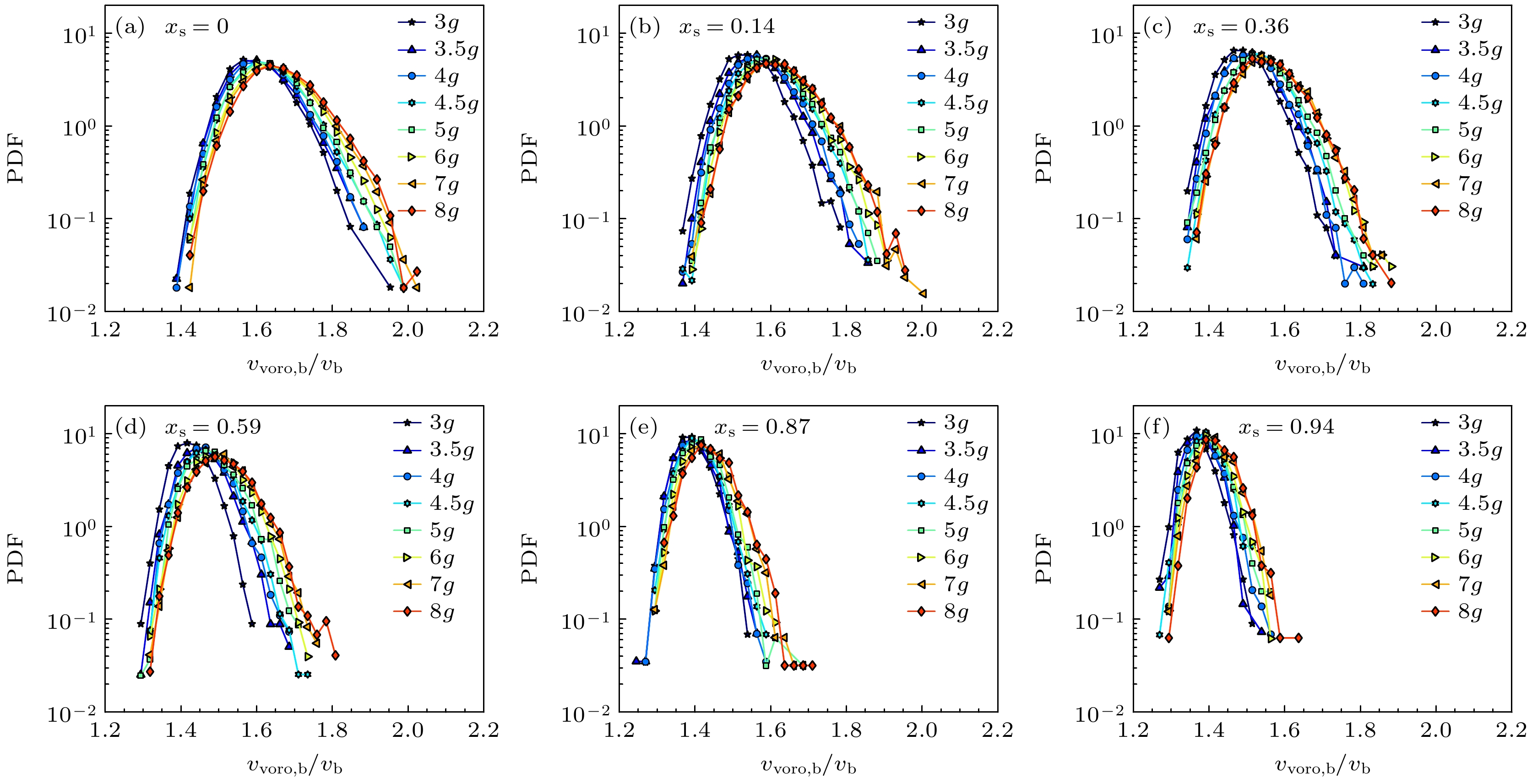
图 9 不同成分比${x_{\text{s}}}$下, 稳态堆积的大球径向Voronoi体积${v_{{\text{voro, b}}}}$的概率分布随振动强度$\varGamma $的演化
Figure 9. Evolution of probability distribution for radical Voronoi volumes ${v_{{\text{voro, b}}}}$ for big particles in steady-state packings with different concentration ${x_{\text{s}}}$ as a function of vibration tap intensity $\varGamma $.
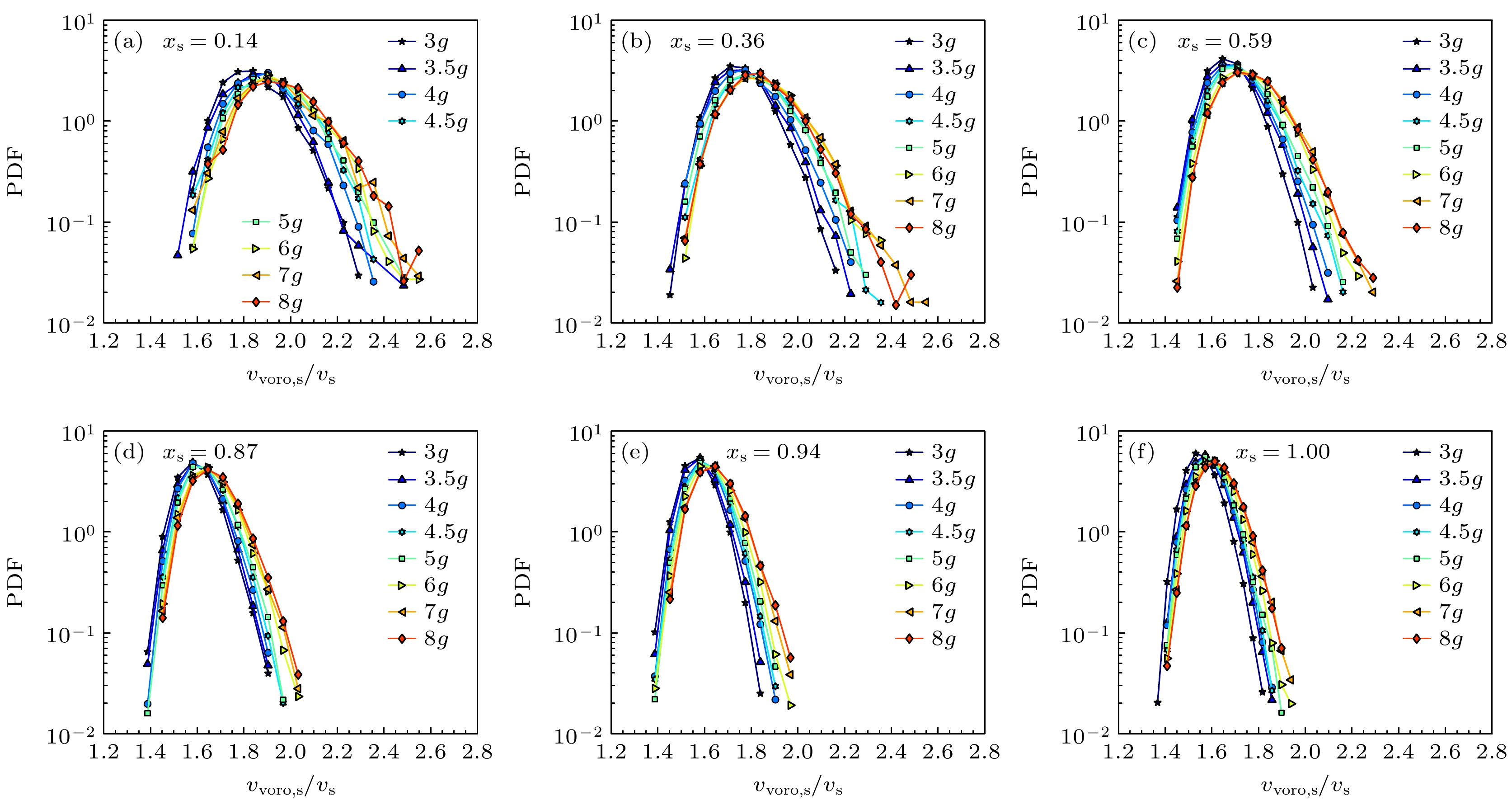
图 10 不同成分比${x_{\text{s}}}$下, 稳态堆积的小球径向Voronoi体积${v_{{\text{voro, s}}}}$的概率分布随振动强度$\varGamma $的演化
Figure 10. Evolution of probability distribution for radical Voronoi volumes ${v_{{\text{voro, s}}}}$ for big particles in steady-state packings with different concentration ${x_{\text{s}}}$ as a function of vibration tap intensity $\varGamma $.
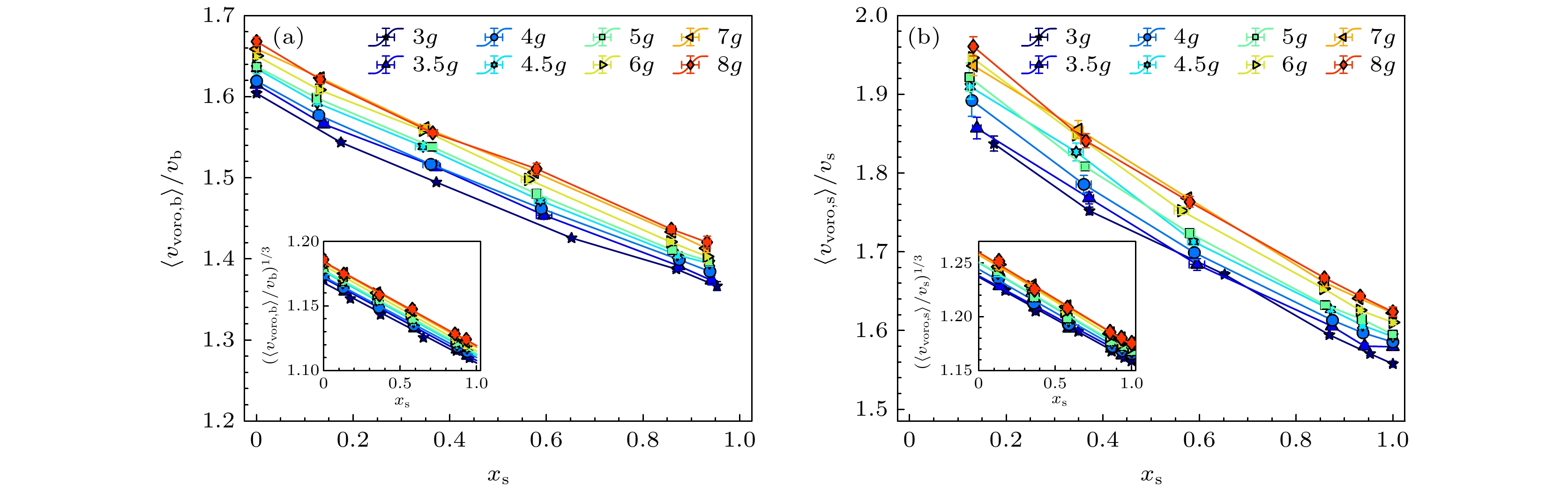
图 11 不同振动强度$\varGamma $下 (a)大球和(b)小球的平均Voronoi体积$\left\langle {{v_{{\text{voro}}}}} \right\rangle $随不同成分比${x_{\text{s}}}$的演化. 插图为${\left\langle {{v_{{\text{voro}}}}} \right\rangle ^{1/3}}$和${x_{\text{s}}}$的关系
Figure 11. Evolution of the average Voronoi volume of (a) big particles and (b) small particles with varying concentration ${x_{\text{s}}}$ under different tap intensities $\varGamma $. The inset is relation between ${\left\langle {{v_{{\text{voro}}}}} \right\rangle ^{1/3}}$ and ${x_{\text{s}}}$.
图 12 不同$\varGamma $下, 相分离程度$\alpha $关于${x_{\text{s}}}$的函数关系
Figure 12. Functional relationship between phase separation degree $\alpha $ and ${x_{\text{s}}}$ at different values of $\varGamma $.
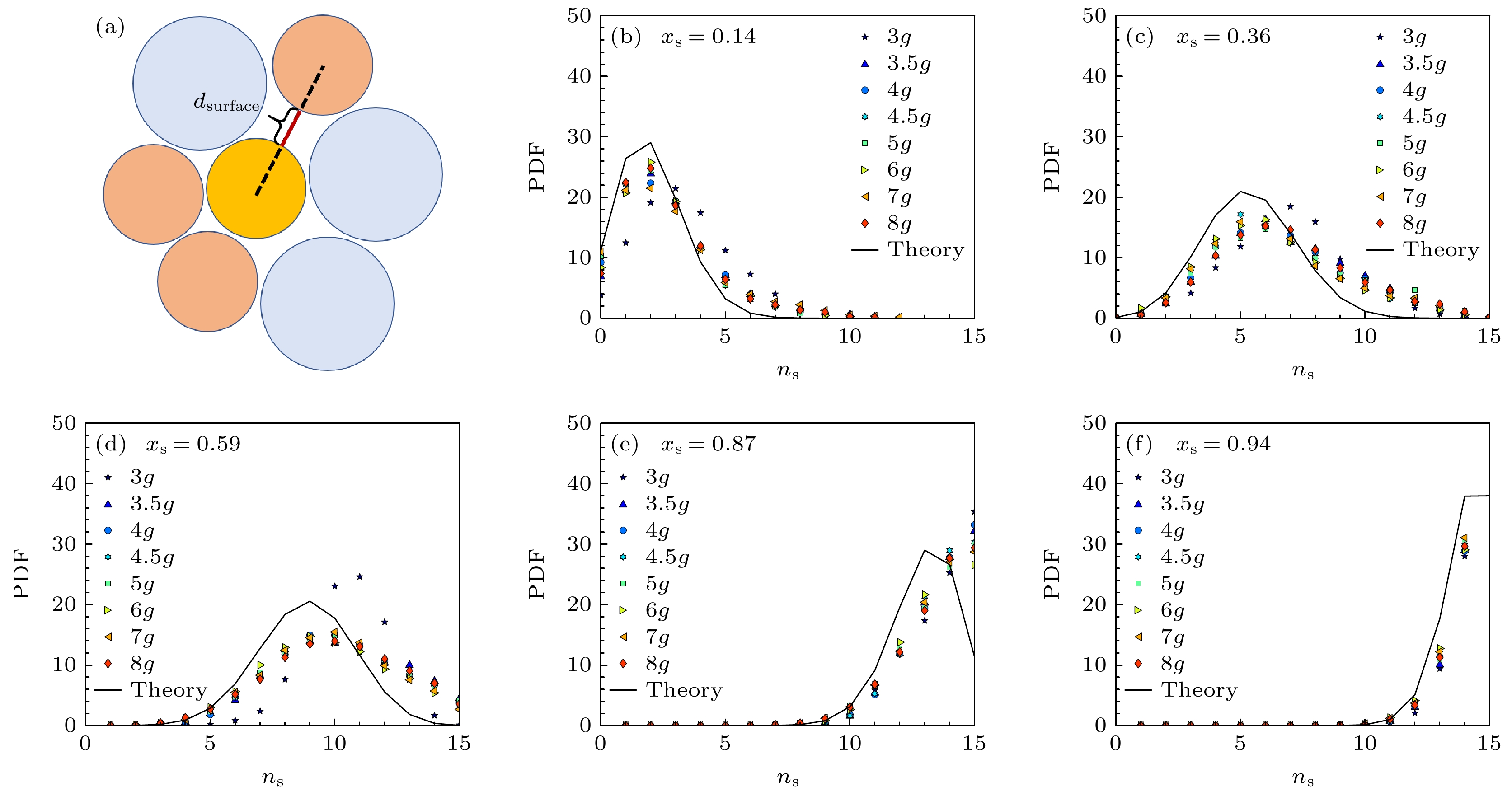
图 13 (a)二维的表面间距示意图; (b)—(f)不同成分比${x_{\text{s}}}$下, 15个邻近粒子的小球数${n_{\text{s}}}$的概率分布
Figure 13. (a) Schematic illustration of surface-to-surface distance in two dimensions; (b)–(f) probability distribution of the number of small particles among 15 nearest neighbors for different concentration ${x_{\text{s}}}$.
图 14 Voronoi近邻中平均小球占比${m_{{\text{α s}}}}$关于成分比${x_{\text{s}}}$的函数, 其中$\alpha $为中心粒子的类型
Figure 14. Average fraction of small particles in Voronoi neighbors ${m_{{\text{α s}}}}$ as a function of concentration ${x_{\text{s}}}$, $\alpha $ is the type of the central particle .
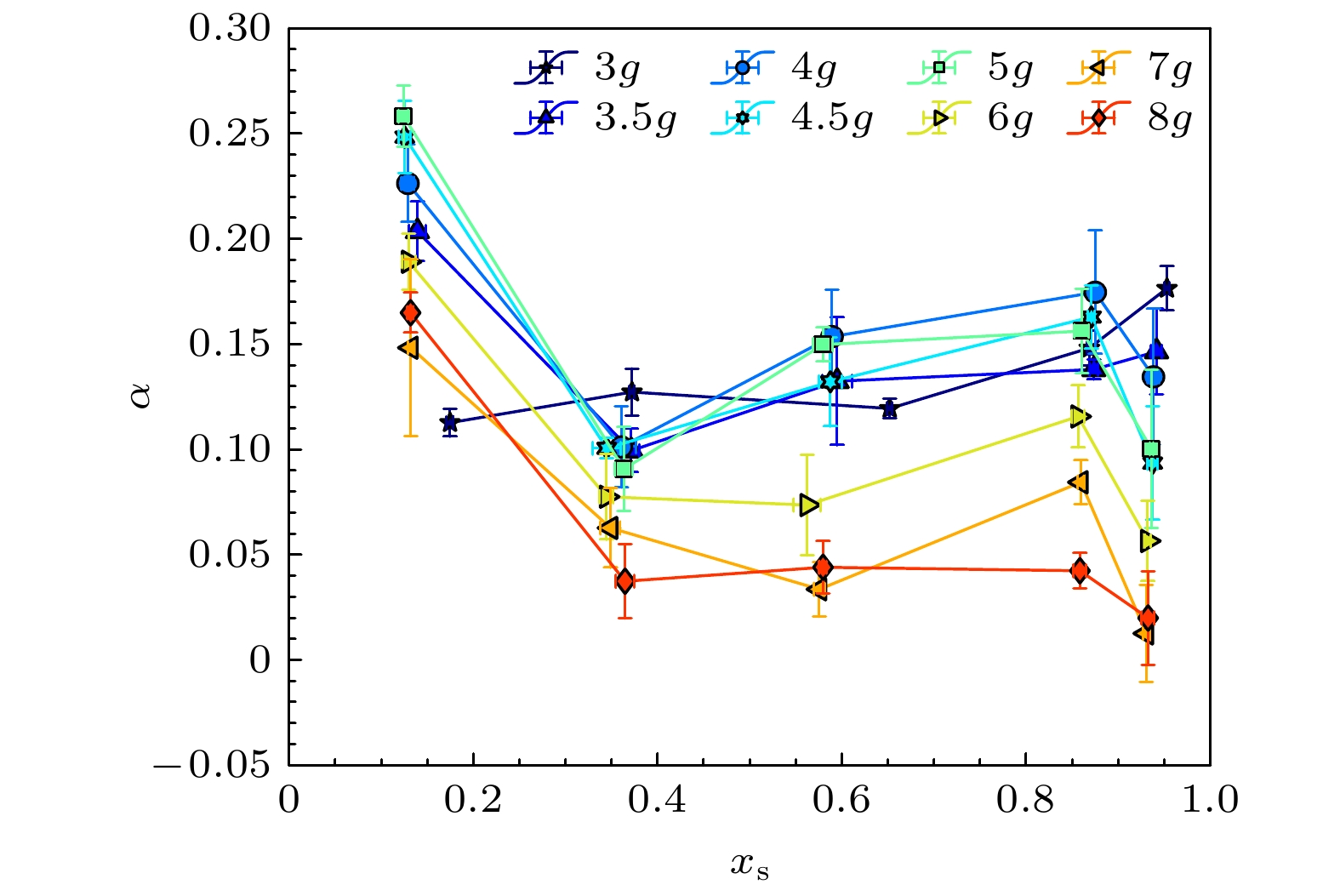
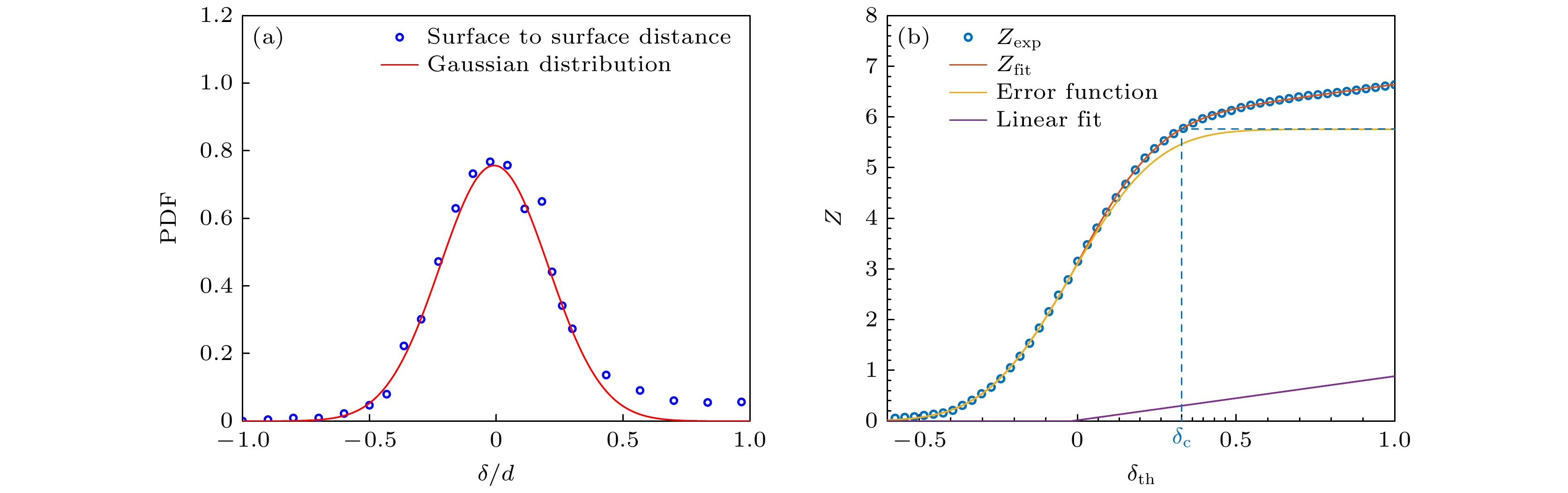
图 15 (a)近邻颗粒的表面间距的概率密度分布和高斯拟合; (b) 平均接触数$Z$和接触阈值${\delta _{{\text{th}}}}$的函数关系
Figure 15. (a) Probability density distribution of surface-to-surface distances between neighboring particles and its Gaussian fit; (b) the relation between the average coordination number $Z$ and the contact threshold ${\delta _{{\text{th}}}}$.
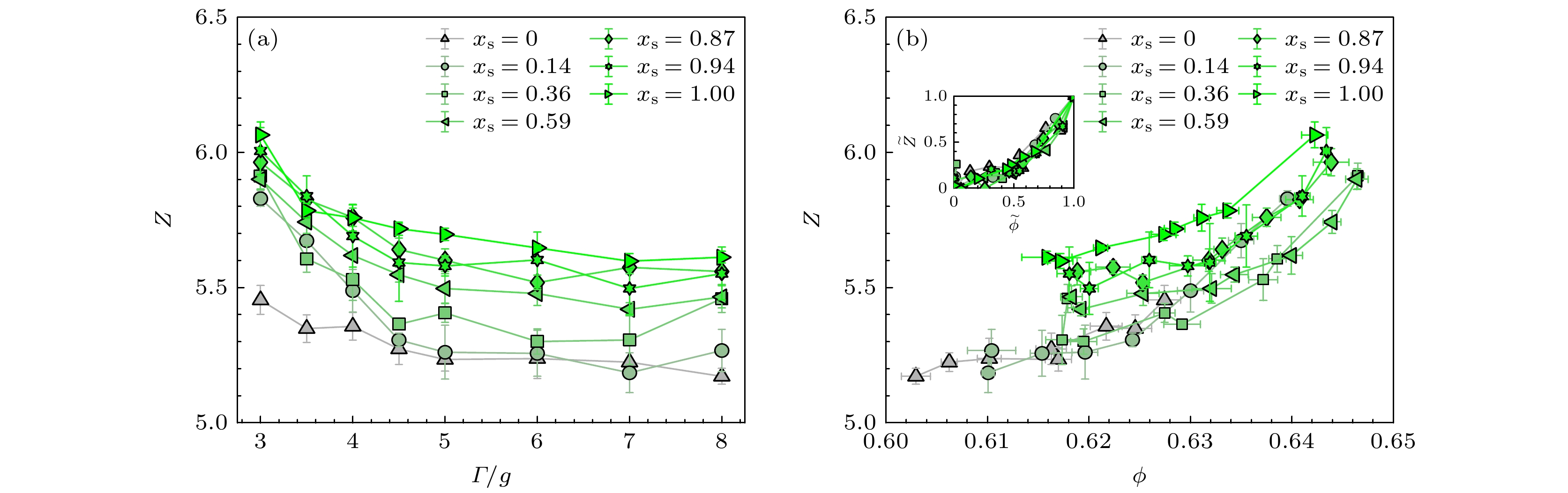
图 16 不同成分比${x_{\text{s}}}$下, (a)接触数Z关于振动强度Γ的函数关系; (b)体系稳态体积分数$\phi $关于接触数Z的函数关系; 插图为归一化后体积分数$ \tilde \phi $与接触数$\tilde Z$的关系
Figure 16. (a) Relationship between the average coordination number Z and the tap intensity Γ for different concentration ${x_{\text{s}}}$; (b) relation between the steady-state volume fraction $\phi $ and the coordination number; inset is the relation between the normalized volume fraction $ \tilde \phi $ and the coordination number $\tilde Z$.
-
[1] Parisi G, Zamponi F 2010 Rev. Mod. Phys. 82 789
Google Scholar
[2] Burin A 2006 Phys. Today 59 64
[3] Haslach Jr H 2002 Appl. Mech. Rev. 55 B62
Google Scholar
[4] Torquato S, Stillinger F H 2010 Rev. Mod. Phys. 82 2633
Google Scholar
[5] Baule A, Morone F, Herrmann H J, Makse H A 2018 Rev. Mod. Phys. 90 015006
Google Scholar
[6] Yuan Y, Xing Y, Zheng J, Li Z F, Yuan H F, Mang S Y, Zeng Z K, Xia C J, Tong H, Kob W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 127 018002
Google Scholar
[7] Xing Y, Yuan Y, Yuan H F, Zhang S Y, Zeng Z K, Zheng X, Xia C J, Wang Y J 2024 Nat. Phys. 20 8
Google Scholar
[8] Kou B Q, Cao Y X, Li J D, Xia C J, Li Z F, Dong H P, Zhang A, Zhang J, Kob W, Wang Y J 2017 Nature 551 360
Google Scholar
[9] Aste T, Weaire D 2001 Phys. Bl. 57 72
[10] Cumberland D, Crawford R J 1987
[11] German R M 1989 Particle Packing Characteristics (Metal Powder Industries Federation
[12] Onoda G Y, Liniger E G 1990 Phys. Rev. Lett. 64 2727
Google Scholar
[13] Dong K J, Yang R Y, Zou R P, Yu A B 2006 Phys. Rev. Lett. 96 169903
Google Scholar
[14] Jerkins M, Schröter M, Swinney H L, Senden T J, Saadatfar M, Aste T 2008 Phys. Rev. Lett. 101 018301
Google Scholar
[15] Silbert L E 2010 Soft Matter 6 2918
Google Scholar
[16] Vinutha H A, Sastry S 2016 Nat. Phys. 12 578
Google Scholar
[17] Sohn H Y, Moreland C 1968 Can. J. Chem. Eng. 46 162
Google Scholar
[18] Santiso E, Müller E A 2002 Mol. Phys. 100 2461
Google Scholar
[19] Brouwers H J H 2006 Phys. Rev. E 74 031309
Google Scholar
[20] Desmond K W, Weeks E R 2014 Phys. Rev. E 90 022204
Google Scholar
[21] Peng A, Yuan Y, Wang Y 2023 NSO 2 20220069
Google Scholar
[22] Xia C J, Li J D, Cao Y X, Kou B Q, Xiao X H, Fezzaa K, Xiao T Q, Wang Y J 2015 Nat. Commun. 6 8409
Google Scholar
[23] Gooch J W (Gooch J W ed) 2011 Encyclopedic Dictionary of Polymers (New York, NY: Springer New York) pp413-414
[24] Biazzo I, Caltagirone F, Parisi G, Zamponi F 2009 Phys. Rev. Lett. 102 195701
Google Scholar
[25] Yuan H F, Zhang Z, Kob W, Wang Y J 2021 Phys. Rev. Lett. 127 278001
Google Scholar
[26] Hopkins A B, Stillinger F H, Torquato S 2013 Phys. Rev. E 88 022205
Google Scholar
[27] Danisch M, Jin Y L, Makse H A 2010 Phys. Rev. E 81 051303
Google Scholar
[28] Li Z F, Zeng Z K, Xing Y, Li J D, Zheng J, Mao Q H, Zhang J, Hou M Y, Wang Y J 2021 Sci. Adv. 7 eabe8737
Google Scholar
[29] Matsumura S, Richardson D C, Michel P, Schwartz S R, Ballouz R L 2014 Mon. Not. Ro. Astron. Soc. 443 3368
Google Scholar
[30] Aste T, Saadatfar M, Senden T J 2005 Phys. Rev. E 71 061302
Google Scholar
DownLoad:
Metrics
- Abstract views: 442
- PDF Downloads: 9
- Cited By: 0
