Frontiers in non-Hermitian physics
传统量子力学所描述的系统通常是独立并且与外界没有相互作用的理想系统, 这就要求哈密顿量为厄米算符以保证系统随时间演化的幺正性以及能谱的完全实数性. 然而在实际工作中, 由于非厄米哈密顿量描述的简便性, 其被技术性的引入描述一些唯象理论. 如 Herman Feshbach提出投影算符理论应用于核物理的研究. 非厄米哈密顿量也可在量子光学中描述耗散过程, 在量子化学中描述化学反应过程等. 非厄米哈密顿量在描述开放系统中衰减机制、有限的特征时间以及退相干等现象时取得了巨大的成功, 但是由于它所带来的复数本征值, 其依然被大家认为是非物理的. 二十世纪九十年代, Bender和 Boettcher发现具有宇称-时间反演 (PT)对称性的非厄米算符依然可以具有完全实数的能谱, 即可观测量为实数. 这一所谓的 “非物理公认”被推翻. 随后很多研究者致力于非厄米系统的研究, 发现了非厄米系统中独有的奇异点、PT 对称相变、几率震荡等诸多新奇物理性质和现象. 基于傍轴近似下麦克斯韦方程与薛定谔方程的类比, 研究者们在光学系统中成功地仿真了非厄米哈密顿量. 非厄米量子力学的基本理论在光学平台上得到了有效的检验. 这些基础性工作极大地促进了非厄米理论与实验的快速发展.
除了静力学上的特殊性质, 非厄米系统还表现出许多在厄米系统中从未出现过的特殊动力学行为, 其中一个显著特征是奇异点动力学. 奇异点是非厄米系统特有的能谱简并结构, 其对应的本征态出现合并, 导致不完备的希尔伯特空间. 狄拉克几率不守恒以及奇异点的存在造就了非厄米系统不同于厄米系统的特殊动力学行为. 奇异点相关的非平衡物理在单体系统中得到了深入的研究, 在多体系统中也有涉及. 非厄米性和相互作用之间的结合必定会产生奇异的量子多体效应, 并且可以极大地改变厄米物理中已经确立的宏观行为.
非厄米物理广泛存在于包括光学、声学、经典波、冷原子、凝聚态体系等物理系统中, 其中具有许多超出厄 米系统范式的新颖物理性质, 因此对非厄米新奇物性的深入理解和精准调控可以为非厄米物理在各类系统中的应用奠定基础. 近十年, 这一领域取得了许多令人瞩目的研究成果, 国内外许多优秀的科研团队做出了卓越的研究成果. 相关研究成果不仅具有重要的学术价值, 同时也从一定程度上引领了物理学的发展以及未来科技进步的方向. 基于此, 本专题特别邀请了活跃在该领域的专家学者, 从不同的物理系统, 多方面的视角去介绍该领域的研究背景、相关重要研究问题以及未来可能的发展方向, 希望本专题可以对感兴趣的读者有所裨益.
除了静力学上的特殊性质, 非厄米系统还表现出许多在厄米系统中从未出现过的特殊动力学行为, 其中一个显著特征是奇异点动力学. 奇异点是非厄米系统特有的能谱简并结构, 其对应的本征态出现合并, 导致不完备的希尔伯特空间. 狄拉克几率不守恒以及奇异点的存在造就了非厄米系统不同于厄米系统的特殊动力学行为. 奇异点相关的非平衡物理在单体系统中得到了深入的研究, 在多体系统中也有涉及. 非厄米性和相互作用之间的结合必定会产生奇异的量子多体效应, 并且可以极大地改变厄米物理中已经确立的宏观行为.
非厄米物理广泛存在于包括光学、声学、经典波、冷原子、凝聚态体系等物理系统中, 其中具有许多超出厄 米系统范式的新颖物理性质, 因此对非厄米新奇物性的深入理解和精准调控可以为非厄米物理在各类系统中的应用奠定基础. 近十年, 这一领域取得了许多令人瞩目的研究成果, 国内外许多优秀的科研团队做出了卓越的研究成果. 相关研究成果不仅具有重要的学术价值, 同时也从一定程度上引领了物理学的发展以及未来科技进步的方向. 基于此, 本专题特别邀请了活跃在该领域的专家学者, 从不同的物理系统, 多方面的视角去介绍该领域的研究背景、相关重要研究问题以及未来可能的发展方向, 希望本专题可以对感兴趣的读者有所裨益.

2022, 71 (13): 130701.
doi: 10.7498/aps.71.20220425
Abstract +
Quantum precision measurement is based on the basic principle of quantum mechanics by using the interaction between light, atoms and magnetism to measure physical quantities, also known as precision measurements based on microscopic particle systems and their quantum states. As an important means of quantum precision measurement, interferometer precision measurement technology has great application value in quantum communication. The linear interferometer measures the magnitude of the physical quantity by using the phase change obtained from the measurements, but measurement accuracy is limited and unable to meet the requirements of today's scientific problems for the precision measurement of some physical quantities. On this basis, nonlinear interferometer is able to take advantage of the quantum entangled state, that is, using the two light fields of quantum correlation characteristics to realize quantum enhanced precision measurement, thus greatly improving the measurement sensitivity, Therefore, the scope of application is wider, but the preparation of quantum entangled states has many limitations in practical manipulation. With the maturity of experimental conditions and technology, how to use both of these interferometers to further improve the measurement accuracy of the phase signal so as to break the limitation to shot noise, breaking the standard quantum limit and even approaching to the Heisenberg limit has become a frontier research topic . In this paper, we introduce several methods to improve the accuracy of parameter evaluation in the measurement process by using linear (including an atomic/photon interferometer) and nonlinear interferometer to call quantum resources at different stages. High-precision measurement can be achieved by inputting non-classical states into the interferometer, such as compressed state, bi-fock state, and NOON state. And we also introduce the weak measurement developed for the direct observation of quantum states and its application to non-Hermitian systems, and the multiparameter measurement proposed to eliminate the accuracy balance between parameters. Compared with the first two measurement methods, weak measurement method is based on the weak value amplification principle of an indirect measurement. Measurements are performed virtually without perturbing the quantum system, which does not lead the wave function to collapse, the weak value of the real and virtual part have different physical significance, The combination of weak measurement theory and non-Hermitian system also further improves the measurement sensitivity. Multi-parameter measurement uses quantum entanglement, quantum control and other quantum resources to make the measurement progress reach the Heisenberg limit, which is the current research hotspot in the field of precision measurement. Furthermore, we present a conjecture whether there will be multi-atomic mixing measurements based on atomic spin effects or ultra-high sensitivity measurement instruments with precision of fT or even aT by using other particles detection. Finally, several measurement methods are analyzed and compared with each other, and the development prospect of quantum precision measurement is forecasted.

2022, 71 (13): 130302.
doi: 10.7498/aps.71.20220890
Abstract +
Non-Hermitian systems have attracted much attention during the past few years, both theoretically and experimentally. The existence of non-Hermiticity can induce multiple exotic phenomena that cannot be observed in Hermitian systems. In this work, we introduce a new non-Hermitian system called the non-Hermitian mosaic dimerized lattice. Unlike the regular nonreciprocal lattices where asymmetric hoppings are imposed on every hopping term, here in the mosaic dimerized lattices the staggered asymmetric hoppings are only added to the nearest-neighboring hopping terms with equally spaced sites. By investigating the energy spectra, the non-Hermitian skin effect (NHSE), and the topological phases in such lattice models, we find that the period of the mosaic asymmetric hopping can influence the system’s properties significantly. For a system with real system parameters, we find that as the strength of asymmetric hopping increases, the energy spectra of the system under open boundary conditions will undergo a real-imaginary or real-complex transition. As to the NHSE, we find that when the period is odd, there appears no NHSE in the system and the spectra under open boundary conditions (OBCs) and periodic boundary conditions (PBCs) are the same (except for the topological edge modes under OBCs). If the period of the mosaic asymmetric hopping is even, the NHSE will emerge and the spectra under different boundary conditions exhibit distinctive structures. The PBC spectra form loop structures, indicating the existence of point gaps that are absent in the spectra under OBCs. The point gap in the PBC spectrum is shown to be the topological origin of the NHSE under OBCs, which also explains the NHSE in our mosaic dimerized lattices. To distinguish whether the bulk states of the system under OBCs are shifted to the left or right end of the one-dimensional lattice due to the NHSE, we define a new variable called the directional inverse participation ratio (dIPR). The positive dIPR indicates that the state is localized at the right end while the negative dIPR corresponds to the states localized at the left end of the one-dimensional lattice. We further study the topological zero-energy edge modes and characterize them by calculating the Berry phases based on the generalized Bloch Hamiltonian method. In addition, we also find that the topological edge modes with nonzero but constant energy can exist in the system. Our work provides a new non-Hermitian lattice model and unveils the exotic effect of mosaic asymmetric hopping on the properties of non-Hermitian systems.
2022, 71 (13): 131101.
doi: 10.7498/aps.71.20220842
Abstract +
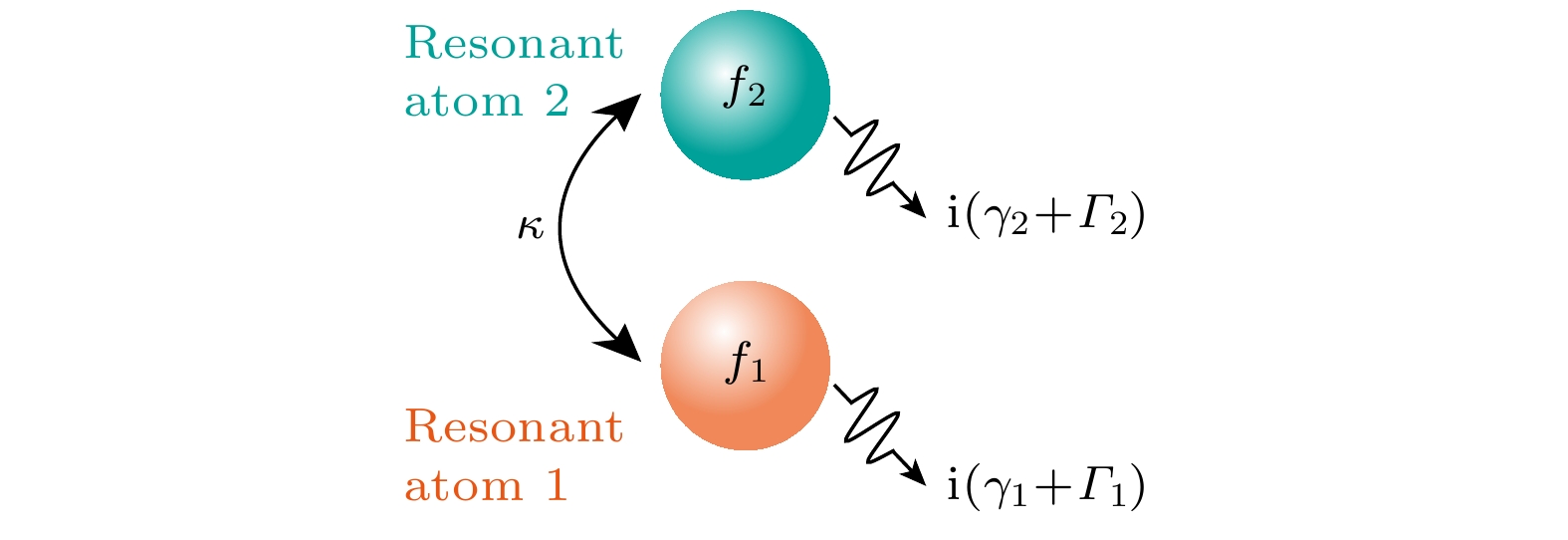
Based on the quantum mechanics, the physical observables are represented by Hermitian linear operators. Derived from the conservation of energy, these Hermitian operators exhibit real eigenvalues. However, when a closed system described by an effective Hamiltonian is coupled with the surrounding environment, the dynamics of the system itself becomes non-Hermitian dynamic. In general, the eigenvalues of an open optical non-Hermitian system are complex. Parity-time symmetric structure is the system composed of complex potentials, which is neither parity symmetric nor time reversal symmetric alone but is symmetric after operations of parity inversion and time reversal have been combined. The eigenvalue of the parity-time symmetric Hamiltonian can be found to be real, despite the non-Hermitian nature of the system. One of the most attractive properties of non-Hermitian system is the exceptional point, which is degenerate at which two or more eigenvalues and eigenstates of a non-Hermitian physical system coalesce. The unique topological features of EPs, forming a self-intersecting Riemann surface, have given rise to several exotic physical properties. As a kind of phase singularity in a physical system, exceptional point of non-Hermitian system gives rise to a plethora of counterintuitive phenomenon, such as the loss-induced transmission enhancement, unidirectional reflection and asymmetric state transfer. Especially, the eigenvectors of exceptional point are self-orthogonal and an inherent chirality can be determined because of the missing dimension. Chirality lies at the heart of the most fascinating and fundamental phenomena in modern physics, and how to impose a strong chirality and a switchable direction of light propagation in an optical system by steering it to an exceptional point is an interesting research topic. In this work, a non-Hermitian system is constructed based on the special metamaterial resonator of split-ring resonator, in which the sign of coupling coefficient can be flexibly controlled. Especially, the chiral inversion at an exceptional point of non-Hermitian system is observed experimentally. This sign of coupling coefficient controlled exceptional point not only paves a new way for studying the fundamental non-Hermitian physics in an open system, but also holds great potential in the applied photonic devices such as the efficient chiral mode converter and chiral antennas.

2022, 71 (13): 130303.
doi: 10.7498/aps.70.20220716
Abstract +
2022, 71 (13): 130301.
doi: 10.7498/aps.70.20220511
Abstract +
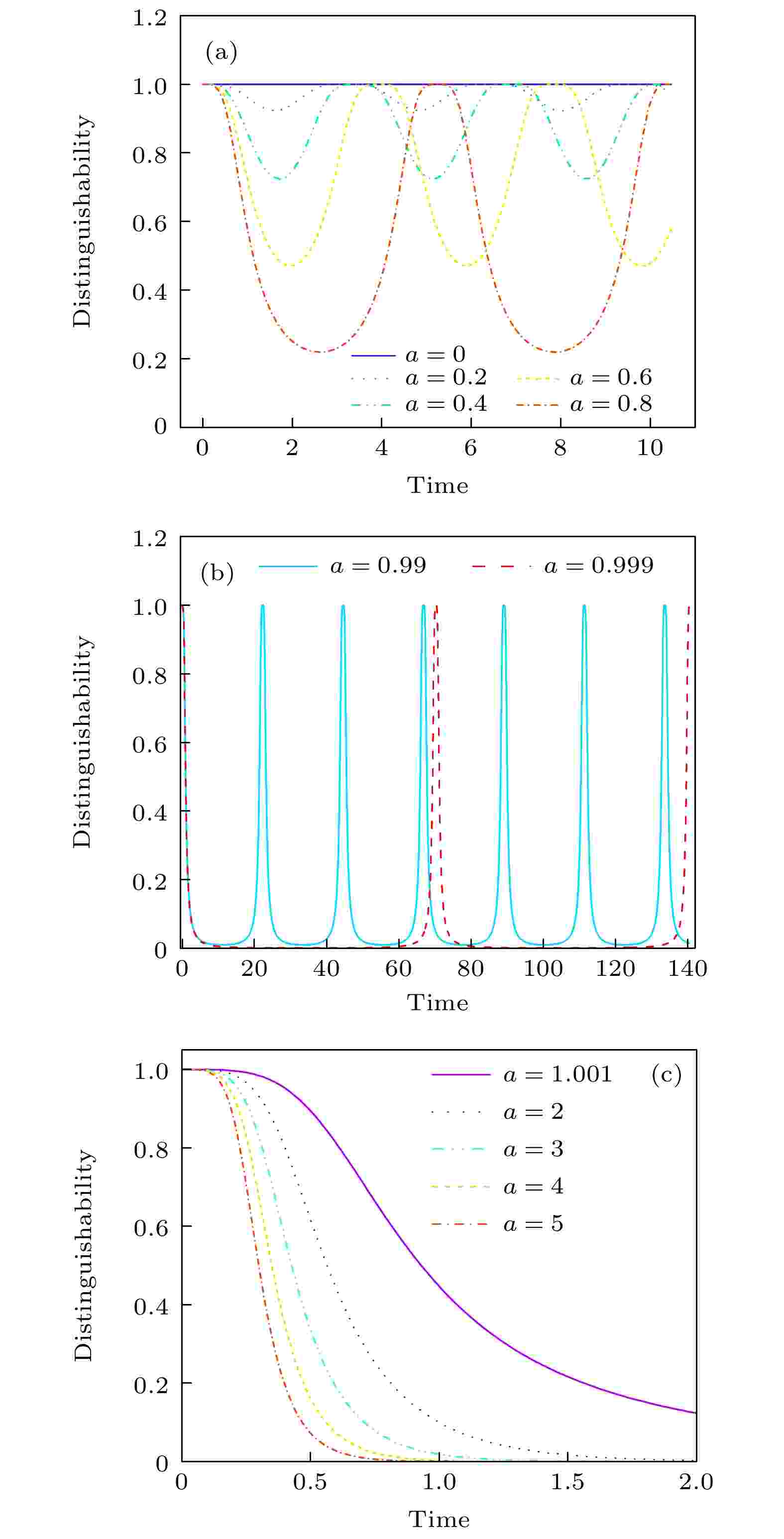
Recently, impressive progress has been made in the study of non-Hermitian systems with parity-time symmetry, such as observations of topological properties of physical systems and criticality at exceptional points. A crucial aspect of parity-time symmetric nonunitary dynamics is the information flow between the system and the environment. In this paper, we use the physical quantity, distinguishability between quantum states, to uniformly quantify the information flow between low-dimensional and high-dimensional parity-time symmetric non-Hermitian systems and environments. The numerical results show that the oscillation of quantum state distinguishability and complete information retrieval and can be obtained in the parity-time-unbroken phase. However, the information decays exponentially in the parity-time-broken phase. The exceptional point marks the criticality between reversibility and irreversibility of information flow, and the distinguishability between quantum states exhibits the behavior of power-law decay. Understanding these unique phenomena in nonunitary quantum dynamics provides an important perspective for the study of open quantum systems and contributes to their application in quantum information.
2022, 71 (13): 133202.
doi: 10.7498/aps.71.20220456
Abstract +
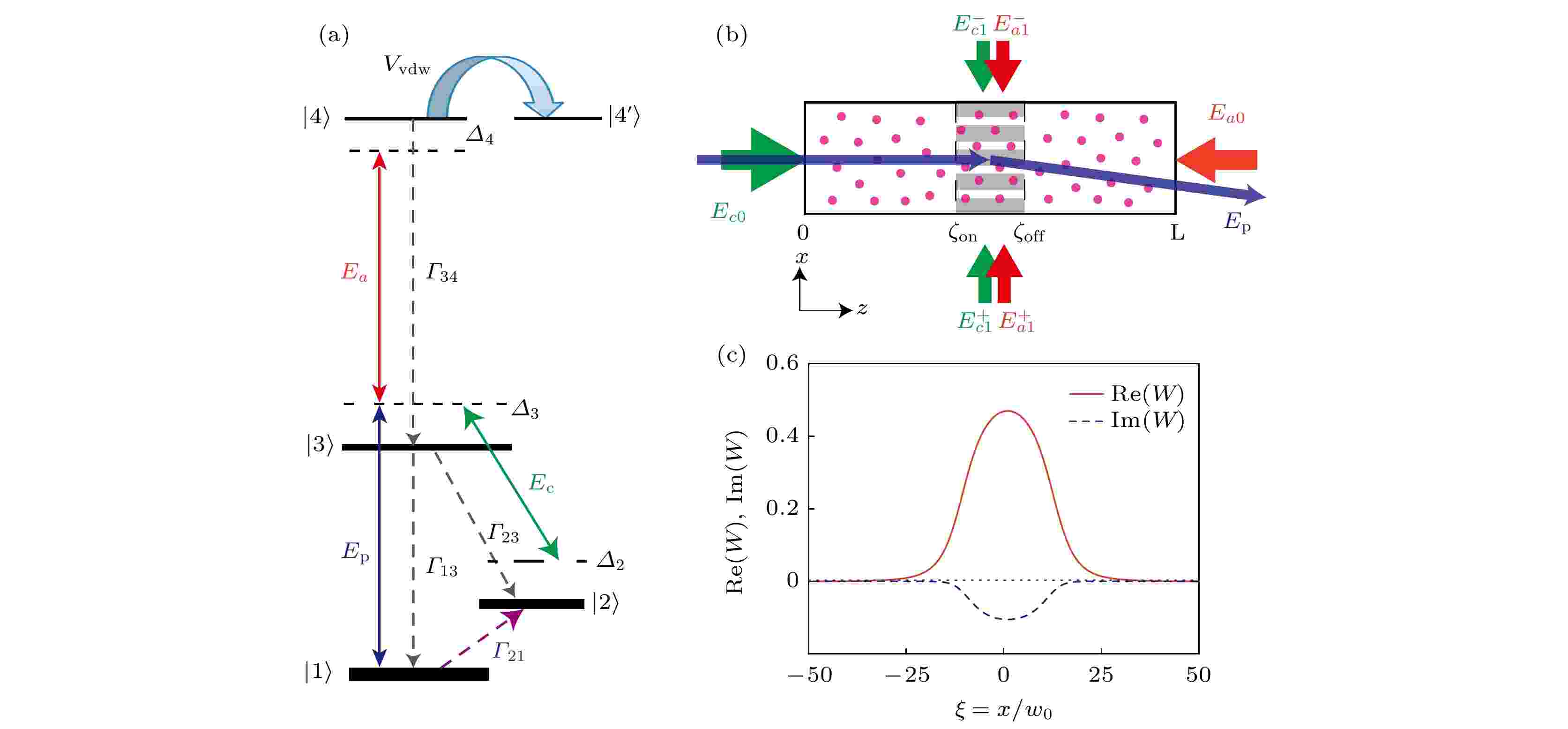
Based on a Rydberg-electromagnetically-induced-transparency (Rydberg-EIT) system, an electromagnetically induced grating (EIG) with parity-time (${\cal{PT}}$ ) symmetry is realized. The formation of solitons before the probe laser field reaching the EIG as well as its deflection when passing through the EIG are both investigated. It is found that due to the enhanced nonlinear optical effect of the Rydberg-EIT system, stable optical soliton can be formed with a very weak input light energy. In addition, it is found that by changing the gain/absorption coefficient of EIG, the period of EIG, and the nonlocality degree of optical Kerr nonlinear of the system, the deflection degree of the optical soliton can be effectively changed and manipulated. The research results of this work can provide a theoretical basis for the future applications of ${\cal{PT}}$ -symmetric EIG and may be useful in the fields of all-optical manipulation and optical information processing.

2022, 71 (17): 174201.
doi: 10.7498/aps.71.20220978
Abstract +
The application of energy band theory in optics provides an effective approach to modulating the flow of light. The recent discovery of non-Hermitian skin effect promotes the development of traditional energy band theory, which further enables an alternative way to realize light localization and unidirectional propagation. However, how to effectively generate and steer the non-Hermitian skin effect is still an important topic, especially in integrated optical systems. Here, we investigate the non-Hermitian skin effect in quasi-one-dimensional rhombic optical lattice with synthetic gauge potential. By calculating the eigenenergy spectra, spectral winding number, and wave dynamics, the gauge potential can be utilized to effectively tune the localization strength of skin modes. In particular, the skin effect is completely suppressed when the gauge potential in each plaquette is equal to π, while the flat-band localization caused by Aharonov-Bohm caging effect is dominant. By utilizing the indirectly coupled micro ring resonator array, the gauge potential and asymmetric coupling can be generated at the same time, which provides a potential experimental scheme to explore the competition between Aharonov-Bohm cage and skin effect. The present study provides an alternative way to steer the skin effect, which offers an approach to achieving the on-chip non-magnetic unidirectional optical devices.
2022, 71 (17): 170306.
doi: 10.7498/aps.71.20221087
Abstract +
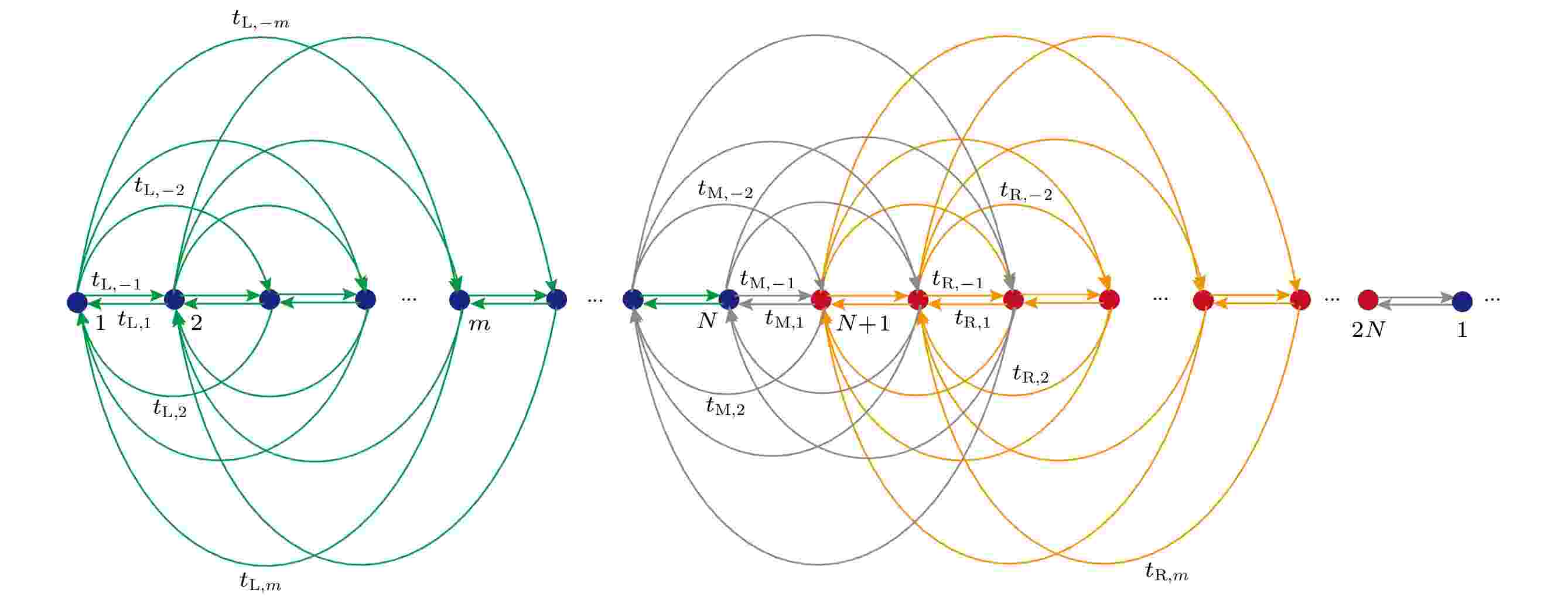
The non-Hermitian skin effect is one of the most striking features in non-Hermitian physics. It reveals a novel phenomenon in a non-Hermitian system that the bulk wave function and energy spectrum are sensitively dependent on the boundary conditions. The concept of generalized Brillouin zones has been proposed to characterize bulk wave functions in such systems . Based on generalized Brillouin zones, non-Bloch topological invariants can reconstruct the non-Hermitian bulk-edge correspondence. Previous discussion of the non-Hermitian skin effect mainly focused on open boundary conditions, and the calculation of generalized Brillouin zones needs to be reconsidered under domain-wall boundary conditions. The paper introduces the related researches of the non-Hermitian skin effect in domain-wall systems, including the general form of the generalized Brillouin zone equation in a one-dimensional single-band model, non-Bloch topological invariants in non-Hermitian SSH (Su-Schieffer-Heeger) model, and the experimental realization of the non-Hermitian skin effect in one-dimensional quantum walk system.

2022, 71 (17): 174501.
doi: 10.7498/aps.71.20220914
Abstract +
In recent years, two independent research fields, i.e. non-Hermitian andstrongly correlated systems have been merged, forming an important researchfield in physics. The progress of relevant theories and experiments hasreshaped our understanding of matter. In this field, the research object isnot limited to the influence of non-Hermiticity on the energy spectrum andthe eigenstate properties of many-body systems. Researchers have paid more attentionto the manipulation of quantum states. It is universally received that the exceptional point is the most significant featurethat distinguishes non-Hermitian quantum mechanics from Hermitian quantum mechanics. In addition to the recent advances in non-Hermitian topological band theory and quantum sensing around the exceptional points, this paper concentrates on the non-Hermitian critical dynamical phenomenon and its application to the quantum many-body system. When the system has an exceptional point, an arbitrary initial state belonging to the coalescent subspace will be projected on the coalescent state. Based on the directionality of the evolved quantum state, this paper reviews our several representative researches in recent years, including local-field-induced dynamical magnetization, quantum phase transition in transverse field, Ising model at non-zero temperature, quantum mold casting in the center-environment system, as well as superconducting state preparation in the non-Hermitian strongly correlated system. We also focus on the new preparation methods and detection schemes of non-equilibrium quantum states related to exception points.

2022, 71 (17): 170305.
doi: 10.7498/aps.71.20220862
Abstract +
Linear response theory is the theoretical foundation of modern experiments. In particular, it plays a vital role in measuring quantum matters. Its main idea is to take the external probe signal of the physical system as a perturbation and use the correlation function in the unperturbed equilibrium state to depict the response to the observable in system. In recent half century, the linear response theory for the closed quantum system has achieved great success in experiments on quantum matters. In recent years, with the tremendous progress of the precise manipulation of the light-matter interaction, the ultracold atom experiments can precisely control dissipative quantum many-body systems. With the discovery of many novel phenomena, dissipative quantum systems and non-Hermitian physics have attracted extensive attention in theory and experiment. We developed a linear response theory, named non-Hermitian linear response theory, to deal with open quantum systems. This theory takes the non-Hermitian term and quantum noise, which are induced by dissipation, as an external perturbative input, to detect the properties of the quantum system, and relates the time evolution of the observable with the correlation function in the unperturbed state of the system. The non-Hermitian linear response theory provides a new method for distinguishing the exotic quantum phase from the normal phase. The theoretical predictions are highly consistent with the recent experimental results of cold atom systems. This paper will review the non-Hermitian linear response theory and discuss its applications in quantum many-body and time-reversal symmetric quantum systems.

2022, 71 (17): 177302.
doi: 10.7498/aps.71.20220796
Abstract +
The topological property and the energy property of one-dimensional non-Hermitian spin-orbit-coupled Su-Schrieffer-Heeger (SSH) model are investigated theoretically, by introducing spin-dependent imaginary potentials with gain and loss effects. It is found that the imaginary potential leads the imaginary energy spectra to appera in the topologically nontrivial region of this system, and the ${\cal {PT}}$ phase transition to happen in the topologically trivial region. In addition, the imaginary potential energy and spin-orbit coupling work together to make the topological phase transition occur in the topologically trivial region, and the topological non-trivial region becomes wider. The energy spectrum results show that the imaginary potential energy and the spin-orbit coupling can obviously control the zero-energy states of the system, which mainly lies in the presence of four zero-energy states with four different localities and numbers. This shows the special adjustment effect of imaginary potential energy and spin-orbit coupling on the energy band structure of the system. It is believed that these results are helpful in understanding the topological phase transition behavior of ${\cal {PT}}$ -symmetric non-Hermitian system.

2022, 71 (17): 171101.
doi: 10.7498/aps.71.20221323
Abstract +
In standard quantum mechanics, the Hamiltonian describing the physical system is generally Hermitian, so as to ensure that the system has real energy spectra and that the system’s evolution is unitary. In recent years, it has been found that non-Hermitian Hamiltonians with parity-time (${\cal {PT}}$ ) symmetry also have real energy spectra, and there is a novel non-Hermitian exceptional point between ${\cal {PT}}$ -symmetric phase and ${\cal {PT}} $ -symmetry-broken phase, which is unique to non-Hermitian systems. Recently, people have realized ${\cal {PT}} $ symmetric and anti-${\cal {PT}}$ symmetric non-Hermitian Hamiltonians in various physical systems and demonstrated novel quantum phenomena, which not only deepened our understanding of the basic laws of quantum physics, but also promoted the breakthrough of application technology. This review will introduce the basic physical principles of ${\cal {PT}} $ symmetry and anti-${\cal {PT}}$ symmetry, summarize the schemes to realize ${\cal {PT}} $ symmetry and anti-${\cal {PT}} $ symmetry in optical and atomic systems systematically, including the observation of ${\cal {PT}} $ -symmetry transitions by engineering time-periodic dissipation and coupling in ultracold atoms and single trapped ion, the realization of anti-${\cal {PT}} $ symmetry in dissipative optical system by indirect coupling, and realizing anti-${\cal {PT}} $ -symmetry through fast atomic coherent transmission in flying atoms. Finally, we review the research on precision sensing using non-Hermitian exceptional points of ${\cal {PT}} $ -symmetric systems. Near the exceptional points, the eigenfrequency splitting follows an ${\varepsilon }^{\tfrac{1}{N}}$ -dependence, where the $\varepsilon$ is the perturbation and $ N $ is the order of the exceptional point. We review the ${\cal {PT}}$ -symmetric system composed of three equidistant micro-ring cavities and enhanced sensitivity at third-order exceptional points. In addition, we also review the debate on whether exceptional-point sensors can improve the signal-to-noise ratio when considering noise, and the current development of exceptional-point sensors, which is still an open and challenging question.

2022, 71 (24): 247802.
doi: 10.7498/aps.71.20221706
Abstract +
Electromagnetic metasurface, as a type of planar electromagnetic material consisting of single-layer or multilayer subwavelength artificial micro-structure, can efficiently control the polarization, amplitude and phase of electromagnetic wave on a subwavelength scale. However, confining electromagnetic waves to a deep-subwavelength scale generally is at the cost of a large loss, such as radiation loss, Ohmic loss. Interestingly, non-Hermitian physics provides us a new way to transform the disadvantage of loss into a new degree of freedom in metasurface design, paving the way to expanding the functionalities of metasurfaces. In recent years, the extraordinary effects in the non-Hermitian electromagnetic metasurfaces have attracted a lot of attention. In this review, we discuss the perfect absorption, exceptional points and surfaces waves of non-Hermitian electromagnetic metasurfaces, and point out the challenges and potentials in this field.


















