-
热电制冷技术是一种环保型的制冷技术, 具有广阔的应用前景. 其中Peltier效应在热电制冷过程中具有核心作用, 但是由于Peltier系数很难测量, 在实际应用过程中通常是首先得到Seebeck系数, 然后利用Kelvin第二关系式间接得到Peltier系数. 需要注意的是, Kelvin第二关系式是在线性条件下(Ohm定律、Fourier定律等)得到的, 而在实际过程中非线性的电流-电压关系(肖特基结、pn结等)和热输运关系却是大量存在的. 在纳米尺度, 量子效应将起到主导作用, 此时Peltier效应应该考虑非线性的影响, Kelvin第二关系式的适用性也应该重新考虑. 本文综述了采用不同方法对Peltier系数和Kelvin第二关系式的理论推导, 讨论了推导过程中利用的假设条件; 概述了Peltier系数实验测定的几种方法, 讨论了各种附加效应对Peltier系数测定的影响; 并介绍了非线性Peltier效应的理论工作. 最后本文讨论了在非线性条件下Peltier效应的研究策略和可行方向.
-
关键词:
- 非线性 /
- Peltier效应 /
- Kelvin第二关系式 /
- 热电制冷
Thermoelectric refrigeration technology is an environment-friendly refrigeration technology with broad application prospects. The Peltier effect plays a central role in the thermoelectric refrigeration process, however, the Peltier coefficient is difficult to measure. So in the actual application process, first, the Seebeck coefficient is usually obtained, and then the Peltier coefficient is achieved by the Kelvin's second relation indirectly. It should be noted that the Kelvin's second relation is obtained under linear conditions (Ohm's law, Fourier's law, etc.), while in practice, nonlinear current-voltage relationships (Schottky junction, pn junction, etc.) and nonlinear heat transport relations are common. And quantum effect plays a leading role in the nano-scaled region, then the Peltier effect must consider the influence of nonlinearity, and the applicability of the Kelvin's second relation must also be reconsidered. This paper first summarizes the theoretical derivation of Peltier coefficient and the Kelvin’s second relation by different methods, then discusses the hypothetical conditions used in the derivation process, and points out that the Kelvin’s second relation can be established only under the hypothetical linear conditions. Then, several experimental methods of determining the Peltier coefficient are summarized. It is found that there are still many problems encountered in the measurement of Peltier coefficient, and the Kelvin’s second relation has not been proved accurately by practical experiments. Various side effects (Fourier effect, Thomson effect, Joule effect and Seebeck effect) in the measurement process affect the temperature distribution of the system directly or indirectly, making it difficult to measure Peltier heat. After that, the theoretical work of nonlinear Peltier effect is briefly introduced. In the process of thermal transport and electrical transport on a microscopic scale, quantum effect plays a leading role, and the nonlinear part of the Peltier coefficient gradually emerges. These studies show the cognition of researchers that the Peltier effect gradually changes from linear to nonlinear. The nonlinear Peltier effect not only exists objectively, but also is very important in the practical applications. However, the current research on the nonlinear Peltier effect is still at the theoretical level, and there is almost no experimental work. Finally, we discuss the research strategy and feasible research direction of Peltier effect under nonlinear conditions. An integrated study of the relationship among various heterojunction band structures, interface properties and interface effects is helpful in comprehensively understanding the Peltier effect. With the continuous improvement of experimental conditions and theoretical research, the study of nonlinear Peltier effect is expected to realize a new breakthrough.[1] Peltier J C A 1834 Annales de Chimie et de Physique 56 371
[2] Disalvo F J 1999 Science 285 703
 Google Scholar
Google Scholar
[3] Bell L E 2008 Science 321 1457
 Google Scholar
Google Scholar
[4] He W, Zhang G, Zhang X, Ji J, Li G, Zhao X 2015 Appl. Energ. 143 1
 Google Scholar
Google Scholar
[5] Twaha S, Zhu J, Yan Y, Li B 2016 Renew. Sust. Energ. Rev. 65 698
 Google Scholar
Google Scholar
[6] He R, Schierning G, Nielsch K 2018 Adv. Mater. Technol. 3 1700256
 Google Scholar
Google Scholar
[7] Chowdhury I, Prasher R, Lofgreen K, Chrysler G, Narasimhan S, Mahajan R, Koester D, Alley R, Venkatasubramanian R 2009 Nat. nanotechnol. 4 235
 Google Scholar
Google Scholar
[8] Ibañez-Puy M, Bermejo-Busto J, Martín-Gómez C, Vidaurre-Arbizu M, Sacristán-Fernández J A 2017 Appl. Energ. 200 303
 Google Scholar
Google Scholar
[9] Hou W, Nie X, Zhao W, Zhou H, Mu X, Zhu W, Zhang Q 2018 Nano Energy 50 766
 Google Scholar
Google Scholar
[10] Caswell A E 1911 Phys. Rev. (Series I) 33 379
 Google Scholar
Google Scholar
[11] Rötzer G, Lockwood L, Gil Z J L 1977 J. Appl. Phys. 48 750
 Google Scholar
Google Scholar
[12] Fukushima A, Kubota H, Yamamoto A, Suzuki Y, Yuasa S 2006 J. Appl. Phys. 99 08H706
 Google Scholar
Google Scholar
[13] Garrido J 2009 J. Phys. Condens. Matter 21 155802
 Google Scholar
Google Scholar
[14] Garrido J, Casanovas A 2012 J. Electron. Mater. 41 1990
 Google Scholar
Google Scholar
[15] Avery A D, Zink B L 2013 Phys. Rev. Lett. 111 126602
 Google Scholar
Google Scholar
[16] Garrido J, Casanovas A 2014 J. Appl. Phys. 115 123517
 Google Scholar
Google Scholar
[17] Thomson W 1857 P. Roy. Soc. Edinb. 91
 Google Scholar
Google Scholar
[18] Callen H B 1948 Phys. Rev. 73 1349
 Google Scholar
Google Scholar
[19] Ioffe A F 1957 Semiconductor Thermoelements and Thermoelectric Cooling (London: Infosearch Limited) pp18−21
[20] Heikes R R, Ure R W 1961 Thermoelectricity: Science and Engineering (New York-London: Inderscience Publishers) pp40−42
[21] Zebarjadi M, Esfarjani K, Shakouri A 2007 Appl. Phys. Lett. 91 122104
 Google Scholar
Google Scholar
[22] Whitney R S 2013 Phys. Rev. B 88 064302
 Google Scholar
Google Scholar
[23] López R, Sánchez D 2013 Phys. Rev. B 88 045129
 Google Scholar
Google Scholar
[24] Bogachek E N, Scherbakov A G, Landman U 1998 Solid State Commun. 108 851
 Google Scholar
Google Scholar
[25] Drebushchak V A 2007 J. Therm. Anal. Calorim. 90 289
 Google Scholar
Google Scholar
[26] Drebushchak V A 2008 J. Therm. Anal. Calorim. 91 311
 Google Scholar
Google Scholar
[27] Onsager L 1931 Phys. Rev. 37 405
 Google Scholar
Google Scholar
[28] Wang C, Chen S 2009 J. Electron. Mater. 38 655
 Google Scholar
Google Scholar
[29] Straube H, Wagner J M, Breitenstein O 2009 Appl. Phys. Lett. 95 052107
 Google Scholar
Google Scholar
[30] Jin W, Liu L, Yang T, Shen H, Zhu J, Xu W, Li S, Li Q, Chi L, Di C A, Zhu D 2018 Nat. Commun. 9 3586
 Google Scholar
Google Scholar
[31] Titov O Y, Velazquez-Perez J E, Gurevich Y G 2015 Int. J. Therm. Sci. 92 44
 Google Scholar
Google Scholar
[32] Apertet Y, Goupil C 2016 Int. J. Therm. Sci. 104 225
 Google Scholar
Google Scholar
[33] Sánchez D, López R 2016 C. R. Phys. 17 1060
 Google Scholar
Google Scholar
[34] Kulik I O 1994 J. Phys. Condens. Matter 6 9737
 Google Scholar
Google Scholar
[35] Bogachek E N, Scherbakov A G, Landman U 1999 Phys. Rev. B 60 11678
 Google Scholar
Google Scholar
[36] Çipiloğlu M A, Turgut S, Tomak M 2004 Phys. Status Solidi B 241 2575
 Google Scholar
Google Scholar
[37] Zebarjadi M, Esfarjani K, Shakouri 2008 8th Symposium on Thermoelectric Power Generation Held 2007 MRS Fall Meeting Boston, November 26−29, 2007 p427
[38] Sadeghian R B, Bahk J-H, Bian Z, Shakouri A 2012 J. Electron. Mater. 41 1370
 Google Scholar
Google Scholar
-
图 2 线性与非线性现象的示意图 (a)线性的Ohm定律; (b)非线性的肖克莱方程式; (c)顺磁材料中磁感应强度与磁场强度的线性关系; (d)铁磁材料中磁感应强度与磁场强度的非线性关系; (e)顺电材料中电位移与电场强度的线性关系; (f)铁电材料中电位移与电场强度的非线性关系; (g)线性光学中极化强度与光场场强的线性关系; (h)非线性光学中极化强度与光场场强的非线性关系; (i)线性的Peltier效应; (j)非线性Peltier效应
Fig. 2. Schematic diagram of linear and nonlinear phenomena: (a) Linear Ohm's law; (b) nonlinear Shockley equation; (c) linear relationship between magnetic induction intensity and magnetic field intensity in paramagnetic materials; (d) nonlinear relationship between magnetic induction intensity and magnetic field intensity in ferromagnetic materials; (e) linear relationship between electric displacement and electric field intensity in paraelectric materials; (f) nonlinear relationship between electric displacement and electric field intensity in ferroelectric materials; (g) linear relationship between polarization intensity and optical field strength in linear optics; (h) nonlinear relationship between polarization intensity and optical field strength in nonlinear optics; (i) linear Peltier effect; (j) nonlinear Peltier effect.
图 3 由两种材料 (a, b)以及电压表组成的电路[18],
$ {T}_{1} $ 表示高温,$ {T}_{0} $ 表示低温,${T}'$ 表示环境温度,$ {\widetilde {\mu }}_{x} $ (x为0, 1, l, r)表示不同位置的电化学势Fig. 3. A circuit composed of two materials (a, b) and a voltmeter[18],
$ {T}_{1} $ represents high temperature,$ {T}_{0} $ represents low temperature,${T}'$ represents ambient temperature, and$ {\widetilde {\mu }}_{x} $ (x is 0, 1, l, r) represents electrochemical potential at different positions.图 4 两种材料 (a, b)组成的界面处Peltier效应示意图[18],
$ {{{w}}}_{{\rm{a}}\left({\rm{b}}\right)} $ 表示材料a(b)中的能量流密度,$ {{{q}}}_{\rm{a}}-{{{q}}}_{\rm{b}} $ 表示界面处吸收(放出)的Peltier热量Fig. 4. Schematic diagram of the Peltier effect at the interface composed of two materials (a, b)[18],
$ {{{w}}}_{{\rm{a}}\left({\rm{b}}\right)} $ represents the energy flow density in material a(b), and$ {{{q}}}_{\rm{a}}-{{{q}}}_{\rm{b}} $ represents the Peltier heat absorbed (released) at the interface.图 5 Seebeck效应和Peltier效应的能带原理图 (a)由金属-n型半导体-金属结构组成的器件在温度梯度下的能带结构; (b)由金属-n型半导体结构组成的器件在无外加电场下的能带结构
Fig. 5. Energy band principle diagrams of Seebeck effect and Peltier effect: (a) Energy band structure of a device composed of a metal-semiconductor (n-type)-metal structure under a temperature gradient; (b) energy band structure of a device composed of a metal-semiconductor (n-type) structure without an external electric field.
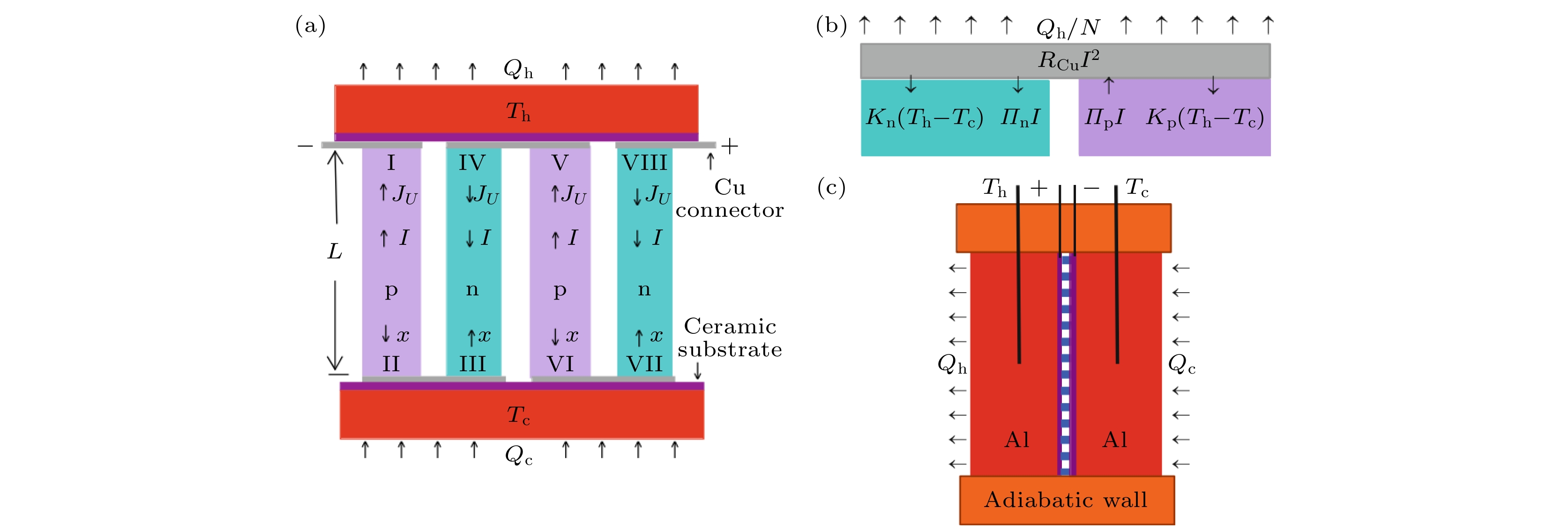
图 6 由n型和p型碲化铋半导体构成的热电器件[14] (a)由两对n/p热电对组成的热电器件; (b)一对n/p热电对的热端结构; (c)热电器件的侧面结构, 器件四周全部被绝热材料包覆, 只有两侧可以与外界换热
Fig. 6. Thermoelectric devices composed of n-type and p-type bismuth telluride semiconductors[14]: (a) A thermoelectric device composed of two pairs of n/p thermoelectric pairs; (b) hot end structure of a pair of n/p thermoelectric pairs; (c) side structure of the thermoelectric device, all around the device are covered with insulating materials, and only two sides can exchange heat with the outside world.
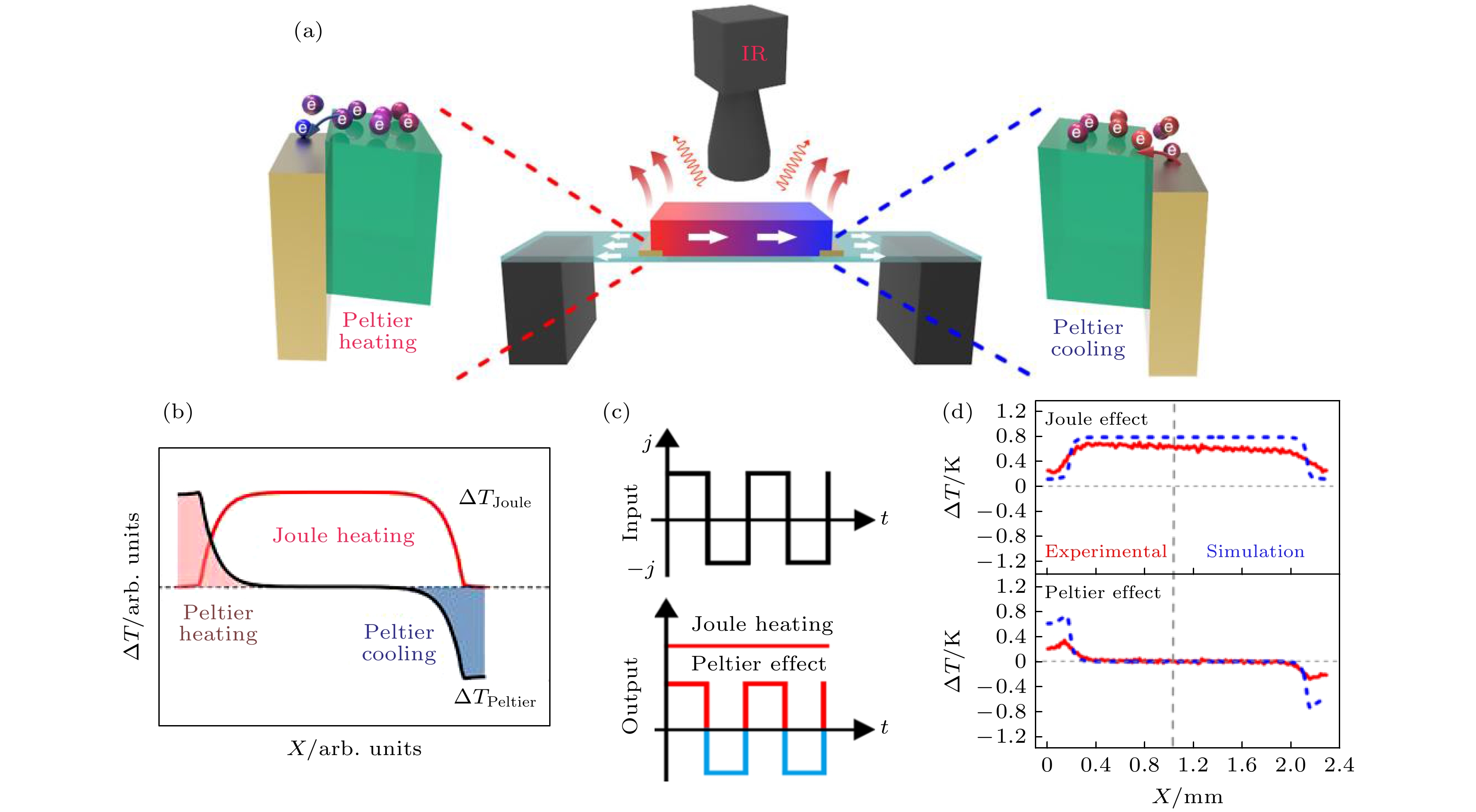
图 7 利用热悬浮装置和锁相热成像技术对有机薄膜中Peltier效应的测量[30] (a)在横向结构的薄膜热电器件上同时发生的热效应示意图; (b)由Joule热和Peltier热造成的温度分布示意图; (c)分离Joule热和Peltier热的机制示意图; (d)在电流密度为1.5 A/mm2, 施加时间为0.01 s时Peltier热和Joule热导致的温度分布
Fig. 7. Measurement of the Peltier effect in organic thin films using thermal levitation devices and lock-in thermal imaging technology[30]: (a) Schematic diagram of the thermal effects simultaneously occurring on the thin-film thermoelectric device with lateral structure; (b) temperature distribution caused by Joule heat and Peltier heat; (c) mechanism of separating Joule heat and Peltier heat; (d) temperature distribution caused by Peltier heat and Joule heat when current density is 1.5 A/mm2 and application time is 0.01 s.
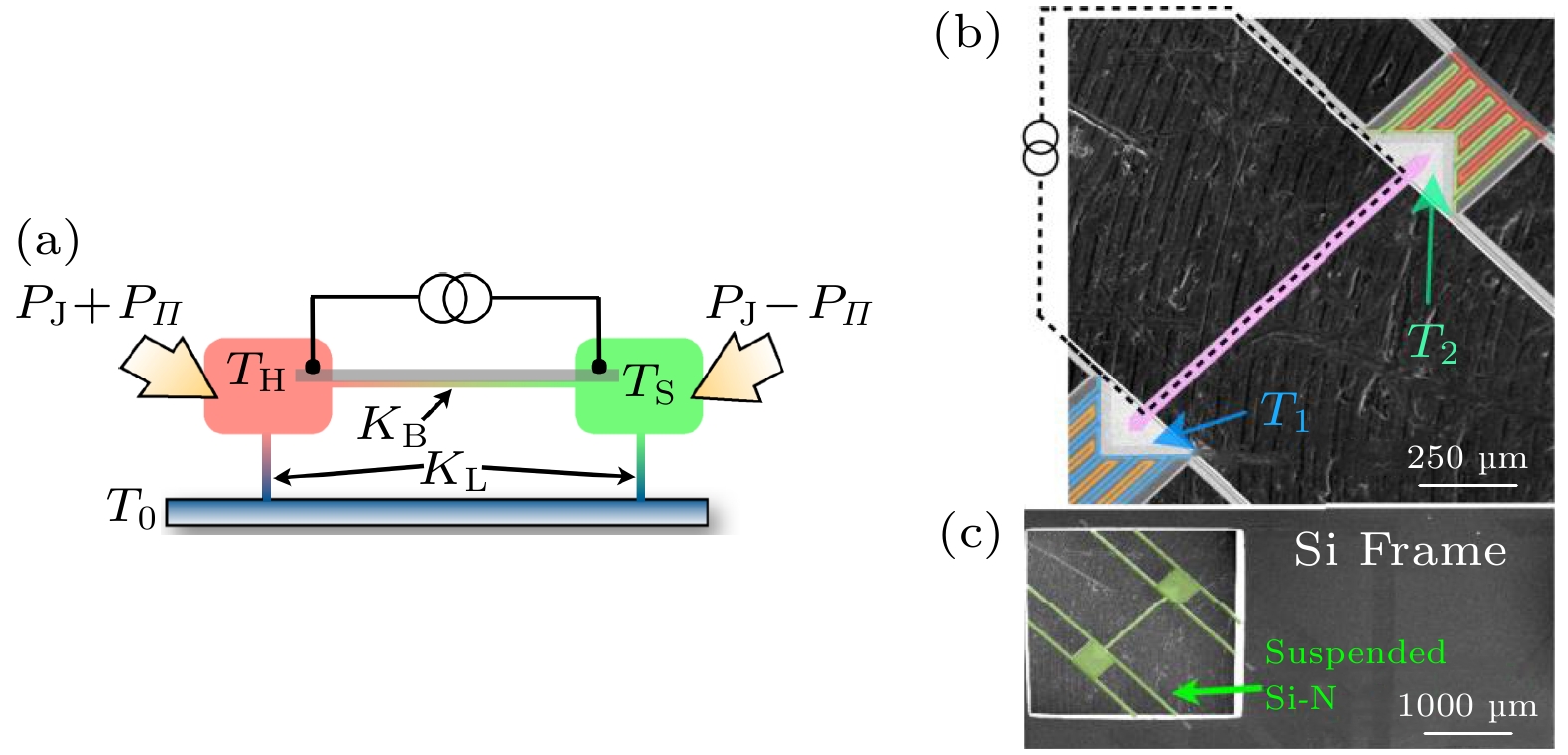
图 8 悬浮磁性薄膜的Peltier效应测试装置[15] (a)测试装置的侧面示意图; (b)测试装置的SEM图, 其中粉色表示样品, 红色和黄色表示加热器, 蓝色和绿色表示热电偶; (c)测试装置的局部放大SEM图
Fig. 8. Peltier effect test device of suspended magnetic film[15]: (a) Side view of the test device; (b) SEM image of the test device, in which pink represents the sample, red and yellow represent heaters, and blue and green represent thermocouples; (c) a partial enlarged SEM image of the test device.
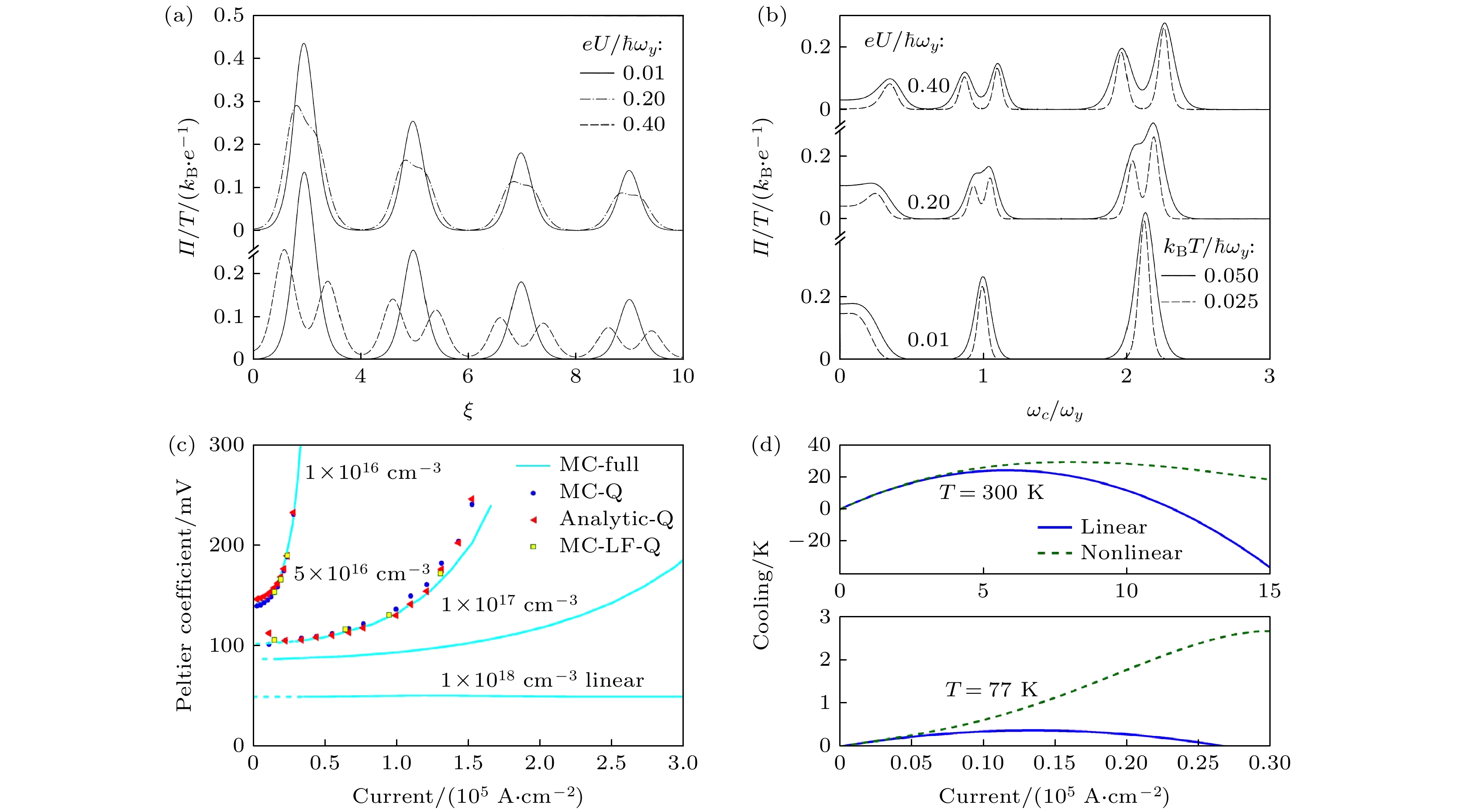
图 9 (a)在量子点接触时, 不同电压下,
$ \varPi /T $ 与$ {\rm{\xi }} $ 的关系图[24],$ {\rm{\xi }}=2\left(E-{\rm{e}}{U}_{0}\right)/\hslash {\omega }_{y} $ ; (b)当$ \xi =7 $ , 在不同电压和温度下$ \varPi /T $ 与无量纲回旋频率$ {\omega }_{\rm{c}}/{\omega }_{y} $ 的关系图[24]; (c)在掺杂InGaAs半导体中, 不同载流子浓度下, Peltier系数与电流的关系图[21]; (d)在77 K和300 K时, 非线性和线性Peltier效应产生的制冷性能与电流的关系图[21]Fig. 9. (a) In quantum dots, the relationship between
$ \varPi /T $ and$ {\rm{\xi }} $ under different voltages,$ {\rm{\xi }}=2\left(E-{\rm{e}}{U}_{0}\right)/\hslash {\omega }_{y} $ [24]; (b) when$ \xi =7 $ , the relationship between$ \varPi /T $ and the dimensionless cyclotron frequency$ {\omega }_{\rm{c}}/{\omega }_{y} $ at different voltages and temperatures[24]; (c) in doped InGaAs semiconductors, the relationship between Peltier coefficient and current under different carrier concentrations[21]; (d) at 77 K and 300 K, the relationship between current and cooling generated by the nonlinear and linear Peltier effect[21].表 1 物理符号命名
Table 1. Physical symbol nomenclature.
Q 热量(J) $ \bar {l} $ 电子平均自由程(m) $ {Q}_{\rm{P}} $ Peltier热(J) G 吉布斯自由能(J) $ {Q}_{\rm{T}} $ Thomson热(J) H 焓(J) I 电流(A) S 熵(J/K) U 电压(V) Δq 形成静电电压的电荷差值 i 电流密度(A/m2) a 电子热容系数(J/K) E 电场强度(V/m) N 电子总数 T 绝对温度(K) A 热电臂的横截面积(m2) Ji 通量, 代指热通量或电通量等 K 热导系数(W/K) Xj 引起迁移的广义力或动力 R 电热导率(S/m) Lij 唯象系数 $ {P}_{\rm{J}} $ Joule热功率密度(W/m3) J 粒子流密度 $ {P}_{\rm{P}} $ Peltier热功率密度(W/m3) q 热流密度(W/m2) m 电子有效质量(kg) S 熵流密度(W/(K·m2)) w 能量流密度(W/m2) 希腊字母 W 能量通量(W) $ \varPi $ Peltier系数(V) Is 熵流(W/K) $ \alpha $ Seebeck系数(V/K) E 电子能量(eV) $ {\sigma }_{\rm{T}} $ Thomson系数(V/K) $ {E}_{\rm{F}} $ 费米能级(eV) φ 接触电势(V) $ {E}_{\rm{c}} $ 导带底(eV) $ \widetilde {\mu } $ 电化学势, 参照文献[19, 20], 代表材料费米能级到真空能级的能量差(eV) $ {E}_{{\rm{v}}} $ 价带顶(eV) μ 化学势, 参照文献[19, 20], 代表费米能级到导带底的能量差(eV) $ \Delta {E}_{\rm{tn}} $ 在半导体中相对于导带底, 输运电子的平均能量(eV) ε 电子动能(eV) $ \Delta {E}_{\rm{m}} $ 在金属中相对于费米能级, 输运电子的平均能量(eV) $ \gamma $ 金属之间电子转移数目相关的系数 n 载流子浓度 ΘV 特征温度(K) r 散射因子 κ 热导率(W/(m·K)) D 扩散系数(m2/s) Γ 热转移系数(W/K) u 迁移率(m2/(V·s)) $ \sigma $ 电导率(S/m) k 玻尔兹曼常数 $ \tau $ 弛豫时间(s) h 普朗克常数 $ {\tau }_{i} $ 非弹性弛豫时间(s) $ \hslash $ 约化普朗克常数 $ \tau \left(E\right)$ 描述分布函数如何弛豫的特征时间(s) 表 2 不同方法对Seebeck系数、Peltier系数以及Kelvin第二关系式推导时的假设条件及存在的问题
Table 2. The assumptions and problems in the derivation of Seebeck coefficient, Peltier coefficient and Kelvin's second relationship by different methods.
理论 假设条件 存在问题 疑问 经典热力学推导 三种热电效应可逆 忽略Joule热和Fourier热 Peltier效应线性可逆(Peltier系数与
电流无关)Joule热和Fourier
热不可忽略Peltier系数真
的与电流无
关吗?不可逆热力学推导 控制不可逆过程的宏观规律可以用线性形式 Onsager倒易关系 非线性关系大量存在(如pn结中的电流-电压关系) Onsager倒易关系只适用于线性条件 能带理论
推导爱因斯坦关系式 界面处由于费米能级的不连续性导致的电子跃迁放热归结为Joule热 爱因斯坦关系式是一种线性关系 界面处电子跃迁引起的热量变化似乎和Peltier效应更为类似 吉布斯函数推导 热力学平衡态 有温度梯度存在时则不能将其考虑成热力学平衡态 表 3 不同材料的Seebeck系数与Peltier系数
Table 3. Seebeck coefficient and Peltier coefficient of different materials.
研究对象 测试温度/K Seebeck系数/mV·K–1 $ \alpha T $/mV Peltier系数/mV 文献 金属 Cu/Bi热电偶 300 $ {\alpha }_{\rm{Bi}}-{\alpha }_{\rm{Cu}} $ 0.0548 16.4 $ {\varPi }_{\rm{Bi}}-{\varPi }_{\rm{Cu}} $ 16 [10] 镍铝/镍铬合金热电偶 310 $ {\alpha }_{\rm{ch}}-{\alpha }_{\rm{al}} $ 0.0406 12.6 $ {\varPi }_{\rm{ch}}-{\varPi }_{\rm{al}} $ 27.2±1.3 [16] Co/Au热电偶 295 $ {\alpha }_{\rm{Au}}-{\alpha }_{\rm{Co}} $ 0.0329 9.7 $ {\varPi }_{\rm{Au}}-{\varPi }_{\rm{Co}} $ 27 [12] 半导体 p型硅的固液界面 1683 — — — $ {\varPi }_{\text{固}}-{\varPi }_{\text{液}} $ 190±25% [11] 碲化铋半导体 300 $ {\alpha }_{\rm{p}}-{\alpha }_{\rm{n}} $ 0.420 126 $ {\varPi }_{\rm{p}}-{\varPi }_{\rm{n}} $ 124±0.7 [14] 薄膜 悬浮的Ni-ett 300 ${\alpha _{ {\rm{poly} }\left( { {\rm{Ni} }\text-{\rm{ett} } } \right)} }$ –0.079 –23.5 ${\varPi _{{\rm{poly}}\left( {{\rm{Ni}} \text- {\rm{ett}}} \right)}} $ –21.6 [30] 悬浮的磁性薄膜 300 $ {\alpha }_{\rm{Fe}} $ 0.0062 1.86 $ {\varPi }_{\rm{Fe}} $ 1.81 [15] 300 $ {\alpha }_{\rm{Ni}} $ –0.015 –4.50 $ {\varPi }_{\rm{Ni}}$ 3.89 [15] 300 ${\alpha }_{ {\rm{Ni} }\text-{\rm{Fe} } }$ –0.023 –6.90 ${\varPi }_{ {\rm{Ni} }\text-{\rm{Fe} } }$ –6.50 [15] 表 4 非线性Peltier效应的理论进展总结
Table 4. Summary of the theoretical progress of the nonlinear Peltier effect.
研究人员 研究对象 主要结论 Kulik[34] 金属膜 $\varPi =\dfrac{ {\text{π} }^{2}{T}^{2} }{2{\rm{e} }\mu }+\dfrac{3{\text{π} }^{2}{\rm{e} }\tau {\tau }_{\rm{i} } }{m}{\left|{{E} }\right|}^{2}$, 在低温时, Peltier效应的线性部分随温度的降低而逐渐消失, 非线性部分将变为主导 López等[23] 量子点接触 $\varPi ={\varPi }_{1}\left[1+\dfrac{1}{ {\sigma }_{11} }\left(\dfrac{ {R}_{111} }{ {R}_{11} }-\dfrac{ {\sigma }_{111} }{ {\sigma }_{11} }\right)I+\cdots \right]$, Peltier系数的非线性部分由非线性传导系数与线性传导系数的相对强度以及导体的热特性和电特性之间的差值给出 Bogachek等[24] 量子点接触 $\varPi =T\dfrac{\partial {I}_{\rm{s} } }{\partial I}$, Peltier效应可能受到外加电压、垂直磁场或两者共同作用影响而呈现非线性 Çipiloğlu等[36] 量子点接触 非线性Peltier效应最低阶是三阶的 Zebarjadi等[21] 掺杂InGaAs半导体 $ \varPi ={\varPi }_{1}+{\varPi }_{3}{{{i}}}^{2} $, 三阶Peltier系数正比于电子有效质量, 反比于载流子浓度的平方, 在77 K时非线性Peltier效应将使制冷性能提高700% Sadeghian等[38] InAs1–xSbx半导体 300 K下非线性系统的最大冷却量是线性系统的两倍以上 -
[1] Peltier J C A 1834 Annales de Chimie et de Physique 56 371
[2] Disalvo F J 1999 Science 285 703
 Google Scholar
Google Scholar
[3] Bell L E 2008 Science 321 1457
 Google Scholar
Google Scholar
[4] He W, Zhang G, Zhang X, Ji J, Li G, Zhao X 2015 Appl. Energ. 143 1
 Google Scholar
Google Scholar
[5] Twaha S, Zhu J, Yan Y, Li B 2016 Renew. Sust. Energ. Rev. 65 698
 Google Scholar
Google Scholar
[6] He R, Schierning G, Nielsch K 2018 Adv. Mater. Technol. 3 1700256
 Google Scholar
Google Scholar
[7] Chowdhury I, Prasher R, Lofgreen K, Chrysler G, Narasimhan S, Mahajan R, Koester D, Alley R, Venkatasubramanian R 2009 Nat. nanotechnol. 4 235
 Google Scholar
Google Scholar
[8] Ibañez-Puy M, Bermejo-Busto J, Martín-Gómez C, Vidaurre-Arbizu M, Sacristán-Fernández J A 2017 Appl. Energ. 200 303
 Google Scholar
Google Scholar
[9] Hou W, Nie X, Zhao W, Zhou H, Mu X, Zhu W, Zhang Q 2018 Nano Energy 50 766
 Google Scholar
Google Scholar
[10] Caswell A E 1911 Phys. Rev. (Series I) 33 379
 Google Scholar
Google Scholar
[11] Rötzer G, Lockwood L, Gil Z J L 1977 J. Appl. Phys. 48 750
 Google Scholar
Google Scholar
[12] Fukushima A, Kubota H, Yamamoto A, Suzuki Y, Yuasa S 2006 J. Appl. Phys. 99 08H706
 Google Scholar
Google Scholar
[13] Garrido J 2009 J. Phys. Condens. Matter 21 155802
 Google Scholar
Google Scholar
[14] Garrido J, Casanovas A 2012 J. Electron. Mater. 41 1990
 Google Scholar
Google Scholar
[15] Avery A D, Zink B L 2013 Phys. Rev. Lett. 111 126602
 Google Scholar
Google Scholar
[16] Garrido J, Casanovas A 2014 J. Appl. Phys. 115 123517
 Google Scholar
Google Scholar
[17] Thomson W 1857 P. Roy. Soc. Edinb. 91
 Google Scholar
Google Scholar
[18] Callen H B 1948 Phys. Rev. 73 1349
 Google Scholar
Google Scholar
[19] Ioffe A F 1957 Semiconductor Thermoelements and Thermoelectric Cooling (London: Infosearch Limited) pp18−21
[20] Heikes R R, Ure R W 1961 Thermoelectricity: Science and Engineering (New York-London: Inderscience Publishers) pp40−42
[21] Zebarjadi M, Esfarjani K, Shakouri A 2007 Appl. Phys. Lett. 91 122104
 Google Scholar
Google Scholar
[22] Whitney R S 2013 Phys. Rev. B 88 064302
 Google Scholar
Google Scholar
[23] López R, Sánchez D 2013 Phys. Rev. B 88 045129
 Google Scholar
Google Scholar
[24] Bogachek E N, Scherbakov A G, Landman U 1998 Solid State Commun. 108 851
 Google Scholar
Google Scholar
[25] Drebushchak V A 2007 J. Therm. Anal. Calorim. 90 289
 Google Scholar
Google Scholar
[26] Drebushchak V A 2008 J. Therm. Anal. Calorim. 91 311
 Google Scholar
Google Scholar
[27] Onsager L 1931 Phys. Rev. 37 405
 Google Scholar
Google Scholar
[28] Wang C, Chen S 2009 J. Electron. Mater. 38 655
 Google Scholar
Google Scholar
[29] Straube H, Wagner J M, Breitenstein O 2009 Appl. Phys. Lett. 95 052107
 Google Scholar
Google Scholar
[30] Jin W, Liu L, Yang T, Shen H, Zhu J, Xu W, Li S, Li Q, Chi L, Di C A, Zhu D 2018 Nat. Commun. 9 3586
 Google Scholar
Google Scholar
[31] Titov O Y, Velazquez-Perez J E, Gurevich Y G 2015 Int. J. Therm. Sci. 92 44
 Google Scholar
Google Scholar
[32] Apertet Y, Goupil C 2016 Int. J. Therm. Sci. 104 225
 Google Scholar
Google Scholar
[33] Sánchez D, López R 2016 C. R. Phys. 17 1060
 Google Scholar
Google Scholar
[34] Kulik I O 1994 J. Phys. Condens. Matter 6 9737
 Google Scholar
Google Scholar
[35] Bogachek E N, Scherbakov A G, Landman U 1999 Phys. Rev. B 60 11678
 Google Scholar
Google Scholar
[36] Çipiloğlu M A, Turgut S, Tomak M 2004 Phys. Status Solidi B 241 2575
 Google Scholar
Google Scholar
[37] Zebarjadi M, Esfarjani K, Shakouri 2008 8th Symposium on Thermoelectric Power Generation Held 2007 MRS Fall Meeting Boston, November 26−29, 2007 p427
[38] Sadeghian R B, Bahk J-H, Bian Z, Shakouri A 2012 J. Electron. Mater. 41 1370
 Google Scholar
Google Scholar
计量
- 文章访问数: 21044
- PDF下载量: 311
- 被引次数: 0














 下载:
下载: