-
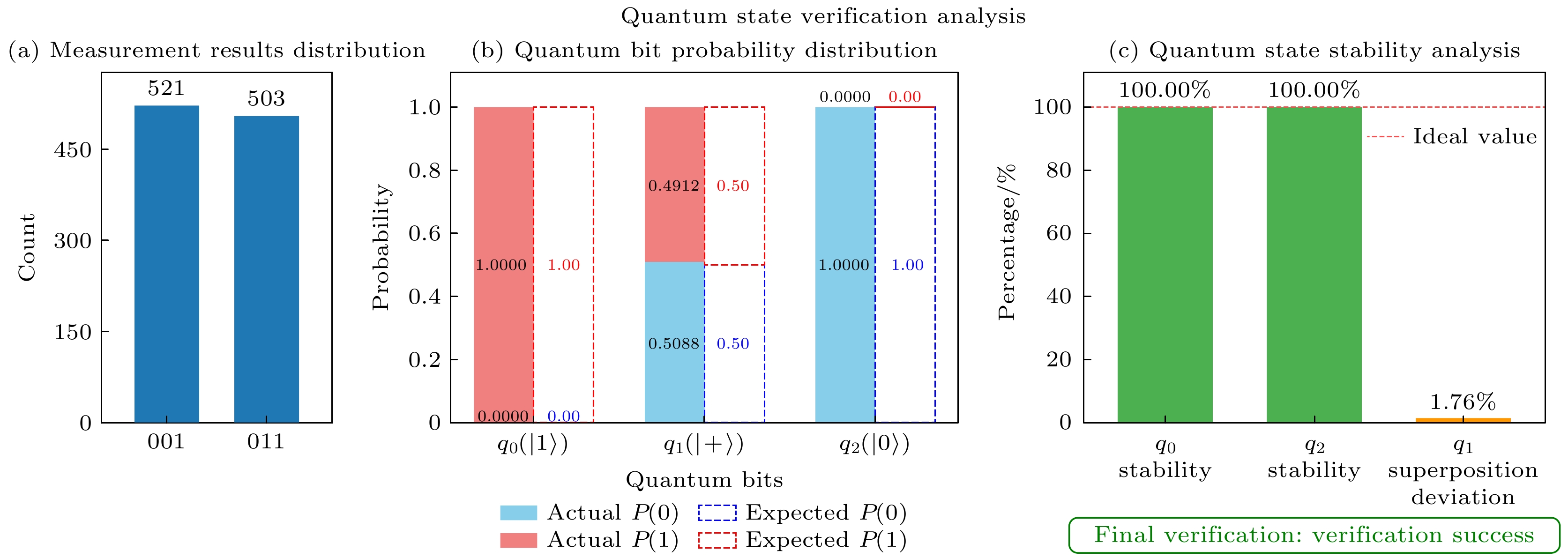
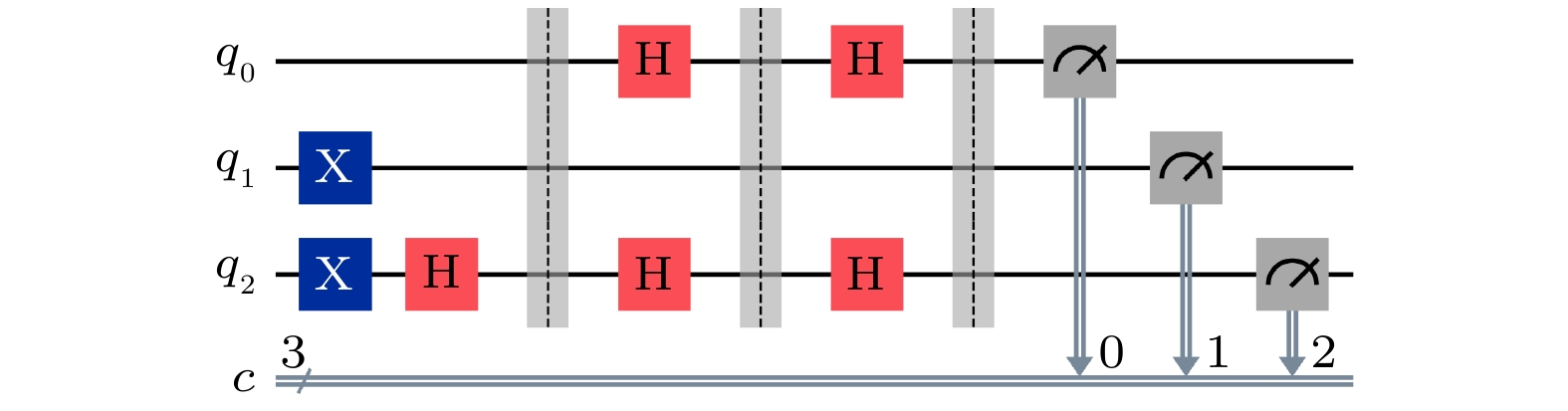
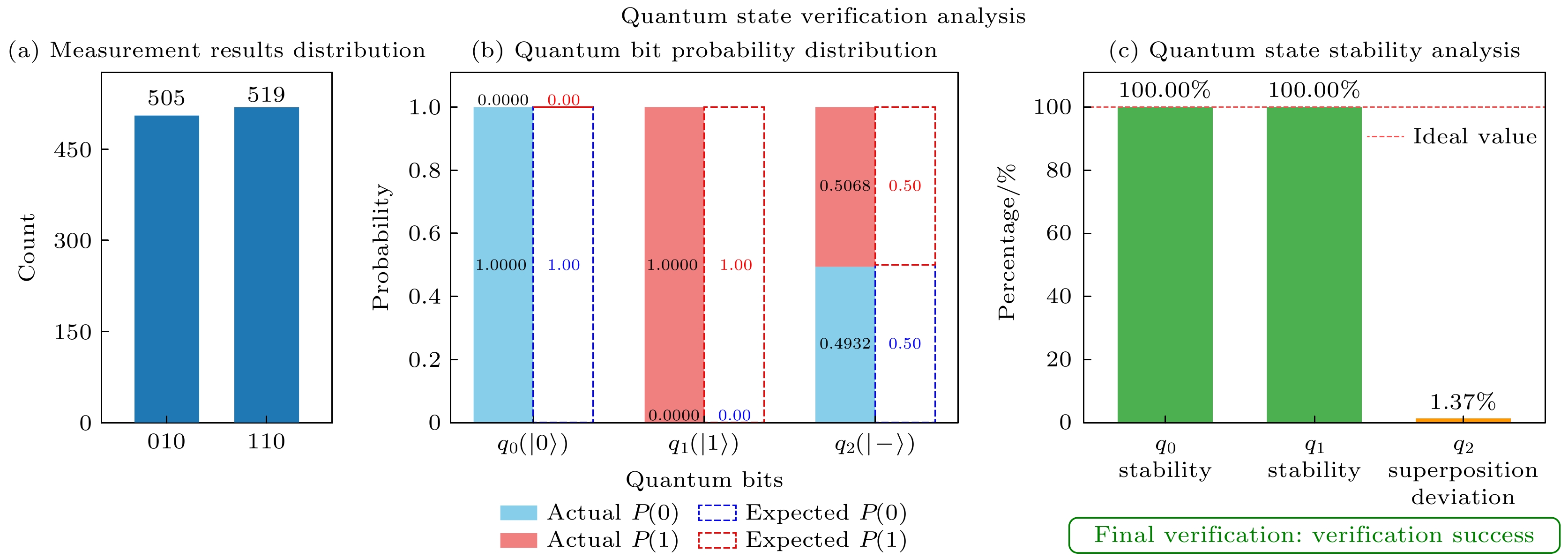
Quantum secret sharing (QSS) is a cryptographic protocol that utilizes fundamental principles of quantum mechanics to securely distribute and reconstruct secret information among multiple participants. Most existing protocols rely on entangled states (such as Bell and GHZ states), but in practical applications. The preparation of entangled state is constrained by a short quantum coherence time, low state fidelity, etc., which makes it difficult to implement entangled resource-dependent QSS protocols. In this work, a novel practical and verifiable multi-party QSS protocol is proposed based on orthogonal product states, which are easier to prepare than entangled states. During the protocol preparation stage, the secret distributor first converts pre-shared classical secret information into the corresponding orthogonal product states according to the encoding rules, and pre-shares a communication key with participants via quantum key distribution (QKD), which is used to hide the initial quantum sequence information through subsequent particle transformation operations. After preparing the orthogonal product states, the distributor reorganizes the particles by position, extracting particles at the same position from each state to form new sequences, shuffling their order, then applying Hadamard operations using a pre-shared key, inserting decoy particles, and sending the sequences to the participants. After receiving it, participants conduct eavesdropping detection, use the same key for the inverse transformations, retain one particle from each sequence, and sequentially pass the remaining particles until the last participant receives a complete set, triggering state verification with the arbiter distributor. If the verification is successful, the particles will be returned to the first participant and the return stage will follow the same procedure. Only after both the transmission and return stage verifications have passed, will the distributor reveal the initial particle positions, allowing participants to collaboratively reconstruct the secret. In the protocol, the secret distributor acts as an arbitrator to verify the particle state information together with participants at designated points (the end of the transmission stage and the end of the return stage) in order to determine whether the particle-state information is error-free during transmission. If the verification fails at either stage, the protocol will be terminated immediately. Meanwhile, considering that the number of participants may change during the execution of the protocol, a dynamic scheme for personnel changes is designed to ensure the flexibility of the protocol. Through the analysis of possible internal and external attacks, It can be proven that our protocol can effectively resist the existing common attack. Using Qiskit simulation experiments, the core quantum procedures of the protocol can be successfully modeled. The experimental results provide strong computational validation of the theoretical feasibility of the protocol.
-
Keywords:
- quantum secret sharing /
- verifiable /
- orthogonal product state /
- dynamic change
[1] Hellman M, Diffie W 1976 IEEE Trans. Inf. Theory 22 644
 Google Scholar
Google Scholar
[2] Fujisaki E, Okamoto T 1999 Annual international cryptology conference Santa Barbara, California, USA, August 15–19, 1999 p537
[3] Bellare M, Desai A, Jokipii E, Rogaway P 1997 Proceedings 38 th Annual Symposium on Foundations of Computer Science Miami Beach, FL, USA, October 20–22, 1997 p394
[4] Feistel H 1973 Sci. Amer. 228 15
[5] Shor P W 1999 SIAM Rev. 41 303
 Google Scholar
Google Scholar
[6] Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing Philadelphia, Pennsylvania, May 22–24, 1996 p212
[7] Bennett C H, Brassard G 1984 Proc. Workshop on the Theory and Application of Cryptographic Techniques Santa Barbara, California, USA, August 19–22, 1984 p475
[8] 冯发勇, 张强 2007 物理学报 4 1924
 Google Scholar
Google Scholar
Feng F Y, Zhang Q 2007 Acta Phys. Sin. 4 1924
 Google Scholar
Google Scholar
[9] Zhao Z, Chen Y A, Zhang A N, Yang T, Briegel H J, Pan J W 2004 Nature 430 54
 Google Scholar
Google Scholar
[10] Wang T Y, Wen Q Y 2011 Chin. Phys. B 20 040307
 Google Scholar
Google Scholar
[11] Jiang S X, Zhao B, Liang X Z 2021 Chin. Phys. B 30 060303
 Google Scholar
Google Scholar
[12] Deng F G, Long G L, Liu X S 2003 Phys. Rev. A 68 042317
 Google Scholar
Google Scholar
[13] 赵宁, 江英华, 周贤韬 2022 物理学报 71 150304
 Google Scholar
Google Scholar
Zhao N, Jiang Y H, Zhou X T 2022 Acta Phys. Sin. 71 150304
 Google Scholar
Google Scholar
[14] Deng F G, Zhou H Y, Long G L 2006 J. Phys. A: Math. Gen. 39 14089
 Google Scholar
Google Scholar
[15] 孙莹, 杜建忠, 秦素娟, 温巧燕, 朱甫臣 2008 物理学报 08 4689
 Google Scholar
Google Scholar
Sun Y, Du J Z, Qin S J, Wen Q Y, Zhu F C 2008 Acta Phys. Sin. 08 4689
 Google Scholar
Google Scholar
[16] Dai Y W, Qin H Y 2015 Chin. Phys. Lett. 32 100301
 Google Scholar
Google Scholar
[17] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
 Google Scholar
Google Scholar
[18] Karlsson A, Koashi M, Imoto N 1999 Phys. Rev. A 59 162
 Google Scholar
Google Scholar
[19] Xiao L, Lu Long G, Deng F G, Pan J W 2004 Phys. Rev. A 69 052307
 Google Scholar
Google Scholar
[20] Yang Y, Wen Q, Zhu F 2007 Sci. China Ser. G-Phys. Mech. Astron. 50 331
 Google Scholar
Google Scholar
[21] Wang T Y, Wen Q Y, Chen X B, Guo F Z, Zhu F C 2008 Opt. Commun. 281 6130
 Google Scholar
Google Scholar
[22] Wang C, Zhang Y 2009 Chin. Phys. B 18 3238
 Google Scholar
Google Scholar
[23] Jia H Y, Wen Q Y, Gao F, Qin S J, Guo F Z 2012 Phys. Lett. A 376 1035
 Google Scholar
Google Scholar
[24] Hsu J L, Chong S K, Hwang T, Tsai C W 2013 Quantum Inf. Process. 12 331
 Google Scholar
Google Scholar
[25] Du Y T, Bao W S 2018 Chin. Phys. B 27 080304
 Google Scholar
Google Scholar
[26] Yang C W, Tsai C W 2020 Quantum Inf. Process. 19 1
 Google Scholar
Google Scholar
[27] Hu W, Zhou R G, Li X, Fan P, Tan C 2021 Quantum Inf. Process. 20 1
 Google Scholar
Google Scholar
[28] Tian Y, Wang J, Bian G, Chang J, Li J 2024 Adv. Quantum Technol. 7 2400116
 Google Scholar
Google Scholar
[29] Lin J, Chen C C, Huang C Y 2024 Physica A 638 129615
 Google Scholar
Google Scholar
[30] Yu S, Oh C H 2015 arXiv: 1502.01274 [quant-ph]
[31] Guo G P, Li C F, Shi B S, Li J, Guo G C 2001 Phys. Rev. A 64 042301
 Google Scholar
Google Scholar
[32] Jiang D H, Wang J, Liang X Q, Xu G B, Qi H F 2020 Int. J. Theor. Phys. 59 436
 Google Scholar
Google Scholar
[33] Jiang D H, Hu Q Z, Liang X Q, Xu G B 2020 Int. J. Theor. Phys. 59 1442
 Google Scholar
Google Scholar
[34] Walgate J, Hardy L 2002 Phys. Rev. Lett. 89 147901
 Google Scholar
Google Scholar
[35] Xu G B, Wen Q Y, Qin S J, Yang Y H, Gao F 2016 Phys. Rev. A 93 032341
 Google Scholar
Google Scholar
[36] Feng Y, Shi Y 2009 IEEE Trans. Inf. Theory 55 2799
 Google Scholar
Google Scholar
[37] Deng F G, Li X H, Zhou H Y, Zhang Z J 2005 Phys. Rev. A 72 044302
 Google Scholar
Google Scholar
[38] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
 Google Scholar
Google Scholar
[39] Cabello A 2000 Phys. Rev. Lett. 85 5635
 Google Scholar
Google Scholar
-
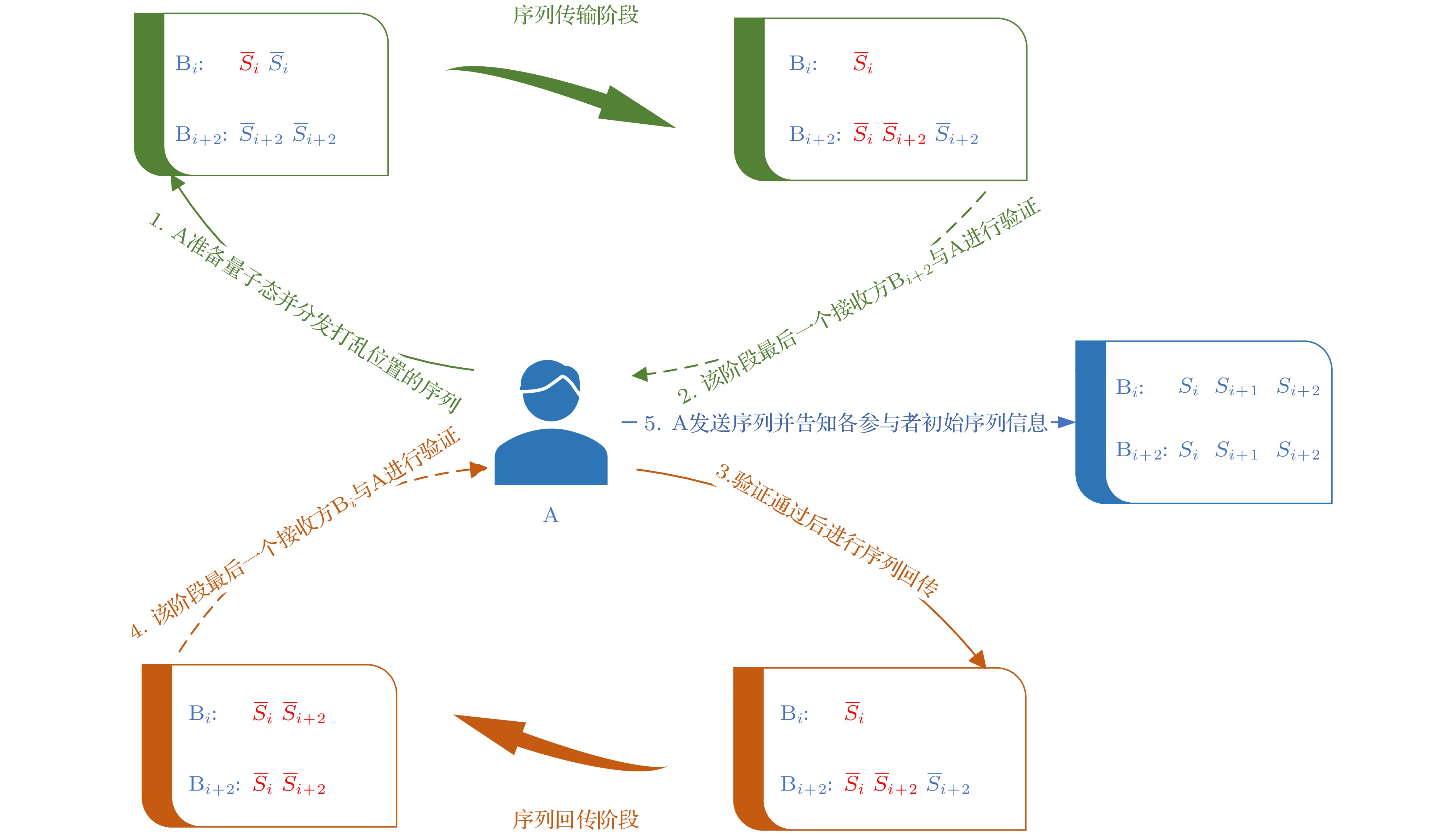
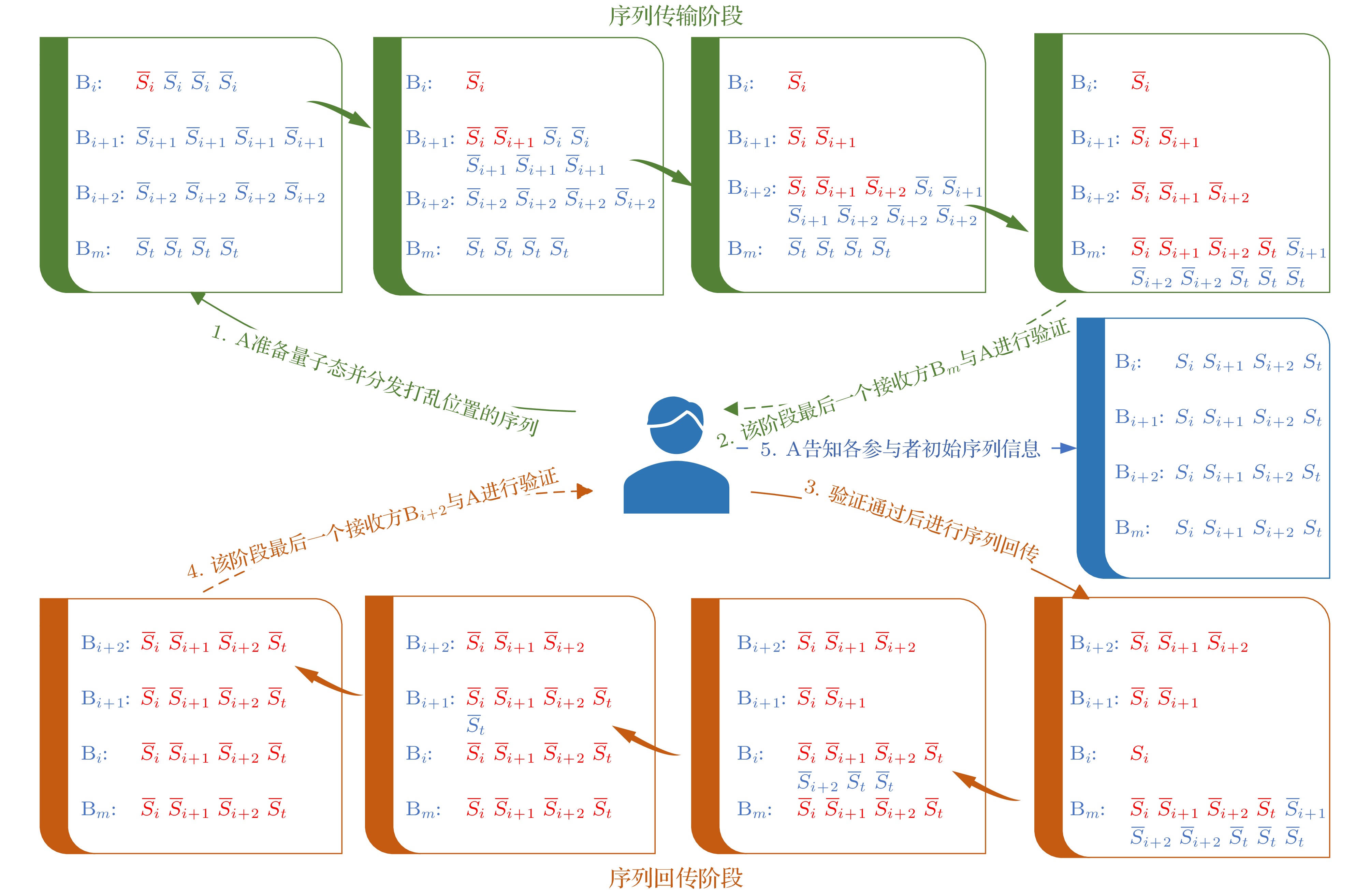
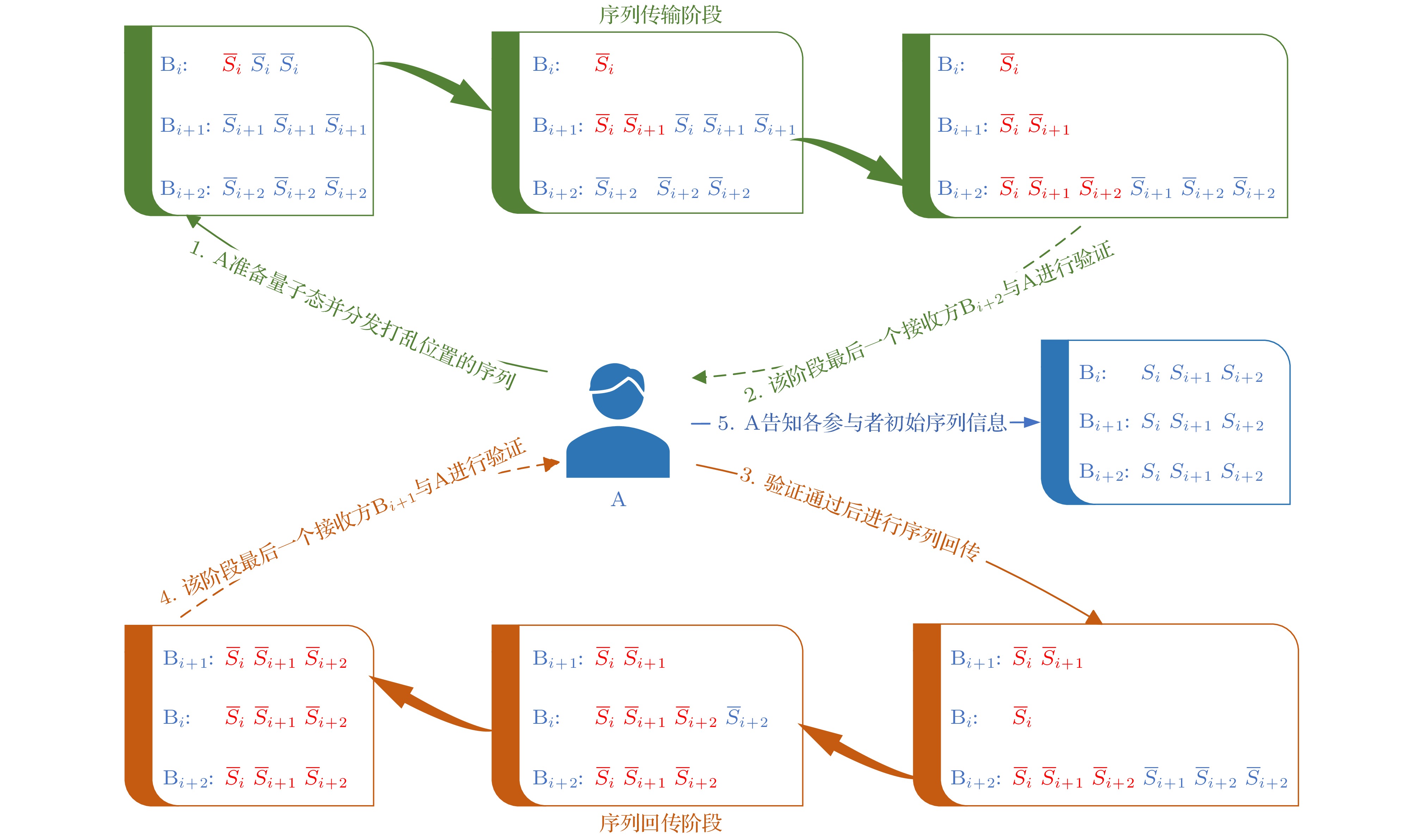
图 1 协议整体流程图. 其中红色标注的量子序列是在传输阶段参与者进行保留的序列, 蓝色标注的量子序列是在传输阶段不同参与者的传输回合中待发送的序列
Figure 1. The overall flowchart of the protocol. The quantum sequences marked in red are the sequences that the participants retain during the transmission stage, and the quantum sequences marked in blue are the sequences to be sent in the transmission rounds of different participants during the transmission phase.
图 2 有接收方退出时的协议流程, 其中红色标注的量子序列是在传输阶段参与者进行保留的序列, 蓝色标注的量子序列是在传输阶段不同参与者的传输回合中待发送的序列
Figure 2. The protocol flow when a receiver withdraws, the quantum sequences marked in red are the sequences that the participants retain during the transmission stage, and the quantum sequences marked in blue are the sequences to be sent in the transmission rounds of different participants during the transmission phase.
图 3 有新的接收方加入时的协议流程, 其中红色标注的量子序列是在传输阶段参与者进行保留的序列, 蓝色标注的量子序列是在传输阶段不同参与者的传输回合中待发送的序列
Figure 3. The protocol flow when a new receiver joins, the quantum sequences marked in red are the sequences that the participants retain during the transmission stage, and the quantum sequences marked in blue are the sequences to be sent in the transmission rounds of different participants during the transmission phase.
协议 [25] [26] [27] [28] [29] 提出的协议 量子态 广义GHZ态 Bell态 GHZ态 Bell态 Bell态 正交乘积态 参与者测量 单粒子测量 单粒子测量 单粒子测量 Bell态测量 Bell态/单粒子测量 单粒子测量 量子比特数(QR) $N(n - 1)$ $2 n-2$ $N(n+1)$ $2 nm$ $2 N(n - 1)$ $Nn$ 量子效率 $ \dfrac{1}{n - 1} $ $ \dfrac{1}{2 n - 2} $ $ \dfrac{1}{n + 1} $ $ \dfrac{1}{2 n} $ $ \dfrac{1}{2 n - 2} $ $\dfrac{\lfloor\log_2 n\rfloor + 1}{n}$ 窃听检测资源 诱饵粒子 诱饵粒子 GHZ 诱饵粒子 诱饵粒子 诱饵粒子 准备量子位以添加代理 单光子 Bell态 d级GHZ态 Bell态 Bell态 随机量子态序列 易受合谋攻击 No No No No No No 是否对粒子执行变换操作 No Yes Yes Yes No Yes -
[1] Hellman M, Diffie W 1976 IEEE Trans. Inf. Theory 22 644
 Google Scholar
Google Scholar
[2] Fujisaki E, Okamoto T 1999 Annual international cryptology conference Santa Barbara, California, USA, August 15–19, 1999 p537
[3] Bellare M, Desai A, Jokipii E, Rogaway P 1997 Proceedings 38 th Annual Symposium on Foundations of Computer Science Miami Beach, FL, USA, October 20–22, 1997 p394
[4] Feistel H 1973 Sci. Amer. 228 15
[5] Shor P W 1999 SIAM Rev. 41 303
 Google Scholar
Google Scholar
[6] Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing Philadelphia, Pennsylvania, May 22–24, 1996 p212
[7] Bennett C H, Brassard G 1984 Proc. Workshop on the Theory and Application of Cryptographic Techniques Santa Barbara, California, USA, August 19–22, 1984 p475
[8] 冯发勇, 张强 2007 物理学报 4 1924
 Google Scholar
Google Scholar
Feng F Y, Zhang Q 2007 Acta Phys. Sin. 4 1924
 Google Scholar
Google Scholar
[9] Zhao Z, Chen Y A, Zhang A N, Yang T, Briegel H J, Pan J W 2004 Nature 430 54
 Google Scholar
Google Scholar
[10] Wang T Y, Wen Q Y 2011 Chin. Phys. B 20 040307
 Google Scholar
Google Scholar
[11] Jiang S X, Zhao B, Liang X Z 2021 Chin. Phys. B 30 060303
 Google Scholar
Google Scholar
[12] Deng F G, Long G L, Liu X S 2003 Phys. Rev. A 68 042317
 Google Scholar
Google Scholar
[13] 赵宁, 江英华, 周贤韬 2022 物理学报 71 150304
 Google Scholar
Google Scholar
Zhao N, Jiang Y H, Zhou X T 2022 Acta Phys. Sin. 71 150304
 Google Scholar
Google Scholar
[14] Deng F G, Zhou H Y, Long G L 2006 J. Phys. A: Math. Gen. 39 14089
 Google Scholar
Google Scholar
[15] 孙莹, 杜建忠, 秦素娟, 温巧燕, 朱甫臣 2008 物理学报 08 4689
 Google Scholar
Google Scholar
Sun Y, Du J Z, Qin S J, Wen Q Y, Zhu F C 2008 Acta Phys. Sin. 08 4689
 Google Scholar
Google Scholar
[16] Dai Y W, Qin H Y 2015 Chin. Phys. Lett. 32 100301
 Google Scholar
Google Scholar
[17] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
 Google Scholar
Google Scholar
[18] Karlsson A, Koashi M, Imoto N 1999 Phys. Rev. A 59 162
 Google Scholar
Google Scholar
[19] Xiao L, Lu Long G, Deng F G, Pan J W 2004 Phys. Rev. A 69 052307
 Google Scholar
Google Scholar
[20] Yang Y, Wen Q, Zhu F 2007 Sci. China Ser. G-Phys. Mech. Astron. 50 331
 Google Scholar
Google Scholar
[21] Wang T Y, Wen Q Y, Chen X B, Guo F Z, Zhu F C 2008 Opt. Commun. 281 6130
 Google Scholar
Google Scholar
[22] Wang C, Zhang Y 2009 Chin. Phys. B 18 3238
 Google Scholar
Google Scholar
[23] Jia H Y, Wen Q Y, Gao F, Qin S J, Guo F Z 2012 Phys. Lett. A 376 1035
 Google Scholar
Google Scholar
[24] Hsu J L, Chong S K, Hwang T, Tsai C W 2013 Quantum Inf. Process. 12 331
 Google Scholar
Google Scholar
[25] Du Y T, Bao W S 2018 Chin. Phys. B 27 080304
 Google Scholar
Google Scholar
[26] Yang C W, Tsai C W 2020 Quantum Inf. Process. 19 1
 Google Scholar
Google Scholar
[27] Hu W, Zhou R G, Li X, Fan P, Tan C 2021 Quantum Inf. Process. 20 1
 Google Scholar
Google Scholar
[28] Tian Y, Wang J, Bian G, Chang J, Li J 2024 Adv. Quantum Technol. 7 2400116
 Google Scholar
Google Scholar
[29] Lin J, Chen C C, Huang C Y 2024 Physica A 638 129615
 Google Scholar
Google Scholar
[30] Yu S, Oh C H 2015 arXiv: 1502.01274 [quant-ph]
[31] Guo G P, Li C F, Shi B S, Li J, Guo G C 2001 Phys. Rev. A 64 042301
 Google Scholar
Google Scholar
[32] Jiang D H, Wang J, Liang X Q, Xu G B, Qi H F 2020 Int. J. Theor. Phys. 59 436
 Google Scholar
Google Scholar
[33] Jiang D H, Hu Q Z, Liang X Q, Xu G B 2020 Int. J. Theor. Phys. 59 1442
 Google Scholar
Google Scholar
[34] Walgate J, Hardy L 2002 Phys. Rev. Lett. 89 147901
 Google Scholar
Google Scholar
[35] Xu G B, Wen Q Y, Qin S J, Yang Y H, Gao F 2016 Phys. Rev. A 93 032341
 Google Scholar
Google Scholar
[36] Feng Y, Shi Y 2009 IEEE Trans. Inf. Theory 55 2799
 Google Scholar
Google Scholar
[37] Deng F G, Li X H, Zhou H Y, Zhang Z J 2005 Phys. Rev. A 72 044302
 Google Scholar
Google Scholar
[38] Li X H, Deng F G, Zhou H Y 2006 Phys. Rev. A 74 054302
 Google Scholar
Google Scholar
[39] Cabello A 2000 Phys. Rev. Lett. 85 5635
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 2022
- PDF Downloads: 30
- Cited By: 0















 DownLoad:
DownLoad: