-
在超冷费米系统中实现人造规范势的突破, 吸引了许多新问题的研究, 展现了许多新奇的物理现象. 本文研究了在环阱中, 具有自旋轨道耦合和塞曼作用的两体相互作用费米模型. 通过平面波展开的方法, 解析求解了两体费米系统的本征能态. 系统的总动量为守恒量, 可以在不同总动量空间中研究能谱. 研究发现: 随着塞曼相互作用增大, 在不同总动量空间, 两体费米系统的本征能量均逐渐降低, 系统基态从总动量为零空间转变到有限值空间. 从吸引到排斥相互作用, 无塞曼相互作用时, 基态总动量始终为零, 有塞曼相互作用时, 基态总动量从零转变为有限值. 通过单粒子和基态动量分布研究, 本文直观地揭示了由塞曼能级劈裂引起的基态转变.Experimental realization of artificial gauge field has made it possible to simulate important models with electromagnetic field or spin-orbit interaction in condensed matter physics, which opens a new avenue to engineer novel quantum states and phenomena. The spin-orbit coupled system reveals many significant phenomena in condensed matter physics, such as quantum spin Hall effect, topological insulator and topological superconductor. The combined effect of Zeeman interaction and spin-orbit coupling leads to a nontrivial topological phase. The analytic solution of few-body system provides an in-depth insight into the physical phenomena, which has been studied extensively. Through the analytic study of two-body physics, we show new quantum phenomena for various gauge field parameters. We investigate the two-body interacting fermionic gas with spin-orbit coupling and Zeeman interaction in a ring trap. Through the plane wave expansion method, two-body fermionic system is solved analytically. In the absence of Zeeman interaction, the total momentum of the ground state is zero. With the increase of Zeeman interaction, an energy level crossing occurs between the lowest energy levels for different total momentum spaces and the ground state changes from zero total momentum space to non-zero total momentum space. Considering the Zeeman interaction, the total momentum of the ground state changes from zero to finite value. The single particle analysis shows that the ground energy level transition is induced by Zeeman energy level splitting. The momentum distributions of the ground state are given to provide an intuitive physical picture. This work can be further extended to the exploration of the heteroatom system, lattice system and higher spin system.
-
Keywords:
- two-body Fermionic system /
- spin-orbit coupling /
- Zeeman interaction
[1] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] 施婷婷, 汪六九, 王璟琨, 张威 2020 物理学报 69 016701
Google Scholar
Shi T T, Wang L J, Wang J K, Zhang W 2020 Acta Phys. Sin. 69 016701
Google Scholar
[4] Lin Y J, Garcis K J, Spielman I B 2011 Nature 83 471
[5] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[6] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[7] Huang L H, Meng Z M, Wang P J, Peng P, Zhang S L, Chen L C, Li D H, Zhou Q, Zhang J 2016 Nat. Phys. 12 540
Google Scholar
[8] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y, Chen S, Liu X J, Pan J W 2016 Sicence 354 83
Google Scholar
[9] Zhou J, Zhang W, Yi W 2011 Phys. Rev. A 84 063603
Google Scholar
[10] Chen J, Hu H, Gao X L 2014 Phys. Rev. A 90 023619
Google Scholar
[11] Meng Z, Huang L, Peng P, Li D, Chen L, Xu Y, Zhang C, Wang P, Zhang J 2016 Phys. Rev. Lett. 117 235304
Google Scholar
[12] Dong L, Jiang L, Pu H 2013 New J. Phys. 15 075014
Google Scholar
[13] Chen C 2013 Phys. Rev. Lett. 111 235302
Google Scholar
[14] Qu C L, Zheng Z, Gong M, Xu Y, Mao L, Zou X B, Guo G C, Zhang C W 2013 Nat. Commun. 4 2710
Google Scholar
[15] Zhang W, Yi W 2013 Nat. Commun. 4 2711
Google Scholar
[16] Valdés-Curiel A, Trypogeorgos D, Liang Q Y, Anderson R P, Spielman I B arXiv: 1907.08637
[17] Liu X J, Hu H, Pu H 2015 Chin. Phys. B 24 050502
Google Scholar
[18] Cao Y, Liu X J, He L Y, Long G L, Hu H 2015 Phys. Rev. A 91 023609
Google Scholar
[19] Devreese J P A, Tempere J, Sá de Melo C A R 2014 Phys. Rev. Lett. 113 165304
Google Scholar
[20] Luo X B, Zhou K Z, Liu W M, Liang Z X, Zhang Z D 2014 Phys. Rev. A 89 043612
Google Scholar
[21] Xu Y, Zhang C W 2015 Phys. Rev. Lett. 114 110401
Google Scholar
[22] Zhou K Z, Zhang Z D 2019 J. Phys. Chem. Solids 128 207
Google Scholar
[23] Yang S, Wu F, Yi W, Zhang P 2019 Phys. Rev. A 100 043601
Google Scholar
[24] Yu Z Q, Zhai H 2011 Phys. Rev. Lett. 107 195305
Google Scholar
[25] Vyasanakere J P, Shenoy V B 2012 New J. Phys. 14 043041
Google Scholar
[26] Usui A, Fogarty T, Campbell S, Gardiner S A, Busch T 2020 New J. Phys. 22 013050
Google Scholar
[27] Li Q M, Callaway J 1991 Phys. Rev. B 43 3278
Google Scholar
[28] Cui X L, Yi W 2014 Phys. Rev. X 4 031026
[29] Wang J K, Yi W, Zhang W 2016 Front. Phys. 11 118102
Google Scholar
[30] Peng S G, Zhang C X, Tan S, Jiang K J 2018 Phys. Rev. Lett. 120 060408
Google Scholar
[31] Cui X L 2017 Phys. Rev. A 95 030701
Google Scholar
[32] Gong B H, Li S, Zhang X H 2019 Phys. Rev. A 99 012703
Google Scholar
[33] Chen X, Guan L M, Chen S 2011 Eur. Phys. J. D 64 459
Google Scholar
[34] Song B, He C D, Zhang S C, Hajiyev E, Huang W, Liu X J, Jo G B 2016 Phys. Rev. A 94 061604
Google Scholar
[35] Olshanii M 1998 Phys. Rev. Lett. 81 938
Google Scholar
[36] Busch T, Englert B G, Rzazewski K, Wilkens M 2001 J. Phys. B 34 4571
Google Scholar
[37] Chen X, Hu H P, Jiang Y Z, Chen S 2013 Eur. Phys. J. D 67 166
Google Scholar
-
图 1 最低能量
$ {E_{\rm{0}}}$ 随着自旋轨道耦合参量$ \alpha$ 的变化. 插图为$ {E_0} + {\alpha ^2}$ 随$ \alpha$ 的变化,$ n = 0$ ,$ g = 1$ ,$ \beta = 0$ Fig. 1. The lowest energy
${E_{\rm{0}}}$ versus spin-orbit coupling parameter$\alpha $ . Insert is${E_0} + {\alpha ^2}$ versus$\alpha $ .$n = 0$ ,$g = 1$ ,$\beta = 0$ .
图 2 在弱相互作用条件下最低能量
$ {E_{\rm{0}}}$ 和$ {E_1}$ 随塞曼系数$ \beta $ 的变化,$ g = 1$ ,$ \alpha = 1.2{\text{π}}$ Fig. 2. The lowest energies
${E_{\rm{0}}}$ and${E_1}$ versus Zeeman interaction parameter$\beta $ in the weak interaction condition.$g = 1$ ,$\alpha = 1.2{\text{π}}$ .
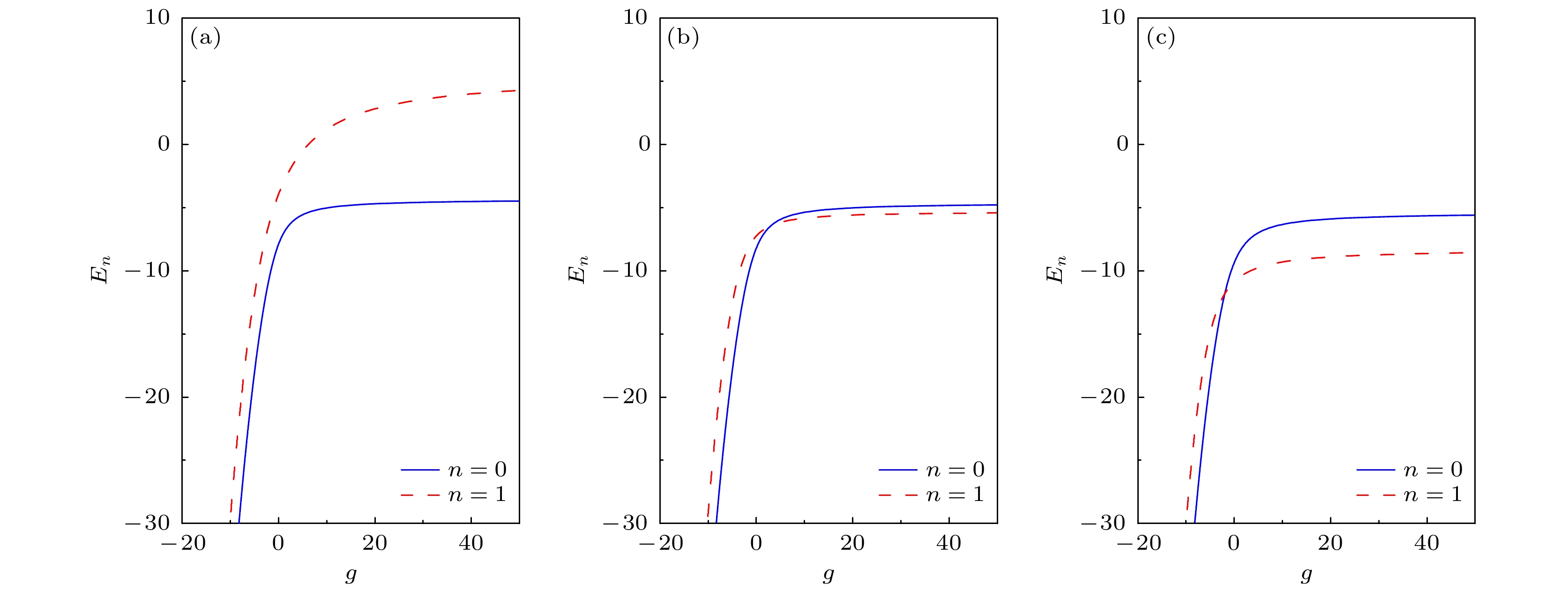
图 3 能量
${E_0}$ 和${E_1}$ 随着接触相互作用g的变化,$\alpha = 1.2{\text{π}}$ (a)$\beta = 0$ ; (b)$\beta = {\text{π}}$ ; (c)$\beta = 2{\text{π}}$ Fig. 3. The energies
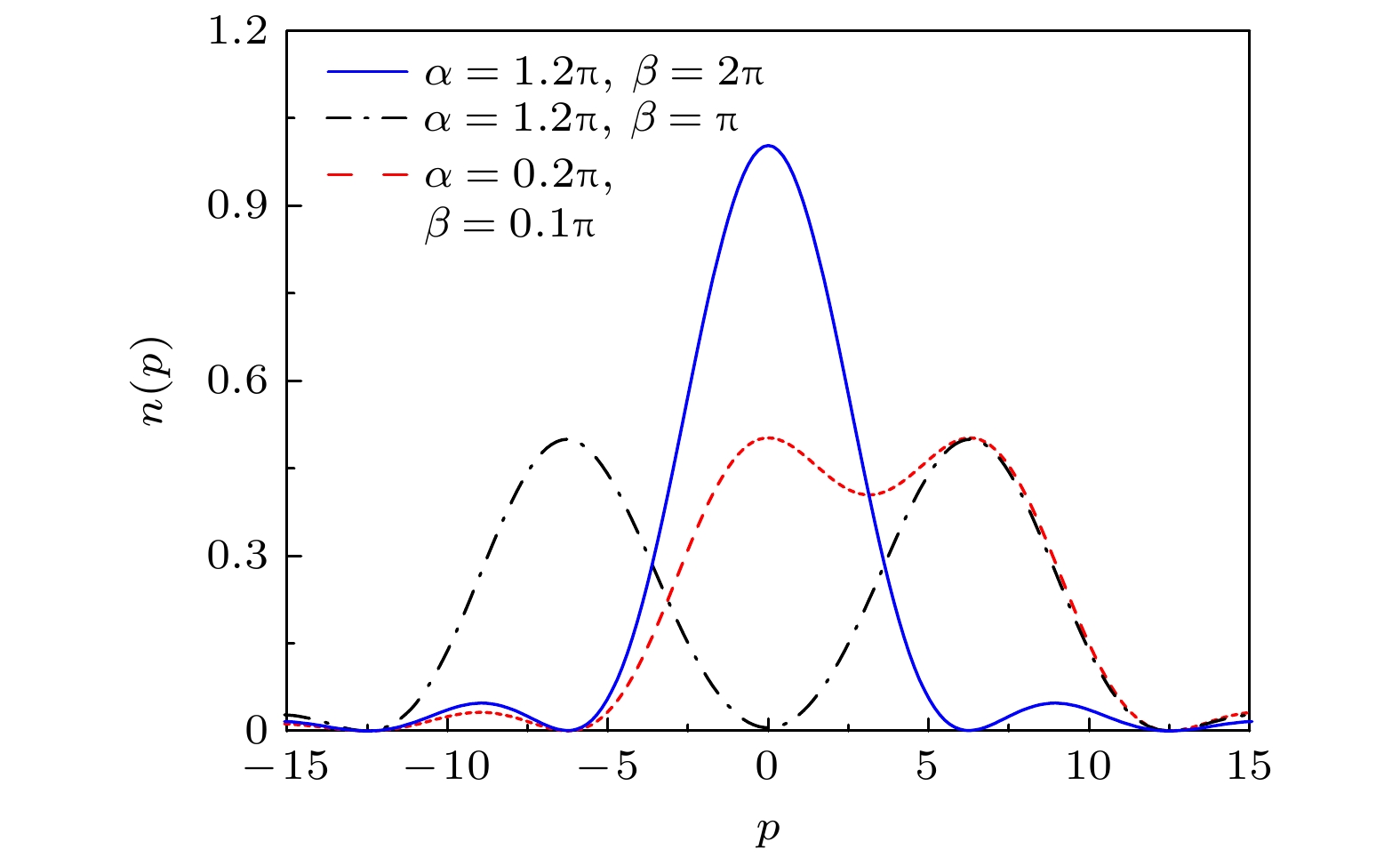
${E_{\rm{0}}}$ and${E_1}$ versus contact interaction parameter g,$\alpha = 1.2{\text{π}}$ : (a)$\beta = 0$ ; (b)$\beta = {\text{π}}$ ; (c)$\beta = 2{\text{π}}$ .
图 4 单粒子能级e–和e+ (a)
$ \alpha = 0.2{\text{π}}$ ,$ \beta = 0.1{\text{π}}$ ; (b)$ \alpha = 1.2{\text{π}}$ ,$ \beta = {\text{π}}$ ; (c)$ \alpha = 1.2{\text{π}}$ ,$ \beta = 2{\text{π}}$ Fig. 4. The single particle eigenenergies with two branches e– and e+: (a)
$\alpha = 0.2{\text{π}}$ ,$\beta = 0.1{\text{π}}$ ; (b)$\alpha = 1.2{\text{π}}$ ,$\beta = {\text{π}}$ ; (c)$\alpha = 1.2{\text{π}}$ ,$\beta = 2{\text{π}}$ . -
[1] Zhai H 2015 Rep. Prog. Phys. 78 026001
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] 施婷婷, 汪六九, 王璟琨, 张威 2020 物理学报 69 016701
Google Scholar
Shi T T, Wang L J, Wang J K, Zhang W 2020 Acta Phys. Sin. 69 016701
Google Scholar
[4] Lin Y J, Garcis K J, Spielman I B 2011 Nature 83 471
[5] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[6] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[7] Huang L H, Meng Z M, Wang P J, Peng P, Zhang S L, Chen L C, Li D H, Zhou Q, Zhang J 2016 Nat. Phys. 12 540
Google Scholar
[8] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y, Chen S, Liu X J, Pan J W 2016 Sicence 354 83
Google Scholar
[9] Zhou J, Zhang W, Yi W 2011 Phys. Rev. A 84 063603
Google Scholar
[10] Chen J, Hu H, Gao X L 2014 Phys. Rev. A 90 023619
Google Scholar
[11] Meng Z, Huang L, Peng P, Li D, Chen L, Xu Y, Zhang C, Wang P, Zhang J 2016 Phys. Rev. Lett. 117 235304
Google Scholar
[12] Dong L, Jiang L, Pu H 2013 New J. Phys. 15 075014
Google Scholar
[13] Chen C 2013 Phys. Rev. Lett. 111 235302
Google Scholar
[14] Qu C L, Zheng Z, Gong M, Xu Y, Mao L, Zou X B, Guo G C, Zhang C W 2013 Nat. Commun. 4 2710
Google Scholar
[15] Zhang W, Yi W 2013 Nat. Commun. 4 2711
Google Scholar
[16] Valdés-Curiel A, Trypogeorgos D, Liang Q Y, Anderson R P, Spielman I B arXiv: 1907.08637
[17] Liu X J, Hu H, Pu H 2015 Chin. Phys. B 24 050502
Google Scholar
[18] Cao Y, Liu X J, He L Y, Long G L, Hu H 2015 Phys. Rev. A 91 023609
Google Scholar
[19] Devreese J P A, Tempere J, Sá de Melo C A R 2014 Phys. Rev. Lett. 113 165304
Google Scholar
[20] Luo X B, Zhou K Z, Liu W M, Liang Z X, Zhang Z D 2014 Phys. Rev. A 89 043612
Google Scholar
[21] Xu Y, Zhang C W 2015 Phys. Rev. Lett. 114 110401
Google Scholar
[22] Zhou K Z, Zhang Z D 2019 J. Phys. Chem. Solids 128 207
Google Scholar
[23] Yang S, Wu F, Yi W, Zhang P 2019 Phys. Rev. A 100 043601
Google Scholar
[24] Yu Z Q, Zhai H 2011 Phys. Rev. Lett. 107 195305
Google Scholar
[25] Vyasanakere J P, Shenoy V B 2012 New J. Phys. 14 043041
Google Scholar
[26] Usui A, Fogarty T, Campbell S, Gardiner S A, Busch T 2020 New J. Phys. 22 013050
Google Scholar
[27] Li Q M, Callaway J 1991 Phys. Rev. B 43 3278
Google Scholar
[28] Cui X L, Yi W 2014 Phys. Rev. X 4 031026
[29] Wang J K, Yi W, Zhang W 2016 Front. Phys. 11 118102
Google Scholar
[30] Peng S G, Zhang C X, Tan S, Jiang K J 2018 Phys. Rev. Lett. 120 060408
Google Scholar
[31] Cui X L 2017 Phys. Rev. A 95 030701
Google Scholar
[32] Gong B H, Li S, Zhang X H 2019 Phys. Rev. A 99 012703
Google Scholar
[33] Chen X, Guan L M, Chen S 2011 Eur. Phys. J. D 64 459
Google Scholar
[34] Song B, He C D, Zhang S C, Hajiyev E, Huang W, Liu X J, Jo G B 2016 Phys. Rev. A 94 061604
Google Scholar
[35] Olshanii M 1998 Phys. Rev. Lett. 81 938
Google Scholar
[36] Busch T, Englert B G, Rzazewski K, Wilkens M 2001 J. Phys. B 34 4571
Google Scholar
[37] Chen X, Hu H P, Jiang Y Z, Chen S 2013 Eur. Phys. J. D 67 166
Google Scholar
-
[1] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维 ${\cal {PT}}$ 对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. 物理学报, 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796[2] 王志梅, 王虹, 薛乃涛, 成高艳. 自旋轨道耦合量子点系统中的量子相干. 物理学报, 2022, 71(7): 078502. doi: 10.7498/aps.71.20212111 [3] 张爱霞, 姜艳芳, 薛具奎. 光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱特性. 物理学报, 2021, 70(20): 200302. doi: 10.7498/aps.70.20210705 [4] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽. 自旋轨道耦合Su-Schrieffer-Heeger原子链系统的电子输运特性. 物理学报, 2021, 70(8): 087301. doi: 10.7498/aps.70.20201742 [5] 施婷婷, 汪六九, 王璟琨, 张威. 自旋轨道耦合量子气体中的一些新进展. 物理学报, 2020, 69(1): 016701. doi: 10.7498/aps.69.20191241 [6] 李志强, 王月明. 一维谐振子束缚的自旋轨道耦合玻色气体. 物理学报, 2019, 68(17): 173201. doi: 10.7498/aps.68.20190143 [7] 梁滔, 李铭. 自旋轨道耦合系统中的整数量子霍尔效应. 物理学报, 2019, 68(11): 117101. doi: 10.7498/aps.68.20190037 [8] 杨圆, 陈帅, 李小兵. Rashba自旋轨道耦合下square-octagon晶格的拓扑相变. 物理学报, 2018, 67(23): 237101. doi: 10.7498/aps.67.20180624 [9] 孟增明, 黄良辉, 彭鹏, 陈良超, 樊浩, 王鹏军, 张靖. 光学相位锁定激光在原子玻色-爱因斯坦凝聚中实现拉曼耦合. 物理学报, 2015, 64(24): 243202. doi: 10.7498/aps.64.243202 [10] 刘胜利, 厉建峥, 程杰, 王海云, 李永涛, 张红光, 李兴鳌. 强自旋轨道耦合化合物Sr2-xLaxIrO4的掺杂和拉曼谱学. 物理学报, 2015, 64(20): 207103. doi: 10.7498/aps.64.207103 [11] 陈东海, 杨谋, 段后建, 王瑞强. 自旋轨道耦合作用下石墨烯pn结的电子输运性质. 物理学报, 2015, 64(9): 097201. doi: 10.7498/aps.64.097201 [12] 陈光平. 简谐+四次势中自旋轨道耦合旋转玻色-爱因斯坦凝聚体的基态结构. 物理学报, 2015, 64(3): 030302. doi: 10.7498/aps.64.030302 [13] 龚士静, 段纯刚. 金属表面Rashba自旋轨道耦合作用研究进展. 物理学报, 2015, 64(18): 187103. doi: 10.7498/aps.64.187103 [14] 陈艳丽, 彭向阳, 杨红, 常胜利, 张凯旺, 钟建新. 拓扑绝缘体Bi2Se3中层堆垛效应的第一性原理研究. 物理学报, 2014, 63(18): 187303. doi: 10.7498/aps.63.187303 [15] 李桂霞, 姜永超, 凌翠翠, 马红章, 李鹏. HF+离子在旋轨耦合作用下电子态的特性. 物理学报, 2014, 63(12): 127102. doi: 10.7498/aps.63.127102 [16] 张磊, 李辉武, 胡梁宾. 二维自旋轨道耦合电子气中持续自旋螺旋态的稳定性的研究. 物理学报, 2012, 61(17): 177203. doi: 10.7498/aps.61.177203 [17] 杨杰, 董全力, 江兆潭, 张杰. 自旋轨道耦合作用对碳纳米管电子能带结构的影响. 物理学报, 2011, 60(7): 075202. doi: 10.7498/aps.60.075202 [18] 余志强, 谢泉, 肖清泉. 狭义相对论下电子自旋轨道耦合对X射线光谱的影响. 物理学报, 2010, 59(2): 925-931. doi: 10.7498/aps.59.925 [19] 肖贤波, 李小毛, 陈宇光. 含stubs量子波导系统的电子自旋极化输运性质. 物理学报, 2009, 58(11): 7909-7913. doi: 10.7498/aps.58.7909 [20] 周青春, 王嘉赋, 徐荣青. 自旋-轨道耦合对磁性绝缘体磁光Kerr效应的影响. 物理学报, 2002, 51(7): 1639-1644. doi: 10.7498/aps.51.1639
下载:
计量
- 文章访问数: 4951
- PDF下载量: 62
- 被引次数: 0
