-
Multi-physics coupling calculation has applications in many important research fields. If particle transport process is included in this calculation, Monte Carlo method is often used to simulate this process and usually a large amount of calculation time is needed. So, efficient Monte Carlo algorithm for time-dependent particle transport problem is important for an efficiently coupling calculation, which inevitably relies on large-scale parallel calculation. Based on the characteristic of time-dependent particle transport problem, two methods are proposed in this paper to achieve high- efficiency calculation. One is a tally-reducing algorithm which is used in the coupling of transport simulation and burnup calculation. By reducing the quantity of data which should be reduced necessarily, this method can reduce the calculation time largely. It can be seen that a new coupling mode for these two processes in MPI environment has a larger value when model scale is larger than the sample size. The other method is an adaptive method of setting the sample size of Monte Carlo simulation. The law of large number assures that the Monte Carlo method will obtain an exact solution when the sample scale tends to infinity. But generally, no one knows which sample scale is big enough for obtaining a solution with target precision in advance. So, the common strategy is to set a huge-enough sample scale by experience and conduct the posterior check for all results. Apparently, this way cannot be efficient because the calculation will go on after the precision of solution has reached an object value. Another popular method is to set the sample size to rely on the relative error of some single calculation. The sample size is enlarged without a break until the relative error is less than some presetting value. This method is not suitable either, because Monte Carlo particle transport simulation will gives feedbacks to other process which is composed of many tallies. It is inappropriate to adjust the sample size according to the relative error of any calculation. Relying on the generalization of the Shannon entropy concept and an on-the-fly diagnosis rule for a entropy value sequence, the adaptive method proposed in this paper can reduce the original huge sample scale to a reasonable level. By numerically testing some non-trivial examples, both algorithms can reduce the calculation time largely, with the results kept almost unchanged, so the efficiency is high in these cases.
[1] 杜书华, 张树发, 冯庭桂, 王元璋, 邢静茹 1989 输运问题的计算机模拟 (长沙: 湖南科技出版社) 第47页
Du S H, Zhang S F, Feng T G, Wang Y Z, Xing J R 1989 Computer Simulation of Transport Problems (Changsha: Hunan Science and Technology Press) p47 (in Chinese)
[2] Smith K, Forget B 2013 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering SunValley, Idaho, USA, May 5–9, 2013 p18
[3] Alme H J 2001 J. Supercomput. 18 5
Google Scholar
[4] 李刚, 雷伟, 张宝印, 邓力, 马彦, 李瑞 2014 核动力工程 S2 228
Google Scholar
Li G, Lei W, Zhang B Y, Deng L, Ma Y, Li R 2014 Nucl. Power Eng S2 228
Google Scholar
[5] Brown F B, Martin W R 2004 High Performance Computing and Monte Carlo (Los Alamos: Los Alamos National Lab.) Report No. LA-UR-04-4532
[6] Romano P, Forget B, Brown F 2011 Prog. Nucl. Sci. Technol. 2 670
Google Scholar
[7] Kelly D J, Sutton T M, Wilson S C 2012 Proceedings of PHYSOR 2012 Knoxville, Tennessee, USA, April 15–20, 2012 p1
[8] Kelly D J, Aviles B N, Herman B R 2013 Proceedings of M&C 2013 Sun Valley, Idaho, USA, May 5–9, 2013 p2962
[9] 上官丹骅, 邓力, 李刚, 张宝印, 马彦, 付元光, 李瑞, 胡小利 2016 物理学报 65 062801
Google Scholar
Shangguan D H, Deng L, Li G, Zhang B Y, Ma Y, Fu Y G, Li R, Hu X L 2016 Acta Phys. Sin. 65 062801
Google Scholar
[10] Shangguan D H, Li G, Zhang B Y, Deng L, Ma Y, Fu Y G, Li R, Hu X L 2016 Nucl. Sci. Eng. 182 555
Google Scholar
[11] Ueki T, Brown F B 2005 Nucl. Sci. Eng. 149 38
Google Scholar
[12] Natio Y, Yang J 2004 J. Nucl. Sci. Technol. 41 559
Google Scholar
[13] Ueki T 2008 Nucl. Sci. Eng. 160 242
Google Scholar
[14] 上官丹骅, 姬志成, 邓力, 李瑞, 李刚, 付元光 2019 物理学报 68 122801
Google Scholar
Shangguan D H, Ji Z C, Deng L, Li R, Li G, Fu Y G 2019 Acta Phys. Sin. 68 122801
Google Scholar
[15] 上官丹骅, 邓力, 李刚, 张宝印 2018 强激光与粒子束 30 016004
Google Scholar
Shangguan D H, Deng L, Li G, Zhang B Y 2018 High Power Laser and Particle Beams 30 016004
Google Scholar
-
图 1 新旧方法计数与燃耗计算时间之和的对比
Fig. 1. Comparison of the total time of tally reduce and burnup calculation by using old and new methods.
表 1 常见算法优缺点比较
Table 1. Relative merits of common algorithms.
相关算法 大规模动态和定态输运问题高效蒙特卡罗模拟难点 存不下 算不快 算不准 区域分解 √
每个进程存储分片网格×
通信增加时间、负载不平衡×
方差无法精确估计数据分解 √
输运与计数进程分离×
增加额外通信时间—
无影响样本并行 ×
区域复制, 增加内存√
减少单进程计算量—
无影响偏倚算法 ×
增加算法相关内存√
效率提高√
效率提高增加样本 ×
增加样本数相关内存×
计算量增加√
大数定律保证
下载: 导出CSV
表 2 对于一个包含141万非结构六面体网格的模型, 全过程计算结果与计算时间比较
Table 2. Comparison of the results and calculation time for the whole simulation for the model including 1.41 million unstructured hexahedral meshes.
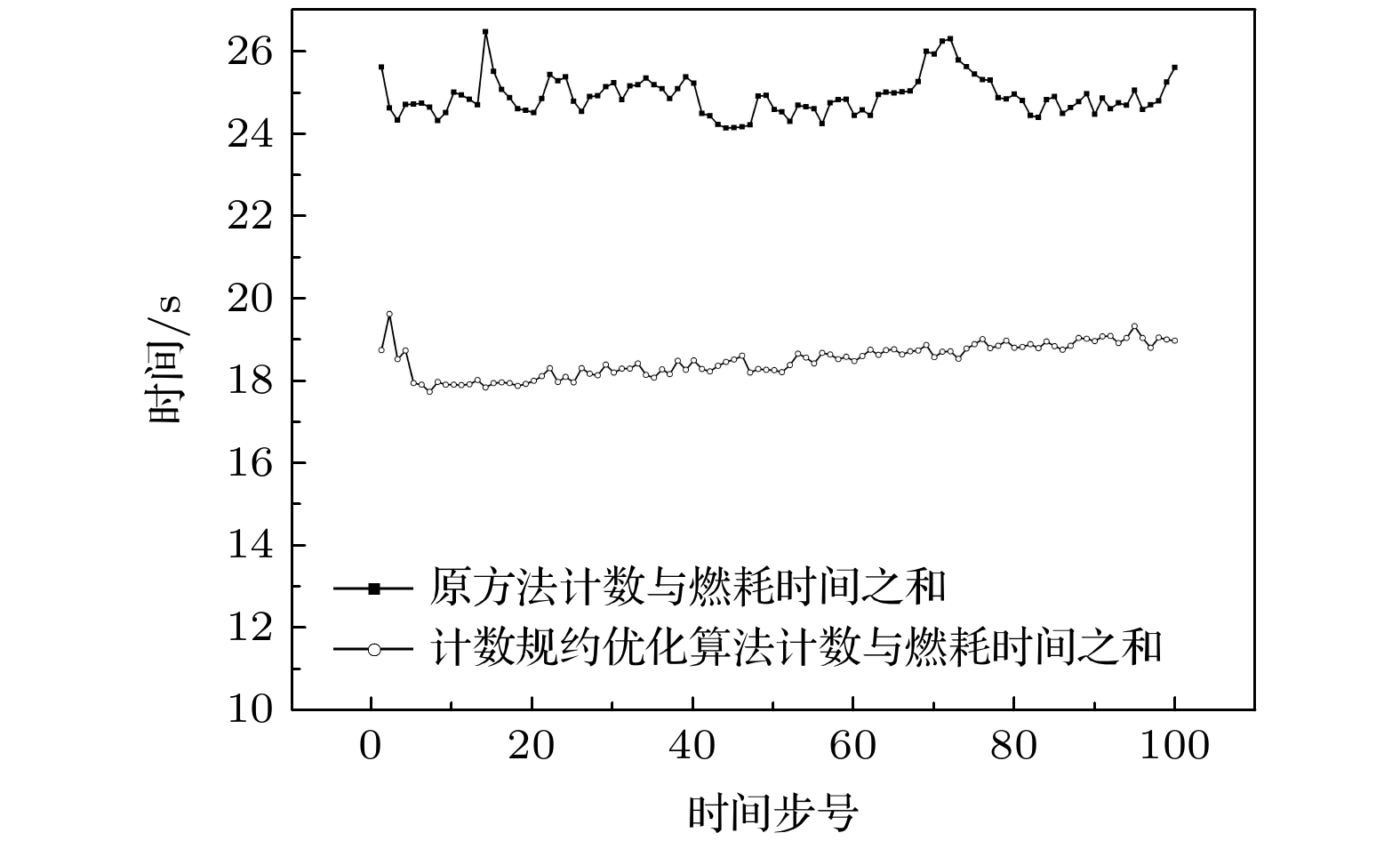
总释放能量 总计算时间/h 原程序 1.000 22.43 采用计数规约优化算法 1.009 18.98
下载: 导出CSV
表 3 对于一个包含550万非结构六面体网格的模型, 定态迭代计算结果与计算时间比较
Table 3. Comparison of the
$ \lambda $ and calculation time for the iteration calculation for the model including 5.50 million unstructured hexahedral meshes.$ \lambda $ 总计算时间/h 原程序 2.964 21.38 采用样本数自适应算法 2.979 9.09
下载: 导出CSV
表 4 对于一个包含2233万非结构六面体网格的模型, 全过程计算结果与计算时间比较
Table 4. Comparison of the results and calculation time for the whole simulation for the model including 22.33 million unstructured hexahedral meshes.
总释放能量 总计算时间 — d 原程序 1.000 9.63 采用样本数自适应算法 0.996 5.88
下载: 导出CSV
-
[1] 杜书华, 张树发, 冯庭桂, 王元璋, 邢静茹 1989 输运问题的计算机模拟 (长沙: 湖南科技出版社) 第47页
Du S H, Zhang S F, Feng T G, Wang Y Z, Xing J R 1989 Computer Simulation of Transport Problems (Changsha: Hunan Science and Technology Press) p47 (in Chinese)
[2] Smith K, Forget B 2013 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering SunValley, Idaho, USA, May 5–9, 2013 p18
[3] Alme H J 2001 J. Supercomput. 18 5
Google Scholar
[4] 李刚, 雷伟, 张宝印, 邓力, 马彦, 李瑞 2014 核动力工程 S2 228
Google Scholar
Li G, Lei W, Zhang B Y, Deng L, Ma Y, Li R 2014 Nucl. Power Eng S2 228
Google Scholar
[5] Brown F B, Martin W R 2004 High Performance Computing and Monte Carlo (Los Alamos: Los Alamos National Lab.) Report No. LA-UR-04-4532
[6] Romano P, Forget B, Brown F 2011 Prog. Nucl. Sci. Technol. 2 670
Google Scholar
[7] Kelly D J, Sutton T M, Wilson S C 2012 Proceedings of PHYSOR 2012 Knoxville, Tennessee, USA, April 15–20, 2012 p1
[8] Kelly D J, Aviles B N, Herman B R 2013 Proceedings of M&C 2013 Sun Valley, Idaho, USA, May 5–9, 2013 p2962
[9] 上官丹骅, 邓力, 李刚, 张宝印, 马彦, 付元光, 李瑞, 胡小利 2016 物理学报 65 062801
Google Scholar
Shangguan D H, Deng L, Li G, Zhang B Y, Ma Y, Fu Y G, Li R, Hu X L 2016 Acta Phys. Sin. 65 062801
Google Scholar
[10] Shangguan D H, Li G, Zhang B Y, Deng L, Ma Y, Fu Y G, Li R, Hu X L 2016 Nucl. Sci. Eng. 182 555
Google Scholar
[11] Ueki T, Brown F B 2005 Nucl. Sci. Eng. 149 38
Google Scholar
[12] Natio Y, Yang J 2004 J. Nucl. Sci. Technol. 41 559
Google Scholar
[13] Ueki T 2008 Nucl. Sci. Eng. 160 242
Google Scholar
[14] 上官丹骅, 姬志成, 邓力, 李瑞, 李刚, 付元光 2019 物理学报 68 122801
Google Scholar
Shangguan D H, Ji Z C, Deng L, Li R, Li G, Fu Y G 2019 Acta Phys. Sin. 68 122801
Google Scholar
[15] 上官丹骅, 邓力, 李刚, 张宝印 2018 强激光与粒子束 30 016004
Google Scholar
Shangguan D H, Deng L, Li G, Zhang B Y 2018 High Power Laser and Particle Beams 30 016004
Google Scholar
下载:
计量
- 文章访问数: 4578
- PDF下载量: 93
- 被引次数: 0
