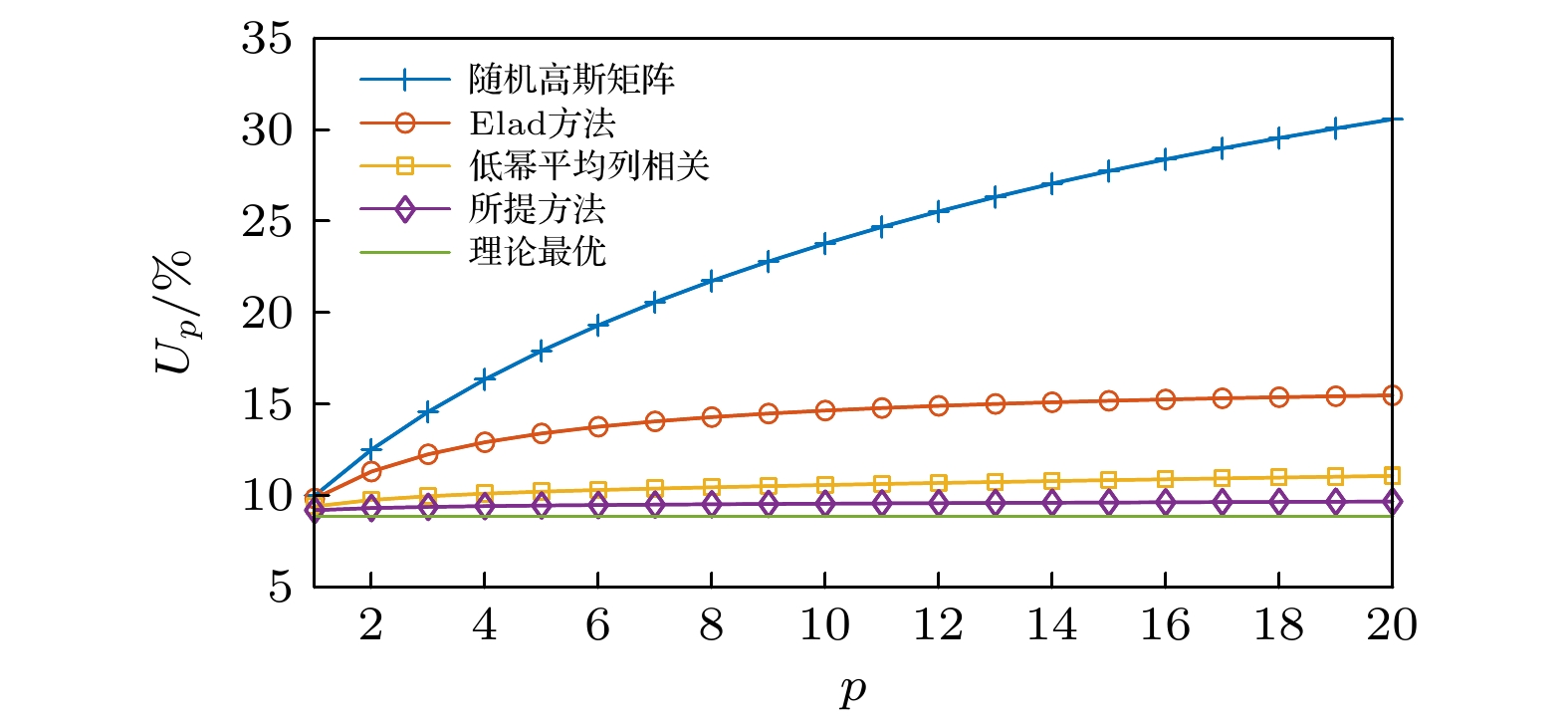
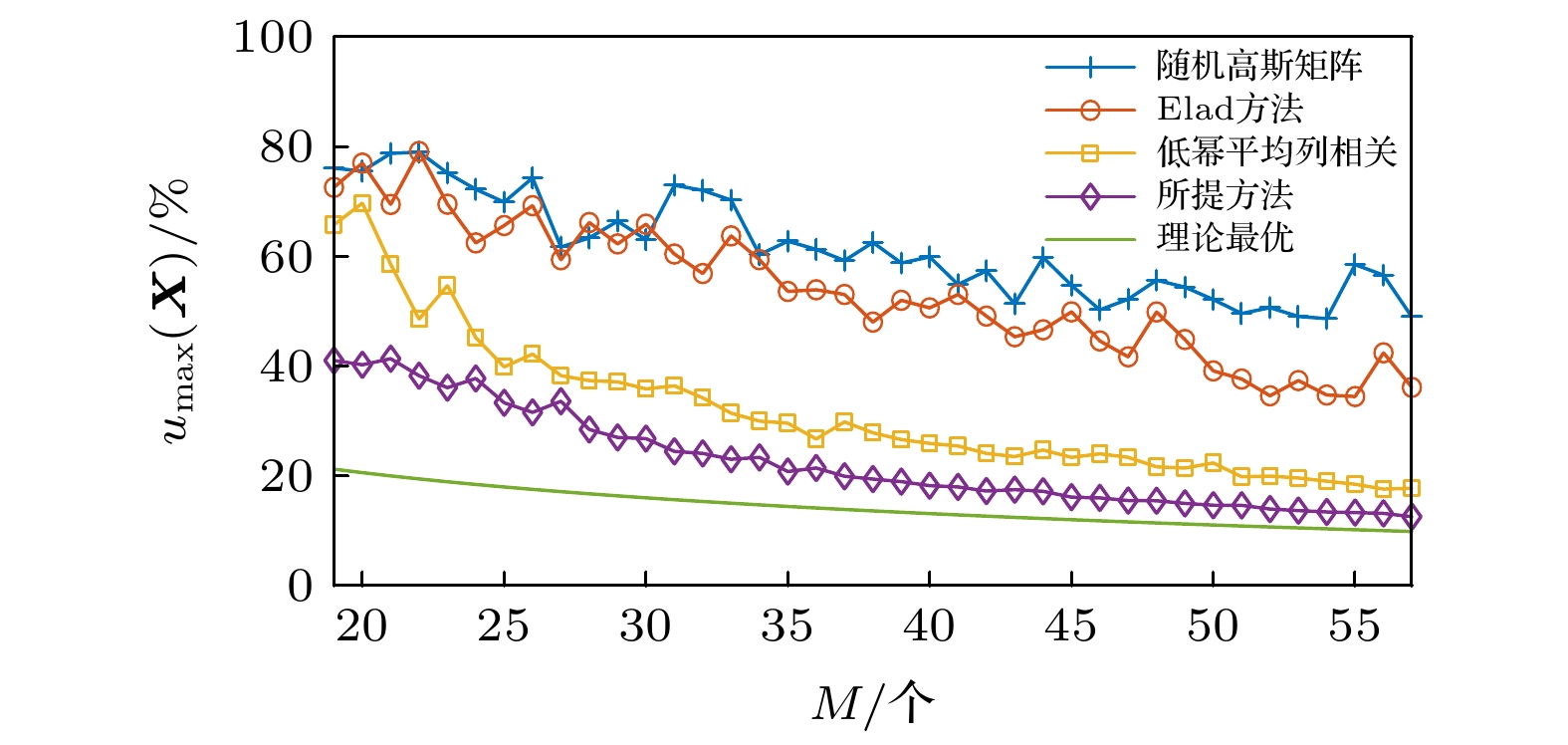
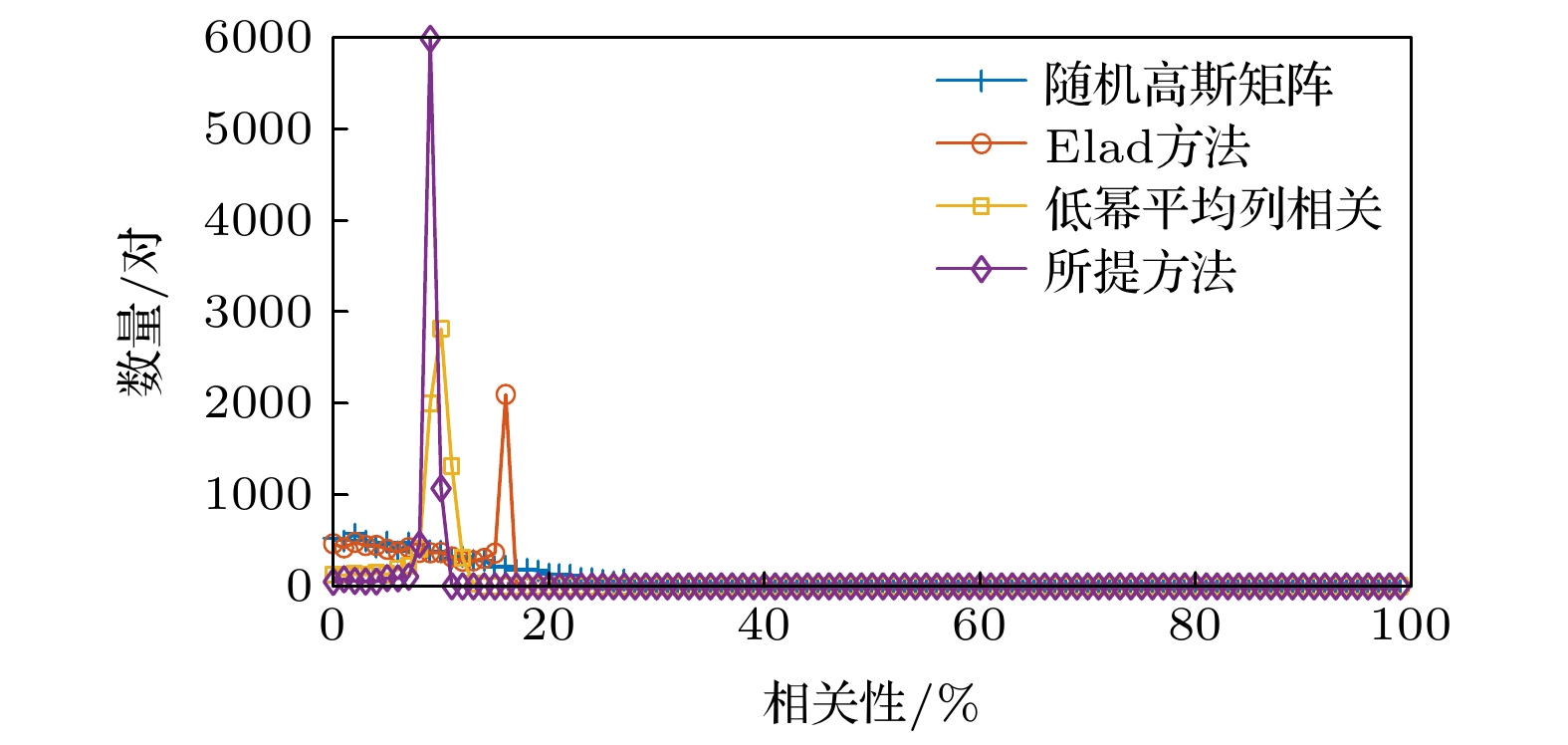
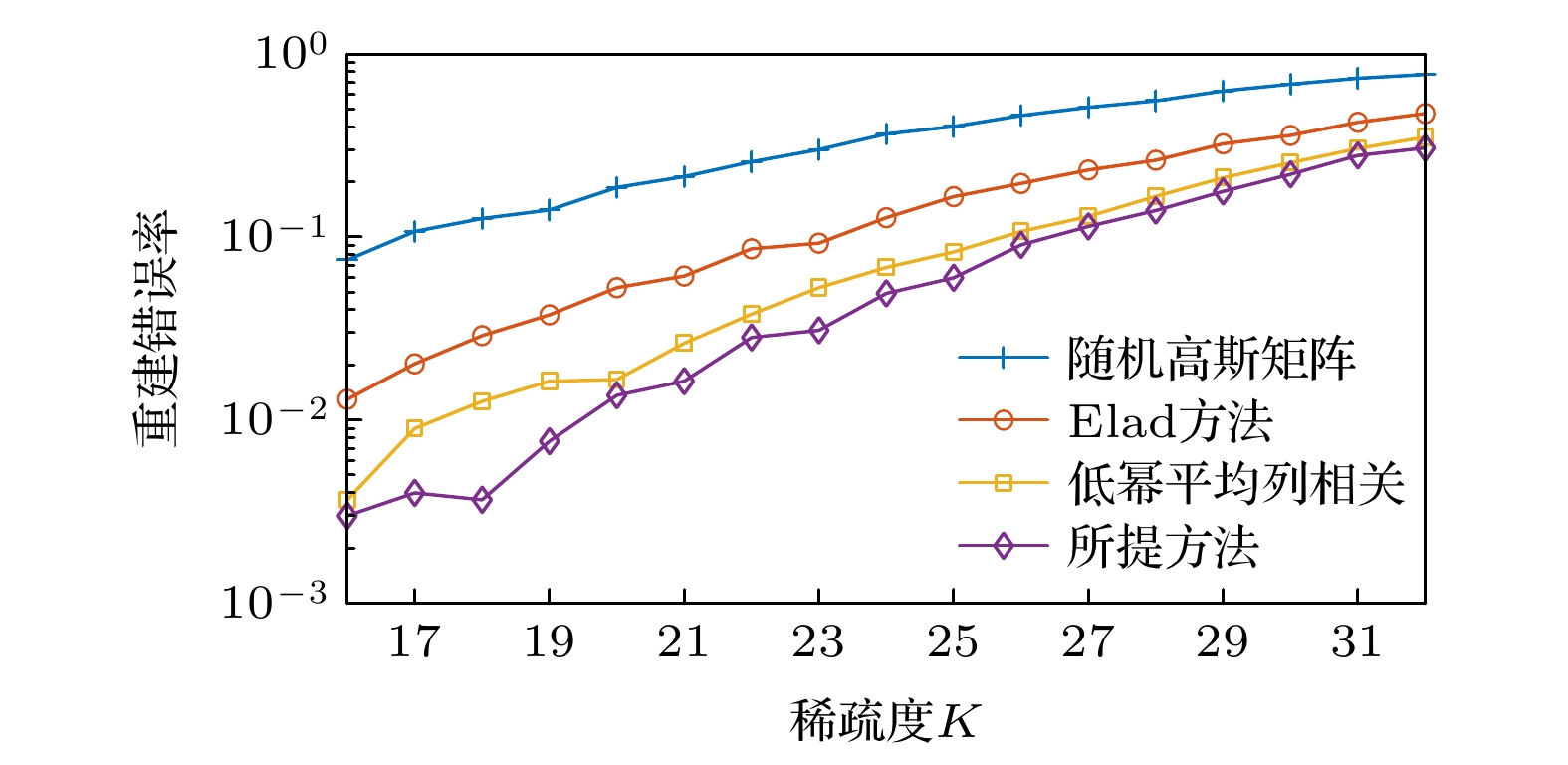
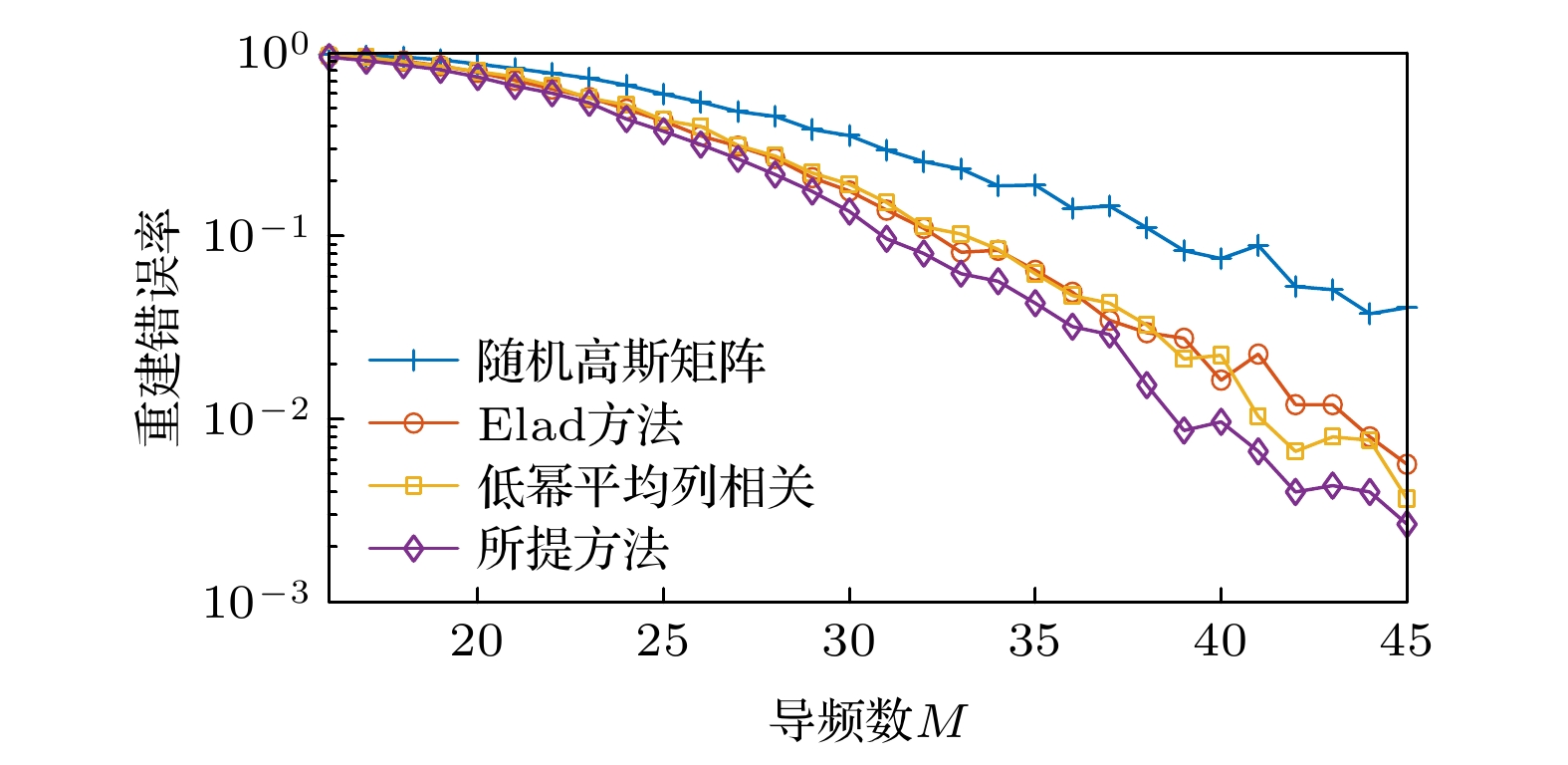
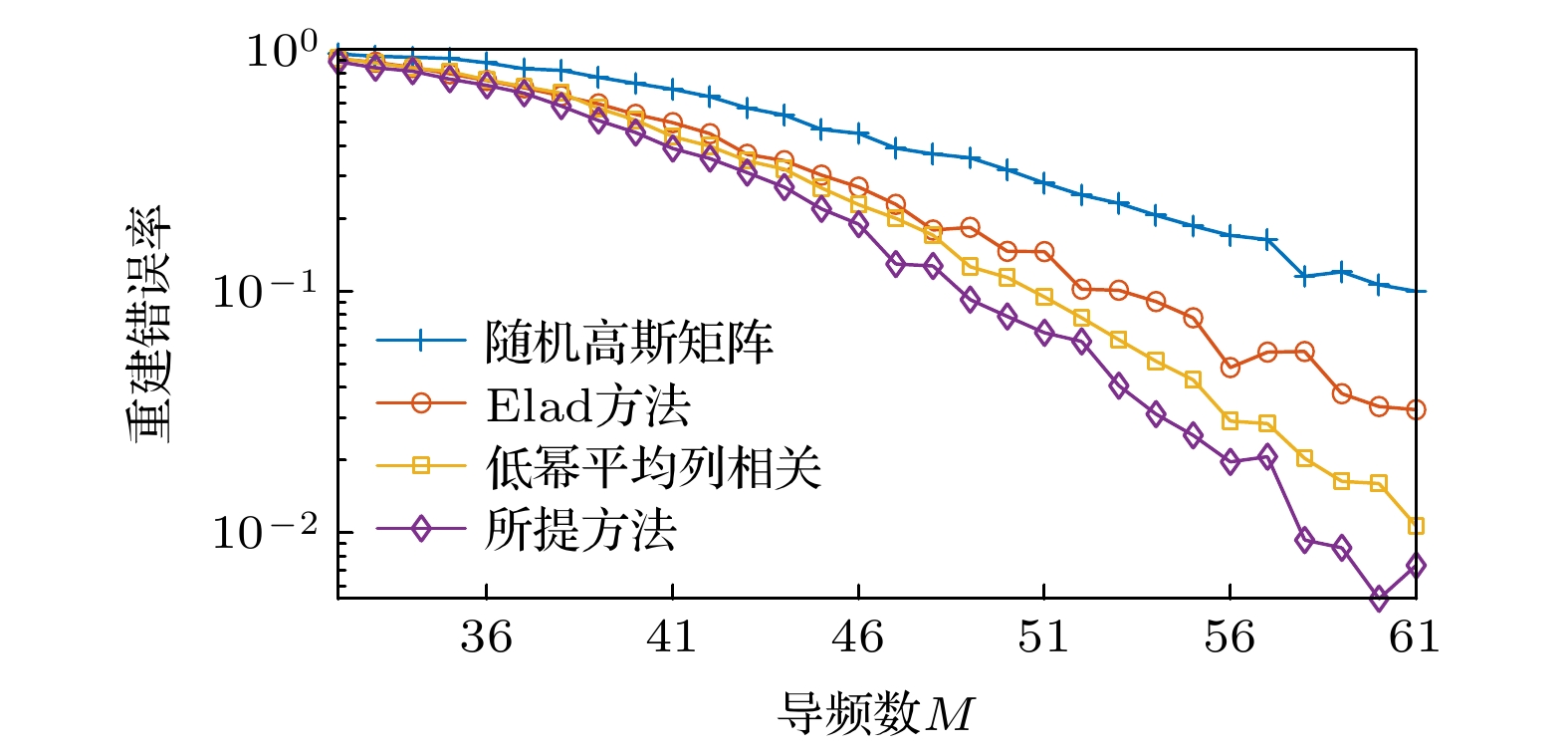
-
针对大规模多输入多输出(multiple input multiple output, MIMO)系统信道估计中的导频设计问题, 在压缩感知理论框架下, 提出了一种基于信道重构错误率最小化的自适应自相关矩阵缩减参数导频优化算法. 首先以信道重构错误率最小化为目标, 推导了正交匹配追踪(orthogonal matching pursuit, OMP)算法下信道重构错误率与导频矩阵列相关性之间的关系, 并得出优化导频矩阵的两点准则, 即导频矩阵列相关性期望和方差最小化; 然后研究了优化导频矩阵的方法, 并提出相应的自适应自相关矩阵缩减参数导频矩阵优化算法, 即在每次迭代过程中, 以待优化矩阵平均列相关程度是否减小作为判断条件, 调整自相关矩阵缩减参数值, 使参数不断趋近于理论最优. 仿真结果表明, 与采用Gaussian矩阵、Elad方法、低幂平均列相关方法得到的导频矩阵相比, 本文所提方法具有更好的列相关性, 且具有更低的信道重构错误率.Aiming at the pilot design problem in channel estimation of large-scale multiple input multiple output (MIMO) systems, an adaptive autocorrelation matrix reduction parameter pilot optimization algorithm based on channel reconstruction error rate minimization is proposed under the framework of compression perception theory. Firstly, the system model and orthogonal matching pursuit (OMP) algorithm are introduced. Secondly, for minimizing the channel reconstruction error rate, the relation between the expected value of the correlation decision in each iteration of the OMP algorithm and the reconstruction error rate is analyzed. For the optimal expected value of the correlation decision, the relation between the channel reconstruction error rate and the correlation of the pilot matrix column under the OMP algorithm is derived, and the two criteria of optimizing the pilot matrix are obtained: the pilot matrix column correlation expectation and the variance minimization. Then the method of optimizing the pilot matrix is studied, and the corresponding adaptive autocorrelation matrix reduction parameter pilot matrix optimization algorithm is proposed. In each iteration, whether the average column correlation degree of the matrix to be optimized is reduced is used as a judgment condition. The autocorrelation matrix reduction parameter value is adjusted to make the parameters close to the theoretical optimization. The simulation results show that the proposed method has a better column correlation property and lower channel reconstruction error rate than the pilot matrix obtained, separately, by Gaussian matrix, Elad method and low power average column correlation method.
-
Keywords:
- massive multiple input multiple output /
- compression sensing /
- channel estimation /
- pilot design
[1] 李贵勇, 于敏, 余永坤 2021 系统工程与电子技术 43 11
Google Scholar
Li G Y, Yu M, Yu Y K 2021 J. Syst. Eng. Electron. 43 11
Google Scholar
[2] 王莉杰, 姜恩华 2021 廊坊师范学院学报 (自然科学版) 21 17
Wang L J, Jiang E H 2021 J. Lang. Nor. Univ. (Nat. Sci. Ed.) 21 17
[3] Sadeghi N, Azghani M 2020 IEEE Trans. Circuits Syst. 100 102640
[4] Elad M 2007 IEEE Trans. Signal Process. 55 5695
Google Scholar
[5] Xu J P, Pi Y M, Cao Z J 2010 Adv. Signal Process. 15 60349
[6] Abolghasemi V, Ferdowsi S, Sanei S 2012 Signal Process. 92 999
Google Scholar
[7] Thompson A, Calderbank R 2017 IEEE Global Conference on Signal and Information Processing (Global SIP), Montreal, QC, 2017 p868
[8] 李哲涛, 潘田, 朱更明, 裴廷睿 2014 电子学报 42 1360
Google Scholar
Li Z T, Pan T, Zhu G M, Pei T R 2014 Acta Electron. Sin. 42 1360
Google Scholar
[9] Sharifi A A, Azarnia G 2020 Optoelectron. Lett. 16 216
Google Scholar
[10] 许波, 王振宇 2020 电气电子教学学报 42 52
Google Scholar
Xu B, Wang Z Y 2020 J. Elect. Elec. Edu. 42 52
Google Scholar
[11] Rahman M L, Zhang J A, Huang X J, Guo Y J, Lu Z P 2021 IET Commun. 14 3977
[12] Meng Z, Pan Z, Shi Y, Chen Z 2019 Multimed. Tools Appl. 78 33969
Google Scholar
[13] Adnan S, Fu Y, Chen Z, Junejo N, Esmaiel H 2019 IET Commun. 13 3472
Google Scholar
[14] 李峰, 郭毅 2015 压缩感知浅析 (北京: 科学出版社) 第20—35页
Li F, Guo Y 2015 Analysis of Compressed Sensing (Beijing: Science Press) pp20–35 (in Chinese)
[15] Datta S, Howard S, Cochran D 2012 Linear Alg. Appl. 437 2455
Google Scholar
[16] Jian L, Peter S 1995 Adaptive Filtering Approach to Spectral Estimation and SAR Imaging (Orlando: International Society for Optics and Photonics) p15
-
图 2 不同参数
$ p $ 定义下的导频矩阵相关性对比Fig. 2. Pilot matrix correlation contrast as defined by different parameters.
图 3 导频矩阵相关性随发送导频数变化图
Fig. 3. Changes of the pilot matrix correlation with the number of transmitted pilots.
图 6 信道重构错误率随导频个数变化图(K=8)
Fig. 6. Channel reconstruction error rate with number of pilots (K=8).
图 7 信道重构错误率随导频个数变化图(K=16)
Fig. 7. Channel reconstruction error rate with number of pilots (K=16).
表 1 仿真参数
Table 1. Simulation parameters.
名称 参数 天线数N/个 128 发送导频数M/个 64 相关性对比参数p 1—20 信道稀疏度K 8 调整因子α 0.5 抽样次数T 3000 错误阈值ξ 0.1 
下载: 导出CSV
-
[1] 李贵勇, 于敏, 余永坤 2021 系统工程与电子技术 43 11
Google Scholar
Li G Y, Yu M, Yu Y K 2021 J. Syst. Eng. Electron. 43 11
Google Scholar
[2] 王莉杰, 姜恩华 2021 廊坊师范学院学报 (自然科学版) 21 17
Wang L J, Jiang E H 2021 J. Lang. Nor. Univ. (Nat. Sci. Ed.) 21 17
[3] Sadeghi N, Azghani M 2020 IEEE Trans. Circuits Syst. 100 102640
[4] Elad M 2007 IEEE Trans. Signal Process. 55 5695
Google Scholar
[5] Xu J P, Pi Y M, Cao Z J 2010 Adv. Signal Process. 15 60349
[6] Abolghasemi V, Ferdowsi S, Sanei S 2012 Signal Process. 92 999
Google Scholar
[7] Thompson A, Calderbank R 2017 IEEE Global Conference on Signal and Information Processing (Global SIP), Montreal, QC, 2017 p868
[8] 李哲涛, 潘田, 朱更明, 裴廷睿 2014 电子学报 42 1360
Google Scholar
Li Z T, Pan T, Zhu G M, Pei T R 2014 Acta Electron. Sin. 42 1360
Google Scholar
[9] Sharifi A A, Azarnia G 2020 Optoelectron. Lett. 16 216
Google Scholar
[10] 许波, 王振宇 2020 电气电子教学学报 42 52
Google Scholar
Xu B, Wang Z Y 2020 J. Elect. Elec. Edu. 42 52
Google Scholar
[11] Rahman M L, Zhang J A, Huang X J, Guo Y J, Lu Z P 2021 IET Commun. 14 3977
[12] Meng Z, Pan Z, Shi Y, Chen Z 2019 Multimed. Tools Appl. 78 33969
Google Scholar
[13] Adnan S, Fu Y, Chen Z, Junejo N, Esmaiel H 2019 IET Commun. 13 3472
Google Scholar
[14] 李峰, 郭毅 2015 压缩感知浅析 (北京: 科学出版社) 第20—35页
Li F, Guo Y 2015 Analysis of Compressed Sensing (Beijing: Science Press) pp20–35 (in Chinese)
[15] Datta S, Howard S, Cochran D 2012 Linear Alg. Appl. 437 2455
Google Scholar
[16] Jian L, Peter S 1995 Adaptive Filtering Approach to Spectral Estimation and SAR Imaging (Orlando: International Society for Optics and Photonics) p15
下载:
计量
- 文章访问数: 5558
- PDF下载量: 102
- 被引次数: 0
