下载:
-
自从反散射变换(IST)方法[1]建立以来, IST可积系统(可以用IST方法求解的系统)的研究引起了物理学界和数学界的高度重视. 从而, 可积系统的各种美妙和谐的性质被发掘出来. 如IST可积系统通常同时具有无穷多对称性和守恒律[2-5]、优美的解析行为(Painlevé性质)[6-10]、Hirota双线性形式和τ 函数 [11]、达布变换和贝克隆变换及非线性叠加原理[12-14]、双哈密顿结构和递推算子[3,15]等. 可积系统也被成功地推广到了离散可积系统[16,17] 和超对称可积系统[18,19]. 同时可积系统及其相应的孤子理论被广泛应用到了物理学的各个领域, 如凝聚态物理[20,21]、粒子物理和核物理[22]、场论[23]、宇宙学[24]、流体力学[25]、光学[26]和等离子体物理等[27]. 然而, 过去的研究主要集中在(1+1)维或(2+1)维等所谓的低维可积系统, 主要原因在于高维可积系统极其稀缺.
从一个复杂系统简化到一个简单系统有很多有效的方法, 如极限法将一些任意的参数取某些特殊极限, 对称法将微分方程的维度或阶数降低等. 要从一个简单系统的结果探索到复杂系统的规律则要困难得多. 幸运的是, 在很多情况下, 将一个简单系统的结果形变到复杂系统也是有可能的. 例如可以将
$ \phi4 $ 方程某些类型的特解形变到$ \phi6 $ 方程的解[28]. ϕ4方程和ϕ6方程分别表示为$ \Box \phi =\sigma \phi+\lambda \phi^3,\ \Box \equiv \partial_t^2-\sum\limits_{i = 1}^D\partial_{x_i}^2 ,$ $ \Box \phi=\sigma \phi+\lambda \phi^3+\xi \phi^5. $ 也可将sine-Gordon (sG)方程
$ \Box \phi= m \sin \phi $ 的某些类型解形变到双sG方程$\Box \phi= m \sin \phi+ n\sin (2\phi)$ 的解[29]. 又如, 利用Korteweg-de Vries (KdV)方程到修正KdV (MKdV) 方程以及Schwartz KdV (SKdV)方程的Miura型变换, 可以从(0+1)维的Riccati方程得到(1+1)维和(2+1)维的可积sG方程[30].最近, 为了得到在各种传统可积意义下更多的高维可积系统, 我们提出了一种形变术, 使得任意的低维可积系统可以被推广到更高维的可积系统[31]. 文献[31]具体给出了(1+1)维KdV方程到(3+1)维KdV-HD系统, 以及从(1+1)维AKNS (Ablowitz-Kaup-Newell-Segue)系统到(2+1)维AKNS系统的形变步骤和结果, 发现新的高维可积系统与传统的可积系统具有完全不同的结构和性质. 虽然新模型具有Lax对、无穷多对称性等好的性质, 但由于原模型及其数个互反系统被包含于同一个模型, 使得传统可积系统的研究方法无法再顺利应用于新模型. 因此, 为了更好地深入研究这一类全新的可积系统, 本文将对另一重要的(1+1)维物理模型, Kaup-Newll (KN)系统[32]进行更高维的推广研究. KN系统为
$ \begin{split} &u_t=u_{xx}+2(u^2v)_x,\\ &v_t=-u_{xx}+2(v^2u)_x. \end{split} $ KN系统是第一类导数非线性薛定谔(DNLS-I)方程的推广(与DNLS-II (Chen-Lee-Liu)系统和DNLS-III (Gerdjikov-Ivanov)系统对应). DNLS-I对应KN系统(1)式的
$u=U(x, \ \tau), \ v=\text{i}u^*, \ \tau=\text{i}t$ , i为复数.本文第2节介绍一般的形变方法. 第3节将形变方法应用到KN系统, 利用KN系统的3个守恒律引进额外的三维新空间坐标, 从而得到一个(4+1)维的KN系统. 将形变方法应用于(1+1)维的KN系统的Lax对, 即可得到(4+1)维KN系统的Lax对. 同样将形变方法应用到(1+1)维的KN系统的高阶流, 能得到(4+1)维KN系统的高阶可积流, 从而得到(4+1)维KN系统的高阶对称. 第4节研究(4+1)维KN系统的各种低维约化. 第5节给出一个(2+1)维互反型导数非线性薛定谔方程的行波孤子解. 第6节是总结和讨论.
-
在文献[31]中, 我们提出了下述形变猜想.
形变猜想: 对于一个任意的(1+1)维m分量n阶演化型局域Lax可积(具有Lax对)或者对称可积(具有无穷多高阶对称)的可积系统
$ \begin{split}& {\boldsymbol u}_t={\boldsymbol F}({\boldsymbol u},\ {\boldsymbol u}_x,\ \ldots,\ {\boldsymbol u}_{xn}),\ \\ &{\boldsymbol u}_{xj}\equiv \partial_{x}^j {\boldsymbol u},\ {\boldsymbol u}=(u_1,\ u_2,\ \ldots,\ u_m), \end{split} $ 如果存在D – 1个守恒律
$ \begin{split} &[\rho_{i}({\boldsymbol u})]_t=[J_{i}({\boldsymbol u},\ {\boldsymbol u}_x,\ \cdots,\ {\boldsymbol u}_{xN})]_x,\\ &i = 1,\ 2,\ \cdots,\ D-1, \end{split} $ 其中守恒密度
$ \rho_i({\boldsymbol u})\equiv \rho_i $ 仅与场有关, 但与场的空间导数无关, 而守恒流$ J_i $ 可以与场的空间导数有关, 则(D+1)维系统$ \hat{T}{\boldsymbol u}={\boldsymbol F}({\boldsymbol u},\ \hat{L}{\boldsymbol u},\ \cdots,\ \hat{L}^n{\boldsymbol u}), $ 仍然是Lax可积或对称可积的可积系统. 其中空间形变算子
$ \hat{L} $ 和时间形变算子$ \hat{T} $ 定义为$ \begin{split} &\hat{L}=\partial_x+\sum_{i = 1}^{D-1}\rho_i\partial_{x_i},~~~~ \hat{T}=\partial_t+\sum_{i = 1}^{D-1}\bar{J}_i\partial_{x_i},\\ & ~~~~~~ \bar{J}_i\equiv J_{i}({\boldsymbol u},\ \hat{L}{\boldsymbol u},\ \cdots,\ \hat{L}^N{\boldsymbol u}). \end{split}$ 注记: 该猜想已被宁波大学数学与统计学院的张丹达和Matteo Casati所证明. 所以后文中也称该形变猜想为形变定理, 而定理中提出的形变方法为形变术.
如果形变前的(1+1)维可积系统(2)式具有Lax对:
$ \begin{align} \varPhi_x=M \varPhi,\quad \varPhi_t=N \varPhi, \end{align} $ 则形变后的(D+1)维可积系统(4)式的Lax对可以通过将形变术应用到(6)式来得到, 即
$ \begin{split}& \hat{L}\varPhi=\hat{M} \varPhi,\quad \hat{T}\varPhi=\hat{N} \varPhi,\\ &\{\hat{M},\ \hat{N}\}\equiv \left.\{M,\ N\}\right|_{\partial_x\rightarrow \hat{L},\ u_{xj}\rightarrow (\hat{L}^ju)}. \end{split} $ 通常(1+1)维可积系统是对称可积的, 即存在无穷多高阶对称. 要得到(D+1)维可积系统(4)式的高阶对称, 不能直接将形变术应用到(1+1)维可积系统(2)式的高阶对称. 需要将(1+1)维可积系统(2)式的高阶对称对应的流方程写出来, 如
$ \begin{align} {\boldsymbol u}_{\tau}={\boldsymbol G}({\boldsymbol u},\ {\boldsymbol u}_x,\ \ldots,\ {\boldsymbol u}_{x(n+p)}),\quad p > 0. \end{align} $ 此时, 需要算出(8)式与(2)式相同守恒密度
$ \rho_i $ 对应的守恒律$ \begin{split} &[\rho_i({\boldsymbol u})]_{\tau}=[K_{i}({\boldsymbol u},\ {\boldsymbol u}_x,\ \cdots,\ {\boldsymbol u}_{xM})]_x\equiv K_{ix},\\ & ~~~~~~ i = 1,\ 2,\ \cdots,\ D-1. \end{split} $ 然后, 将形变术应用到(8)式可得
$ \begin{split} {\boldsymbol u}_{\tau}=\;&\left.{\boldsymbol G}({\boldsymbol u},\ {\boldsymbol u}_x,\ \ldots,\ {\boldsymbol u}_{x(n+p)})\right|_{{\boldsymbol u}_{xj}\rightarrow \hat{L}^j{\boldsymbol u}}\\ &-\sum_{j = 1}^{D-1}\bar{K}_j{\boldsymbol u}_{x_j}\equiv \bar{{\boldsymbol G}}, \end{split} $ 其中
$ \bar{K}_j $ 是$ K_j $ 的形变流,$ \bar{K}_j=\left.K_j\right|_{{\boldsymbol u}_{xi}\rightarrow \hat{L}^i{\boldsymbol u}} $ . 因此,$ \bar{{\boldsymbol G}} $ 是(D+1)维方程(4)的高阶对称. 对所有(1+1)维系统的所有高阶流应用形变术即可得到方程(4)的整个可积梯队. -
很容易验证, (1+1)维KN系统(1)式具有满足形变术条件的守恒密度
$ u, \ v $ 和$ uv $ , 相应的守恒流为$ J_1=u_x+2 u^2 v, \ J_2=-v_x+2 v^2 u $ 及$J_3=vu_x- uv_x+3 u^2 v^2$ . 根据形变定理, 可以引入空间和时间形变算子:$ \begin{split} &\hat{L}_{{\rm{KN}}}=\partial_x+u\partial_y+v\partial_z+uv\partial_{\xi},\\ &\hat{T}_{{\rm{KN}}}=\partial_t+\bar{J}_1\partial_y+\bar{J}_2\partial_z+\bar{J}_3\partial_{\xi}, \end{split} $ 其中形变流为
$ \begin{split} &\bar{J}_{1}=u_x+uu_y+vu_z+uvu_{\xi}+2u^2v,\\ &\bar{J}_{2}=-v_x-uv_y-vv_z-uvv_{\xi}+2v^2u,\\ &\bar{J}_{3}=v(u_x+uu_y+vu_z+uvu_{\xi})\\ &\qquad-u(v_x+uv_y+vv_z+uvv_{\xi})+3u^2v^2. \end{split} $ 利用形变算子(11)式和形变术, 可得(4+1)维的可积KN系统:
$ \begin{split} &\hat{T}_{{\rm{KN}}}u=\hat{L}_{{\rm{KN}}}\bar{J}_1=\hat{L}_{{\rm{KN}}}(\hat{L}_{{\rm{KN}}}u+2u^2v),\\ &\hat{T}_{{\rm{KN}}}v=\hat{L}_{{\rm{KN}}}\bar{J}_2=\hat{L}_{{\rm{KN}}}(-\hat{L}_{{\rm{KN}}}v+2v^2u). \end{split} $ (13)式的详细展开式为
$ \begin{split} u_t=\;&u_{xx}+2uvu_{x\xi}+2uu_{xy}+2vu_{xz}+u^2v^2 u_{\xi\xi}+2u^2vu_{y\xi}+2uv^2u_{z\xi} +u^2u_{yy}+2uvu_{yz}+v^2u_{zz}\\ &+uv(uvu_{\xi}+2uu_y+2vu_z+4u_x)+ (2u^2+2uu_{\xi}+2u_z)(uvv_{\xi}+uv_y+vv_z+v_x),\\ v_t=\;&-v_{xx}-2uvv_{x\xi}-u^2v^2 v_{\xi\xi}-2 u^2vv_{y\xi}-2 uv^2v_{z\xi}-2uvv_{yz}-2uv_{xy}-2vv_{xz}-u^2v_{yy}-v^2 v_{zz}\\ & +uv(uvv_{\xi}+2uv_y+2vv_z+4v_x)+(2v^2-2vv_{\xi}-2v_y)(uvu_{\xi}+uu_y+vu_z+u_x). \end{split} $ -
众所周知, (1+1)维KN系统[32]是Lax可积的, 其Lax对为
$ \begin{eqnarray} \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right)_x &= & 2\lambda\left(\begin{array}{cc} \lambda & u \\ -v & -\lambda \end{array}\right) \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right), \end{eqnarray} $ $ \begin{eqnarray} \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right)_t &= & 2\lambda\left(\begin{array}{cc} 2\lambda(2\lambda^2+uv) & 2u(2\lambda^2+uv)+u_x \\ -2v(2\lambda^2+uv)+v_x & -2\lambda(2\lambda^2+uv) \end{array}\right) \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right). \end{eqnarray} $ 将形变术应用到(15)式和(16)式, 即得(4+1)维KN系统(13)式或(14)式的Lax对为(
$ w\equiv 2\lambda^2+uv $ )$ \begin{eqnarray} \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right)_x &= & \left(\begin{array}{cc} 2\lambda^2-u\partial_y-v\partial_z-uv\partial_{\xi} & 2\lambda u \\ -2\lambda v & -2\lambda^2-u\partial_y-v\partial_z-uv\partial_{\xi} \end{array}\right) \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right), \end{eqnarray} $ $ \begin{eqnarray} \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right)_t &= & \left(\begin{array}{cc} 4\lambda^2w-\bar{J}_1\partial_y-\bar{J}_2\partial_z-\bar{J}_3\partial_{\xi} & 4\lambda uw+2\lambda (\hat{L}_{KN}u) \\ -4\lambda vw+2\lambda (\hat{L}_{KN}v) & -4\lambda^2w-\bar{J}_1\partial_y-\bar{J}_2\partial_z-\bar{J}_3\partial_{\xi} \end{array}\right) \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right). \end{eqnarray} $ $ \begin{align} \hat{{\boldsymbol{M}}}{\boldsymbol{\varPhi}} = 0,\qquad \hat{{\boldsymbol{N}}}{\boldsymbol{\varPhi }}= 0, \end{align} $ 其中,
$ \begin{eqnarray} && \hat{{\boldsymbol{M}}}\equiv \left(\begin{array}{cc} 2\lambda^2-\hat{L}_{{\rm{KN}}} & 2\lambda u \\ -2\lambda v & -2\lambda^2-\hat{L}_{{\rm{KN}}} \end{array}\right),\quad {\boldsymbol{\varPhi}}\equiv \left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right), \end{eqnarray} $ $ \begin{eqnarray} && \hat{{\boldsymbol{N}}}\equiv \left(\begin{array}{cc} 4\lambda^2w-\hat{T}_{{\rm{KN}}} & 4\lambda uw+2\lambda (\hat{L}_{{\rm{KN}}}u) \\ -4\lambda vw+2\lambda (\hat{L}_{{\rm{KN}}}v) & -4\lambda^2w-\hat{T}_{{\rm{KN}}} \end{array}\right). \end{eqnarray} $ Lax对的相容性条件为
$ \begin{align} [\hat{{\boldsymbol{M}}}, \hat{{\boldsymbol{N}}}]=\hat{{\boldsymbol{M}}}\hat{{\boldsymbol{N}}}-\hat{{\boldsymbol{N}}}\hat{{\boldsymbol{M}}} = 0 ,\end{align} $ -
和其他Lax可积系统一样, (1+1)维KN系统是对称可积的, 即具有高阶对称性. 其最简单的高阶对称对应的流方程为
$ \begin{split}& u_{\tau}=K_{1x},\ \quad K_1=u_{xx}+6uvu_x+6u^3v^2, \\ &v_{\tau}=K_{2x},\ \quad K_2=v_{xx}-6uvv_x+6u^2v^3. \end{split} $ 对应于高阶流方程(23)的导数无关守恒密度除了u和v外, 还有
$ uv $ 及相应的守恒律为$ \begin{split} &(uv)_{\tau}=K_{3x},\\ &K_3=vu_{xx}+uv_{xx}-u_xv_x+6v^2uu_x\\ &\qquad-6u^2vv_x+10u^3v^3. \end{split} $ 将形变术应用于高阶流方程, 需要引入τ对应的形变算子
$ \hat{\tau} $ :$ \begin{eqnarray} \hat{\tau}=\partial_{\tau}+\bar{K}_1\partial_y+\bar{K}_2\partial_z+\bar{K}_3\partial_{\xi}, \end{eqnarray} $ 其中形变的守恒流
$ \bar{K}_1, \ \bar{K}_2 $ 和$ \bar{K}_3 $ 为$ \begin{split} \bar{K}_1=\;&\hat{L}_{{\rm{KN}}}^2u+6uv\hat{L}_{{\rm{KN}}}u+6u^3v^2, \\ \bar{K}_2=\;&\hat{L}_{{\rm{KN}}}^2v-6uv\hat{L}_{{\rm{KN}}}v+6u^2v^3,\\ \bar{K}_3=\;&v\hat{L}_{{\rm{KN}}}^2u+u\hat{L}_{{\rm{KN}}}^2v-(\bar{L}_{{\rm{KN}}}u)(\bar{L}_{{\rm{{\rm{KN}}}}}v)\\ &+6v^2u\hat{L}_{{\rm{KN}}}u-6u^2v\hat{L}_{{\rm{KN}}}v+10u^3v^3. \end{split} $ 由此可得(4+1)维的高阶流方程为
$ \begin{split} &\hat{\tau}u=\hat{L}_{{\rm{KN}}}\bar{K}_{1}, \\ &\hat{\tau}v=\hat{L}_{{\rm{KN}}}\bar{K}_{2}. \end{split} $ 从高阶流方程可得(4+1)维KN方程(13), 也就是方程(14)的高阶对称为
$ \begin{eqnarray} {\boldsymbol{\sigma}}=\left(\begin{array}{c} \hat{L}_{{\rm{KN}}}\bar{K}_{1}-\bar{K}_{1}u_y-\bar{K}_{2}u_z-\bar{K}_{3}u_{\xi}\\ \hat{L}_{{\rm{KN}}}\bar{K}_{2}-\bar{K}_{1}v_y-\bar{K}_{2}v_z-\bar{K}_{3}v_{\xi}\end{array}\right) .\end{eqnarray} $ -
为更清楚地看清(4+1)维KN系统(14)式的新特点, 下面讨论其低维约化的性质. 显然, 当
$ \{u, \ v\} $ 与$ \{y, \ z, \ \xi\} $ 无关时, (4+1)维KN系统(13)式退化为原来的(1+1)维KN系统. 因此, 原(1+1)维KN 系统(1)式的所有解仍然是(4+1)维KN系统的特解. 因此, 这里不讨论这种平凡特例. -
当
$ \{u, \ v\} $ 与$ \{x, \ z, \ \xi\} $ 无关时, (4+1)维KN系统(13)式退化为(1+1)维KN系统(1)式的第一类互反形式:$ \begin{split} &u_t=u^2u_{yy}+2u^2vu_y+2u^3v_y,\\ &v_t=-u^2v_{yy}-2uu_yv_y+2u^2vv_y+2v^2uu_y. \end{split} $ (1+1)维互反KN系统(29)式的Lax对为
$ \begin{split} &\hat{{\boldsymbol{M}}}_y{\boldsymbol{\varPhi}}\equiv \left(\begin{array}{cc} u\partial_y-2\lambda^2 & -2\lambda u\\ 2\lambda v & u\partial_y+2\lambda^2 \end{array}\right)\left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right) = 0, \\ &\hat{{\boldsymbol{N}}}_y{\boldsymbol{\varPhi}}\equiv \left(\begin{array}{cc} \partial_t +u (2 u v+u_y) \partial_y-4 \lambda^2 w & -2\lambda u(2w+u_y) \\ -2\lambda (v_y-2vw) & \partial_t +u (2 u v+u_y) \partial_y+4 \lambda^2 w \end{array}\right)\left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right) = 0. \end{split} $ (30)式的相容性条件
$[\hat{{\boldsymbol{M}}}_y, \ \hat{{\boldsymbol{N}}}_y] = 0$ 正是(1+1)维互反KN系统(29)式.显然, (1+1)维模型(29)式符合形变定理, 因此, 可以将形变术应用到(29)式以得到可能的新高维模型. 为此, 须先研究(29)式的守恒律. 容易验证, (29)式具有下述守恒律:
$ \begin{split} &v_t=(-u^2v_{y}+u^2v^2)_y,\\ &(u^{-1})_t=(-u_y-2uv)_y,\\& (vu^{-1})_t=(uv)_{yy}. \end{split} $ 根据守恒律(31)式, 可以引入空间y和时间t的形变算子:
$ \begin{split} \hat{L}_y=\;&\partial_y+u^{-1}\partial_x+vu^{-1}\partial_z+v\partial_{\xi},\\ \hat{T}_y=\;&\partial_t-(\hat{L}_yu+2uv)\partial_x+\hat{L}_y(vu)\partial_z\\ &+u^2(v^2-\hat{L}_yv)\partial_{\xi}. \end{split} $ 由此, 根据形变定理, 第一类互反KN系统(29)式的(4+1)维可积形变具有下述形式:
$ \begin{split}& \hat{T}_yu=u^2\hat{L}_y^2u+2u^2v\hat{L}_yu+2u^3\hat{L}_yv,\\ &\hat{T}_yv=\hat{L}_y[u^2(v^2-\hat{L}_yv)]. \end{split} $ 既巧合也合理的是, 将(32)式代入(33)式, 展开整理后可以发现结果与(14)式完全相同. 由于(33)式与(13)式的全同性, 不再讨论(33)式的Lax可积性和对称可积性.
-
当模型仅与
$ \{z, \ t\} $ 有关时, (4+1)维KN系统(13)式约化成第二类(1+1)维互反KN系统:$ \begin{split} &u_t=v^2u_{zz}+2uv^2u_z+2v(u^2+u_z)v_z,\\ &v_t=-v^2 v_{zz}+2uv^2v_z+2v^3u_z. \end{split} $ 第二类(1+1)维互反KN系统的满足形变术要求的守恒律, 有
$ \begin{split} &u_t=(v^2u_z+u^2v^2)_z,\\ &(v^{-1})_t=(v_z-2uv)_z,\\ &(uv^{-1})_t=(uv)_{zz}. \end{split} $ 由此可以引入时空形变算子:
$ \begin{split} \hat{L}_z=\;&\partial_z+v^{-1}\partial_x+uv^{-1}\partial_y+u\partial_{\xi},\\ \hat{T}_z=\;&\partial_t+(\hat{L}_zv-2uv)\partial_x+\hat{L}_z(vu)\partial_y\\ &+v^2(u^2+\hat{L}_zu)\partial_{\xi}. \end{split} $ 从而, (34)式的(4+1)维的可积形变为
$ \begin{split}& \hat{T}_zu=v^2\hat{L}_z^2u+2uv^2\hat{L}_zu+2v[u^2+(\hat{L}_zu)]\hat{L}_zv,\\ &\hat{T}_zv=-v^2 \hat{L}_z^2v+2uv^2\hat{L}_zv+2v^3\hat{L}_zu.\\[-12pt] \end{split} $ -
当模型与
$ \{x, \ y, \ z\} $ 无关时, (4+1)维KN系统(13)式约化成第三类(1+1)维互反KN系统:$ \begin{split}& u_t=u^2v^2 (u_{\xi\xi}+u_{\xi})+ 2vu^2(u+u_{\xi})v_{\xi},\\ &v_t=u^2v^2(v_{\xi}- v_{\xi\xi})+2uv^2(v-v_{\xi})u_{\xi}. \end{split} $ 和第一类与第二类的(1+1)维互反KN系统所不同的是, 第三类的(1+1)维互反KN系统和原(1+1)维KN系统一样, u和v有一定的互换对称性. 第三类(1+1)维互反KN系统(38)式的Lax对具有下述形式:
$ \begin{split} &\hat{{\boldsymbol{M}}}_{\xi}{\boldsymbol{\varPhi}}\equiv \left(\begin{array}{cc} uv\partial_{\xi}-2\lambda^2 & -2\lambda u\\ 2\lambda v & uv\partial_{\xi}+2\lambda^2 \end{array}\right)\left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right) = 0, \\ &\hat{{\boldsymbol{N}}}_{\xi}{\boldsymbol{\varPhi}}\equiv \left(\begin{array}{cc} \partial_t +uv (3 u v+vu_{\xi}-uv_{\xi}) \partial_{\xi}-4 \lambda^2 w & -2\lambda u(2w+vu_{\xi}) \\ -2\lambda v(uv_{\xi}-2w) & \partial_t +uv (3 u v+vu_{\xi}-uv_{\xi}) \partial_{\xi}+4 \lambda^2 w \end{array}\right)\left(\begin{array}{c} \phi_1 \\ \phi_2 \end{array}\right) = 0. \end{split} $ (39)式的相容性条件
$ [\hat{{\boldsymbol{M}}}_{\xi}, \ \hat{{\boldsymbol{N}}}_{\xi}] = 0 $ 正是第三类(1+1)维互反KN系统(38)式.第三类(1+1)维互反KN系统(38)式具有满足形变术的下述守恒律:
$ \begin{split}&(u^{-1})_t=-(v^2u_{\xi}+uv^2)_{\xi},\\ &(v^{-1})_t=(u^2v_{\xi}-u^2v)_{\xi},\\ &(u^{-1}v^{-1})_t=(uv_{\xi}-vu_{\xi}-3uv)_{\xi}. \end{split} $ 从上述守恒律, 可以引入下述空时形变算子:
$ \begin{split} \hat{L}_{\xi}=\;&\partial_{\xi}+u^{-1}\partial_z+v^{-1}\partial_y+u^{-1}v^{-1}\partial_x,\\ \hat{T}_{\xi}=\;&\partial_t-[v^2(\hat{L}_{\xi}u)+uv^2]\partial_z+[u^2(\hat{L}_{\xi}v)-u^2v]\partial_y \\ &+[u(\hat{L}_{\xi}v)-v(\hat{L}_{\xi}u)-3uv]\partial_x. \\[-10pt] \end{split} $ 利用空时形变算子
$ \hat{L}_{\xi} $ 和$ \hat{T}_{\xi} $ , 第三类(1+1)维互反KN系统(38)式可被形变到一个(4+1)维KN系统:$ \begin{split}& \hat{T}_{\xi}u=u^2v^2 (\hat{L}_{\xi}^2u+\hat{L}_{\xi}u)+ 2vu^2[u+(\hat{L}_{\xi}u)]\hat{L}_{\xi}v,\\ &\hat{T}_{\xi}v=u^2v^2(\hat{L}_{\xi}v-\hat{L}_{\xi}^2 v)+2uv^2[v-(\hat{L}_{\xi}v)]\hat{L}_{\xi}u. \end{split} $ 毫不奇怪也不难直接展开验证, (4+1)维KN系统(42)式和(14)式完全相同. 至此得到了(4+1)维KN系统(14)式的4个用不同形变算子表示的等价表达式——(13)式、(33)式、(37)式和(42)式.
-
对于(4+1)维KN系统(13)式的(2+1)维约化, 直接列出6种非平庸的约化.
约化 1 (1+1)维KN系统(1)式与第一类互反KN系统(29)式的可积组合:
$ \begin{split} u_t =\;& (2u^2v+2uu_y+u_x)_x+(2u^3v+u^2u_y)_y\\ &-2u_y(2u^2v+uu_y+u_x),\\ v_t =\;& (2uv^2-2uv_y-v_x)_x+(u^2v^2-u^2v_y)_y. \end{split} $ 约化 2 (1+1)维KN系统(1)式与第二类互反KN系统(34)式的可积组合:
$ \begin{split} u_t =\;& (2u^2v+2vu_z+u_x)_x+(u^2v^2+u_zv^2)_z,\\ v_t =\;&(2uv^2-2vv_z-v_x)_x+(2uv^3-v^2v_z)_z\\ &-2v_z(2uv^2-vv_z-v_x). \end{split} $ 约化 3 (1+1)维KN系统(1)式与第三类互反KN系统(38)式的可积组合:
$ \begin{split} u_t =\;& (u_x+2uvu_{\xi}+2u^2v)_x \\ &+(u_{\xi}u^2v^2+u^3v^2)_{\xi}\\ &-2vu_{\xi}(u^2v+uvu_{\xi}+u_x),\\ v_t =\;&(2uv^2-v_x-2uvv_{\xi})_x \\ & +(u^2v^3-v_{\xi}u^2v^2)_{\xi}\\ &+2uv_{\xi}(uvv_{\xi}-uv^2+v_x). \end{split} $ 我们知道原(1+1)维KN系统(1)式存在一种导数非线性薛定谔约化. 仔细分析可以发现, (4+1)维方程一般情况下已经不存在这种类型的约化. 然而, 有意义的是, (2+1)维约化(45)式仍然具有类似的约化. 为此, 对(45)式作下述变换:
$ \begin{split} &u(x,\ \xi,\ t)=p(x,\ \text{i}\xi,\ \text{i}t),\\ &v(x,\ \xi,\ t)=\text{i} q(x,\ \text{i}\xi,\ \text{i}t),~~ \ \text{i}=\sqrt{-1}. \end{split} $ $ \begin{split} q_t=\;&(\text{i}q_x-2\text{i}pqq_y+2q^2p)_x+(\text{i}p^2q^2q_y-p^2q^3)_y-2 pq_y(\text{i}pqq_y-q^2p-\text{i}q_x),\\ p_t=\;&(-\text{i}p_x+2\text{i}pqp_y+2p^2q)_x-(\text{i}p^2q^2p_y+p^3q^2)_y+2 qp_y(\text{i}pqp_y+p^2q-\text{i}p_x). \end{split} $ 为了方便, (47)式中的
$ \{\text{i}\xi, \ \text{i}t\} $ 已经被重新标记为$ \{y, \ t\} $ . 显然(47)式允许导数非线性薛定谔型约化,$ p=\pm q^* $ ,$ q_t=(\text{i}q_x\mp 2\text{i}|q|^2q_y\pm 2|q|^2q)_x+(\text{i}|q|^4q_y-|q|^4q)_y\mp 2 q^*q_y(\pm \text{i}|q|^2q_y\mp |q|^2q-\text{i}q_x). $ 约化 4 第一类互反KN系统(29)式与第二类互反KN系统(34)式的可积组合:
$ \begin{split} u_t =\;& (2u^3v+u^2u_y+2uvu_z)_y+(u^2v^2+u_zv^2)_z-2u_y(2u^2v+uu_y+vu_z),\\ v_t =\;& (u^2v^2-u^2v_y)_y+(2uv^3-2uvv_y-v^2v_z)_z-2v_z(2uv^2-uv_y-vv_z). \end{split} $ 约化 5 第一类互反KN系统(29)式与第三类互反KN系统(38)式的可积组合:
$ \begin{split} u_t =\;& (u^2u_y+2u_{\xi}u^2v+2vu^3)_y+(u_{\xi}u^2v^2+u^3v^2)_{\xi}-2uvu_{\xi}(uv+vu_{\xi}+2u_y)-2uu_y(2uv+u_y),\\ v_t =\;& (u^2v^2-u^2v_y-v_{\xi}u^2v)_y+(u^2v^3-v_{\xi}u^2v^2-u^2vv_y)_{\xi} +2v_{\xi}u^2(v_{\xi}v-v^2+v_y). \end{split} $ 约化 6 第二类互反KN系统(34)式与第三类互反KN系统(38)式的可积组合:
$ \begin{split} u_t =\;&(v^2u_z+u_{\xi}uv^2+u^2v^2)_z+(u_{\xi}u^2v^2+uv^2u_z+u^3v^2)_{\xi}-2v^2u_{\xi}(u^2+uu_{\xi}+u_z),\\ v_t =\;&(2uv^3-v_zv^2-2v_{\xi}uv^2)_z-(u^2v^3-v_{\xi}u^2v^2)_{\xi} +2uv v_{\xi}(uv_{\xi}-uv+2v_z)-2vv_z(2uv-v_z). \end{split} $ 本节的(2+1)维约化系统的Lax对均可从(20)式和(21)式直接去掉两个无关变量的导数得到. 例如对于(45)式的约化3, 模型是
$ \{y, \ z\} $ 无关的, 因此其Lax对只要将(20)式和(21)式中的$ \hat{L}_{{\rm{KN}}} $ 和$ \hat{T}_{{\rm{KN}}} $ 作下述替换即可:$ \begin{split} &\hat{L}_{{\rm{KN}}}\rightarrow \hat{L}',\quad \hat{T}_{{\rm{KN}}}\rightarrow \hat{T}',\quad \hat{L}'\equiv\partial_{x}+uv\partial_{\xi},\\ &\hat{T}'\equiv \partial_t+(v\hat{L}'u-u\hat{L}'v+3u^2v^2)\partial_{\xi}. \end{split} $ -
对于(4+1)维KN系统(13)式, 可以找到4种(3+1)维约化, 具体约化结果如下.
第一类(3+1)维互反KN系统是(1+1)维KN系统(1)式、第一类互反KN系统(29)式和第二类互反KN系统(34)式的可积融合:
$ \begin{split}& u_t=(2u^2v+2uu_y+2vu_z+u_x)_x+(2u^3v+u^2u_y+2vuu_z)_y+(u^2v^2+v^2 u_z)_z-2u_y(2u^2v+uu_y+vu_z+u_x),\\ &v_t=(2uv^2-2uv_y-2vv_z-v_x)_x+(u^2v^2-u^2v_y)_y+(2uv^3-2uvv_y-v^2v_z)_z -2v_z(2uv^2-uv_y-vv_z-v_x). \end{split} $ (3+1)维可积互反KN系统(52)式也可以直接利用3个(1+1)维可积KN型系统(1)式、(29)式和(34)式中的任何一个, 以及它们的两个守恒律直接作形变得到.
第二类(3+1)维互反KN系统是(1+1)维KN系统(1)式和第一类互反KN系统(29)式及第三类互反KN系统(38)式的可积融合:
$ \begin{split} u_t=\;&(u_x+2u^2v+2uvu_{\xi}+2uu_y)_x+(u^2u_y+2 u^2vu_{\xi}+2vu^3)_y+(u^2v^2u_{\xi}+u^3v^2)_{\xi}\\ & -2u_y(2u^2v+uu_y+u_x)-2vu_{\xi}(u^2v+uvu_{\xi}+2uu_y+u_x),\\ v_t=\;&(2v^2u-v_x-2uvv_{\xi}-2uv_y)_x+(u^2v^2-u^2v_y-v_{\xi}u^2v)_y+(u^2v^3-u^2v^2v_{\xi}-u^2vv_y)_{\xi}\\ & +2 u v_{\xi}(uvv_{\xi}-v^2u+uv_y+v_x). \end{split} $ (3+1)维可积互反KN系统(53)式也可以直接利用3个(1+1)维可积KN型系统(1)式、(29)式和(38)式中的任何一个, 以及它们的两个相应的守恒律直接作形变得到.
第三类(3+1)维互反KN系统是三类(1+1)维互反KN系统(1)式、(34)式及(38)式的组合, 并加上各组份间的相互作用项以保证可积性:
$ \begin{split} u_t =\;&(u_x+2vu_z+2uvu_{\xi}+2u^2v)_x+(v^2u_z+uv^2u_{\xi}+u^2v^2)_z+(u^2v^2u_{\xi}+uv^2u_z+u^3v^2)_{\xi} \\ & -2vu_{\xi}(u^2v+uvu_{\xi}+vu_z+u_x),\\ v_t=\;&(2v^2u-2vv_z-v_x-2uvv_{\xi})_x+(2uv^3-v^2v_z-2 uv^2v_{\xi})_z+(u^2v^3-u^2v^2 v_{\xi})_{\xi}\\ & +2(u v_{\xi}+v_z)(uvv_{\xi}+vv_z+v_x)-2uv^2(uv_{\xi}+2v_z). \end{split} $ (3+1)维可积互反KN系统(54)式还可以直接利用3个(1+1)维可积KN型系统(1)式、(34)式和(38)式中的任何一个, 以及它们两个相应的守恒律直接利用形变术得到.
第四类(3+1)维互反KN系统是三类(1+1)维互反KN系统(29)式、(34)式及(38)式的可积组合:
$ \begin{split} u_t = \;& (u^2u_y+2 u^2v u_{\xi}+2uvu_z+2vu^3)_y+(v^2u_z+uv^2 u_{\xi}+u^2v^2)_z +(u^2v^2u_{\xi}+uv^2u_z+u^3v^2)_{\xi} \\ & -2vu_{\xi}(u^2v+uvu_{\xi}+2uu_y+vu_z)-2u_y(2u^2v+uu_y+vu_z),\\ v_t =\;& (u^2v^2-u^2v_y-u^2v v_{\xi})_y+(2uv^3-v^2 v_z-2vuv_y-2 uv^2 v_{\xi})_z +(u^2v^3-u^2v^2v_{\xi}-u^2vv_y)_{\xi}\\ & +2uv_{\xi}(uv_y+2vv_z-v^2u+uvv_{\xi})+2v_z(uv_y+vv_z-2uv^2). \end{split} $ (3+1)维可积互反KN系统(55)式可以直接利用3个(1+1)维可积互反KN型系统(29)式、(34)式和(38)式中的任何一个, 并利用形变术来获得.
-
虽然本文提出了大量的新的高维可积的KN互反系统, 然而由于新模型中包含了KN系统及其互反的组合, 因此对这些系统的求解变得极其困难. 本节仅讨论(2+1)维互反型导数非线性薛定谔方程(48)的包络行波解. 对于方程(48), 取定上面的正负号, 即
$ \begin{split} q_t= (\text{i}q_x- 2\text{i}|q|^2q_y+ 2|q|^2q)_x+(\text{i}|q|^4q_y-|q|^4q)_y- 2 q^*q_y( \text{i}|q|^2q_y- |q|^2q-\text{i}q_x). \end{split} $ (56)式的包络行波解可设为
$ \begin{split} &q=Q(X)\exp\{-\text{i}[k_0x+l_0y+\omega_0t+\theta(X)]\},~~~~ X\equiv k_1x+k_2y+\omega t. \end{split} $ 将(57)式代入(56)式, 分离实部和虚部, 并将θ和Q分离即得
$ \begin{split}& \theta_{X}=\frac{c_1}{Q^2}-\frac{2l_0-3}{2k_2} +\frac{2k_0k_1k_2-2l_0k_1^2+3k_1^2-k_2\omega}{2k_2^2Q^2(k_2Q-k_1)},\\ &4Q^3(k_2Q-k_1)^3Q_{XX}+8k_2Q^4(k_2Q-k_1)Q_x^2 +3Q^8+4C_1Q^6+\omega_2Q^4-\omega_1^2 = 0, \end{split} $ 其中
$ c_1 $ 为积分常数;$ C_1, \ \omega_1 $ 和$ \omega_2 $ 定义为$ \begin{split}&C_1 = 2c_1k_2-2k_0+k(2l_0-3),~~~~\omega_1 = 2c_1k_1-2kk_0+\omega k_2^{-1}+k^2(2l_0-3),\end{split} $ $ \begin{split}\omega_2 =\;& 4k_2^2c_1^2-8c_1k_1-4k_0^2+4kk_0(2l_0-1) +4\omega_0 -2\omega(2l_0-1)k_2^{-1}-k^2(4l_0^2-4l_0-3).\end{split} $ (58)式中Q方程的解可以用下述椭圆积分表示:
$ \begin{split} \int^Q\frac{\eta(k_2\eta^2-k_1)}{\sqrt{c_2\eta^2-\eta^8-2C_1\eta^6-\omega_2\eta^4-\omega_1^2}}\text{d}\eta = -\frac{X-X_0}2, \end{split} $ 其中
$ c_2 $ 和$ X_0 $ 为积分常数.为了给出孤子解的表达式, 将任意常数
$ C_1, \ c_2, \ \omega_2 $ 及$ \omega_1 $ 取为$ \begin{split} &C_1 = -a^2-b,~~~~ c_2 = 2a^2(c^2 +a^2b), ~~~~\omega_2 = a^4+4a^2b+c^2,~~~~ \omega_1^2 = c^2a^4. \end{split} $ 当常数满足(60)式的关系时, 椭圆积分解(57)式退化成单孤子解(
$ Q=|q|, \ C=\sqrt{2 a^2 b-a^4-c^2} $ ):$ \begin{align} \frac{C^2(2b|q|^2-|q|^4-c^2)}{[(a^2-b)|q|^2-a^2b+c^2]^2} =\tanh^2\left[\frac{C}{a^2k_2-k_1} \left(k_2\arctan\frac{|q|^2-b}{\sqrt{2b|q|^2-|q|^4-c^2}}+X+X_0\right)\right]. \end{align} $ 图1(a)显示当形变参量(此处为
$ k_2 = 1/2000 $ )较小时, (2+1)维导数非线性薛定谔方程(56)的暗(灰)孤子解, 此时暗孤子解(61)式相对于孤子中心几乎是对称的. 图1(b)显示了当形变参量(此处为$ k_2 = 1 $ )比较大时, (2+1)维导数非线性薛定谔方程(56)的暗(灰)孤子解(61)式, 此时暗孤子解相对于孤子中心是明显不对称的. 图1(c)给出的是当$ c = 0 $ 时由(61)式表示的暗尖峰孤子结构.
图 1 导数非线性薛定谔方程(56)的单孤子解((61)式) (a) 参数取值为
$ b = 20, \ c = 1, \ k_2 = 1/2000, \ k_1 = 2, \ a = 1, \ X_0 = 0 $ ; (b) 参数取值为$ b = 20, \ c = 1, \ k_2 = 1, \ k_1 = 2, \ a = 1, \ X_0 = 1.563 $ ; (c) 由(61)式和$ c = 0 $ 表示的暗尖峰孤子结构, 其他参数与图(b)相同Figure 1. Single soliton solution (Eq. (61)) of the nonlinear Schrödinger equation (56): (a) Parameters are selected as
$b = 20, $ $ \ c = 1, \ k_2 = 1/2000, \ k_1 = 2, \ a = 1, \ X_0 = 0$ ; (b) parameters are selected as$b = 20, \ c = 1, \ k_2 = 1, \ k_1 = 2, $ $ \ a = 1, \ X_0 = 1.563$ ; (c) a dark peakon soliton solution expressed by Eq. (61) with$ c = 0 $ and other parameters are same as in panel (b) -
本文将形变术应用到了著名的(1+1)维KN系统, 得到了许多新型的互反型(D+1)维可积KN系统. 其中包括3个新的(1+1)维KN系统的互反模型、6个(2+1)维互反型可积KN系统、4个(3+1)维互反型可积KN系统和一个(4+1)维互反型可积KN系统. 6个(2+1)维模型中, 3个是原KN系统和3个不同类型互反系统的可积组合; 另3个是3个不同类型的互反系统的两两可积组合. 4个(3+1)维系统中, 3个是原KN系统和其他2个不同互反系统的可积组合, 一个是3个不同互反系统的可积组合. (4+1)维互反型KN系统包含了所有14个低维系统的可积约化. (2+1)维互反型可积KN系统(45)式允许一个互反型导数非线性薛定谔可积约化(56)式. (56)式的包络行波解可用一个复杂的椭圆积分表示. 包络暗(灰)孤子在比较小的形变下仍具有近似的中心对称形式, 但在大的形变影响下, 包络暗(灰)孤子具有明显的中心对称破缺. 包络暗孤子是一种新型的暗尖峰孤子.
从本文的结果可知, 高维可积系统是存在的, 而且非常丰富, 利用低维可积系统的不同守恒律, 可以得到很多不同类型的高维可积系统. 这类可积系统和形变前的可积系统的可积性除了Painlevé可积性难于保持外, 其他可积性, 如Lax可积性和对称可积性可以得到很好的保持. 形变系统的Lax对可以直接从形变前的Lax对应用形变术来得到. 形变系统的高阶对称不能从原系统直接形变得到, 但可以从原系统的高阶流方程的形变得到.
虽然传统的可积系统已经有很多的有效研究方法来得到严格解, 然而, 新的系统是一种全新的可积系统, 传统的求解方法已经不能再应用, 所有的研究方法需要重新研究发展. 过去对于原方程的互反方程的研究要利用互反变换变回到原方程来研究, 然后再互反回来. 但是对于现在得到的新模型, 这一有效方法不再适用, 因为原模型和互反模型被结合在了同一个模型. 大大增加了这类模型研究难度, 但也提供了新的研究机遇. 虽然形变猜想(或定理)适用于所有可积系统, 但每个可积系统各有特色, 仍然需要分别深入研究, 以期在某个合适的模型首先得到对这类模型研究的突破.
感谢胡星标教授、刘青平教授和张大军教授等提供有益的讨论.
-
可积系统研究是物理和数学等学科的重要研究课题. 然而, 通常的可积系统研究往往被限制在(1+1)维和(2+1)维, 其原因是高维可积系统极其稀少. 最近, 我们发现利用形变术可以从低维可积系统导出大量的高维可积系统. 本文利用形变术, 将(1+1)维的Kaup-Newell (KN)系统推广到(4+1)维系统. 新系统除了包含原来的(1+1)维的KN系统外, 还包含三种(1+1)维KN系统的互反形式. 模型也包含了许多新的(D+1)维(
$ D\leqslant3 $ )的互反型可积系统. (4+1)维互反型KN系统的Lax可积性和对称可积性也被证明. 新的互反型高维KN系统的求解非常困难. 本文仅研究(2+1)维互反型导数非线性薛定谔方程的行波解, 并给出薛定谔方程孤子解的隐函数表达式.-
关键词:
- 高维可积模型 /
- Kaup-Newell系统 /
- 形变术 /
- 行波解
The study of integrable systems is one of important topics both in physics and in mathematics. However, traditional studies on integrable systems are usually restricted in (1+1) and (2+1) dimensions. The main reasons come from the fact that high-dimensional integrable systems are extremely rare. Recently, we found that a large number of high dimensional integrable systems can be derived from low dimensional ones by means of a deformation algorithm. In this paper, the (1+1) dimensional Kaup-Newell (KN) system is extended to a (4+1) dimensional system with the help of the deformation algorithm. In addition to the original (1+1) dimensional KN system, the new system also contains three reciprocal forms of the (1+1) dimensional KN system. The model also contains a large number of new (D+1) dimensional ($D \leqslant 3$ ) integrable systems. The Lax integrability and symmetry integrability of the (4+1) dimensional KN system are also proved. It is very difficult to solve the new high-dimensional KN systems. In this paper, we only investigate the traveling wave solutions of a (2+1) dimensional reciprocal derivative nonlinear Schrödinger equation. The general envelope travelling wave can be expressed by a complicated elliptic integral. The single envelope dark (gray) soliton of the derivative nonlinear Schödinger equation can be implicitly written.-
Keywords:
- higher dimensional integrable models /
- Kaup-Newell systems /
- deformation algorithm /
- travelling wave solutions
[1] Gardner C S, Greene J M, Kruskal M D, Miura R M 1967 Phys. Rev. Lett. 19 1095
Google Scholar
[2] Miura R M 1968 J. Math. Phys. 9 1022
[3] Olver P J 1993 Applications of Lie Groups to Differential Equations (2nd Ed.) (New York: Springer)
[4] Lou S Y 1993 Phys. Rev. Lett. 71 4099
Google Scholar
[5] Lou S Y, Hu X B, Liu Q P 2021 JHEP 07 058
Google Scholar
[6] Ramani A, Gramaticos B, Bountis T 1989 Phys. Rep. 180 159
Google Scholar
[7] Conte R 1989 Phys. Lett. A 140 383
Google Scholar
[8] Lou S Y 1998 Z. Naturforsch 53a 251
[9] 楼森岳 1998 物理学报 47 1937
Google Scholar
Lou S Y 1998 Acta Phys. Sin. 47 1937
Google Scholar
[10] Lou S Y 1998 Phys. Rev. Lett. 80 5027
Google Scholar
[11] Hirota R 1971 Phys. Rev. Lett. 27 1192
Google Scholar
[12] Rogers C, Schief W K 2002 Backlund and Darboux Transformations, Geometry and Modern Applications in Soliton Theory (Cambridge: Cambridge University Press)
[13] Liu Q P, Mañas M 2000 Phys. Lett. B 485 293
Google Scholar
[14] Hao X Z, Lou S Y 2022 Math. Meth. Appl. Sci. 45 5774
Google Scholar
[15] Lou S Y 1993 Phys. Lett. B 302 261
Google Scholar
[16] Nijhoff F W, Sun Y Y, Zhang D J 2023 Commun. Math. Phys. 399 599
Google Scholar
[17] Zhang D J, Zhao S L 2013 Stud. Appl. Math. 131 72
Google Scholar
[18] Liu Q P, Hu X B 2005 J. Phys. A 38 6371
Google Scholar
[19] Gao X N, Lou S Y, Tang X Y 2013 JHEP 05 029
Google Scholar
[20] Xia S Q, Kaltsas D, Song D H, et al. 2021 Science 372 72
Google Scholar
[21] Loutsenko I, Roubtsov D 1997 Phys. Rev. Lett. 78 3011
Google Scholar
[22] Weigel H, Gamberg L, Reinhardt H 1997 Phys. Rev. D 55 6910
Google Scholar
[23] Dolan L 1997 Nucl. Phys. B 489 245
Google Scholar
[24] Chiueh T, Woo T P 1997 Phys. Rev. E 55 1048
Google Scholar
[25] Tajiri M, Maesono H 1997 Phys. Rev. E 55 3351
[26] Chang D E, Vuletic V, Lukin M D 2014 Nat. Photonics 8 685
Google Scholar
[27] Das G C 1997 Phys. Plasmas 4 2095
Google Scholar
[28] Jia M, Lou S Y 2006 Phy. Lett. A 353 407
Google Scholar
[29] Hu H C, Lou S Y, Chow K W 2007 Chaos, Solitons and Fractals 31 1213
Google Scholar
[30] Lou S Y 1997 J. Phys. A: Math. Phys. 30 7259
Google Scholar
[31] Lou S Y, Hao X Z, Jia M 2023 JHEP 03 018
[32] Kaup D J, Newell A C 1978 J. Math. Phys. 19 798
Google Scholar
-
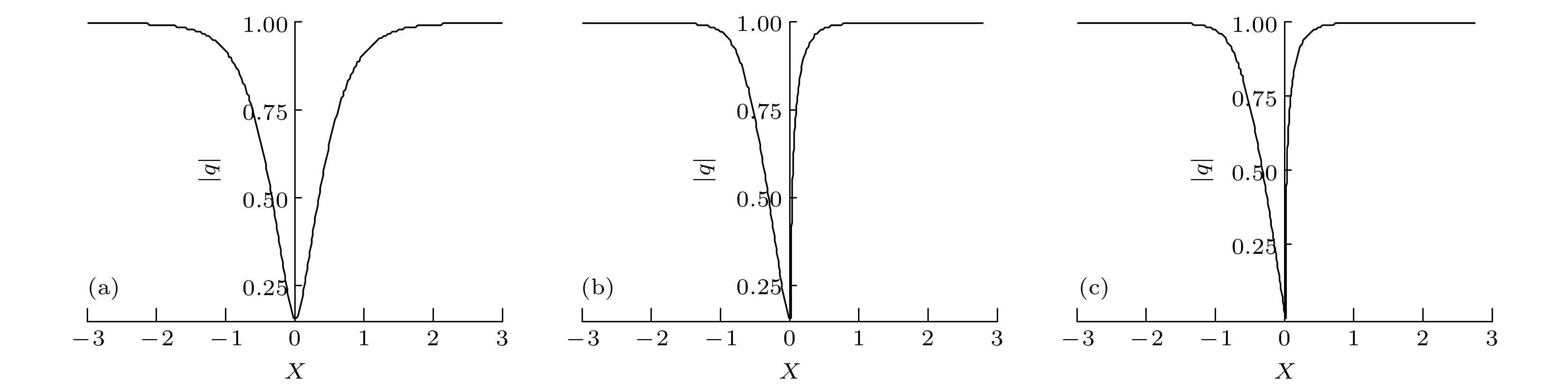
图 1 导数非线性薛定谔方程(56)的单孤子解((61)式) (a) 参数取值为
$ b = 20, \ c = 1, \ k_2 = 1/2000, \ k_1 = 2, \ a = 1, \ X_0 = 0 $ ; (b) 参数取值为$ b = 20, \ c = 1, \ k_2 = 1, \ k_1 = 2, \ a = 1, \ X_0 = 1.563 $ ; (c) 由(61)式和$ c = 0 $ 表示的暗尖峰孤子结构, 其他参数与图(b)相同Fig. 1. Single soliton solution (Eq. (61)) of the nonlinear Schrödinger equation (56): (a) Parameters are selected as
$b = 20, $ $ \ c = 1, \ k_2 = 1/2000, \ k_1 = 2, \ a = 1, \ X_0 = 0$ ; (b) parameters are selected as$b = 20, \ c = 1, \ k_2 = 1, \ k_1 = 2, $ $ \ a = 1, \ X_0 = 1.563$ ; (c) a dark peakon soliton solution expressed by Eq. (61) with$ c = 0 $ and other parameters are same as in panel (b) -
[1] Gardner C S, Greene J M, Kruskal M D, Miura R M 1967 Phys. Rev. Lett. 19 1095
Google Scholar
[2] Miura R M 1968 J. Math. Phys. 9 1022
[3] Olver P J 1993 Applications of Lie Groups to Differential Equations (2nd Ed.) (New York: Springer)
[4] Lou S Y 1993 Phys. Rev. Lett. 71 4099
Google Scholar
[5] Lou S Y, Hu X B, Liu Q P 2021 JHEP 07 058
Google Scholar
[6] Ramani A, Gramaticos B, Bountis T 1989 Phys. Rep. 180 159
Google Scholar
[7] Conte R 1989 Phys. Lett. A 140 383
Google Scholar
[8] Lou S Y 1998 Z. Naturforsch 53a 251
[9] 楼森岳 1998 物理学报 47 1937
Google Scholar
Lou S Y 1998 Acta Phys. Sin. 47 1937
Google Scholar
[10] Lou S Y 1998 Phys. Rev. Lett. 80 5027
Google Scholar
[11] Hirota R 1971 Phys. Rev. Lett. 27 1192
Google Scholar
[12] Rogers C, Schief W K 2002 Backlund and Darboux Transformations, Geometry and Modern Applications in Soliton Theory (Cambridge: Cambridge University Press)
[13] Liu Q P, Mañas M 2000 Phys. Lett. B 485 293
Google Scholar
[14] Hao X Z, Lou S Y 2022 Math. Meth. Appl. Sci. 45 5774
Google Scholar
[15] Lou S Y 1993 Phys. Lett. B 302 261
Google Scholar
[16] Nijhoff F W, Sun Y Y, Zhang D J 2023 Commun. Math. Phys. 399 599
Google Scholar
[17] Zhang D J, Zhao S L 2013 Stud. Appl. Math. 131 72
Google Scholar
[18] Liu Q P, Hu X B 2005 J. Phys. A 38 6371
Google Scholar
[19] Gao X N, Lou S Y, Tang X Y 2013 JHEP 05 029
Google Scholar
[20] Xia S Q, Kaltsas D, Song D H, et al. 2021 Science 372 72
Google Scholar
[21] Loutsenko I, Roubtsov D 1997 Phys. Rev. Lett. 78 3011
Google Scholar
[22] Weigel H, Gamberg L, Reinhardt H 1997 Phys. Rev. D 55 6910
Google Scholar
[23] Dolan L 1997 Nucl. Phys. B 489 245
Google Scholar
[24] Chiueh T, Woo T P 1997 Phys. Rev. E 55 1048
Google Scholar
[25] Tajiri M, Maesono H 1997 Phys. Rev. E 55 3351
[26] Chang D E, Vuletic V, Lukin M D 2014 Nat. Photonics 8 685
Google Scholar
[27] Das G C 1997 Phys. Plasmas 4 2095
Google Scholar
[28] Jia M, Lou S Y 2006 Phy. Lett. A 353 407
Google Scholar
[29] Hu H C, Lou S Y, Chow K W 2007 Chaos, Solitons and Fractals 31 1213
Google Scholar
[30] Lou S Y 1997 J. Phys. A: Math. Phys. 30 7259
Google Scholar
[31] Lou S Y, Hao X Z, Jia M 2023 JHEP 03 018
[32] Kaup D J, Newell A C 1978 J. Math. Phys. 19 798
Google Scholar
计量
- 文章访问数: 392
- PDF下载量: 15
- 被引次数: 0
