-
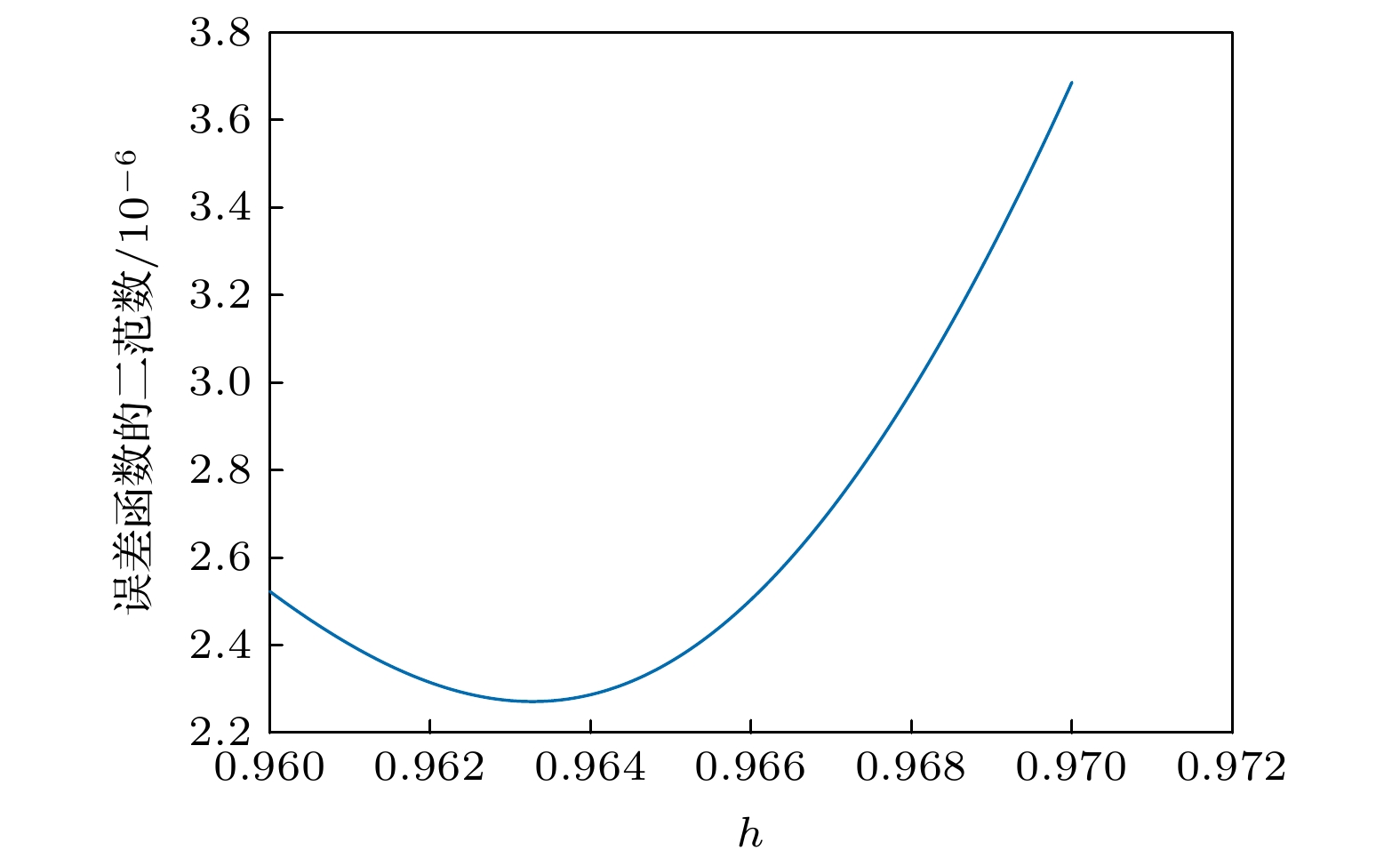
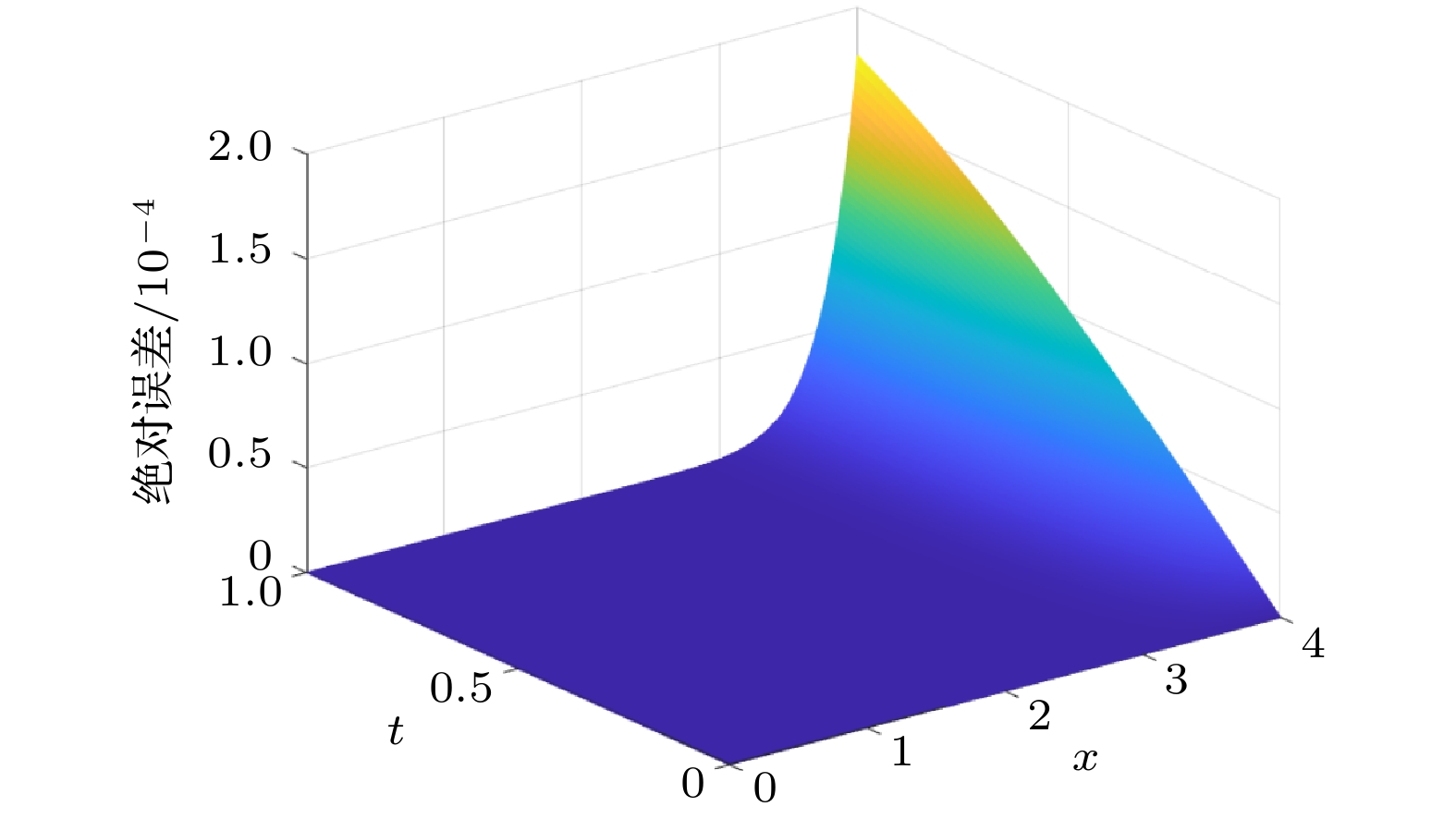
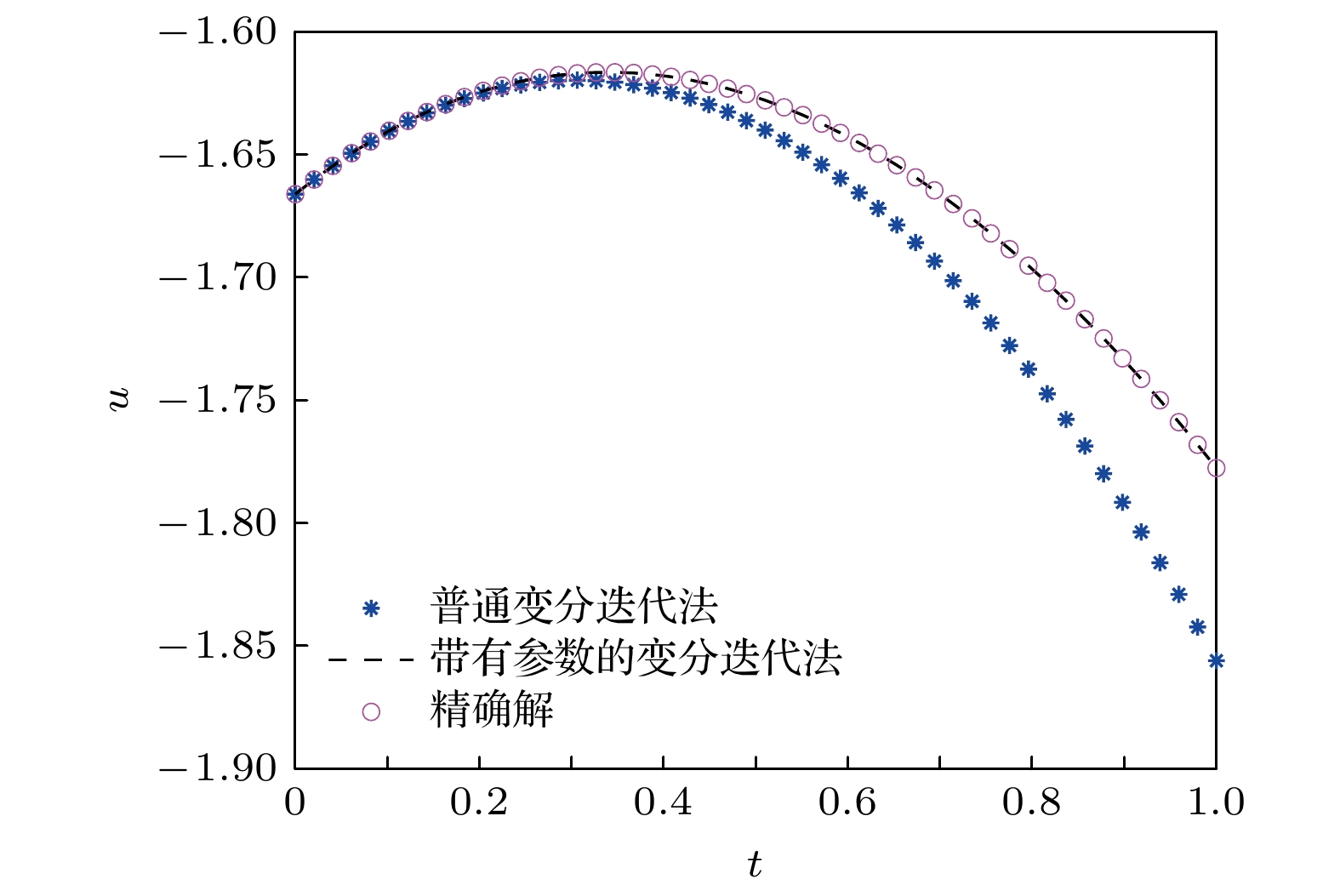
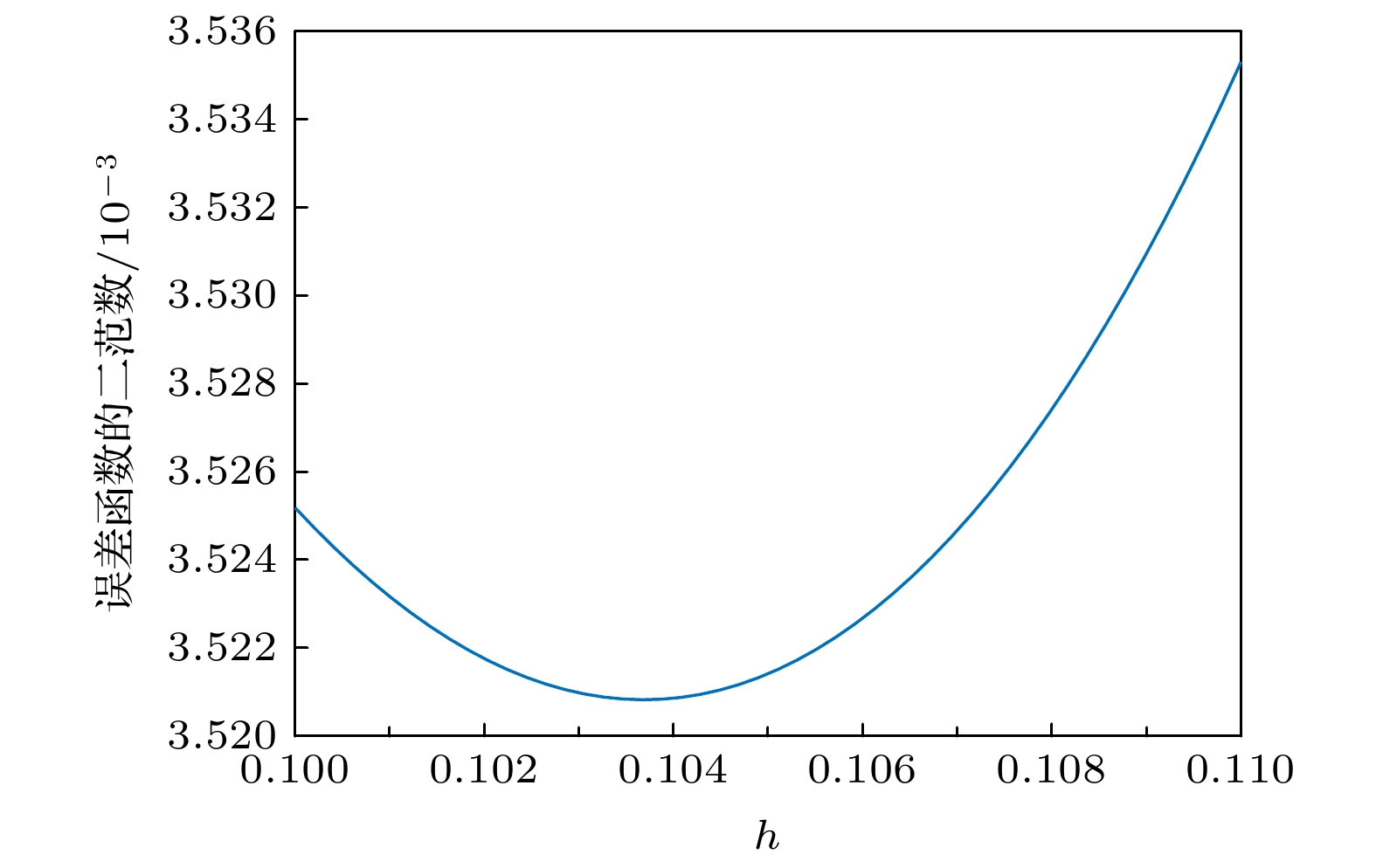
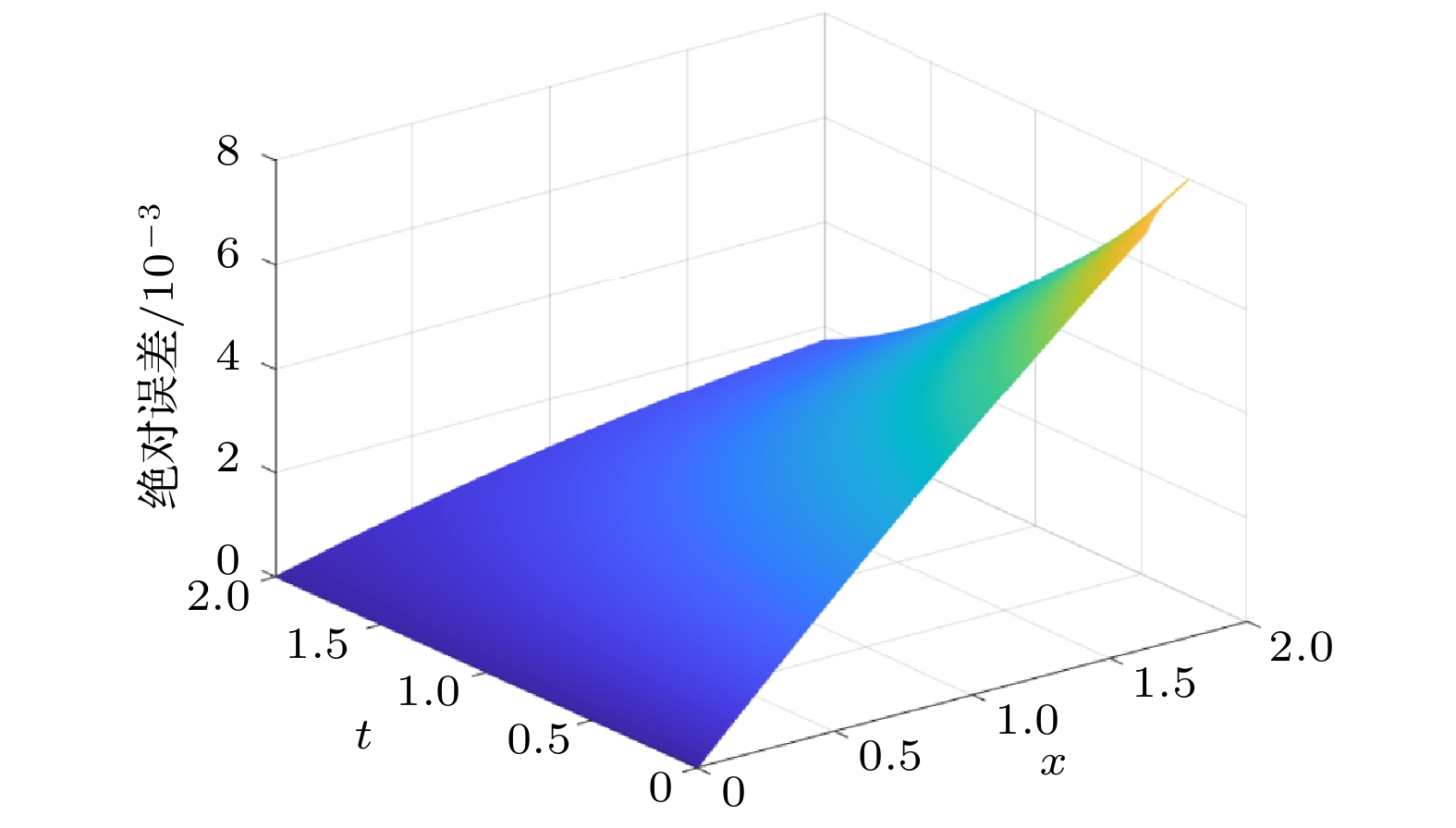
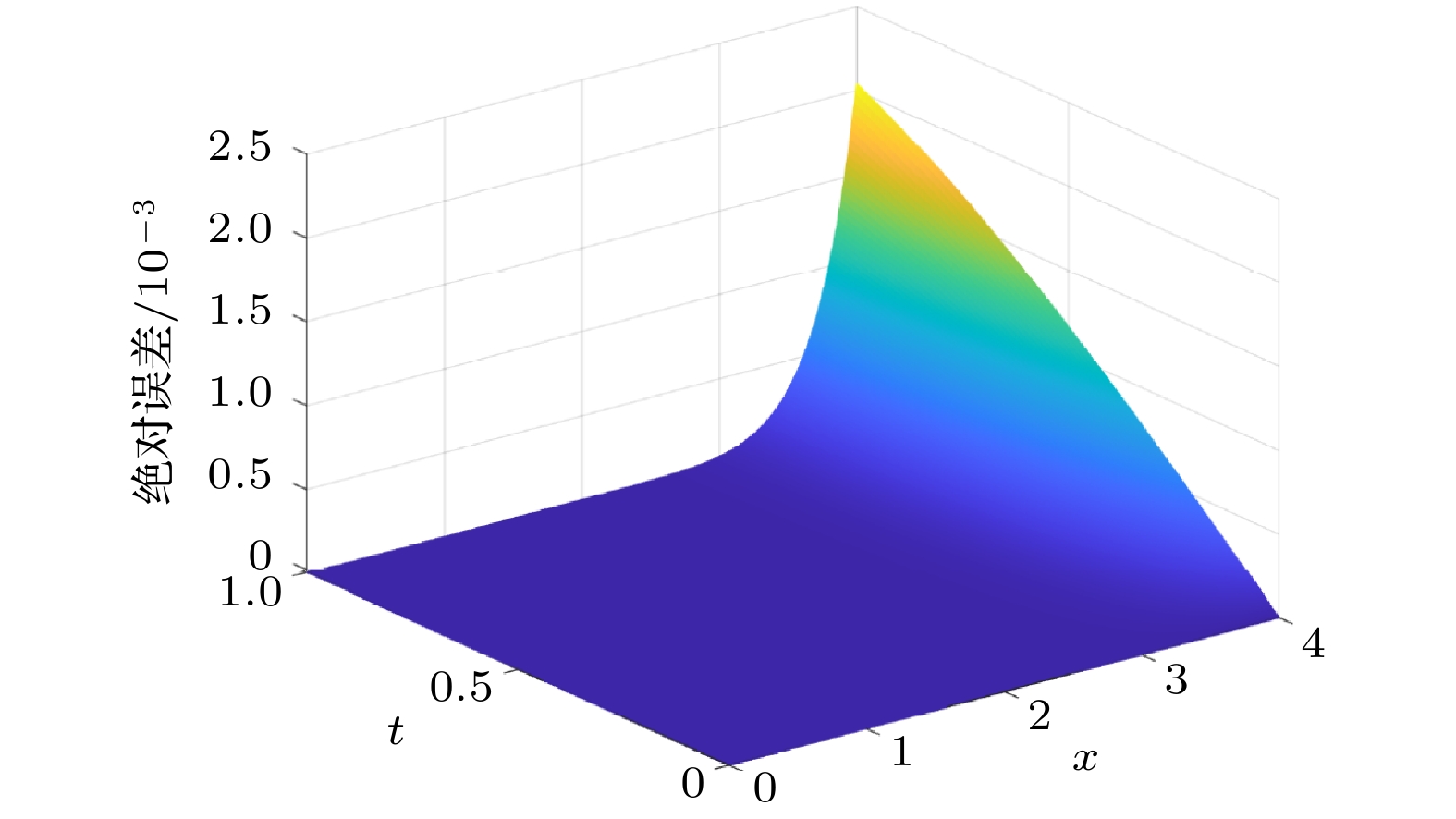
变分迭代法是一种基于变分原理, 具有高数值精度的数值格式, 目前已广泛应用于各类强非线性孤立波方程的数值求解中. 本文利用修正的变分迭代法对两类非线性方程进行研究. 该格式是对原数值方法的一种改进, 即在变分项前引入了参数h. 通过定义误差函数的离散二范数并在定义域内绘出h-曲线, 从而确定出使误差达到最小的h, 再返回原迭代过程进行求解. 同时, 参数的引入也扩大了原数值解的收敛域, 在迭代次数一定的情况下达到了数值最优. 在数值实验中, 将上述结果应用于四阶的Cahn-Hilliard方程和Benjamin-Bona-Mahoney-Burgers方程. 对于四阶的Cahn-Hilliard方程, 普通的变分迭代法绝对误差在
$10^{-1}$ 左右, 经过修正后, 绝对误差降为$10^{-4}$ , 而且修正后的方法扩大了原数值解的收敛域. 对于Benjamin-Bona-Mahony-Burgers方程, 利用带有辅助参数的变分迭代法将数值解的精度提高到$10^{-3}$ , 对真解的逼近效果优于原始的变分迭代法. 此数值方法也为其他强非线性孤立波微分方程的数值求解提供了方法和参考.The variational iteration method, based on the variational principle, is a numerical format with high numerical accuracy and convenience, has been widely applied in the numerical solution of various strong-nonlinear solitary wave equations. In this paper, the modified variational iteration method is used to improve the original numerical method, that is, the parameter h is introduced before the variational item. By defining the discrete two norm of the error function and drawing the h-curve in the domain of definition, the h that minimizes the error is determined and then returned to the original iteration process for solution. In this paper, We choose the uniform grid points to caculate the error. At the same time, the introduction of parameters also expands the convergence domain of the original numerical solution and achieves the numerical optimization under the condition of a certain number of iterations, which shows better than the general method. In the numerical experiment, the above results are applied to the fourth-order Cahn-Hilliard equation and the Benjamin-Bona-Mahony-Burgers equation. The Cahn-Hilliard equation was first found to describe the phenomeno in interface dynamics. It has vital application in physical. For the fourth-order Cahn-Hilliard equation, the error order of the ordinary variational iteration method is about$10^{-1}$ , and the absolute error is reduced to$10^{-4}$ after the modification. Moreover, the modified method expands the convergence domain of the original numerical solution. And the Benjamin-Bona-Mahony-Burgers equation can be degenerated to the Benjamin-Bona-Mahony and the Burgers equation under the appropriate parameter selection. For the Benjamin-Bona-Mahony-Burgers equation, if using the normal method, we can find that the numerical solution will not converge. But the accuracy of the numerical solution is decreased to$10^{-3}$ by using the variational iteration method with auxiliary parameters, which is superior to the original variational iteration method in the approximation effect of the true solution. This numerical method also provides a scheme and reference for the numerical solution of other strong-nonlinear solitary wave differential equations. This scheme provieds a continuous solution in the time and space domain, which differs from the finite difference method, finite volume scheme and so on. That means we can use this method independently without using any other scheme to match our approarch, this is also the advantage of the modified variational iteration method.-
Keywords:
- modified variational iteration method /
- nonlinear solitary wave equation /
- fourth order Cahn-Hilliard equation /
- Benjamin-Bona-Mahony-Burgers equation
[1] Kartashov Y V, Astrakharchik G E, Malomed B A, Torner L 2019 Nat. Rev. Phys. 1 185
 Google Scholar
Google Scholar
[2] Kengne E, Liu W M, Malomed B A 2020 Phys. Rep. 1 899
[3] 张大军 2020 物理学报 69 010202
 Google Scholar
Google Scholar
Zhang D J 2020 Acta Phys. Sin. 69 010202
 Google Scholar
Google Scholar
[4] 宋彩芹, 朱佐农 2020 物理学报 69 010204
 Google Scholar
Google Scholar
Song C Q, Zhu Z N 2020 Acta Phys. Sin. 69 010204
 Google Scholar
Google Scholar
[5] Wang P, Zheng Y L, Chen X F, Huang C M, Kartashov Y V, Torner L, Konotop, V V, Ye F W 2020 Nature 577 42
 Google Scholar
Google Scholar
[6] Fu Q D, Wang P, Huang C M, Kartashov Y V, Torner L, Konotop V V, Ye F W 2020 Nat. Photonics 14 663
 Google Scholar
Google Scholar
[7] Tian S F 2016 Proc. Math. Phys. Eng. Sci. 472 20160588
 Google Scholar
Google Scholar
[8] Tian S F 2017 J. Differ. Equ. 262 506
 Google Scholar
Google Scholar
[9] Ma W X 2020 Appl. Math. Lett. 102 106161
 Google Scholar
Google Scholar
[10] Zhang G Q, Yan Z Y 2020 Physica D 402 132170
 Google Scholar
Google Scholar
[11] Wang X B, Han B 2020 J. Math. Anal. Appl. 487 123968
 Google Scholar
Google Scholar
[12] Li B Q, Ma Y L 2020 Appl. Math. Comput. 386 125469
 Google Scholar
Google Scholar
[13] Su J J, Gao Y T, Ding C C 2019 Appl. Math. Lett. 88 201
 Google Scholar
Google Scholar
[14] Zhang X, Wang R, Zhang Y Q, Kartashov Y V, Li F, Zhong H, Guan H, Gao K, Li F, Zhang Y P, Xiao M 2020 Nat. Commun. 11 1902
 Google Scholar
Google Scholar
[15] Jin K, Li Y, Li F, Belic M R, Zhang Y P, Zhang Y Q 2020 Adv. Photonics 2 046002
 Google Scholar
Google Scholar
[16] Zeng L, Zeng J 2019 Adv. Photonics. 1 046004
 Google Scholar
Google Scholar
[17] Zeng L, Zeng J 2020 Commun. Phys. 3 26
 Google Scholar
Google Scholar
[18] Yang J K 2008 J. Comput. Phys. 227 6862
 Google Scholar
Google Scholar
[19] Bao W Z, Yin J 2019 Res. Math. Sci. 6 1
 Google Scholar
Google Scholar
[20] Antoine X, Bao W Z, Besse C 2013 Comput. Phys. Commun. 184 2621
 Google Scholar
Google Scholar
[21] Cockburn B, Shu C W 1998 SIAM J. Math. Anal. 35 2440
 Google Scholar
Google Scholar
[22] Jiang G S, Shu C W 1996 J. Comput. Phys. 126 202
 Google Scholar
Google Scholar
[23] He J H 1999 Int. J. Non. Linear Mech. 34 699
 Google Scholar
Google Scholar
[24] He J H 2007 J. Comput. Appl. Math. 207 3
 Google Scholar
Google Scholar
[25] He J H 2007 Comput. Math. Appl. 54 881
 Google Scholar
Google Scholar
[26] Hesameddini E, Latifizadeh H 2009 J. Nonlinear Sci. Numer. Simul. 10 1377
 Google Scholar
Google Scholar
[27] Salkuyeh D K 2008 Comput. Math. Appl. 56 2027
 Google Scholar
Google Scholar
[28] Noor M A, Mohyud-Din S T 2008 J. Nonlinear Sci. Numer. Simul. 9 141
 Google Scholar
Google Scholar
[29] Liao S J 2004 Appl. Math. Comput. 147 499
 Google Scholar
Google Scholar
[30] Zayed E M, Rahman H 2009 J. Nonlinear Sci. Numer. Simul. 10 1093
 Google Scholar
Google Scholar
[31] Hosseini M M, Mohyud-Din S T, Ghaneai H, Usman M 2010 J. Comput. Appl. Math. 11 495
 Google Scholar
Google Scholar
[32] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
 Google Scholar
Google Scholar
[33] Barrett J W, Blowey J F 1997 Numer. Math. 77 1
 Google Scholar
Google Scholar
[34] Wells G N, Kuhl E, Garikipati K 2006 J. Comput. Phys. 218 860
 Google Scholar
Google Scholar
[35] Kay D, Welford R 2006 J. Comput. Phys. 212 288
 Google Scholar
Google Scholar
[36] Benjamin T B, Bona J L, Mahony J J 1972 Philos. Trans. R. Soc. A 272 47
 Google Scholar
Google Scholar
[37] Karakoc S B G, Bhowmik S K 2019 Comput. Math. Appl. 77 1917
 Google Scholar
Google Scholar
-
表 1 不同点处真解与数值解对比
Table 1. Comparison of true and numerical solutions at different points
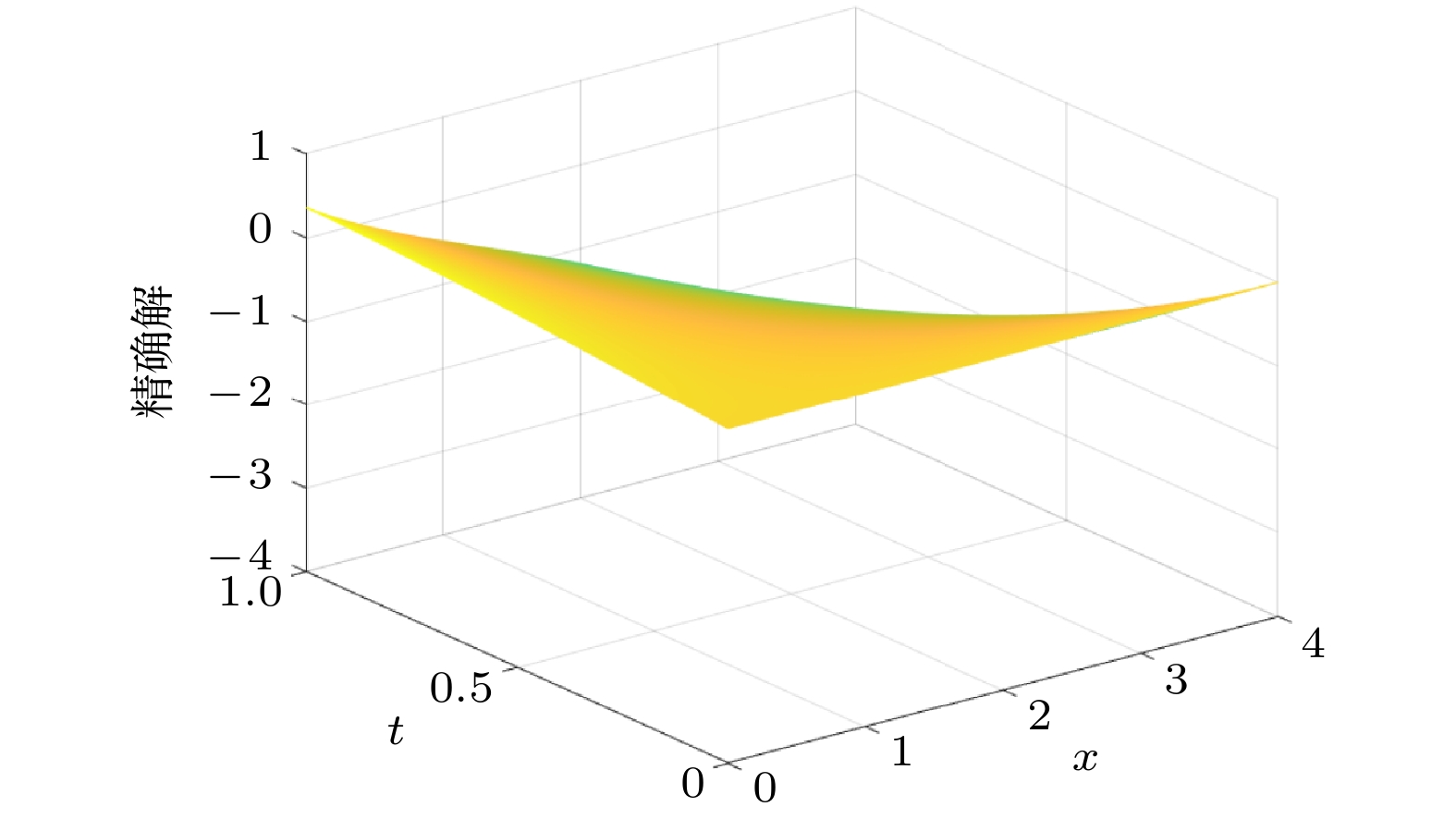
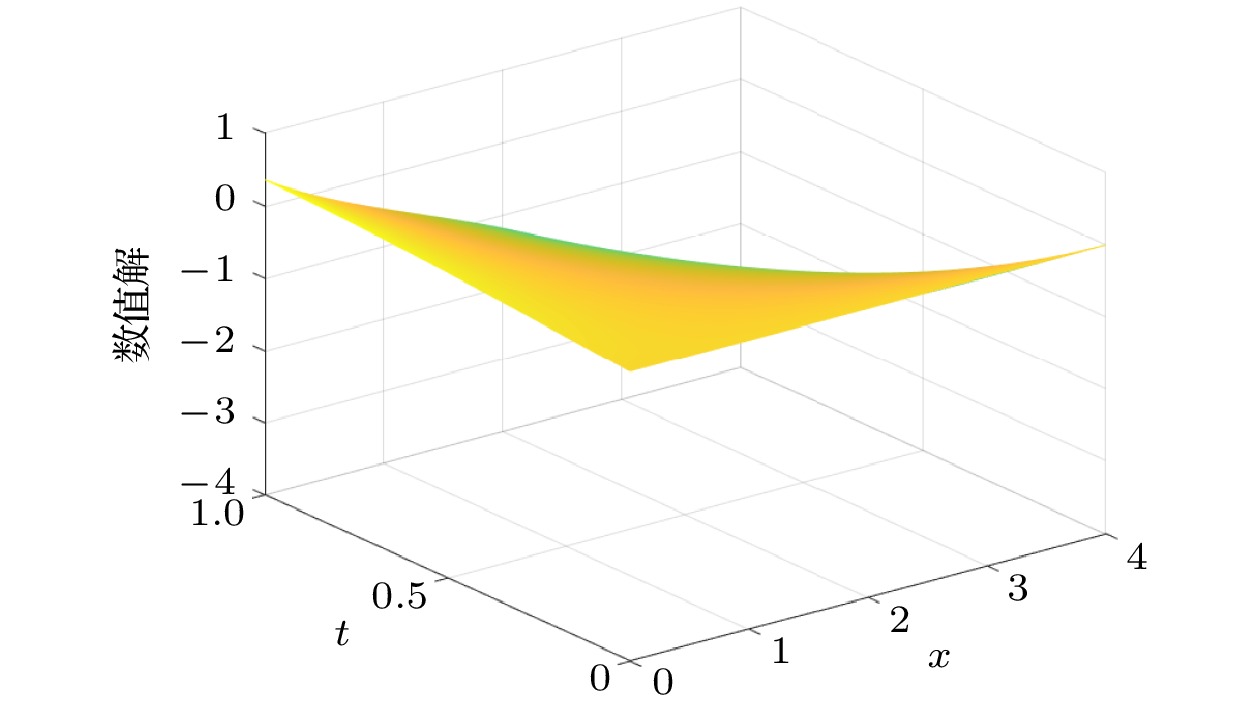
$ (x, t)$ 原始数值解$ u_1$ 修正数值解$ u_2$ 精确解u (1, 0.2) –1.855 × 10–1 –1.855 × 10–1 –1.855 × 10–1 (1, 0.4) –2.176 × 10–1 –1.857 × 10–1 –1.864 × 10–1 (1, 0.6) –2.970 × 10–1 –1.860 × 10–1 –1.873 × 10–1 (1, 0.8) –4.234 × 10–1 –1.862 × 10–1 –1.881 × 10–1 (1, 1.0) –6.297 × 10–1 –1.863 × 10–1 –1.889 × 10–1 (1, 1.2) –8.914 × 10–1 –1.866 × 10–1 –1.893 × 10–1 (1, 1.4) –1.212 –1.868 × 10–1 –1.903 × 10–1 (1, 1.6) –1.590 –1.870 × 10–1 –1.910 × 10–1 (1, 1.8) –2.033 –1.872 × 10–1 –1.916 × 10–1 (1, 2.0) –2.429 –1.874 × 10–1 –1.922 × 10–1 -
[1] Kartashov Y V, Astrakharchik G E, Malomed B A, Torner L 2019 Nat. Rev. Phys. 1 185
 Google Scholar
Google Scholar
[2] Kengne E, Liu W M, Malomed B A 2020 Phys. Rep. 1 899
[3] 张大军 2020 物理学报 69 010202
 Google Scholar
Google Scholar
Zhang D J 2020 Acta Phys. Sin. 69 010202
 Google Scholar
Google Scholar
[4] 宋彩芹, 朱佐农 2020 物理学报 69 010204
 Google Scholar
Google Scholar
Song C Q, Zhu Z N 2020 Acta Phys. Sin. 69 010204
 Google Scholar
Google Scholar
[5] Wang P, Zheng Y L, Chen X F, Huang C M, Kartashov Y V, Torner L, Konotop, V V, Ye F W 2020 Nature 577 42
 Google Scholar
Google Scholar
[6] Fu Q D, Wang P, Huang C M, Kartashov Y V, Torner L, Konotop V V, Ye F W 2020 Nat. Photonics 14 663
 Google Scholar
Google Scholar
[7] Tian S F 2016 Proc. Math. Phys. Eng. Sci. 472 20160588
 Google Scholar
Google Scholar
[8] Tian S F 2017 J. Differ. Equ. 262 506
 Google Scholar
Google Scholar
[9] Ma W X 2020 Appl. Math. Lett. 102 106161
 Google Scholar
Google Scholar
[10] Zhang G Q, Yan Z Y 2020 Physica D 402 132170
 Google Scholar
Google Scholar
[11] Wang X B, Han B 2020 J. Math. Anal. Appl. 487 123968
 Google Scholar
Google Scholar
[12] Li B Q, Ma Y L 2020 Appl. Math. Comput. 386 125469
 Google Scholar
Google Scholar
[13] Su J J, Gao Y T, Ding C C 2019 Appl. Math. Lett. 88 201
 Google Scholar
Google Scholar
[14] Zhang X, Wang R, Zhang Y Q, Kartashov Y V, Li F, Zhong H, Guan H, Gao K, Li F, Zhang Y P, Xiao M 2020 Nat. Commun. 11 1902
 Google Scholar
Google Scholar
[15] Jin K, Li Y, Li F, Belic M R, Zhang Y P, Zhang Y Q 2020 Adv. Photonics 2 046002
 Google Scholar
Google Scholar
[16] Zeng L, Zeng J 2019 Adv. Photonics. 1 046004
 Google Scholar
Google Scholar
[17] Zeng L, Zeng J 2020 Commun. Phys. 3 26
 Google Scholar
Google Scholar
[18] Yang J K 2008 J. Comput. Phys. 227 6862
 Google Scholar
Google Scholar
[19] Bao W Z, Yin J 2019 Res. Math. Sci. 6 1
 Google Scholar
Google Scholar
[20] Antoine X, Bao W Z, Besse C 2013 Comput. Phys. Commun. 184 2621
 Google Scholar
Google Scholar
[21] Cockburn B, Shu C W 1998 SIAM J. Math. Anal. 35 2440
 Google Scholar
Google Scholar
[22] Jiang G S, Shu C W 1996 J. Comput. Phys. 126 202
 Google Scholar
Google Scholar
[23] He J H 1999 Int. J. Non. Linear Mech. 34 699
 Google Scholar
Google Scholar
[24] He J H 2007 J. Comput. Appl. Math. 207 3
 Google Scholar
Google Scholar
[25] He J H 2007 Comput. Math. Appl. 54 881
 Google Scholar
Google Scholar
[26] Hesameddini E, Latifizadeh H 2009 J. Nonlinear Sci. Numer. Simul. 10 1377
 Google Scholar
Google Scholar
[27] Salkuyeh D K 2008 Comput. Math. Appl. 56 2027
 Google Scholar
Google Scholar
[28] Noor M A, Mohyud-Din S T 2008 J. Nonlinear Sci. Numer. Simul. 9 141
 Google Scholar
Google Scholar
[29] Liao S J 2004 Appl. Math. Comput. 147 499
 Google Scholar
Google Scholar
[30] Zayed E M, Rahman H 2009 J. Nonlinear Sci. Numer. Simul. 10 1093
 Google Scholar
Google Scholar
[31] Hosseini M M, Mohyud-Din S T, Ghaneai H, Usman M 2010 J. Comput. Appl. Math. 11 495
 Google Scholar
Google Scholar
[32] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
 Google Scholar
Google Scholar
[33] Barrett J W, Blowey J F 1997 Numer. Math. 77 1
 Google Scholar
Google Scholar
[34] Wells G N, Kuhl E, Garikipati K 2006 J. Comput. Phys. 218 860
 Google Scholar
Google Scholar
[35] Kay D, Welford R 2006 J. Comput. Phys. 212 288
 Google Scholar
Google Scholar
[36] Benjamin T B, Bona J L, Mahony J J 1972 Philos. Trans. R. Soc. A 272 47
 Google Scholar
Google Scholar
[37] Karakoc S B G, Bhowmik S K 2019 Comput. Math. Appl. 77 1917
 Google Scholar
Google Scholar
计量
- 文章访问数: 7363
- PDF下载量: 102
- 被引次数: 0



















 下载:
下载: