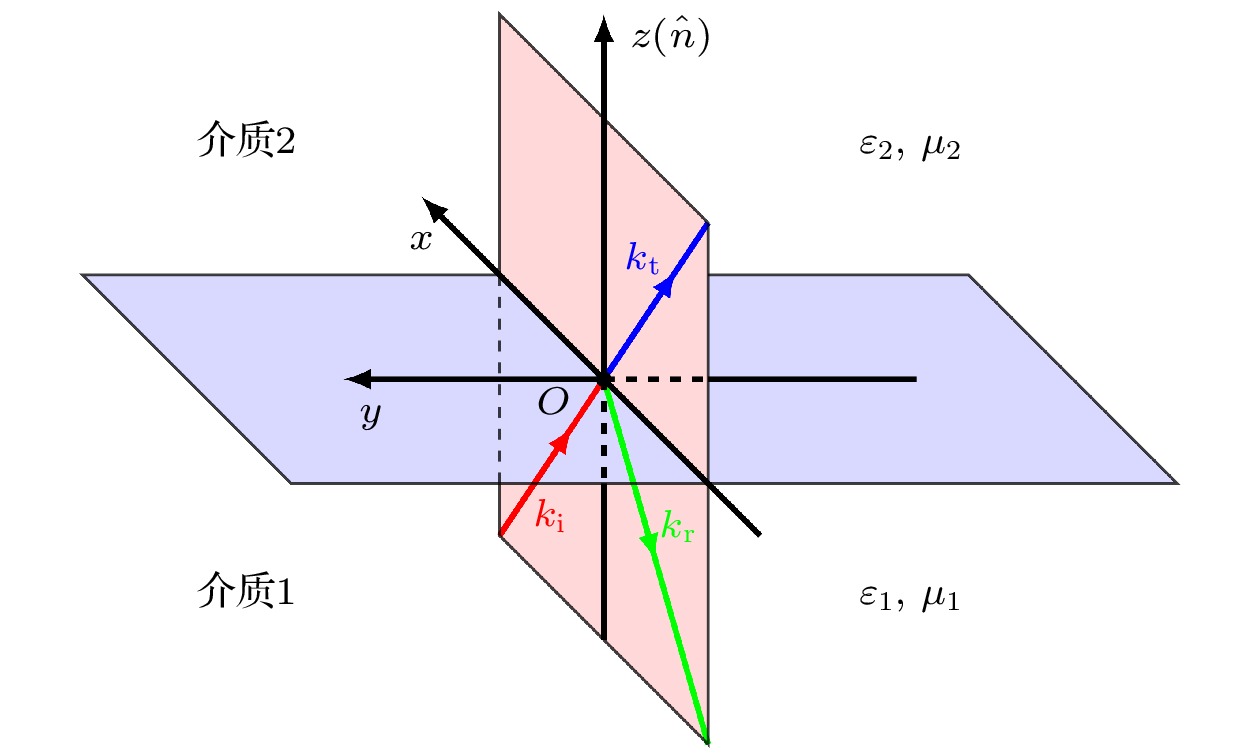
-
Due to the boundary conditions of electromagnetic fields and phase matching of electro magnetic waves on interface being the basis to drive the Snell’s laws and Fresnel’s laws, they are also crucial for the analysis of electromagnetic wave propagation in a moving medium. There are mainly two methods to derive the boundary conditions of electromagnetic fields on moving interface. One of them is to use the kinematic integral form, yet this method is based on the classical time-space, and the other is based on the relativistic transformation, the boundary conditions are derived from the scaling effect with geometric method, or from the principle of relativity directly. However, the first one has a form the same as the form obtained by using the kinematic integral form, while the second one obtains a different form. At the same time, the phase matching of electromagnetic wave on moving interface is only discussed by Galileo transformation, however this is unreasonable, because of the relativistic effect cannot be ignored here. Therefore, it is necessary to reexamine the boundary conditions of electromagnetic fields and phase matching of electromagnetic wave on moving interface. Herein, firstly, the relativistic transformation formula of the unit normal vector of moving surface is derived from the surface equation and principle of relativity. Secondly, the boundary conditions of electromagnetic fields on moving interface are given based on the relativistic transformation formula and the non-relativistic transformation formula of the unit normal vector and electromagnetic fields, which show that the boundary conditions of electromagnetic fields on moving interface under the relativistic case and the non-relativistic case have the same form. This is not accidental but definite, because the change of flux of electromagnetic fields, like the change of magnetic flux, from the induction of electromagnetic filed is the same as that from the variation of surface element. Thirdly, the phase matching of electromagnetic wave on moving interface is given based on the relativistic transformation formula of the unit normal vector and the phase matching of electromagnetic wave on resting interface. In the problem of light incident on a homogeneous medium moving at a constant velocity in vacuum or air, using the phase matching of electromagnetic wave on moving interface, the same results can be easily obtained through other methods. The discussion in this study belongs to classical electrodynamics with no quantum effects considered, but the results will provide some conveniences for theoretically analyzing electromagnetic communication, remote sensing and telemetering.
-
Keywords:
- electromagnetic wave /
- moving interface /
- phase matching /
- relativity principle
[1] Kolesnichenko Y I, Lutsenko V V, Tykhyy A V 2023 J. Plasma Phys. 89 905890401
Google Scholar
[2] Davidovich M V 2022 Tech. Phys. 67 549
Google Scholar
[3] Tsironis C, Papadopoulos A 2023 J. Electromagn. Waves Appl. 37 1366
Google Scholar
[4] Sheng X L, Li Y, Wang Q 2022 Symmetry 14 1641
Google Scholar
[5] 戴希, 沙威, 陈昊 2022 物理 51 8
Google Scholar
Dai X, Sha W, Chen H 2022 Physics 51 8
Google Scholar
[6] 王雯宇, 刘新宇, 许洋 2022 物理与工程 32 7
Wang W Y, Liu X Y, Xu Y 2022 Physics and Engineering 32 7
[7] 王青 2022 物理与工程 32 4
Google Scholar
Wang Q 2022 Physics and Engineering 32 4
Google Scholar
[8] Kong J A 1985 Electromagnetic Wave Theory (New York: John Wiley & Sons) p557
[9] Costen R C, Adamson D 1965 Proc. IEEE 53 1181
Google Scholar
[10] 陈秉乾, 舒幼生, 胡望雨 2021 电磁学专题研究 (北京: 北京大学出版社) 第429页
Chen B Q, Shu Y S, Hu W Y 2021 Monographic Study On Electromagnetics (Beijing: Peking University Press) p429
[11] 邹澎 1987 大学物理 7 22
Google Scholar
Zou P 1987 College Physics 7 22
Google Scholar
[12] 陈达章 1991 大学物理 7 19
Google Scholar
Chen D Z 1991 College Physics 7 19
Google Scholar
[13] 梁昌洪, 褚庆昕 2002 物理学报 51 2202
Google Scholar
Liang C H, Zhu Q X 2002 Acta Phys. Sin. 51 2202
Google Scholar
[14] Yuan J J, Meng G P, Gu M 2022 Nucl. Sci. Tech. 33 9
Google Scholar
[15] L iu W, Cui C, Wang X, et al. 2015 IEEE Trans. Plasma Sci. 43 405
Google Scholar
[16] 朱家柱, 刘伟, 崔驰等 2014 核技术 37 030203
Google Scholar
Zhu J Z, Liu W, Cui C, et al. 2014 Nuclear Science and Techniques 37 030203
Google Scholar
[17] Mackay T G, Akhlesh L 2020 The Transfer-matrix Method in Electromagnetics and Optics (Switzerland: Springer Nature) p33
[18] Byron F W, Fuller R W 1992 Mathematics of Classical and Quantum Physics (New York: Dover) p15
[19] Hass J, Heil C, Weir M D 2017 Thomas’ Calculus (14th Ed.) (Boston: Pearson) p792
[20] Morris C C, Stark R M 2015 Fundamentals of Calculus (New York: John Wiley & Sons) p217
[21] Lax M, Nelson D F 1976 Phys. Rev. B 13 1777
Google Scholar
-
[1] Kolesnichenko Y I, Lutsenko V V, Tykhyy A V 2023 J. Plasma Phys. 89 905890401
Google Scholar
[2] Davidovich M V 2022 Tech. Phys. 67 549
Google Scholar
[3] Tsironis C, Papadopoulos A 2023 J. Electromagn. Waves Appl. 37 1366
Google Scholar
[4] Sheng X L, Li Y, Wang Q 2022 Symmetry 14 1641
Google Scholar
[5] 戴希, 沙威, 陈昊 2022 物理 51 8
Google Scholar
Dai X, Sha W, Chen H 2022 Physics 51 8
Google Scholar
[6] 王雯宇, 刘新宇, 许洋 2022 物理与工程 32 7
Wang W Y, Liu X Y, Xu Y 2022 Physics and Engineering 32 7
[7] 王青 2022 物理与工程 32 4
Google Scholar
Wang Q 2022 Physics and Engineering 32 4
Google Scholar
[8] Kong J A 1985 Electromagnetic Wave Theory (New York: John Wiley & Sons) p557
[9] Costen R C, Adamson D 1965 Proc. IEEE 53 1181
Google Scholar
[10] 陈秉乾, 舒幼生, 胡望雨 2021 电磁学专题研究 (北京: 北京大学出版社) 第429页
Chen B Q, Shu Y S, Hu W Y 2021 Monographic Study On Electromagnetics (Beijing: Peking University Press) p429
[11] 邹澎 1987 大学物理 7 22
Google Scholar
Zou P 1987 College Physics 7 22
Google Scholar
[12] 陈达章 1991 大学物理 7 19
Google Scholar
Chen D Z 1991 College Physics 7 19
Google Scholar
[13] 梁昌洪, 褚庆昕 2002 物理学报 51 2202
Google Scholar
Liang C H, Zhu Q X 2002 Acta Phys. Sin. 51 2202
Google Scholar
[14] Yuan J J, Meng G P, Gu M 2022 Nucl. Sci. Tech. 33 9
Google Scholar
[15] L iu W, Cui C, Wang X, et al. 2015 IEEE Trans. Plasma Sci. 43 405
Google Scholar
[16] 朱家柱, 刘伟, 崔驰等 2014 核技术 37 030203
Google Scholar
Zhu J Z, Liu W, Cui C, et al. 2014 Nuclear Science and Techniques 37 030203
Google Scholar
[17] Mackay T G, Akhlesh L 2020 The Transfer-matrix Method in Electromagnetics and Optics (Switzerland: Springer Nature) p33
[18] Byron F W, Fuller R W 1992 Mathematics of Classical and Quantum Physics (New York: Dover) p15
[19] Hass J, Heil C, Weir M D 2017 Thomas’ Calculus (14th Ed.) (Boston: Pearson) p792
[20] Morris C C, Stark R M 2015 Fundamentals of Calculus (New York: John Wiley & Sons) p217
[21] Lax M, Nelson D F 1976 Phys. Rev. B 13 1777
Google Scholar
下载:
计量
- 文章访问数: 2067
- PDF下载量: 39
- 被引次数: 0
