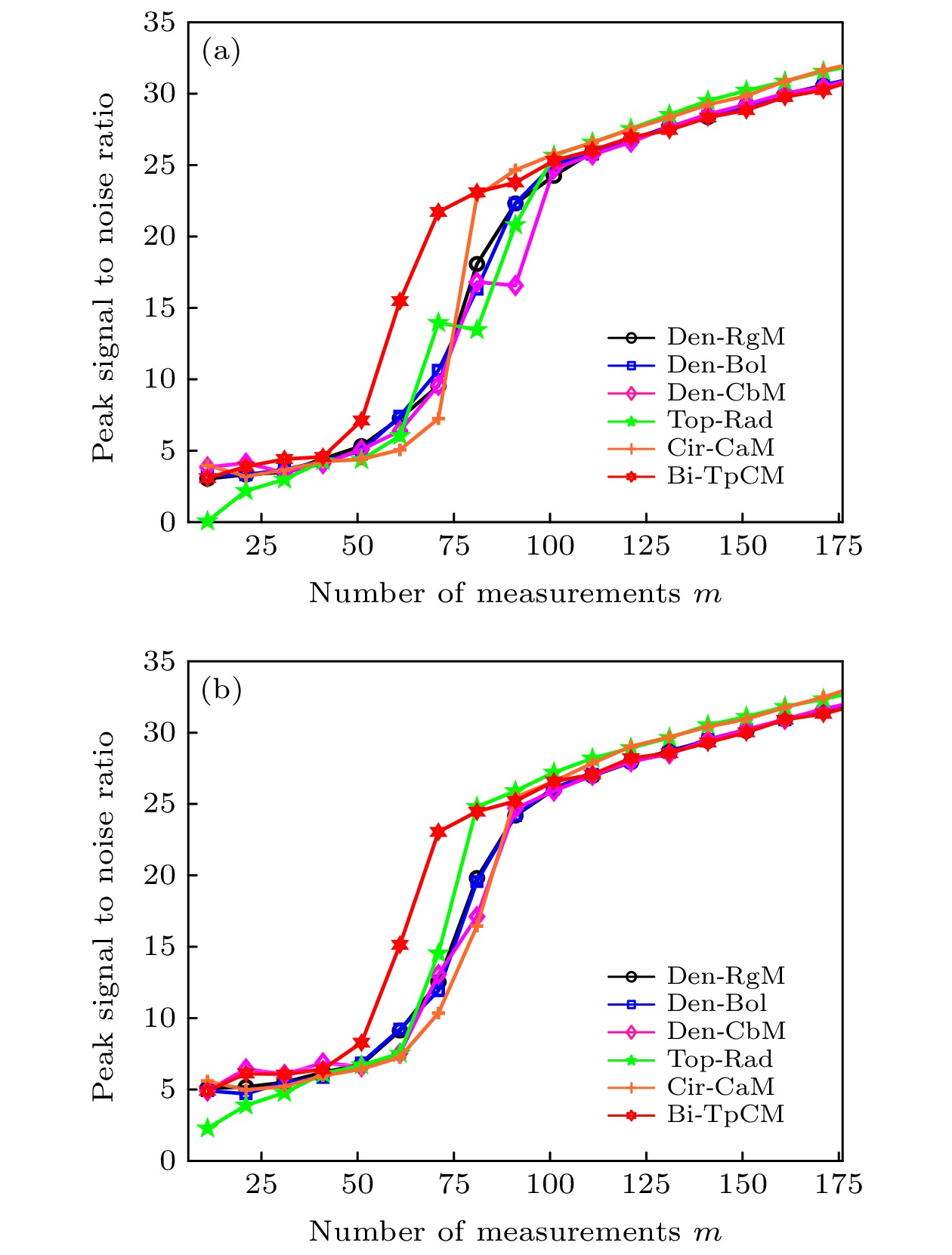
-
Compressed sensing is a revolutionary signal processing technique, which allows the signals of interest to be acquired at a sub-Nyquist rate, meanwhile still permitting the signals from highly incomplete measurements to be reconstructed perfectly. As is well known, the construction of sensing matrix is one of the key technologies to promote compressed sensing from theory to application. Because the Toeplitz sensing matrix can support fast algorithm and corresponds to discrete convolution operation, it has essential research significance. However, the conventional random Toeplitz sensing matrix, due to the uncertainty of its elements, is subject to many limitations in practical applications, such as high memory consumption and difficulty of hardware implementation. To avoid these limitations, we propose a bipolar Toeplitz block-based chaotic sensing matrix (Bi-TpCM) by combining the intrinsic advantages of Toeplitz matrix and bipolar chaotic sequence. Firstly, the generation of bipolar chaotic sequence is introduced and its statistical characteristics are analyzed, showing that the generated bipolar chaotic sequence is an independent and identically distributed Rademacher sequence, which makes it possible to construct the sensing matrix. Secondly, the proposed Bi-TpCM is constructed, and it is proved that Bi-TpCM has almost optimal theoretical guarantees in terms of the coherence, and also satisfies the restricted isometry condition. Finally, the measurement performances on one-dimensional signals and images by using the proposed Bi-TpCM are investigated and compared with those of its counterparts, including random matrix, random Toeplitz matrix, real-valued chaotic matrix, and chaotic circulant sensing matrix. The results show that Bi-TpCM not only has better performance for these testing signals, but also possesses considerable advantages in terms of the memory cost, computational complexity, and hardware realization. In particular, the proposed Bi-TpCM is extremely suitable for the compressed sensing measurement of linear time-invariant (LTI) systems with multiple inputs and single output, such as the joint parameter and time-delay estimation for finite impulse response. Moreover, the construction framework of the proposed Bi-TpCM can be extended to different chaotic systems, such as Logistic or Cat chaotic systems, and it is also possible for the proposed Bi-TpCM to derive the Hankel blocks, additional stacking of blocks, partial circulant blocks sensing matrices. With these block-based sensing architectures, we can more easily implement compressed sensing for various compressed measurement problems of LTI systems.
-
Keywords:
- compressed sensing /
- chaotic sequence /
- Toeplitz matrix /
- coherence
[1] Candès E J, Romberg J, Tao T 2006 IEEE Trans. Inf. Theory 52 1289
Google Scholar
[2] 庄佳衍, 陈钱, 何伟基, 冒添逸 2016 物理学报 65 040501
Google Scholar
Zhuang J Y, Chen Q, He W J, Mao T Y 2016 Acta Phys. Sin. 65 040501
Google Scholar
[3] Eldar Y C, Kutyniok G 2012 Compressed Sensing: Theory and Applications (Cambridge: Cambridge University Press) pp1−5
[4] 石航, 王丽丹 2019 物理学报 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[5] Hyder M M, Mahata K 2010 IEEE Trans. Signal Process. 58 2194
Google Scholar
[6] Wang J, Shim B 2012 IEEE Trans. Signal Process. 60 4973
Google Scholar
[7] Chen S S, Donoho D L, Saunders M A 2001 SIAM Review 43 129
Google Scholar
[8] Candès E J 2008 C. R. Math. 346 589
Google Scholar
[9] Donoho D L, Huo X M 2001 IEEE Trans. Inf. Theory 47 2845
Google Scholar
[10] Lu W Z, Li W Y, Zhang W, Xia S T 2018 IEEE Trans. Signal Inf. Process. Networks 5 418
Google Scholar
[11] Ansari N, Gupta A 2017 IEEE Trans. Image Process. 26 3680
Google Scholar
[12] Haupt J, Bajwa W U, Raz G, Nowak R 2010 IEEE Trans. Inf. Theory 56 5862
Google Scholar
[13] Yu L, Barbot J P, Zheng G, Sun H 2010 IEEE Signal Process. Lett. 17 731
Google Scholar
[14] Gan H P, Li Z, Li J, Wang X, Cheng Z F 2014 Nonlinear Dyn. 78 2429
Google Scholar
[15] 郭静波, 汪韧 2014 物理学报 63 198402
Google Scholar
Guo J B, Wang R 2014 Acta Phys. Sin. 63 198402
Google Scholar
[16] 郭静波, 李佳文 2015 物理学报 64 198401
Google Scholar
Guo J B, Li J W 2015 Acta Phys. Sin. 64 198401
Google Scholar
[17] 陶太洋 2016 硕士学位论文 (无锡: 江南大学)
Tao T Y 2016 M. S. Thesis (Wuxi: Jiangnan University) (in Chinese)
[18] Kohda T 2002 Proc. IEEE 90 641
Google Scholar
[19] Kohda T 2001 Regul. Pept. 1240 74
[20] Kohda T, Tsuneda A 1997 IEEE Trans. Inf. Theory 43 104
Google Scholar
[21] Richard B, Mark D, Ronald D, Michael W 2008 Constructive Approximation 28 253
Google Scholar
[22] Geršhgorin S A 1931 Izv. Akad. Nauk SSSR Ser. Fiz. Mat. 6 749
-
图 1 忽略标量
${1}/{\sqrt{m}}$ 的Bi-TpCM及其对应的Gram矩阵展示图 (a) Bi-TpCM; (b) Gram矩阵的三维渲染图; (c) Gram矩阵的等高图Figure 1. Bi-TpCM without the factor
${1}/{\sqrt{m}}$ and its Gram matrix: (a) Bi-TpCM; (b) three dimensional rendering of its Gram matrix; (c) contour map of its Gram matrix.
图 2 Bi-TpCM压缩测量一维信号的重构 (a) s = 20, 条形图; (b) s = 20, 细节图; (c) s = 30, 条形图; (d) s = 30, 细节图
Figure 2. Reconstructions of one-dimensional signal using Bi-TpCM: (a) s = 20, stem rendering; (b) s = 20, detailed drawing; (c) s = 30, stem rendering; (d) s = 30, detailed drawing.
图 3 分别使用不同的感知矩阵对稀疏度变化的x进行压缩测量时的重建性能比较 (a) 重建误差; (b) 信噪比 (dB); (c) 完美重建的概率
Figure 3. Performance comparisons for recovering x with different sparsity using various sensing matrices, respectively: (a) Recovery error; (b) SNR (dB); (c) perfect recovery probability.
图 4 原始图像和Bi-TpCM在不同采样率下的恢复图像, 其中第一行是(a) 原始“Lena”, (b)
$\varpi=0.3$ , (c)$\varpi=0.6$ , (d)$\varpi=0.8$ ; 第二行是(e) 原始“Lin”, (f)$\varpi=0.3$ , (g)$\varpi=0.6$ ,$\varpi=0.8$ Figure 4. Original and reconstructed images using Bi-TpCM at different sampling rates. The first row: (a) Original “Lena”; (b)
$\varpi=0.3$ ; (c)$\varpi=0.6$ ; (d)$\varpi=0.8$ . The second row: (e) Original “Lin”; (f)$\varpi=0.3$ ; (g)$\varpi=0.6$ ; (h)$\varpi=0.8$ .
图 5 在不同采样率下利用不同的感知矩阵对图像进行压缩测量时的重建PSNR比较 (a) “Lena”; (b) “Lin”
Figure 5. Reconstructed PSNR comparisons for image compressed sensing using different sensing matrices at various sampling rates, respectively: (a) “Lena”; (b) “Lin”.
表 1 不同感知矩阵的性能比较
Table 1. Performance comparisons of different sensing matrices.
感知矩阵 特征性质 RIP 普适性 元素性 内存消耗 支持快速计算 对应测量系统 Den-RgM 满足 Yes 随机 ${\cal{O}}(B \times mn)$/次 No — Den-Bol 满足 Yes 随机 ${\cal{O}}(mn)$/次 No — Den-CbM 满足 Yes 确定 ${\cal{O}}(B \times mn)$ No — Top-Rad 满足 Yes 随机 ${\cal{O}}(m+n-1)$/次 支持 单输入单输出LTI Cir-CaM 满足 Yes 确定 ${\cal{O}}(B \times n)$ 支持 单输入单输出LTI Bi-TpCM 满足 Yes 确定 ${\cal{O}}(b(m+d-1))$ 支持 多输入单输出LTI 注1: 表中设定存储一位十进制数需消耗B位内存, 存储元素$\pm1$需一位内存. 
DownLoad: CSV
-
[1] Candès E J, Romberg J, Tao T 2006 IEEE Trans. Inf. Theory 52 1289
Google Scholar
[2] 庄佳衍, 陈钱, 何伟基, 冒添逸 2016 物理学报 65 040501
Google Scholar
Zhuang J Y, Chen Q, He W J, Mao T Y 2016 Acta Phys. Sin. 65 040501
Google Scholar
[3] Eldar Y C, Kutyniok G 2012 Compressed Sensing: Theory and Applications (Cambridge: Cambridge University Press) pp1−5
[4] 石航, 王丽丹 2019 物理学报 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[5] Hyder M M, Mahata K 2010 IEEE Trans. Signal Process. 58 2194
Google Scholar
[6] Wang J, Shim B 2012 IEEE Trans. Signal Process. 60 4973
Google Scholar
[7] Chen S S, Donoho D L, Saunders M A 2001 SIAM Review 43 129
Google Scholar
[8] Candès E J 2008 C. R. Math. 346 589
Google Scholar
[9] Donoho D L, Huo X M 2001 IEEE Trans. Inf. Theory 47 2845
Google Scholar
[10] Lu W Z, Li W Y, Zhang W, Xia S T 2018 IEEE Trans. Signal Inf. Process. Networks 5 418
Google Scholar
[11] Ansari N, Gupta A 2017 IEEE Trans. Image Process. 26 3680
Google Scholar
[12] Haupt J, Bajwa W U, Raz G, Nowak R 2010 IEEE Trans. Inf. Theory 56 5862
Google Scholar
[13] Yu L, Barbot J P, Zheng G, Sun H 2010 IEEE Signal Process. Lett. 17 731
Google Scholar
[14] Gan H P, Li Z, Li J, Wang X, Cheng Z F 2014 Nonlinear Dyn. 78 2429
Google Scholar
[15] 郭静波, 汪韧 2014 物理学报 63 198402
Google Scholar
Guo J B, Wang R 2014 Acta Phys. Sin. 63 198402
Google Scholar
[16] 郭静波, 李佳文 2015 物理学报 64 198401
Google Scholar
Guo J B, Li J W 2015 Acta Phys. Sin. 64 198401
Google Scholar
[17] 陶太洋 2016 硕士学位论文 (无锡: 江南大学)
Tao T Y 2016 M. S. Thesis (Wuxi: Jiangnan University) (in Chinese)
[18] Kohda T 2002 Proc. IEEE 90 641
Google Scholar
[19] Kohda T 2001 Regul. Pept. 1240 74
[20] Kohda T, Tsuneda A 1997 IEEE Trans. Inf. Theory 43 104
Google Scholar
[21] Richard B, Mark D, Ronald D, Michael W 2008 Constructive Approximation 28 253
Google Scholar
[22] Geršhgorin S A 1931 Izv. Akad. Nauk SSSR Ser. Fiz. Mat. 6 749
DownLoad:
Catalog
Metrics
- Abstract views: 5421
- PDF Downloads: 83
- Cited By: 0
