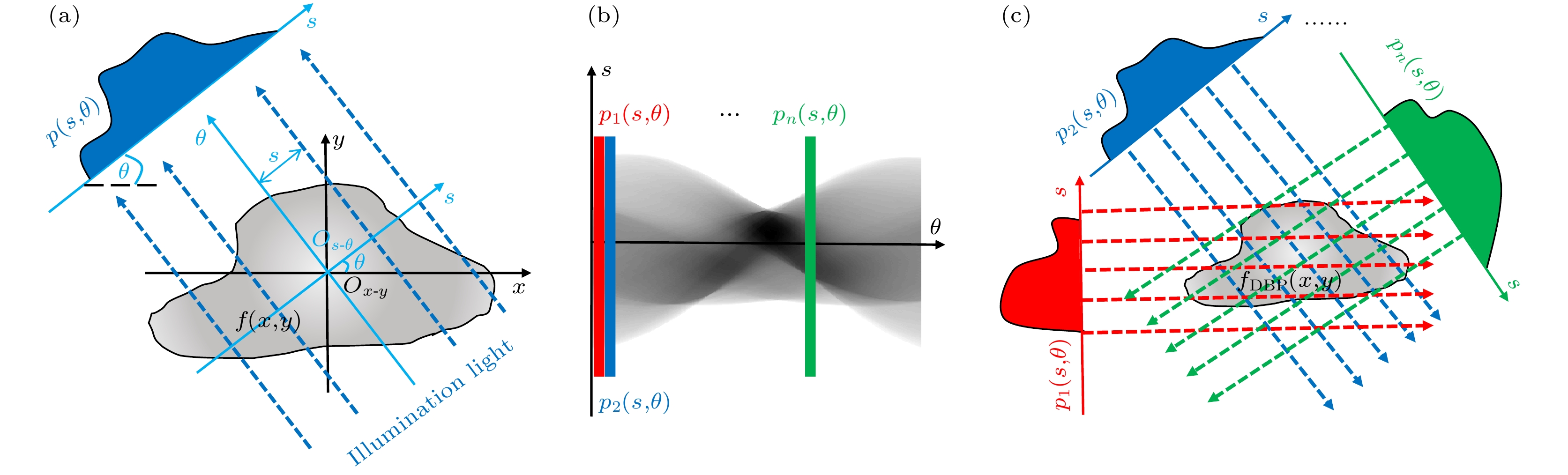
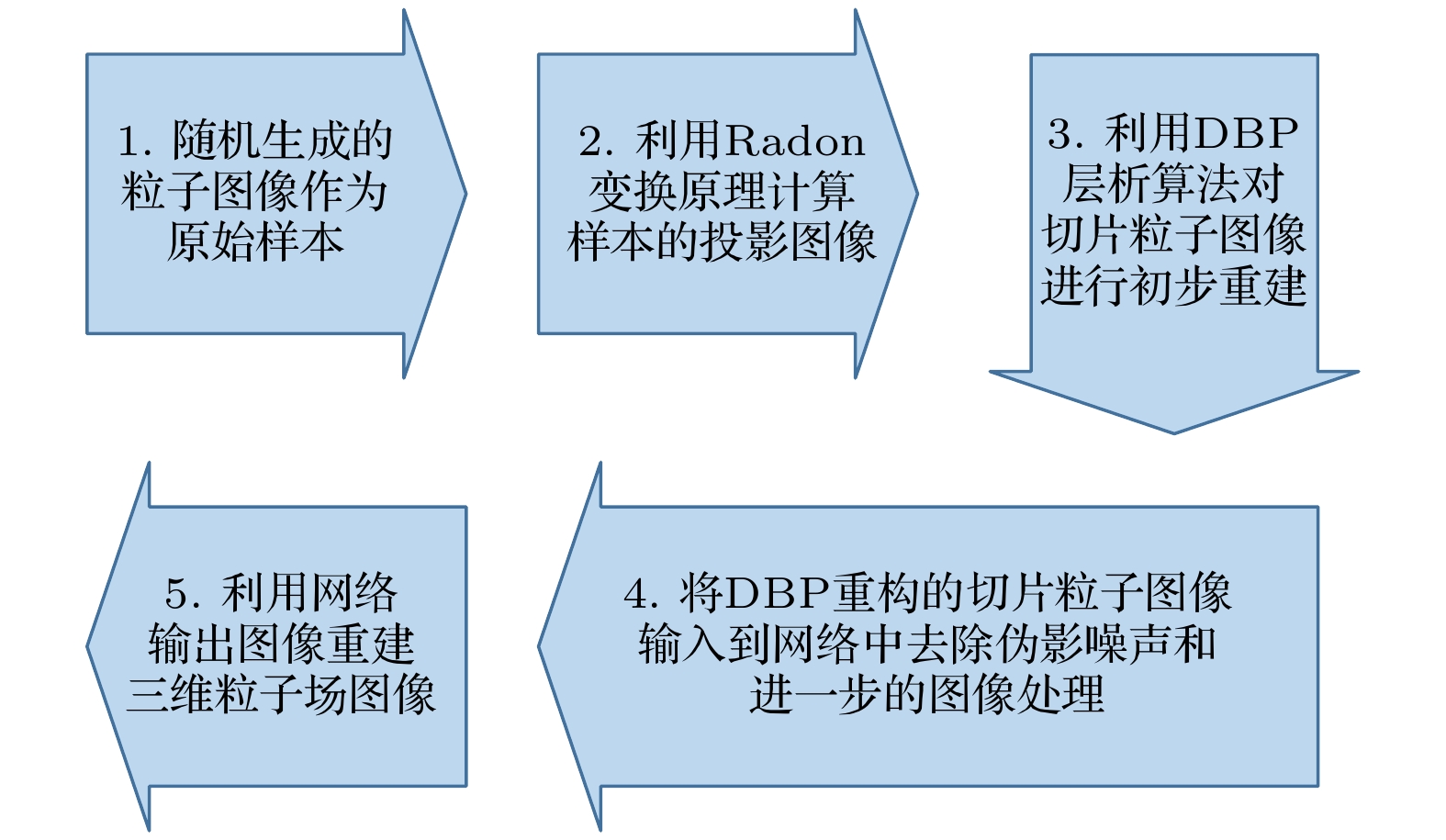
-
The realization of fast and high-quality three-dimensional particle-field image characterization is always highly desired in the areas, such as experimental fluid mechanics and biomedicine, for the micro-particle distribution status in a flow-field can characterize the field properties well. In the particle-field image reconstruction and characterization, a wildly used approach at present is the computed tomography. The great advantage of the computed tomography for particle-field image reconstruction lies in the fact that the full particle spatial distribution can be obtained and presented due to multi-angle sampling. Recently, with the development and application of deep learning technique in computed tomography, the image quality has been greatly improved by the powerful learning ability of a deep learning network. In addition, the deep learning application also makes it possible to speed up the computed tomographic imaging process from sparse-sampling due to the ability of the network to strongly extract image feature. However, sparse-sampling will lead to insufficient acquirement of the object information during sampling for the computed tomography. Therefore, a sort of artifact noise will emerge and be accompanied with the reconstructed images, and thus severely affecting the image quality. As there is no universal network approach that can be applied to all types of objects in the suppression of artifact noise, it is still a challenge in removing the sparse-sampling-induced artifact noise in the computed tomography now. Therefore, we propose and develop a specific lightweight residual and enhanced convergence neural network (LREC-net) approach for suppressing the artifact noise in the particle-field computed tomography. In this method, the network input dataset is also optimized in signal-to-noise ratio (SNR) in order to reduce the input noise and ensure the effective particle image feature extraction of the network in the imaging process. In the design of LREC-net architecture, a five-layer lightweight and dual-residual down-sampling is constructed on the basis of typical U-net and Resnet50, making the LREC-net more suitable for the particle-field image reconstruction. Moreover, a fast feature convergence module for rapid particle-field feature acquirement is added to up-sampling process of the network to further promote the network processing efficiency. Apart from the design of LREC-net network itself, the optimization of network input dataset in SNR of images is achieved by finding a fit image reconstruction algorithm that can produce higher-SNR particle images in the computed tomography. This achievement reduces the input noise as much as possible and ensures effective particle-field feature extraction by the network. The simulation analysis and experimental test demonstrate the effectiveness of the proposed LREC-net method, which involves the evaluations of SNR changes of the input-output images through the network, the proportion of residual artifact noise as ghost-particles (GPP) in the reconstructed images, and the valid-particle loss proportion (PLP). In contrast to the performances of U-net and Resnet50 under the same imaging conditions, all the data in SNR, GPP and PLP show the great improvement of the image quality due to the application of LREC-net method. Meanwhile, the designed LREC-net method also enhances the network running efficiency to a large extent due to the remarkable reduction of training time. Therefore, this work provides a new and effective approach for developing sparse-sampling-based fast and high-quality particle-field computed tomography. -
Keywords:
- particle field imaging /
- computed tomography /
- deep learning /
- noise suppression
[1] Yang L, Qiu Z, Alan H, Lu W 2012 IEEE T. Bio-Med. Eng. 59 7
Google Scholar
[2] Nayak A R, Malkiel E, McFarland M N, Twardowski M S, Sullivan J M 2021 Front. Mar. Sci. 7 572147
Google Scholar
[3] Healy S, Bakuzis A F, Goodwill P W, Attaluri A, Bulte J M, Ivkov R 2022 Wires. Nanomed. Nanobi. 14 e1779
Google Scholar
[4] Gao Q, Wang H P, Shen G X 2013 Chin. Sci. Bull. 58 4541
Google Scholar
[5] Oudheusden B W V 2013 Meas. Sci. Technol. 24 032001
Google Scholar
[6] Sun Z K, Yang L J, Wu H, Wu X 2020 J. Environ. Sci. 89 113
Google Scholar
[7] Arhatari B D, Riessen G V, Peele A 2012 Opt. Express 20 21
Google Scholar
[8] Vainiger A, Schechner Y Y, Treibitz T, Avin A, Timor D S 2019 Opt. Express 27 12
Google Scholar
[9] Cernuschi F, Rothleitner C, Clausen S, Neuschaefer-Rube U, Illemann J, Lorenzoni L, Guardamagna C, Larsen H E 2017 Powder Technol. 318 95
Google Scholar
[10] Wang H P, Gao Q, Wei R J, Wang J J 2016 Exp. Fluids 57 87
Google Scholar
[11] Kahnt M, Beche J, Brückner D, Fam Y, Sheppard T, Weissenberger T, Wittwer F, Grunwaldt J, Schwieger W, Schroer C G 2019 Optica 6 10
Google Scholar
[12] Zhou X, Dai N, Cheng X S, Thompson A, Leach R 2022 Powder Technol. 397 117018
Google Scholar
[13] Lell M M, Kachelrieß M 2020 Invest. Radiol. 55 1
Google Scholar
[14] Chen H, Zhang Y, Zhang W H, Liao P X, Li K, Zhou J L, Wang G 2017 Biomed. Opt. Express 8 679
Google Scholar
[15] Qian K, Wang Y, Shi Y, Zhu X X 2022 IEEE Trans. Geosci. Remote Sens. 60 4706116
Google Scholar
[16] Wei C, Schwarm K K, Pineda D I, Spearrin R 2021 Opt. Express 29 14
Google Scholar
[17] Zhang Z C, Liang X K, Dong X, Xie Y Q, Cao G H 2018 IEEE T. Med. Imaging 37 1407
Google Scholar
[18] Jin K H, McCann M T, Froustey E, Unser M 2017 IEEE T. Image Process. 26 9
Google Scholar
[19] Han Y, Ye J C 2018 IEEE T. Med. Imaging 37 1418
Google Scholar
[20] Gao Q, Pan S W, Wang H P, Wei R J, Wang J J 2021 AIA 3 1
Google Scholar
[21] Wu D F, Kim K, Fakhri G EI, Li Q Z 2017 IEEE T. Med. Imaging 36 2479
Google Scholar
[22] Liang J, Cai S, Xu C, Chu J 2020 IET Cyber-Syst Robot 2 1
Google Scholar
[23] Wu W W, Hu D L, Niu C, Yu H Y, Vardhanabhuti V, Wang G 2021 IEEE T. Med. Imaging 40 3002
Google Scholar
[24] Xia W, Yang Z, Zhou Q, Lu Z, Wang Z, Zhang Y 2022 Medical Image Computing and Computer Assisted Intervention 13436 790
Google Scholar
[25] Zhang C, Li Y, Chen G 2021 Med. Phys. 48 10
Google Scholar
[26] Cheslerean-Boghiu T, Hofmann F C, Schultheiß M, Pfeiffer F, Pfeiffer D, Lasser T 2023 IEEE T. Comput. Imag. 9 120
Google Scholar
[27] Gmitro A F, Tresp V, Gindi G R 1990 IEEE T. Med. Imaging 9 4
Google Scholar
[28] Horn B K P 1979 Proc. IEEE 67 12
Google Scholar
[29] Chen G H 2003 Med. Phys. 30 6
Google Scholar
[30] Chen G H, Tokalkanahalli R, Zhuang T, Nett B E, Hsieh J 2006 Med. Phys. 33 2
Google Scholar
[31] Feldkamp L A, Davis L C, Kress J W 1984 J. Opt. Soc. Am. A 1 6
Google Scholar
[32] Yang H K, Liang K C, Kang K J, Xing Y X 2019 Nucl. Sci. Tech. 30 59
Google Scholar
[33] Katsevich A 2002 Phys. Med. Biol. 47 15
Google Scholar
[34] Zeng G L 2010 Medical Image Reconstruction: A Conceptual Tutorial (Berlin: Springer) pp10–28
[35] Lechuga L, Weidlich G A 2016 Cureus 8 9
Google Scholar
[36] Schmidt-Hieber J 2020 Ann. Statist. 48 4
Google Scholar
[37] Ioffe S, Szegedy C 2015 32nd International Conference on Machine Learning Lile, France, July 07—09, 2015 p448
[38] Ronneberger O, Fischer P, Brox T 2015 Medical Image Computing and Computer-Assisted Intervention Springer, Cham, 2015 p234
[39] He K, Zhang X, Ren S, Sun J 2016 IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, USA, 2016 p770
[40] Ramachandran G N, Lakshminarayanan A V 1971 PNAS 68 9
Google Scholar
[41] Kingma D P, Ba J L 2015 arXiv: 1412. 6980 [cs.LG]
[42] Bougourzi F, Dornaika F, Taleb-Ahmed A 2022 Knowl-Based Syst. 242 108246
Google Scholar
-
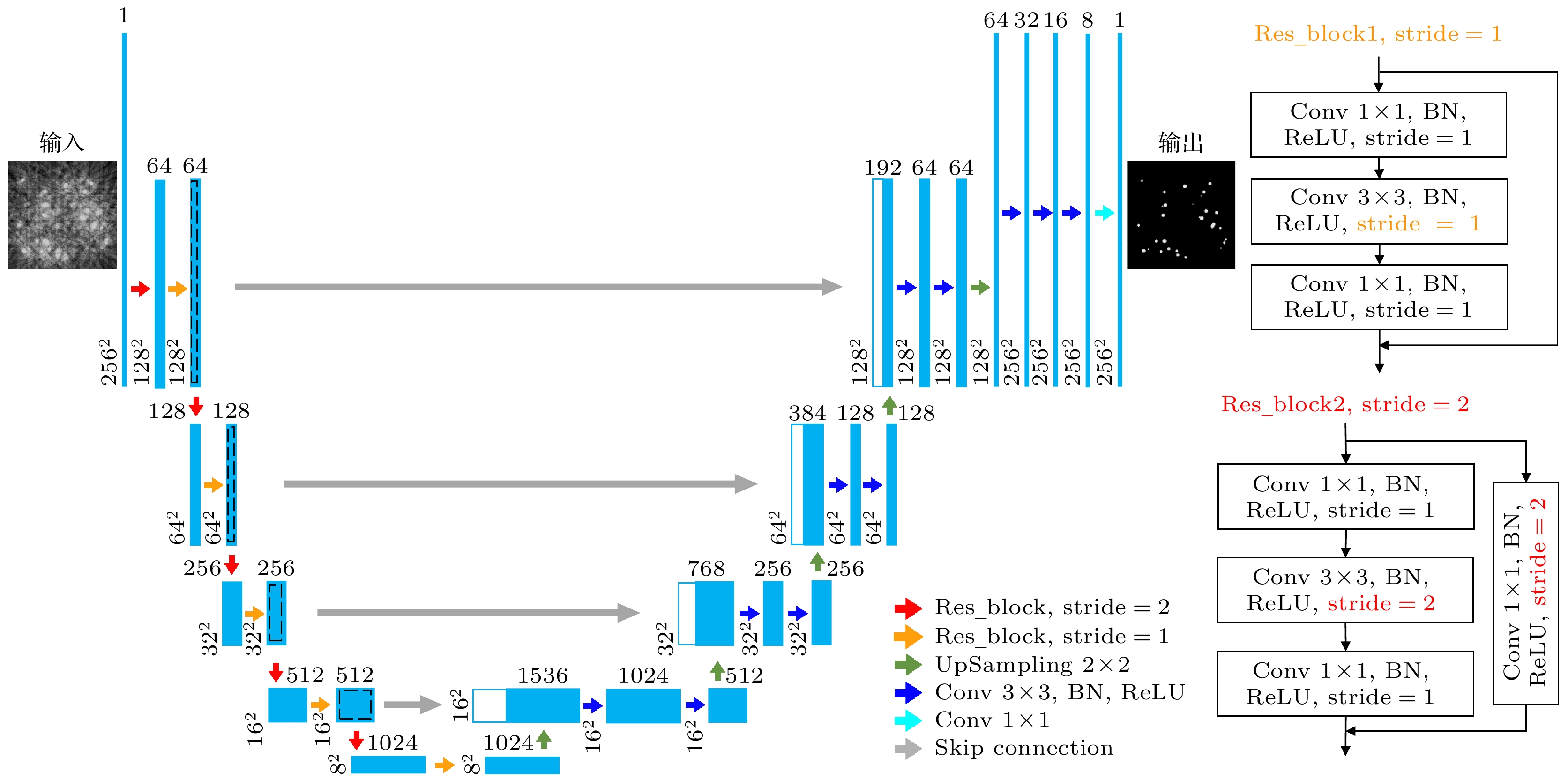
图 1 LREC-net网络架构图. Conv表示卷积; ReLU是整流线性单元, 用以提高模型的泛化能力并降低网络的计算成本[36]; BN是批量归一化处理, 可用于加速网络训练[37]
Figure 1. Diagram of LREC-net architecture. Conv denotes convolution; ReLU is the rectified linear unit, which is used to promote the generalization ability of the model and reduce the computational cost of the network[36]; BN is the batch normalization, which can be used for accelerating network training[37].
图 2 反投影CT成像方法原理图 (a)获得目标场切片在不同角度的投影图像; (b)投影图像的正弦图; (c)目标场切片的重建
Figure 2. Principle of the back-projection CT imaging approach: (a) Collection of the projections of a sliced objective-field at different angles; (b) sinogram of the projections; (c) reconstruction of the sliced objective-field.
图 3 通过比较模拟粒子层析图像的信噪比来确定网络输入数据集
Figure 3. Comparison of SNRs of the tomographic images of simulated particles for determining the network input dataset.
图 4 粒子场图像的重构和分析过程图
Figure 4. Diagram of analysis process of particle-field image reconstruction.
图 5 随机生成3组粒子场模拟切片图像(编号为①—⑥)作为原始样本(各组第1行), DBP层析重建得到的LREC-net输入图像(各组第2行), 以及最终LREC-net输出图像(各组第3行), 每组层析图像重建的样本投影数分别为5, 10和15, 每个原始样本随机包含0—40个粒子, 这些粒子具有1—9个像素的不同大小
Figure 5. Randomly-generated three groups of particle-field simulation slice images (numbered by ①–⑥) as the original samples (the first row in every group), the LREC-net input images (the second row in every group) obtained with the DBP tomographic reconstruction, and the ultimate LREC-net output images (the third row in every group), the sample projection numbers for tomographic image reconstruction of every group are 5, 10 and 15, respectively. Every original sample contains randomly 0–40 particles with different sizes of 1–9 pixels.
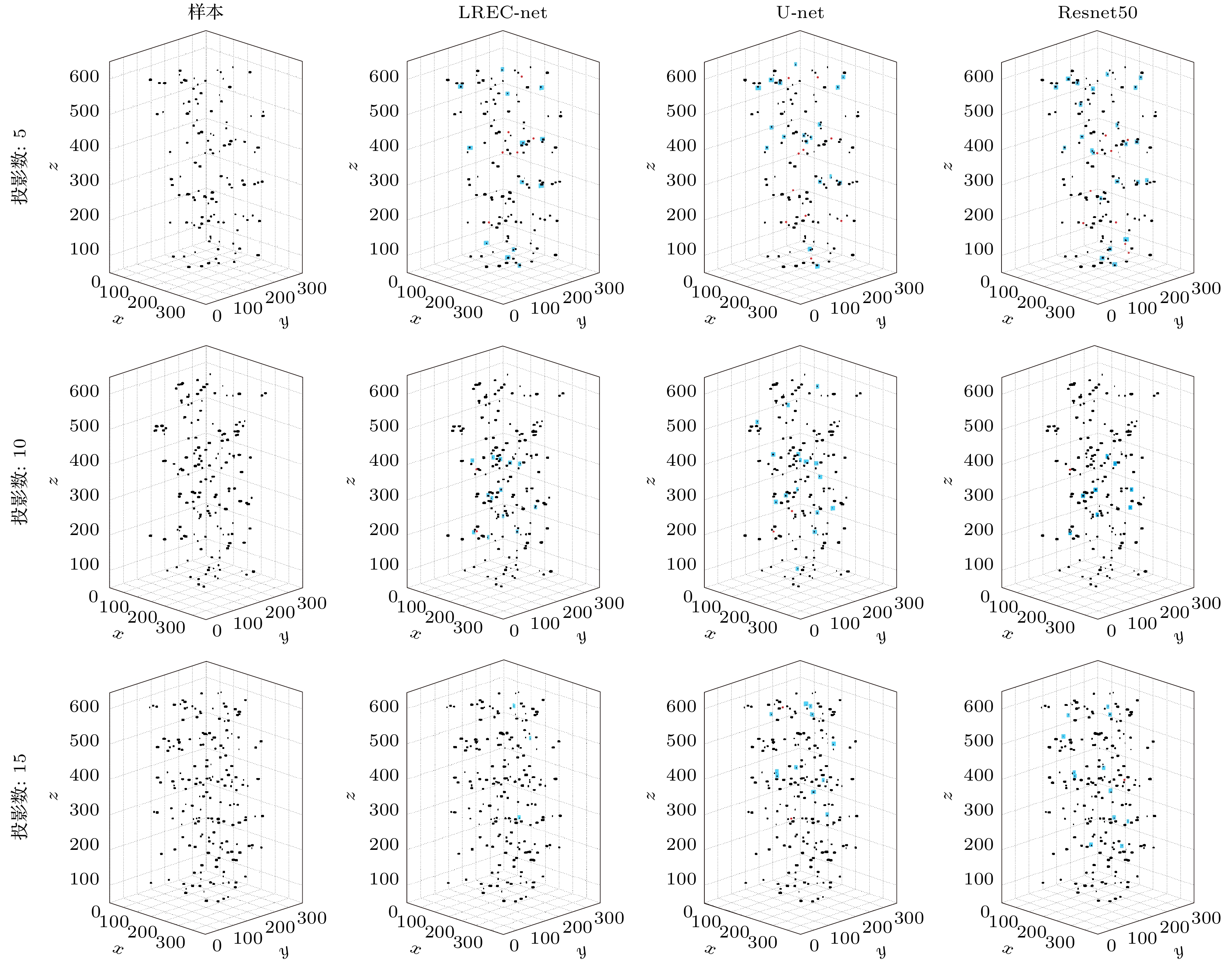
图 6 使用LREC-net, U-net和Resnet50重建三维粒子场, 其中每个三维分布包含6个切片图像, 切片图像的厚度和间隔分别为4像素和100像素, 用于层析图像重建的样本投影数分别为5, 10和15
Figure 6. Three-dimensional particle-fields reconstructed with LREC-net, U-net and Resnet50, where every three-dimensional distribution contains 6 slice images, the slice image thickness and their space are 4 pixels and 100 pixels, respectively, the sample projection numbers for tomographic image reconstruction of every group are 5, 10 and 15, respectively.
图 7 PLP (a)和GPP (b)分别随基于LREC-net, U-net和Resnet50的层析图像重建中使用的样本投影数量的变化, 用于层析图像重建的样本投影数分别为5, 10, 15, 30和60
Figure 7. PLP (a) and GPP (b) variations with the numbers of sample projections used in the tomographic reconstruction based on the LREC-net, U-net and Resnet50, respectively. Sample projection numbers for tomographic image reconstruction of every group are 5, 10, 15, 30 and 60, respectively.
图 8 LREC-net, U-net和Resnet50的训练时间, 其中构成网络输入样本集的CT图像由5—90个不同数量的样本投影图像经DBP重建计算获得
Figure 8. Training time of LREC-net, U-net and Resnet50, where the network input dataset consists of the DBP reconstruction images obtained with different numbers (5—90) of sample projections.
图 9 记录粒子投影图像的实验原理图
Figure 9. Experimental setup for recording the particle projection pictures.
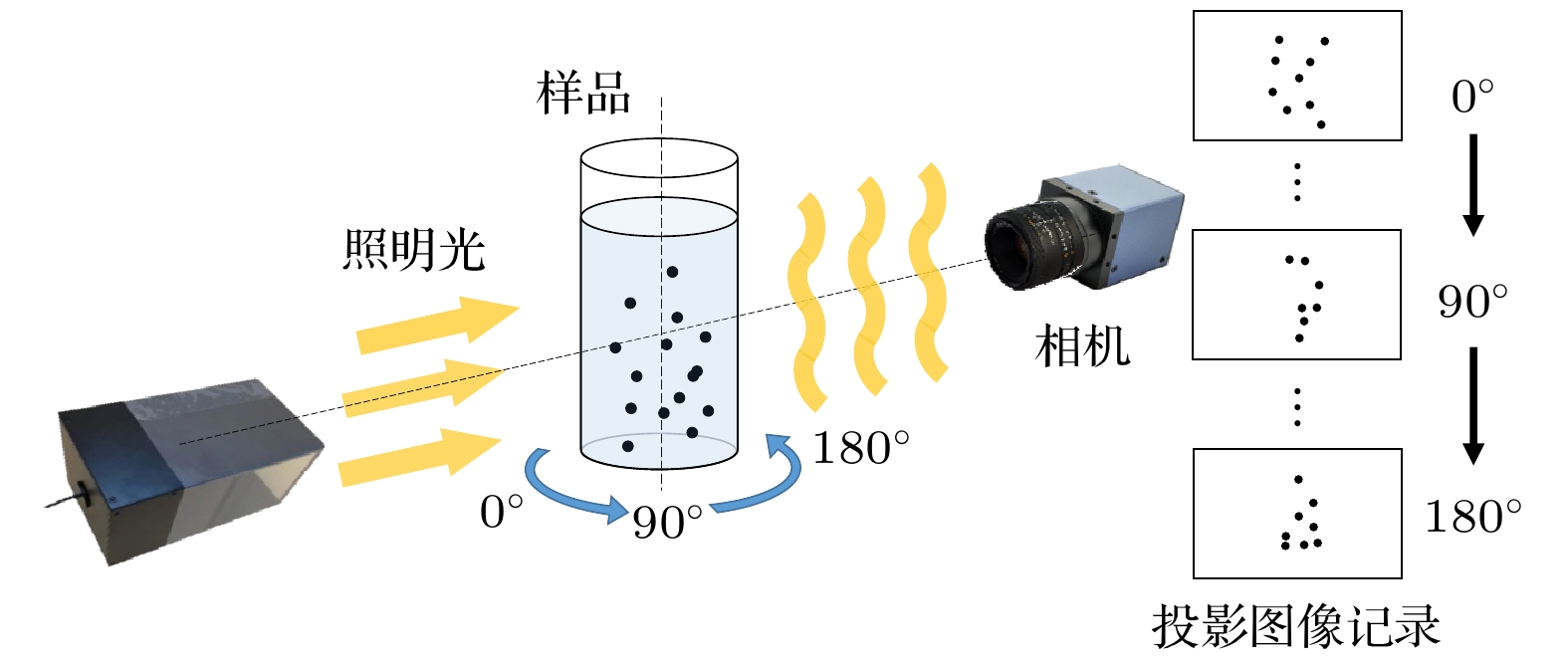
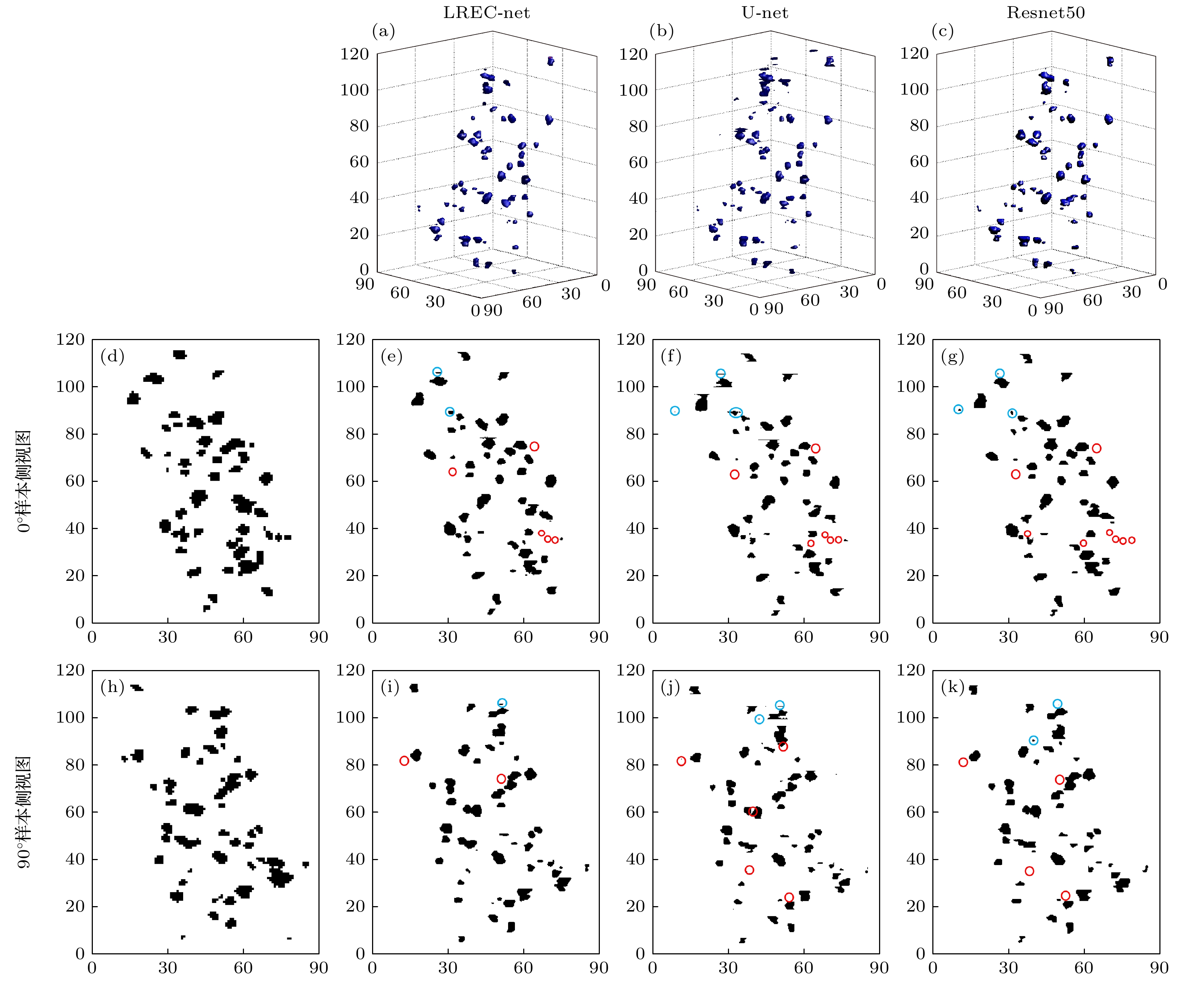
图 10 实验粒子场样品的三维重建 (a)—(c)分别使用LREC-net, U-net和Resnet50重建的三维粒子场实验样本; (d), (h)在0°和90°时记录的粒子场样品的侧视图; (e)—(g), (i)—(k)分别以图(d)和图(h)相同的角度(即0°和90°)观测图(a)—(c)的侧视图
Figure 10. Experimental three-dimensional reconstruction of particle-field sample: (a)–(c) Three-dimensional reconstructed images of the particle-field sample with LREC-net, U-net and Resnet50, respectively; (d), (h) side-views of particle-field sample recorded at 0° and 90°, respectively; (e)–(g), (i)–(k) side-views of panels (a)–(c) observed at the same angles as panels (d) and (h) (i. e. the 0° and 90°), respectively.
表 1 三种网络的下采样结构及其网络训练参数数量
Table 1. Down-sampling constitutions and the training parameter quantity of three networks.
层数 LREC-net U-net Resnet50 1 Res_block2, stride = 2 3×3 Conv 7×7 Conv, stride = 2 Res_block1, stride = 1 3×3 Conv 2×2 Maxpool 2 Res_block2, stride = 2 3×3 Conv 3×3 Maxpool Res_block1, stride = 1 3×3 Conv Res_block2, stride = 1 2×2 Maxpool Res_block1, stride = 1 Res_block1, stride = 1 3 Res_block2, stride = 2 3×3 Conv Res_block2, stride = 2 Res_block1, stride = 1 3×3 Conv Res_block1, stride = 1 2×2 Maxpool Res_block1, stride = 1 Res_block1, stride = 1 4 Res_block2, stride = 2 3×3 Conv Res_block2, stride = 2 Res_block1, stride = 1 3×3 Conv Res_block1, stride = 1 2×2 Maxpool Res_block1, stride = 1 Res_block1, stride = 1 Res_block1, stride = 1 Res_block1, stride = 1 5 Res_block2, stride = 2 3×3 Conv Res_block2, stride = 2 Res_block1, stride = 1 3×3 Conv Res_block1, stride = 1 Res_block1, stride = 1 训练参数数量 3, 529, 040 18, 842, 048 23, 581, 440 轻量化单元数 10 0 16 
DownLoad: CSV
表 2 实验粒子场重建侧视图的PLP和GPP值
Table 2. PLPs and GPPs of the reconstructed side-views of the experimental particle-field.
视图方向 评价指标 LREC-net/% U-net/% Resnet50/% 0° PLP 10 12 16 GPP 4 6 6 90° PLP 4 10 8 GPP 2 4 4
DownLoad: CSV
-
[1] Yang L, Qiu Z, Alan H, Lu W 2012 IEEE T. Bio-Med. Eng. 59 7
Google Scholar
[2] Nayak A R, Malkiel E, McFarland M N, Twardowski M S, Sullivan J M 2021 Front. Mar. Sci. 7 572147
Google Scholar
[3] Healy S, Bakuzis A F, Goodwill P W, Attaluri A, Bulte J M, Ivkov R 2022 Wires. Nanomed. Nanobi. 14 e1779
Google Scholar
[4] Gao Q, Wang H P, Shen G X 2013 Chin. Sci. Bull. 58 4541
Google Scholar
[5] Oudheusden B W V 2013 Meas. Sci. Technol. 24 032001
Google Scholar
[6] Sun Z K, Yang L J, Wu H, Wu X 2020 J. Environ. Sci. 89 113
Google Scholar
[7] Arhatari B D, Riessen G V, Peele A 2012 Opt. Express 20 21
Google Scholar
[8] Vainiger A, Schechner Y Y, Treibitz T, Avin A, Timor D S 2019 Opt. Express 27 12
Google Scholar
[9] Cernuschi F, Rothleitner C, Clausen S, Neuschaefer-Rube U, Illemann J, Lorenzoni L, Guardamagna C, Larsen H E 2017 Powder Technol. 318 95
Google Scholar
[10] Wang H P, Gao Q, Wei R J, Wang J J 2016 Exp. Fluids 57 87
Google Scholar
[11] Kahnt M, Beche J, Brückner D, Fam Y, Sheppard T, Weissenberger T, Wittwer F, Grunwaldt J, Schwieger W, Schroer C G 2019 Optica 6 10
Google Scholar
[12] Zhou X, Dai N, Cheng X S, Thompson A, Leach R 2022 Powder Technol. 397 117018
Google Scholar
[13] Lell M M, Kachelrieß M 2020 Invest. Radiol. 55 1
Google Scholar
[14] Chen H, Zhang Y, Zhang W H, Liao P X, Li K, Zhou J L, Wang G 2017 Biomed. Opt. Express 8 679
Google Scholar
[15] Qian K, Wang Y, Shi Y, Zhu X X 2022 IEEE Trans. Geosci. Remote Sens. 60 4706116
Google Scholar
[16] Wei C, Schwarm K K, Pineda D I, Spearrin R 2021 Opt. Express 29 14
Google Scholar
[17] Zhang Z C, Liang X K, Dong X, Xie Y Q, Cao G H 2018 IEEE T. Med. Imaging 37 1407
Google Scholar
[18] Jin K H, McCann M T, Froustey E, Unser M 2017 IEEE T. Image Process. 26 9
Google Scholar
[19] Han Y, Ye J C 2018 IEEE T. Med. Imaging 37 1418
Google Scholar
[20] Gao Q, Pan S W, Wang H P, Wei R J, Wang J J 2021 AIA 3 1
Google Scholar
[21] Wu D F, Kim K, Fakhri G EI, Li Q Z 2017 IEEE T. Med. Imaging 36 2479
Google Scholar
[22] Liang J, Cai S, Xu C, Chu J 2020 IET Cyber-Syst Robot 2 1
Google Scholar
[23] Wu W W, Hu D L, Niu C, Yu H Y, Vardhanabhuti V, Wang G 2021 IEEE T. Med. Imaging 40 3002
Google Scholar
[24] Xia W, Yang Z, Zhou Q, Lu Z, Wang Z, Zhang Y 2022 Medical Image Computing and Computer Assisted Intervention 13436 790
Google Scholar
[25] Zhang C, Li Y, Chen G 2021 Med. Phys. 48 10
Google Scholar
[26] Cheslerean-Boghiu T, Hofmann F C, Schultheiß M, Pfeiffer F, Pfeiffer D, Lasser T 2023 IEEE T. Comput. Imag. 9 120
Google Scholar
[27] Gmitro A F, Tresp V, Gindi G R 1990 IEEE T. Med. Imaging 9 4
Google Scholar
[28] Horn B K P 1979 Proc. IEEE 67 12
Google Scholar
[29] Chen G H 2003 Med. Phys. 30 6
Google Scholar
[30] Chen G H, Tokalkanahalli R, Zhuang T, Nett B E, Hsieh J 2006 Med. Phys. 33 2
Google Scholar
[31] Feldkamp L A, Davis L C, Kress J W 1984 J. Opt. Soc. Am. A 1 6
Google Scholar
[32] Yang H K, Liang K C, Kang K J, Xing Y X 2019 Nucl. Sci. Tech. 30 59
Google Scholar
[33] Katsevich A 2002 Phys. Med. Biol. 47 15
Google Scholar
[34] Zeng G L 2010 Medical Image Reconstruction: A Conceptual Tutorial (Berlin: Springer) pp10–28
[35] Lechuga L, Weidlich G A 2016 Cureus 8 9
Google Scholar
[36] Schmidt-Hieber J 2020 Ann. Statist. 48 4
Google Scholar
[37] Ioffe S, Szegedy C 2015 32nd International Conference on Machine Learning Lile, France, July 07—09, 2015 p448
[38] Ronneberger O, Fischer P, Brox T 2015 Medical Image Computing and Computer-Assisted Intervention Springer, Cham, 2015 p234
[39] He K, Zhang X, Ren S, Sun J 2016 IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, USA, 2016 p770
[40] Ramachandran G N, Lakshminarayanan A V 1971 PNAS 68 9
Google Scholar
[41] Kingma D P, Ba J L 2015 arXiv: 1412. 6980 [cs.LG]
[42] Bougourzi F, Dornaika F, Taleb-Ahmed A 2022 Knowl-Based Syst. 242 108246
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 536
- PDF Downloads: 28
- Cited By: 0
