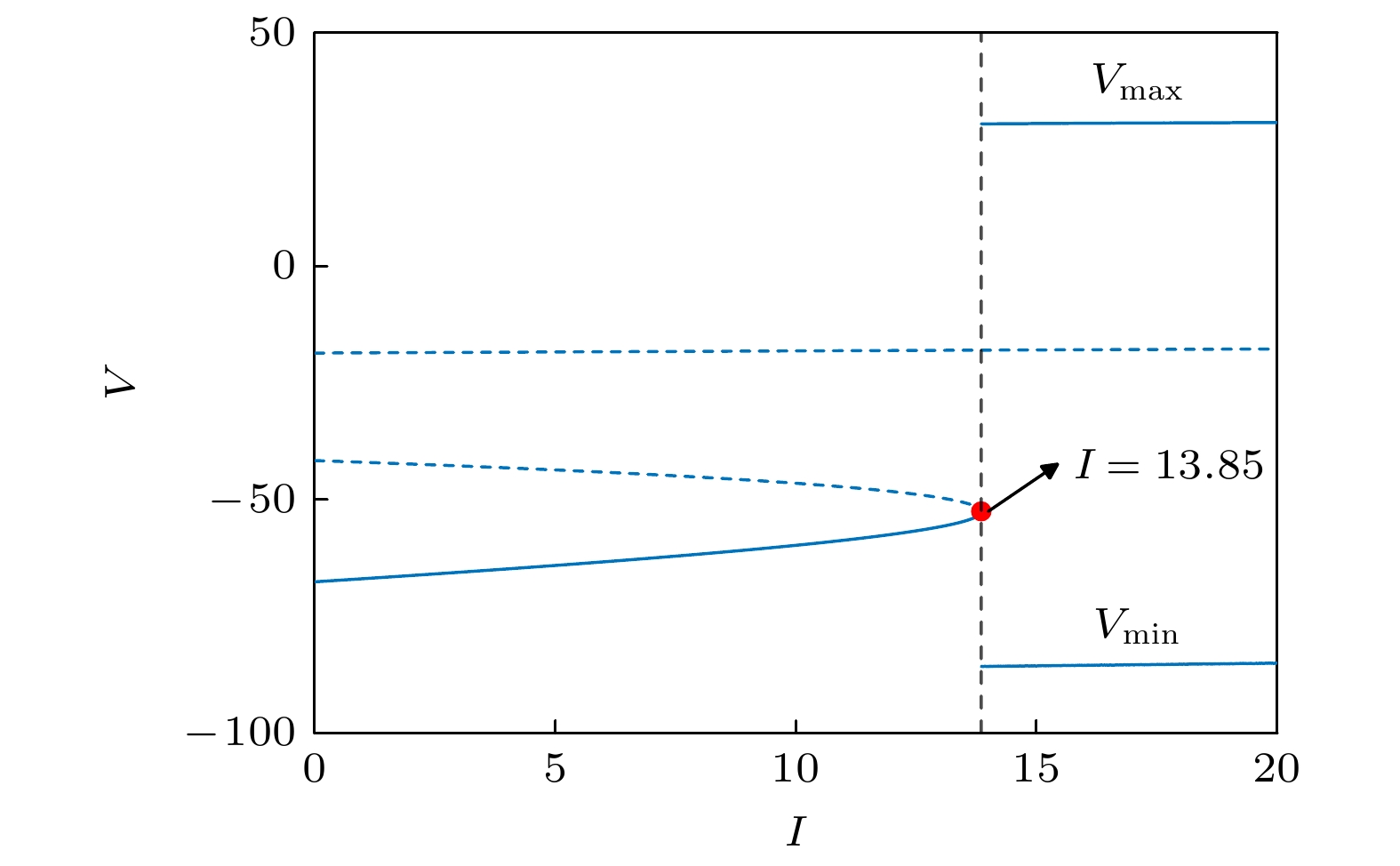
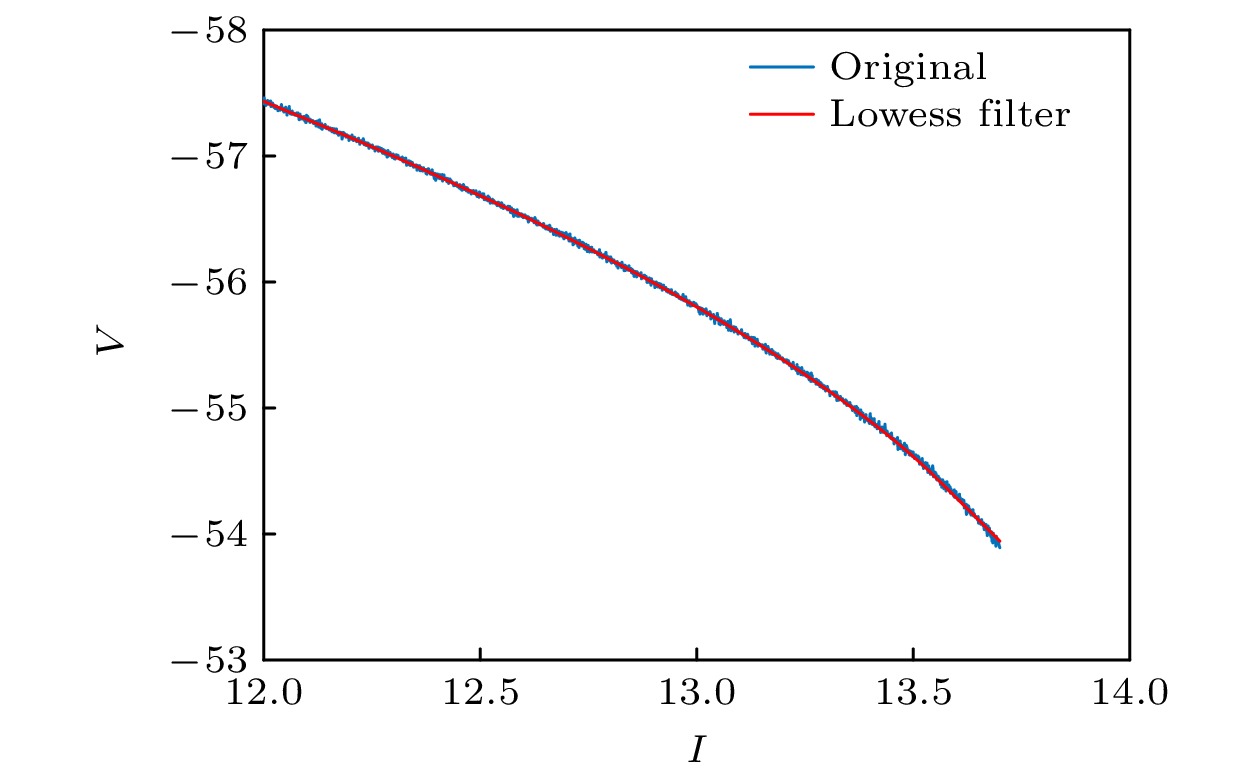
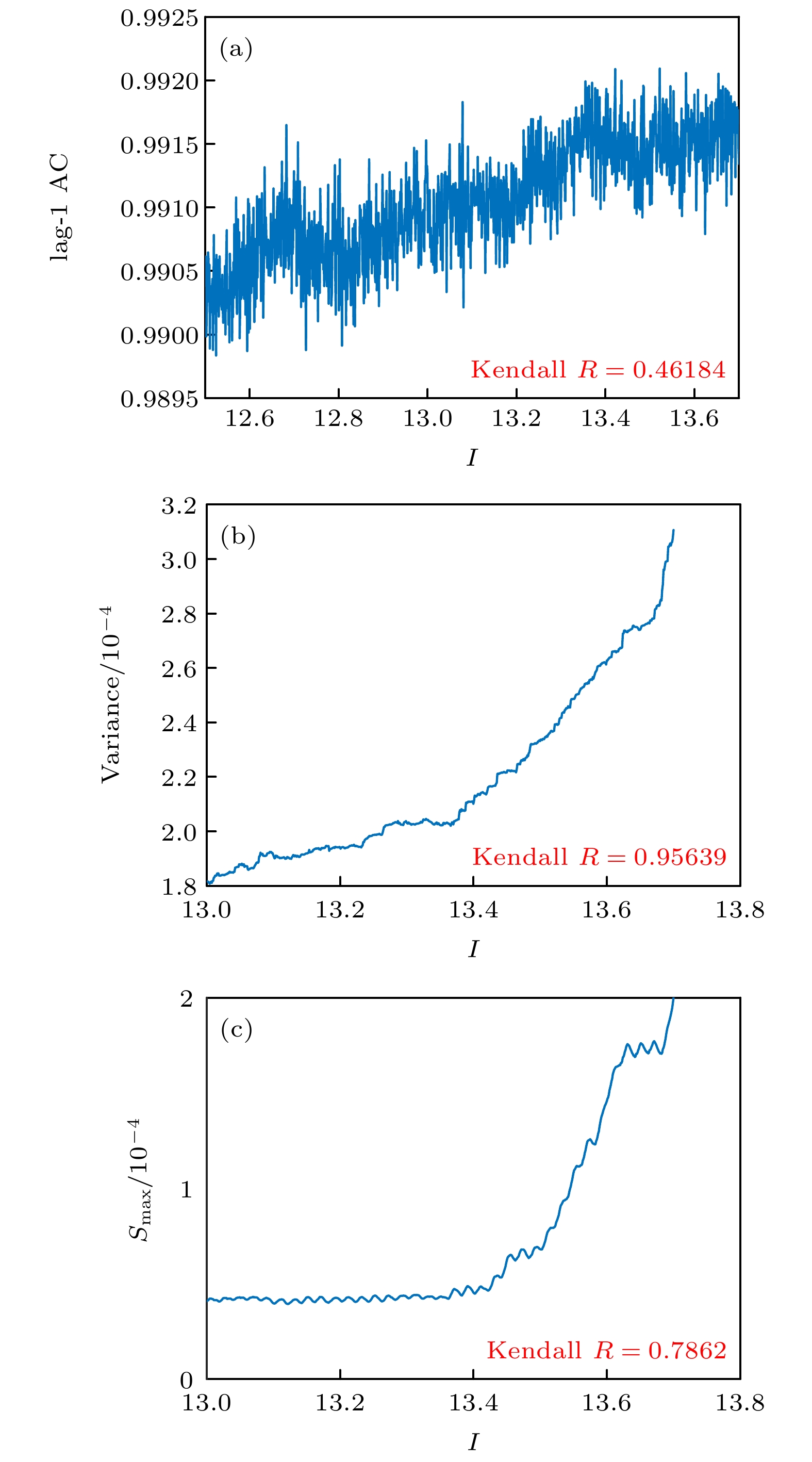
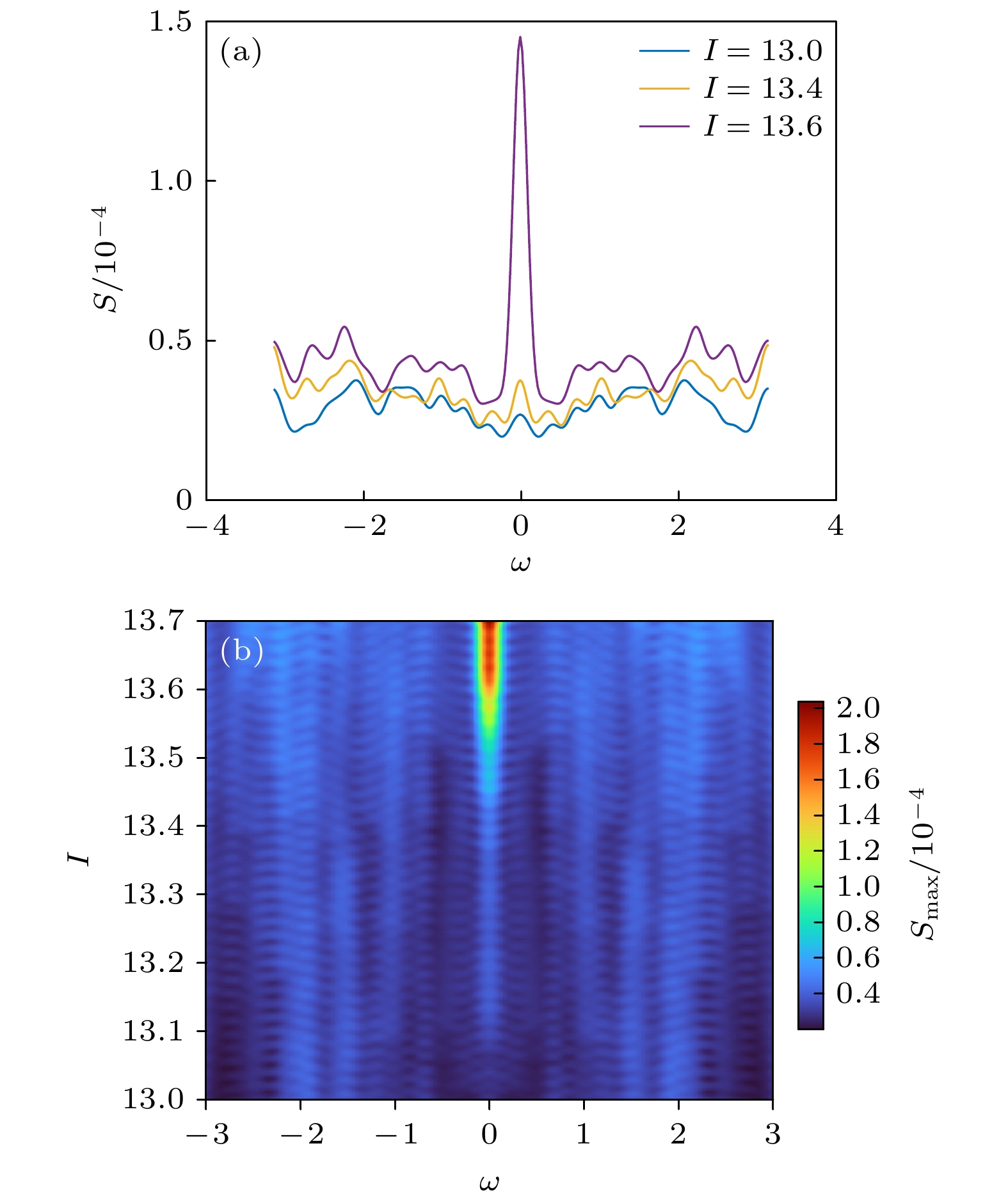
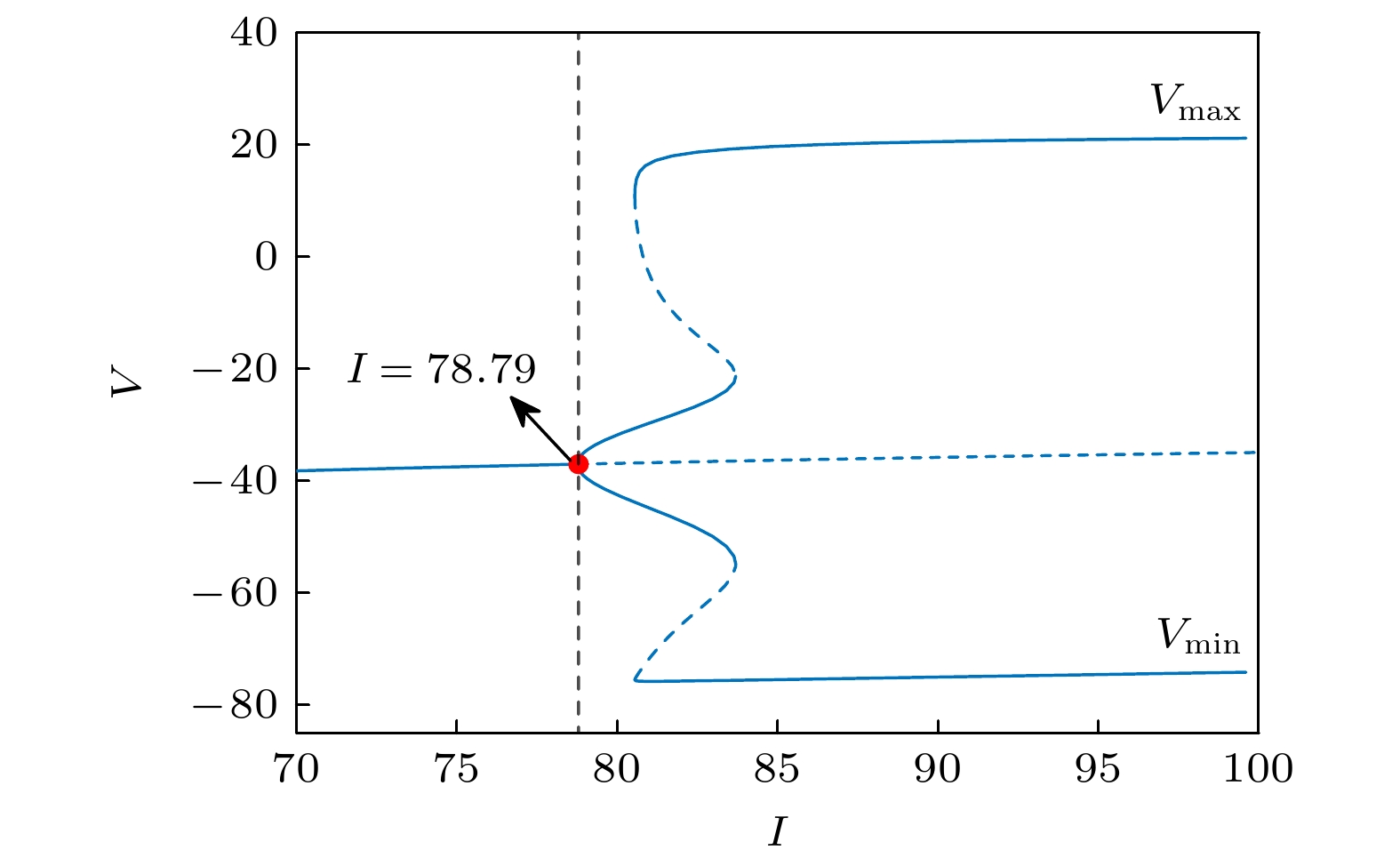
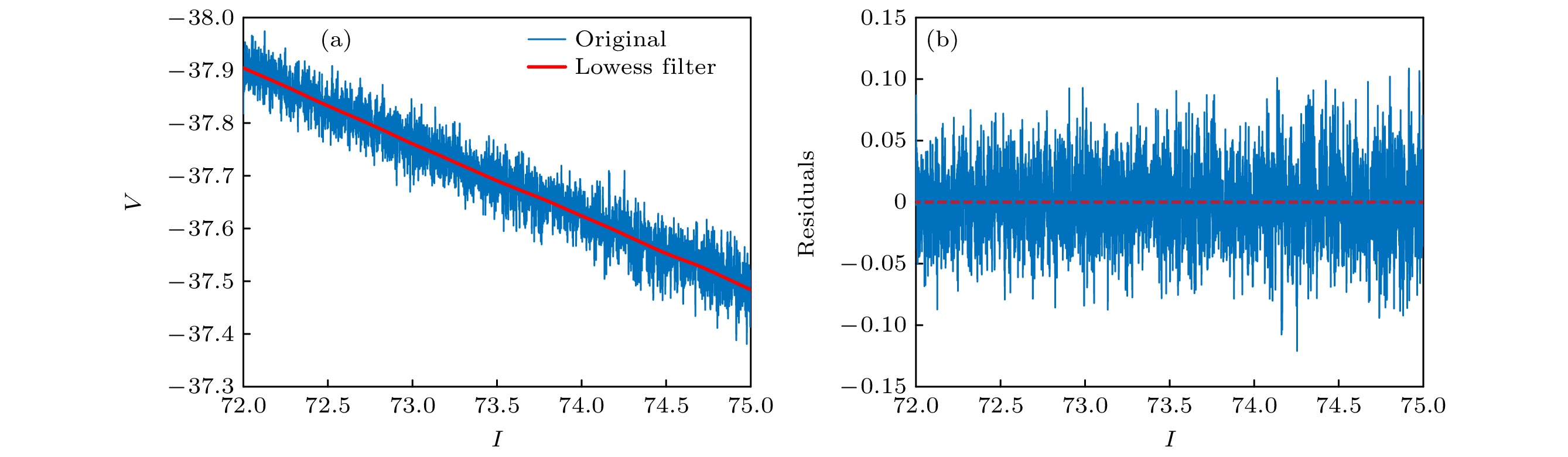
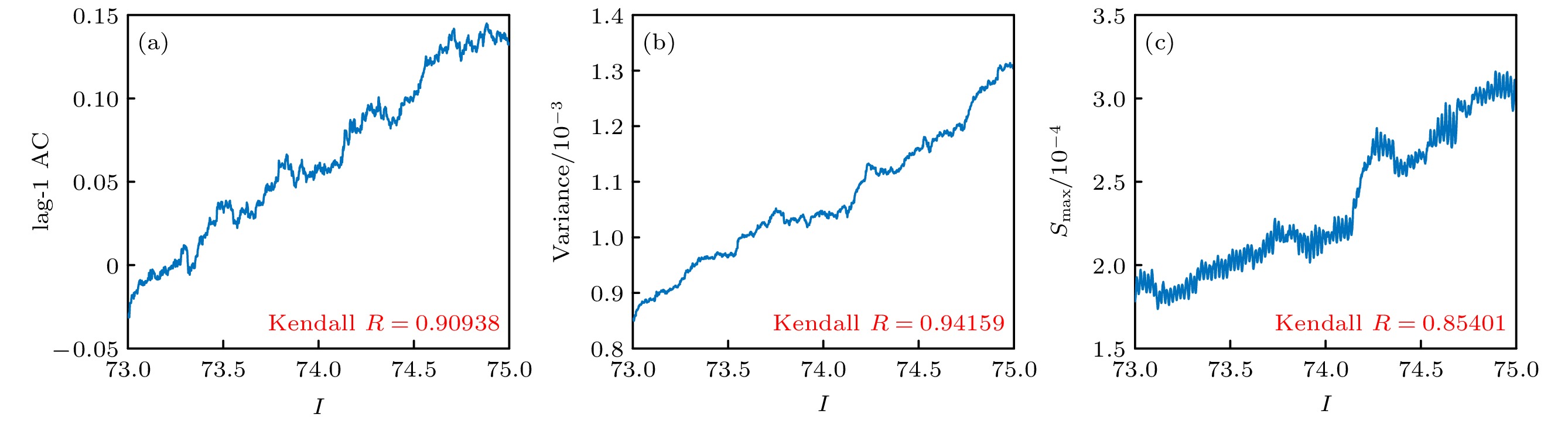
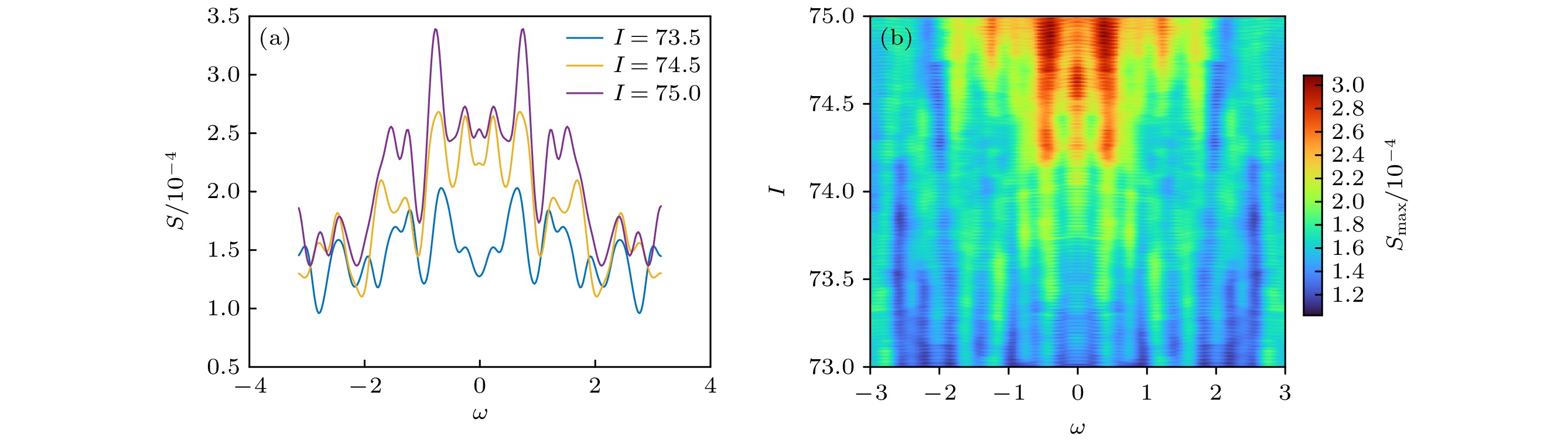
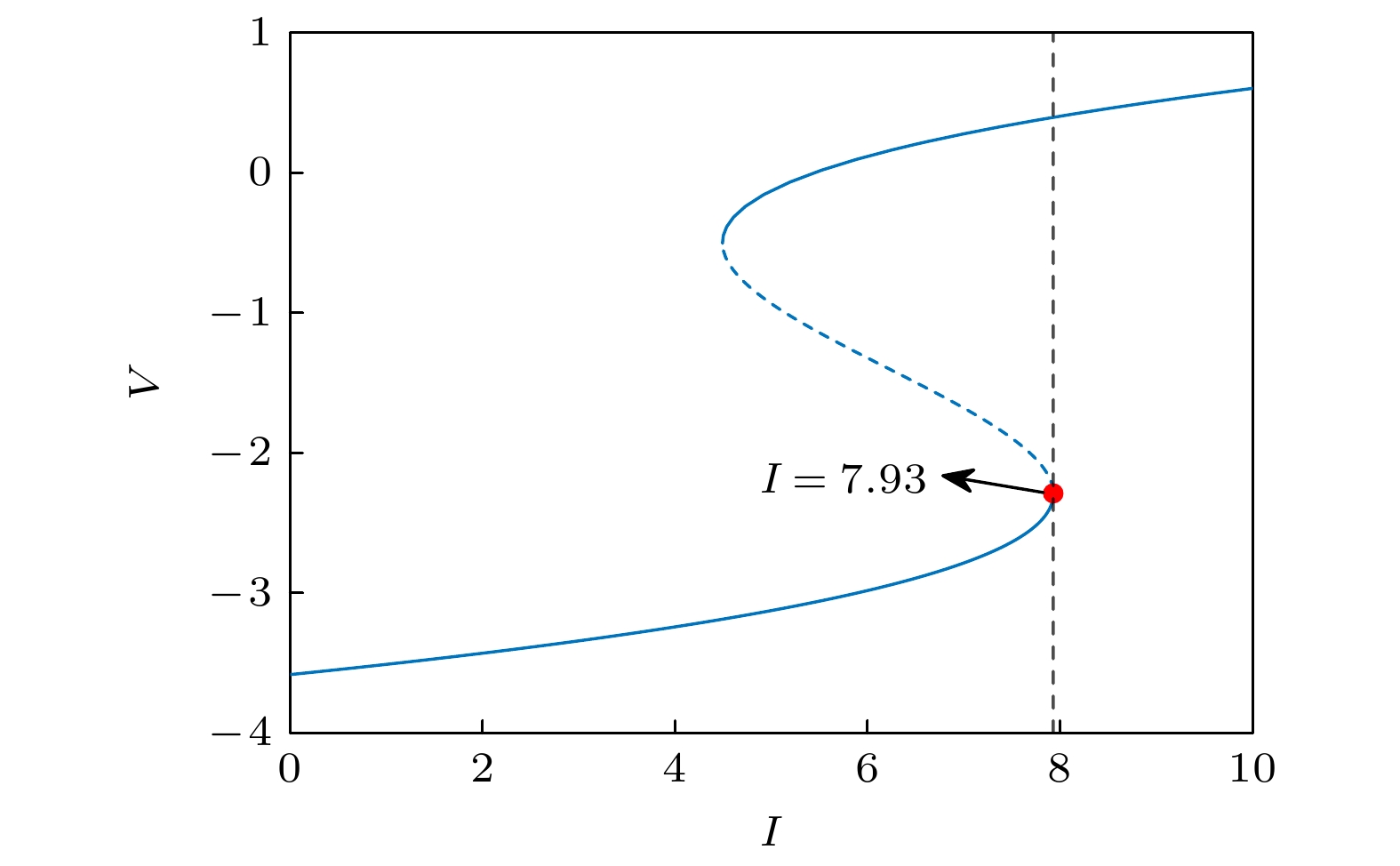
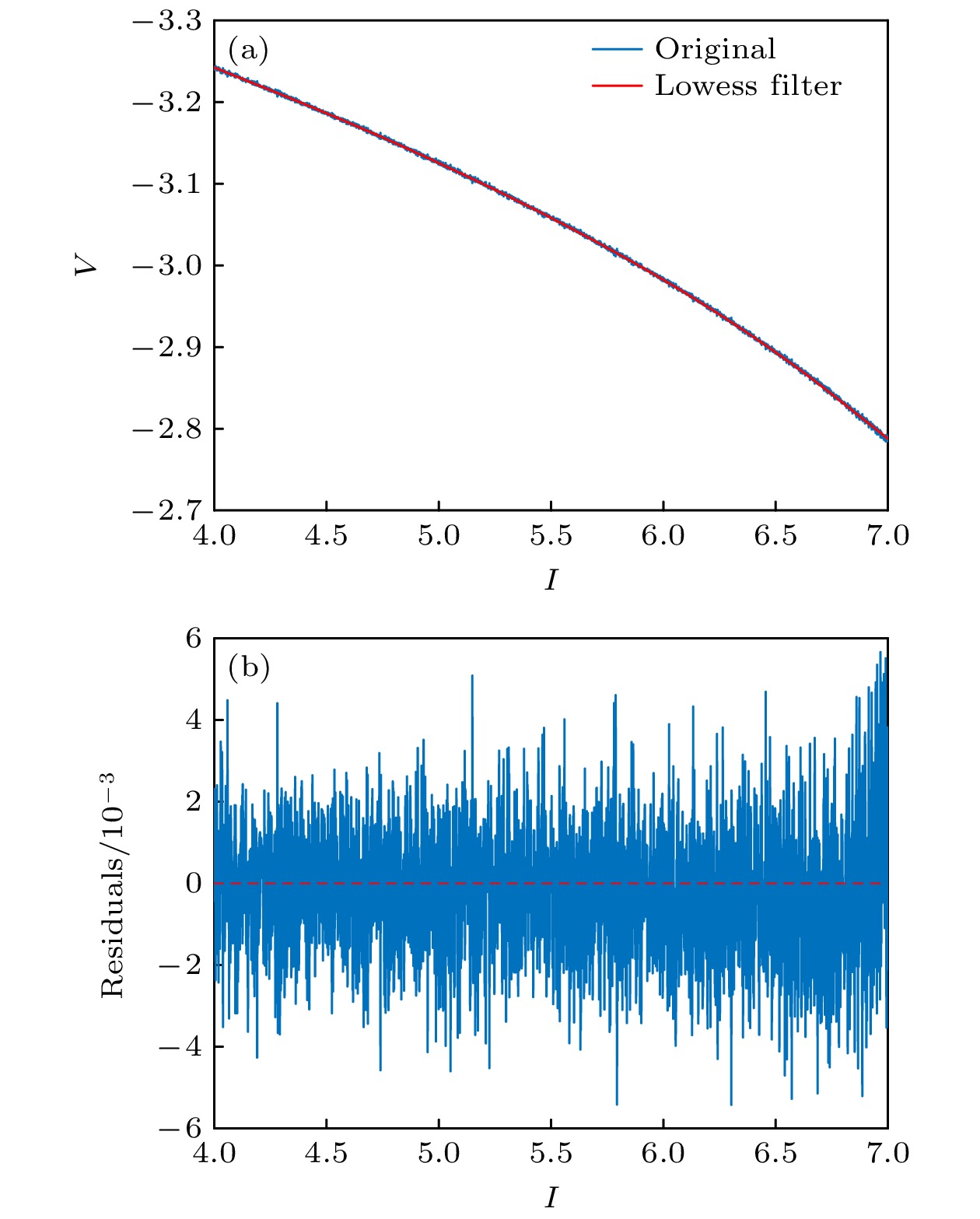
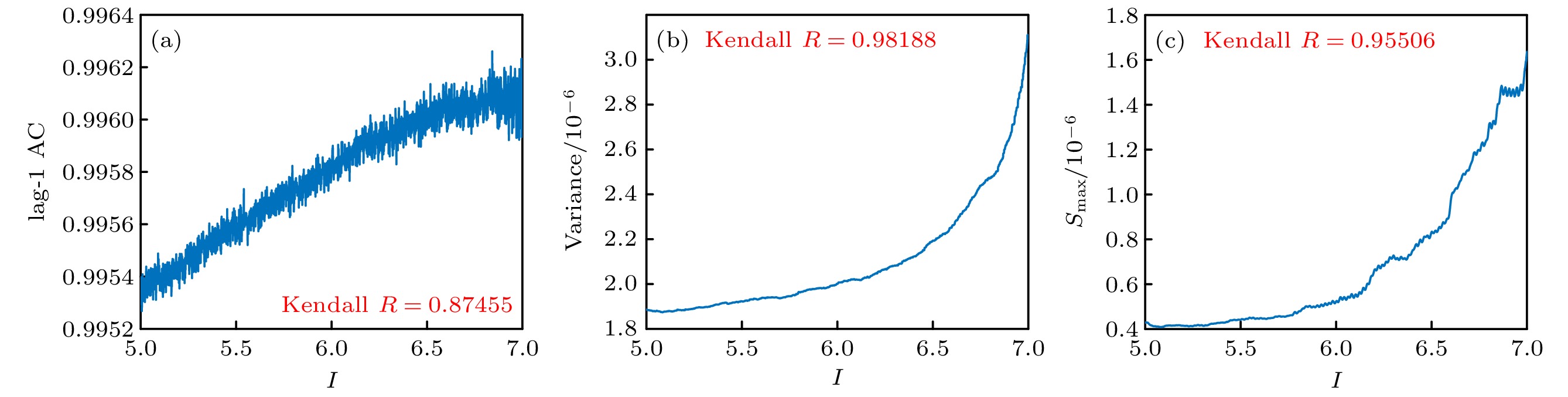
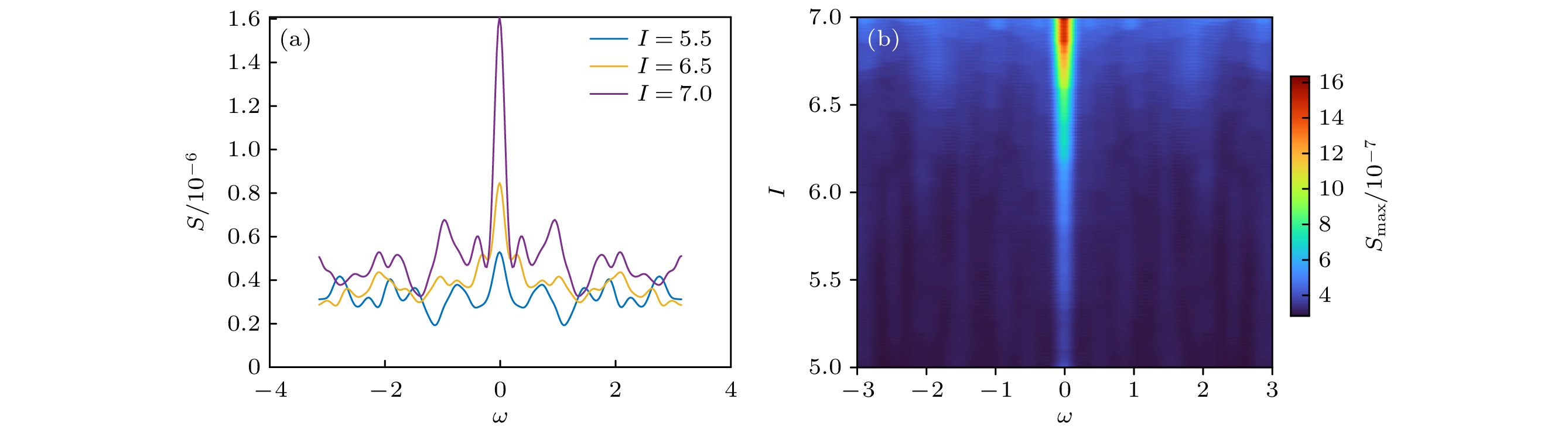
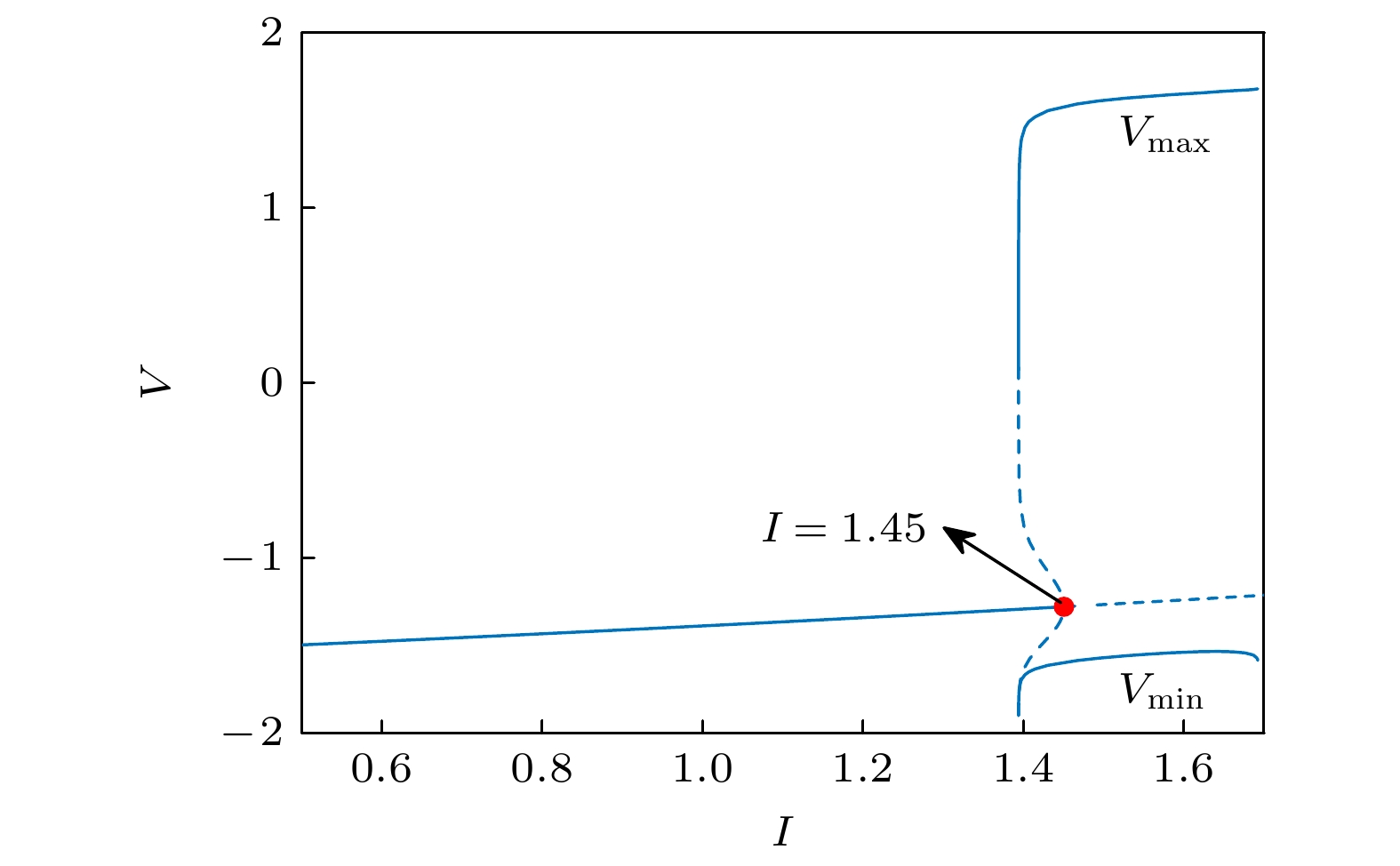
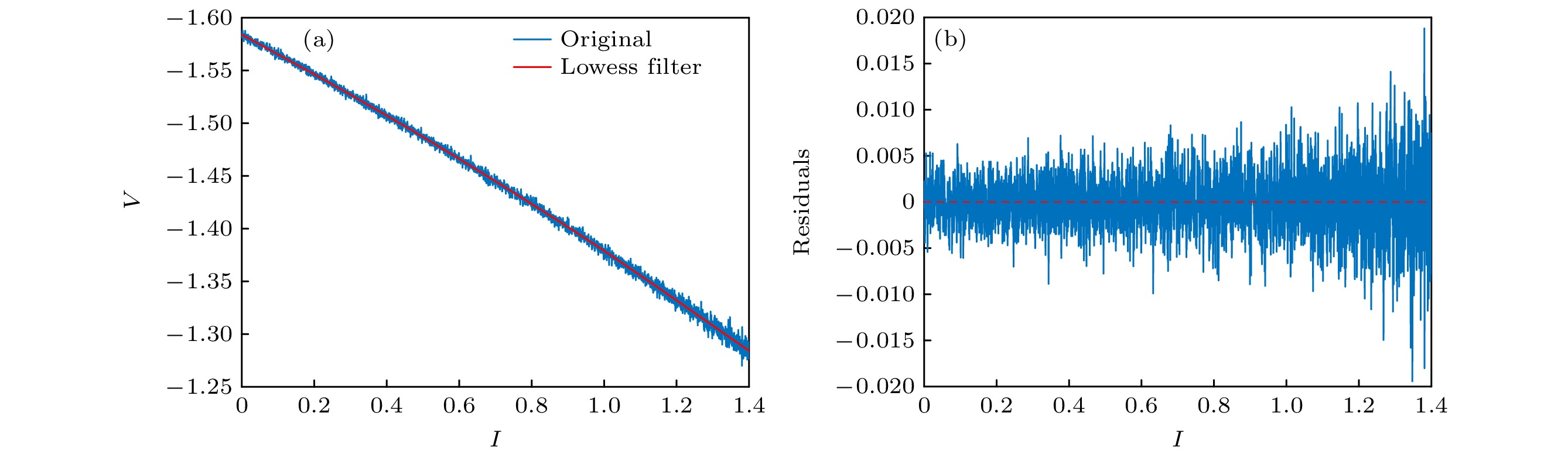
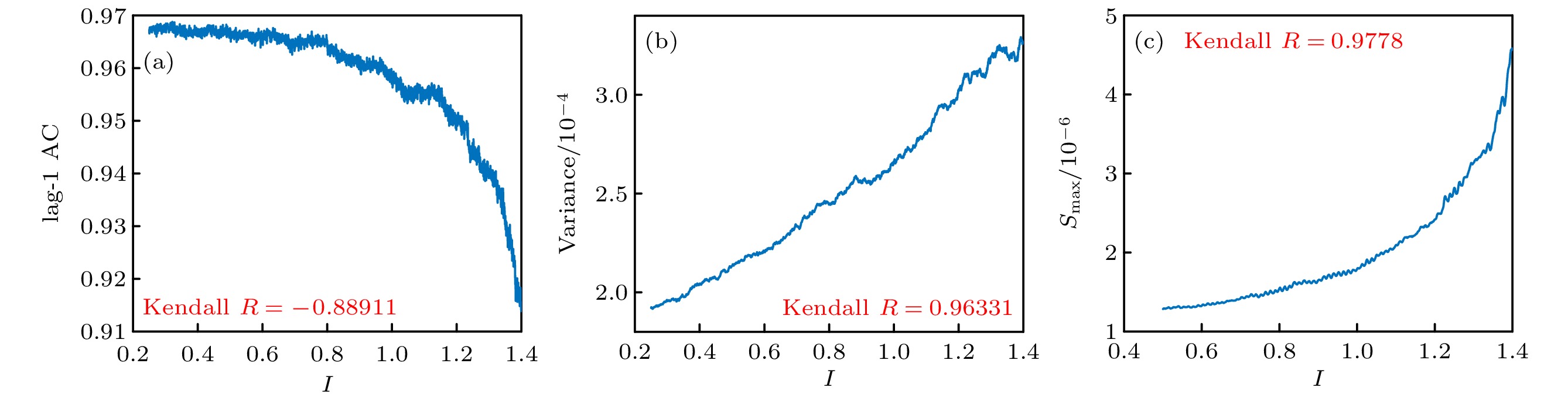
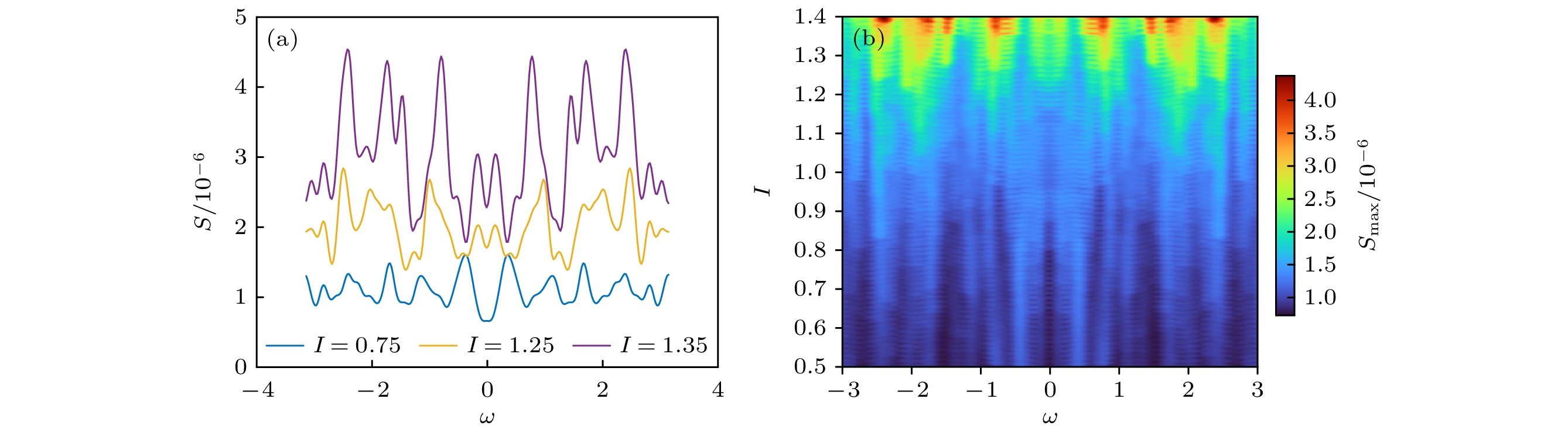
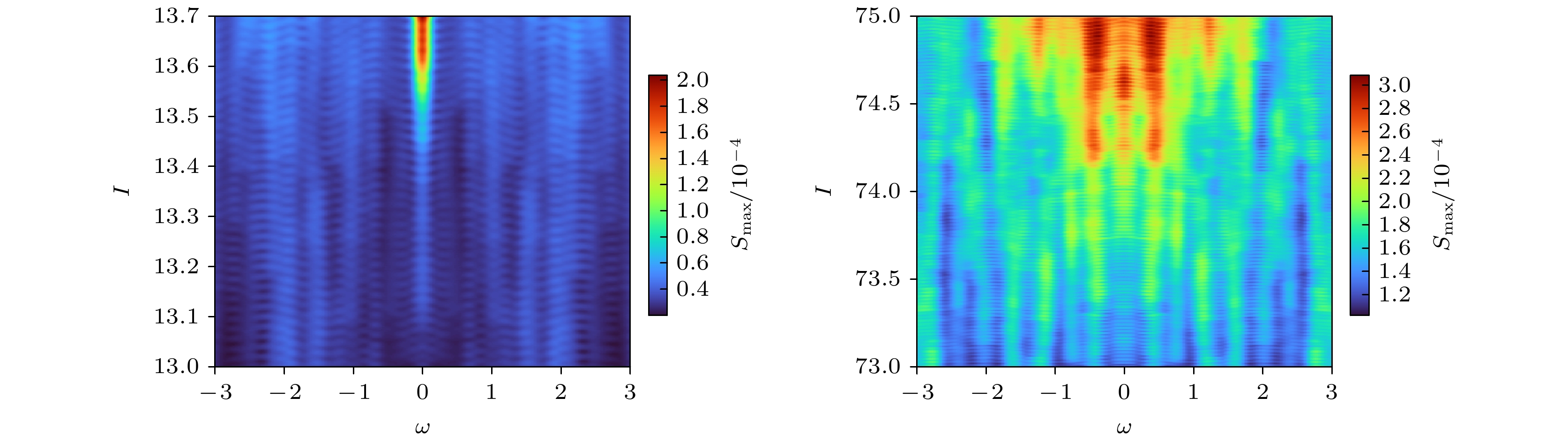
-
Brain diseases often occur simultaneously with critical changes in neural system and abnormal neuronal firing. Studying the early warning signals (EWSs) of critical changes can provide a promising approach for predicting neuronal firing behaviors, which is conducible to the early diagnosis and prevention of brain diseases. Traditional EWSs, such as autocorrelation and variance, have been widely used to detect the critical transitions in various dynamical systems. However, these methods have limitations in distinguishing different types of bifurcations. In contrast, the EWSs with power spectrum have shown a significant advantage in not only predicting bifurcation points but also distinguishing the types of bifurcations involved. Previous studies have demonstrated its predictive capability in climate and ecological models. Based on this, this study applies the EWS with power spectrum to neuronal systems in order to predict the neuronal firing behaviors and distinguish different classes of neuronal excitability. Specifically, we compute the EWSs before the occurrence of saddle-node bifurcation on the invariant circle and subcritical Hopf bifurcation in the Morris-Lecar neuron model. Additionally, we extend the analysis to the Hindmarsh-Rose model, calculating the EWSs before both saddle-node bifurcation and supercritical Hopf bifurcation. This study contains the four types of codimension-1 bifurcations corresponding to the neuronal firing. For comparison, we also calculate two types of conventional EWSs: lag-1 autocorrelation and variance. In numerical simulations, the stochastic differential equations are simulated by the Euler-Maruyama method. Then, the simulated responses are detrended by the Lowess filter. Finally, the EWSs are calculated by using the rolling window method to ensure the detection of EWS before bifurcation points. Our results show that the EWS with power spectrum can effectively predict the bifurcation points, which means that it can predict neuronal firing activities. Compared with the lag-1 autocorrelation and the variance, the EWSs with power spectrum not only accurately predict the neuronal firing, but also distinguish the classes of excitability in neurons. That is, according to the different characteristics of the power spectrum frequencies, the EWS with power spectrum can effectively distinguish between saddle-node bifurcations and Hopf bifurcations during neuronal firing. This work provides a novel approach for predicting the critical transitions in neural system, with potential applications in diagnosing and treating brain diseases.
-
Keywords:
- neurodynamics /
- power spectrum /
- critical transitions /
- early warning signals
[1] Grziwotz F, Chang C W, Dakos V, et al. 2023 Sci. Adv. 9 eabq4558
Google Scholar
[2] Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Boca Raton: CRC Press) pp70–80
[3] Maturana M I, Meisel C, Dell K, et al. 2020 Nat. Commun. 11 2172
Google Scholar
[4] Dakos V, Carpenter S R, Brock W A, et al. 2012 PLoS One 7 e41010
Google Scholar
[5] Carpenter S R, Brock W A 2006 Ecol. Lett. 9 311
Google Scholar
[6] Held H, Kleinen T 2004 Geophys. Res. Lett. 31 L23207
Google Scholar
[7] Boettiger C, Hastings A 2012 J. R. Soc. Interface. 9 2527
Google Scholar
[8] Scheffer M, Bascompte J, Brock W A, et al. 2009 Nature 461 53
Google Scholar
[9] Lade S J, Gross T 2012 PLoS Comput. Biol. 8 e1002360
Google Scholar
[10] Carpenter S R, Brock W A 2011 Ecology 92 2196
Google Scholar
[11] Bauch C T, Sigdel R, Pharaon J, Anand M 2016 Proc. Natl. Acad. Sci. U. S. A. 113 14560
Google Scholar
[12] 颜鹏程, 侯威, 胡经国 2012 物理学报 61 139202
Google Scholar
Yan P C, Hou W, Hu J G 2012 Acta Phys. Sin. 61 139202
Google Scholar
[13] 吴浩, 封国林, 侯威, 颜鹏程 2013 物理学报 62 059202
Google Scholar
Wu H, Feng G L, Hou W, Yan P C 2013 Acta Phys. Sin. 62 059202
Google Scholar
[14] 吴浩, 侯威, 颜鹏程, 封国林 2012 物理学报 61 209202
Google Scholar
Wu H, Hou W, Yan P C, Feng G L 2012 Acta Phys. Sin. 61 209202
Google Scholar
[15] Boers N 2018 Nat. Commun. 9 2556
Google Scholar
[16] Meisel C, Klaus A, Kuehn C, Plenz D 2015 PLoS Comput. Biol. 11 e1004097
Google Scholar
[17] Dakos V, Van Nes E H, D’Odorico P, Scheffer M 2012 Ecology 93 264
Google Scholar
[18] Kuznetsov Y A 2023 Elements of Applied Bifurcation Theory (Cham: Springer International Publishing) pp77–102
[19] Bury T M, Bauch C T, Anand M 2020 J. R. Soc. Interface 17 20200482
Google Scholar
[20] Chen Z, Fan P Y, Hou X T, Feng G L, Qian Z H 2024 Chaos Soliton. Fract. 187 115409
Google Scholar
[21] Gardiner C W 1985 Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Berlin: Springer) pp106–107
[22] Box G E, Jenkins G M, Reinsel G C, Ljung G M 2015 Time Series Analysis: Forecasting and Control (Hoboken: John Wiley & Sons) pp21–47
[23] Welch P 1967 IEEE Trans. Audio Electroacoustics 15 70
Google Scholar
[24] Prescott S A, De Koninck Y, Sejnowski T J 2008 PLoS Comput. Biol. 4 e1000198
Google Scholar
[25] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
Google Scholar
[26] Kendall M G 1938 Biometrika 30 81
Google Scholar
[27] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
Google Scholar
-
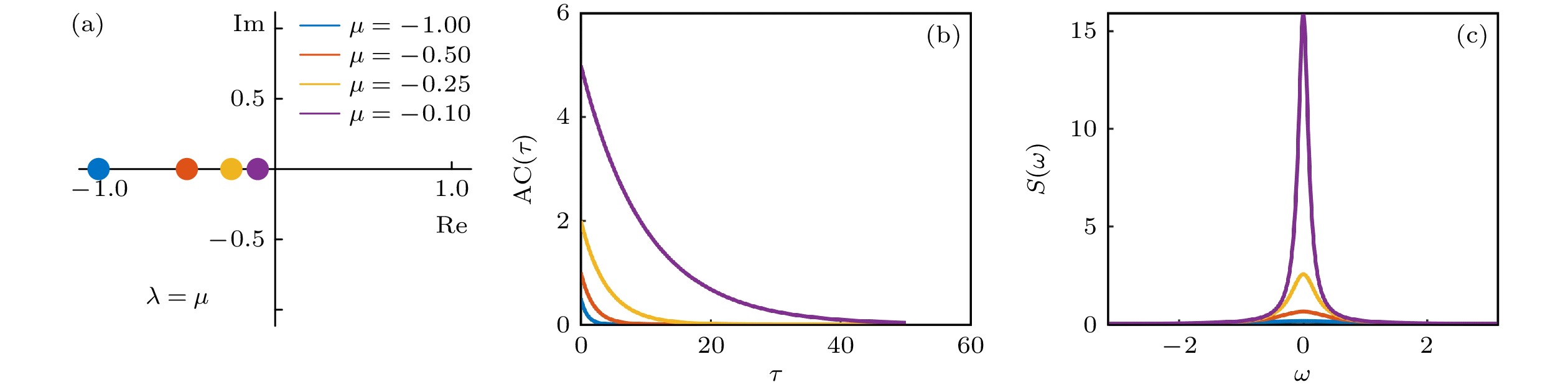
图 1 折叠分岔中自相关和功率谱的近似解析解 (a) 特征值趋近于0; (b) 不同特征值下, 自相关函数随时滞$\tau $的变化; (c) 不同特征值下功率谱的变化
Figure 1. Approximate analytic solutions for autocorrelation and power spectra in fold bifurcation: (a) The eigenvalue approaching to zero; (b) autocorrelation versus lag $\tau $ under different eigenvalues; (c) variation of power spectrum under different eigenvalues.
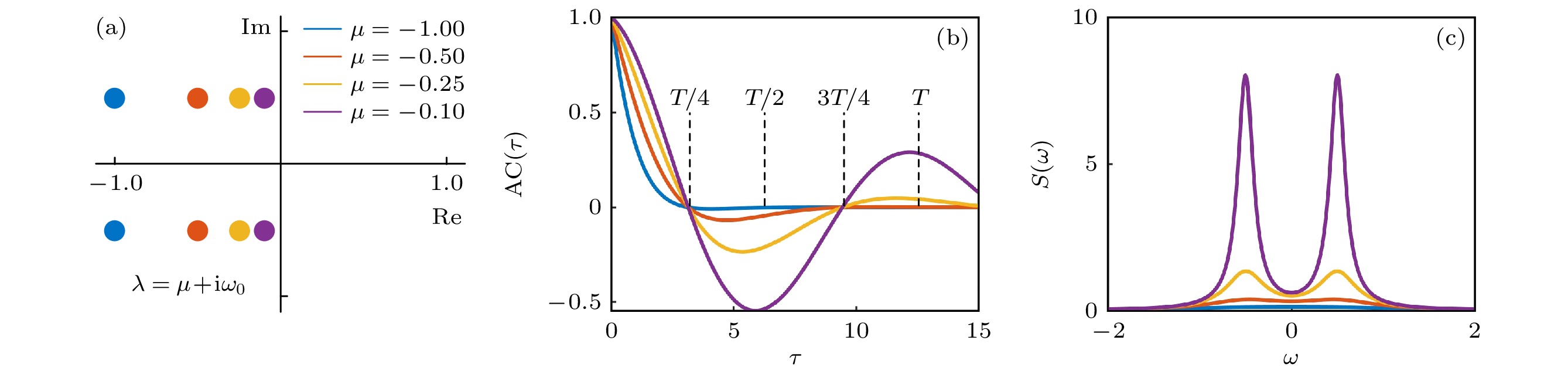
图 2 Hopf分岔中自相关和功率谱的近似解析解 (a) 特征值趋近于0; (b) 不同特征值下, 自相关函数随时滞$\tau $的变化; (c) 不同特征值下功率谱的变化
Figure 2. Approximate analytic solutions for autocorrelation and power spectra in Hopf bifurcation: (a) Real part of eigenvalues approaching to zero; (b) autocorrelation versus lag $\tau $ under different eigenvalues; (c) variation of power spectrum under different eigenvalues.
图 3 ML模型膜电位对外加电流的分岔图(SNIC)
Figure 3. Bifurcation diagram of membrane potential versus externally applied current in ML model (SNIC).
图 4 ML模型SNIC分岔前膜电位对增加的电流刺激的模拟响应
Figure 4. Simulated response of membrane potential versus increasing externally applied current on ML model before SNIC bifurcation.
图 5 ML模型SNIC分岔前的残差数据
Figure 5. Residual of ML model before SNIC bifurcation.
图 6 SNIC分岔的3种EWS随外加电流$I$的变化 (a) 时滞$\tau = 1$自相关系数随$I$变化; (b)方差随$I$变化; (c) ${S_{\max }}$随$I$变化
Figure 6. Three EWS’s on SNIC bifurcation versus externally applied current $I$: (a) Lag $\tau = 1$ autocorrelation versus $I$; (b) variance versus $I$; (c) ${S_{\max }}$ versus $I$.
图 7 ML模型SNIC分岔的功率谱 (a)不同外加电流$I$下的功率谱; (b) 功率谱等高线图
Figure 7. Power spectrum of the ML model before the SNIC bifurcation: (a) Power spectrum under different externally applied current $I$; (b) contour map of power spectrum.
图 8 ML模型膜电位对外加电流的分岔图(超临界Hopf)
Figure 8. Bifurcation diagram of membrane potential versus externally applied current in ML model (supercritical Hopf).
图 9 ML模型超临界Hopf分岔前膜电位对增大的电流刺激的模拟响应 (a) 原始序列; (b) 残差序列
Figure 9. Simulated response of membrane potential versus increasing externally applied current on ML model before supercritical Hopf bifurcation: (a) Original series; (b) residual series.
图 10 超临界Hopf分岔的3种EWS随外加电流$I$的变化 (a) 时滞$\tau = 1$自相关系数; (b)方差; (c) ${S_{\max }}$
Figure 10. Three EWS’s on supercritical hopf bifurcation versus externally applied current $I$: (a) Lag $\tau = 1$ autocorrelation; (b) variance; (c) ${S_{\max }}$.
图 11 ML模型超临界Hopf分岔的功率谱 (a)不同外加电流$I$下的功率谱; (b) 功率谱等高线图
Figure 11. Power spectrum of the ML model before the supercritical Hopf bifurcation: (a) Power spectrum under different externally applied current $I$; (b) contour map of power spectrum.
图 12 HR模型膜电位对外加电流的分岔图(鞍结分岔)
Figure 12. Bifurcation diagram of membrane potential versus externally applied current in HR model (saddle-node).
图 13 HR模型鞍结分岔前膜电位对增加的电流刺激的模拟响应 (a) 原始序列; (b) 残差序列
Figure 13. Simulated response of membrane potential versus increasing externally applied current on HR model before saddle-node bifurcation: (a) Original series; (b) residual series.
图 14 鞍结分岔的三种EWS随外加电流$I$的变化 (a) 时滞$\tau = 1$自相关系数; (b)方差; (c) ${S_{\max }}$
Figure 14. Three EWS’s on saddle-node bifurcation versus externally applied current $I$: (a) Lag $\tau = 1$ autocorrelation; (b) variance; (c) ${S_{\max }}$.
图 15 HR模型鞍结分岔的功率谱 (a)不同外加电流$I$下的功率谱; (b) 功率谱等高线图
Figure 15. Power spectrum of the HR model before the saddle-node bifurcation: (a) Power spectrum under different externally applied current $I$; (b) contour map of power spectrum.
图 16 HR模型膜电位对外加电流的分岔图(亚临界Hopf)
Figure 16. Bifurcation diagram of membrane potential versus externally applied current in HR model (subcritical Hopf).
图 17 HR模型亚临界Hopf分岔前膜电位对增加的电流刺激的模拟响应 (a) 原始序列; (b) 残差序列
Figure 17. Simulated response of membrane potential versus increasing externally applied current on HR model before subcritical Hopf bifurcation: (a) Original series; (b) residual series.
图 18 亚临界Hopf分岔的3种EWS随外加电流$I$的变化 (a) 时滞$\tau = 1$自相关系数; (b)方差; (c) ${S_{\max }}$
Figure 18. Three EWS’s on subcritical Hopf bifurcation versus externally applied current $I$: (a) Lag $\tau = 1$ autocorrelation; (b) variance; (c) ${S_{\max }}$.
图 19 HR模型亚临界Hopf分岔的功率谱 (a)不同外加电流$I$下的功率谱; (b) 功率谱等高线图
Figure 19. Power spectrum of the HR model before the subcritical Hopf bifurcation: (a) Power spectrum under different externally applied current $I$; (b) contour map of power spectrum.
-
[1] Grziwotz F, Chang C W, Dakos V, et al. 2023 Sci. Adv. 9 eabq4558
Google Scholar
[2] Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Boca Raton: CRC Press) pp70–80
[3] Maturana M I, Meisel C, Dell K, et al. 2020 Nat. Commun. 11 2172
Google Scholar
[4] Dakos V, Carpenter S R, Brock W A, et al. 2012 PLoS One 7 e41010
Google Scholar
[5] Carpenter S R, Brock W A 2006 Ecol. Lett. 9 311
Google Scholar
[6] Held H, Kleinen T 2004 Geophys. Res. Lett. 31 L23207
Google Scholar
[7] Boettiger C, Hastings A 2012 J. R. Soc. Interface. 9 2527
Google Scholar
[8] Scheffer M, Bascompte J, Brock W A, et al. 2009 Nature 461 53
Google Scholar
[9] Lade S J, Gross T 2012 PLoS Comput. Biol. 8 e1002360
Google Scholar
[10] Carpenter S R, Brock W A 2011 Ecology 92 2196
Google Scholar
[11] Bauch C T, Sigdel R, Pharaon J, Anand M 2016 Proc. Natl. Acad. Sci. U. S. A. 113 14560
Google Scholar
[12] 颜鹏程, 侯威, 胡经国 2012 物理学报 61 139202
Google Scholar
Yan P C, Hou W, Hu J G 2012 Acta Phys. Sin. 61 139202
Google Scholar
[13] 吴浩, 封国林, 侯威, 颜鹏程 2013 物理学报 62 059202
Google Scholar
Wu H, Feng G L, Hou W, Yan P C 2013 Acta Phys. Sin. 62 059202
Google Scholar
[14] 吴浩, 侯威, 颜鹏程, 封国林 2012 物理学报 61 209202
Google Scholar
Wu H, Hou W, Yan P C, Feng G L 2012 Acta Phys. Sin. 61 209202
Google Scholar
[15] Boers N 2018 Nat. Commun. 9 2556
Google Scholar
[16] Meisel C, Klaus A, Kuehn C, Plenz D 2015 PLoS Comput. Biol. 11 e1004097
Google Scholar
[17] Dakos V, Van Nes E H, D’Odorico P, Scheffer M 2012 Ecology 93 264
Google Scholar
[18] Kuznetsov Y A 2023 Elements of Applied Bifurcation Theory (Cham: Springer International Publishing) pp77–102
[19] Bury T M, Bauch C T, Anand M 2020 J. R. Soc. Interface 17 20200482
Google Scholar
[20] Chen Z, Fan P Y, Hou X T, Feng G L, Qian Z H 2024 Chaos Soliton. Fract. 187 115409
Google Scholar
[21] Gardiner C W 1985 Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Berlin: Springer) pp106–107
[22] Box G E, Jenkins G M, Reinsel G C, Ljung G M 2015 Time Series Analysis: Forecasting and Control (Hoboken: John Wiley & Sons) pp21–47
[23] Welch P 1967 IEEE Trans. Audio Electroacoustics 15 70
Google Scholar
[24] Prescott S A, De Koninck Y, Sejnowski T J 2008 PLoS Comput. Biol. 4 e1000198
Google Scholar
[25] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
Google Scholar
[26] Kendall M G 1938 Biometrika 30 81
Google Scholar
[27] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 498
- PDF Downloads: 22
- Cited By: 0
