-
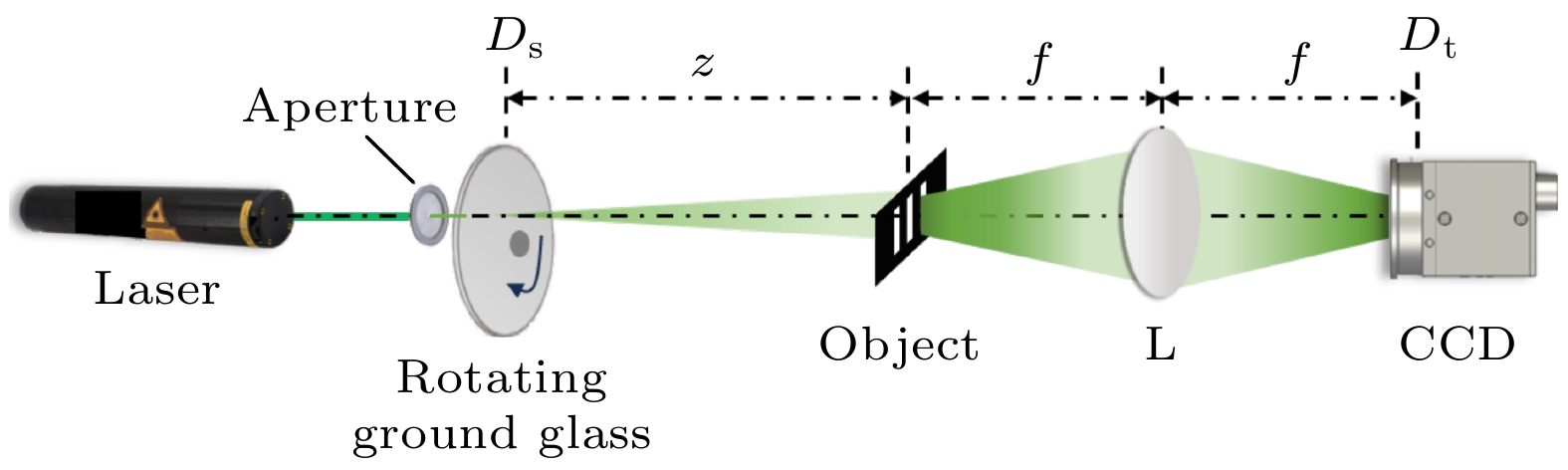
The second-order auto-correlation technology based on Hanbury Brown-Twiss (HBT) can obtain the Fourier spectrum information of a target even under the conditions of incoherent source illumination and near-field detection, which has better advantages in the fields of moving-target imaging, imaging in scattering medium, and X-ray imaging. However, a great number of measurements are required and the imaging resolution is also restricted by the pixel scale of the detector for high-quality Fourier spectrum image for HBT. At present, many relevant data processing methods and reconstruction algorithms can reduce the number of measurements required for the acquisition of high-quality spectral information, but the time of image reconstruction required by these methods is usually long and cannot improve the imaging resolution of the system. In recent years, Fourier ptychography based on real-space image detection has proven that higher-resolution imaging can be obtained through spectral ptychography and frequency extension. In this paper, by combining the idea of Fourier ptychography with HBT, a processing method based on multi-point parallel correlation reconstruction and spectral ptychography is proposed, which attempts to obtain high-quality spectral information of the target and achieve super-resolution imaging with few measurements. The proof-of-principle schematic of super-resolution imaging method based on autocorrelation and spectral ptychography is obtained. The corresponding super-resolution reconstruction framework is displayed, which mainly consists of three steps: multi-point parallel correlation reconstruction, spectral ptychography, and real-space image reconstruction based on phase-retrieval algorithm. Firstly, based on the physical mechanism, Fourier spectrum images of the target at different detection points are obtained through multi-point parallel correlation reconstruction. Secondly, according to the idea of spectrum ptychography, the frequency shifted spectrum obtained by multi-point parallel correlation reconstruction is aligned to form an extended spectrum. Finally, the target’s real-space image is reconstructed by phase-retrieval algorithm. The super-resolution imaging method based on auto-correlation and spectral ptychography is experimentally verified by using the setup. At the number of measurements N = 500, the experimental results are obtained on different pixel scales of the detector. The results indicate that the imaging resolution increases with the pixel scale of the detector increasing. However, when the number of measurements is small, both the Fourier spectrum and the real-space image obtained by single point detection are poor. When the multi-point parallel correlation reconstruction and spectral ptychography are adopted, the signal-to-noise ratio of the reconstructed Fourier spectrum can be significantly improved, and its spectral bandwidth can be expanded to twice that of the original spectrum at the same parameters. In addition, the experiments also show that for a 50×50 spectral image, even with 200 measurements (i.e. a sampling rate of 8%), high-quality super-resolution imaging can still be obtained. All in all, the proposed method provides important insights into super-resolution microscopy imaging and high-resolution imaging of moving target. -
Keywords:
- super-resolution imaging /
- auto-correlation /
- frequency ptychography /
- phase-retrieval algorithm
[1] Brown R H, Twiss R Q 1956 Nature 177 27
 Google Scholar
Google Scholar
[2] Glauber R J 1963 Phys. Rev. 130 2529
 Google Scholar
Google Scholar
[3] Zhang M H, Wei Q, Shen X, Liu Y F, Liu H L, Bai Y F, Han S S 2007 Phys. Lett. A 366 569
 Google Scholar
Google Scholar
[4] Gatti A, Bache M, Magatti D, Brambilla E, Ferri F, Lugiato L A 2006 J. Mod. Opt. 53 739
 Google Scholar
Google Scholar
[5] Shapiro J H, Boyd R W 2012 Quantum Inf. Process. 11 949
 Google Scholar
Google Scholar
[6] Shih Y H 2024 Chin. Opt. Lett. 22 060011
 Google Scholar
Google Scholar
[7] Zhao C Q, Gong W L, Chen M L, Li E R, Wang H, Xu W D, Han S S 2012 Appl. Phys. Lett. 101 141123
 Google Scholar
Google Scholar
[8] Erkmen B I. 2012 J. Opt. Soc. Am. A 29 782
 Google Scholar
Google Scholar
[9] Gong W L, Zhao C Q, Yu H, Chen M L, Xu W D, Han S S 2016 Sci. Rep. 6 26133
 Google Scholar
Google Scholar
[10] Stellinga D, Phillips D B, Mekhail S P, Selyem A, Turtaev S, Čižmár T, Padgett M J 2021 Science 374 1395
 Google Scholar
Google Scholar
[11] Sun Z, Tuitje F, Spielmann C 2019 Opt. Express 27 33652
 Google Scholar
Google Scholar
[12] Peng J Z, Yao M H, Huang Z B, Zhong J G 2021 APL Photonics 6 046102
 Google Scholar
Google Scholar
[13] Wu D X, Luo J W, Huang G Q, Feng Y H, Feng X H, Zhang R S, Shen Y C, Li Z H 2021 Nat. Commun. 12 4712
 Google Scholar
Google Scholar
[14] Ota S, Horisaki R, Kawamura Y, et al. 2018 Science 360 1246
 Google Scholar
Google Scholar
[15] Elser V 2003 J. Opt. Soc. Am. A 20 40
 Google Scholar
Google Scholar
[16] Ying G R, Wei Q, Shen X, Han S S 2008 Opt. Commun. 281 5130
 Google Scholar
Google Scholar
[17] Zhang C, Gong W L, Han S S 2013 Appl. Phys. Lett. 102 021111
 Google Scholar
Google Scholar
[18] Bo Z W, Gong W L, Han S S 2016 Chin. Opt. Lett. 14 070301
 Google Scholar
Google Scholar
[19] Katz O, Small E, Silberberg Y 2012 Nat. Photonics 6 549
 Google Scholar
Google Scholar
[20] Cheng J, Han S S 2004 Phys. Rev. Lett. 92 093903
 Google Scholar
Google Scholar
[21] Yu H, Lu R H, Han S S, Xie H L, Du G H, Xiao T Q, Zhu D M 2016 Phys. Rev. Lett. 117 113901
 Google Scholar
Google Scholar
[22] 林洁, 程静 2010 光学学报 30 2912
 Google Scholar
Google Scholar
Lin J, Cheng J 2010 Acta Opt. Sin. 30 2912
 Google Scholar
Google Scholar
[23] Lei Z, Wang C F, Zhang D W, Wang L X, Gong W L 2017 IEEE Photonics J. 9 1
[24] Wang H, Han S S 2012 Europhys. Lett. 98 24003
 Google Scholar
Google Scholar
[25] Zhu R G, Yu H, Tan Z J, Lu R H, Han S S, Huang Z F, Wang J 2020 Opt. Express 28 17556
 Google Scholar
Google Scholar
[26] Zheng G A, Horstmeyer R, Yang C H 2013 Nat. Photonics 7 739
 Google Scholar
Google Scholar
[27] 孙佳嵩, 张玉珍, 陈钱, 左超 2016 光学学报 36 1011005
 Google Scholar
Google Scholar
Sun J S, Zhang Y Z, Chen Q, Zuo C 2016 Acta Opt. Sin. 36 1011005
 Google Scholar
Google Scholar
[28] Liu H L, Cheng J, Han S S 2007 J. Appl. Phys. 102 103102
 Google Scholar
Google Scholar
[29] Loh N T D, Eisebitt S, Flewett S, Elser V 2010 Phys. Rev. E 82 061128
 Google Scholar
Google Scholar
-
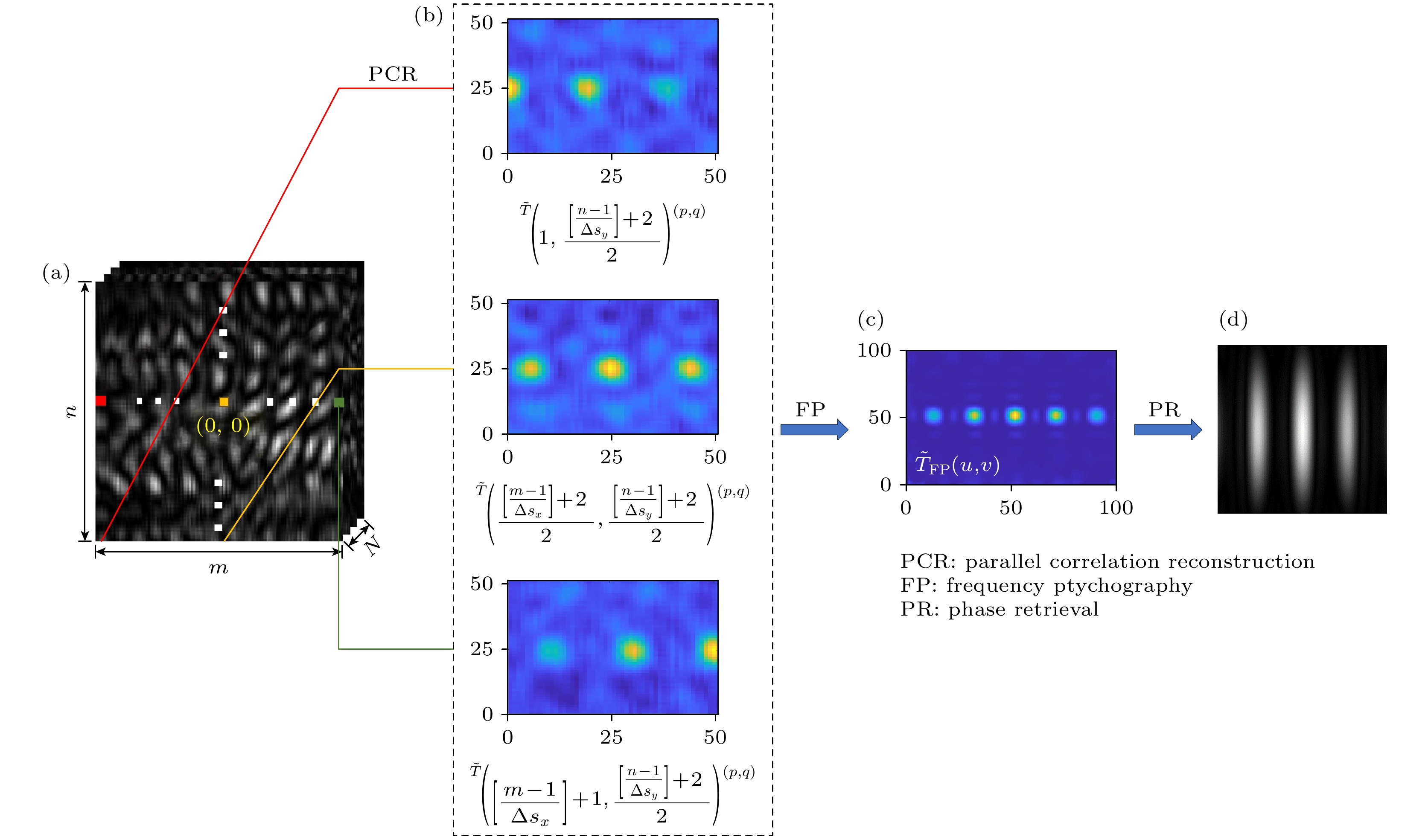
图 2 基于多点并行关联重建和频谱叠层处理实现超分辨重建的基本框架 (a) CCD记录的图片; (b)多点并行关联重建结果; (c)频域叠层结果; (d)基于相位恢复算法的实空间图像重建结果
Figure 2. The framework of super-resolution image reconstruction based on multiple-point parallel correlation reconstruction and frequency ptychography: (a) The recorded images recorded by CCD; (b) the results of multi-point parallel correlation algorithm; (c) the results of frequency ptychography; (d) the image in the spatial domain reconstructed by phase-retrieval algorithm.
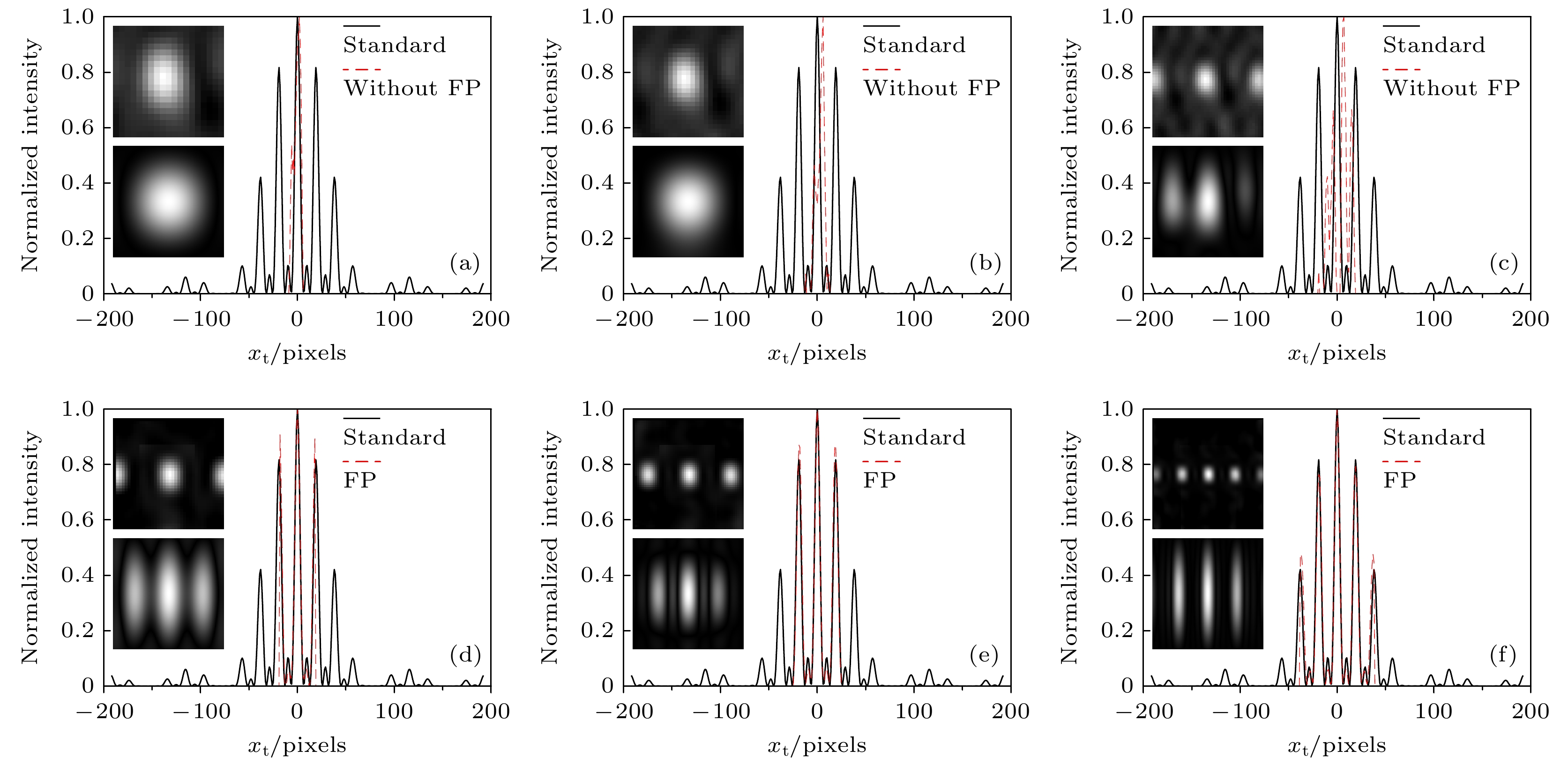
图 4 基于自相关和频谱叠层的超分辨成像实验验证结果(N = 500) (a)—(c)CCD像素规模大小分别为19×19, 25×25, 39×39像素不采用频谱叠层处理下的成像结果; (d)—(f)采用多点并行关联重建和频谱叠层处理后对应的成像结果, 左上角依次为关联重构的频谱图和相位恢复算法重建的实空间图像, 黑色实线为待测物体傅里叶变换频谱横截面, 红色虚线为关联重构频谱图的横截面
Figure 4. Experimental demonstration results of super-resolution imaging via autocorrelation and frequency ptychography (N = 500): (a)–(c) The imaging results without frequency ptychography when the pixel sizes of the CCD are 19×19, 25×25, and 39×39 pixels, respectively; (d)–(f) the corresponding results with multiple-point parallel correlation reconstruction and frequency ptychography. The upper left corner shows the frequency spectrums obtained by correlation reconstruction and the images in spatial domain reconstructed by phase-retrieval algorithm. The black solid line represents the cross-section of the testing object’s Fourier-transform spectrum, and the red dashed line represents the cross-section of the frequency spectrums obtained by correlation reconstruction.
图 5 不同测量次数下基于自相关和频谱叠层的成像结果(CCD像素规模大小为25×25像素) (a)多点并行关联重建和频谱叠层处理后的目标频谱图; (b)基于相位恢复算法重建的实空间图像
Figure 5. Imaging results based on autocorrelation and frequency ptychography in different measurements (with 25×25 pixels for the CCD): (a) The target’s frequency spectrum with multiple-point parallel correlation reconstruction and frequency ptychography; (b) the images in the spatial domain reconstructed by phase-retrieval algorithm.
-
[1] Brown R H, Twiss R Q 1956 Nature 177 27
 Google Scholar
Google Scholar
[2] Glauber R J 1963 Phys. Rev. 130 2529
 Google Scholar
Google Scholar
[3] Zhang M H, Wei Q, Shen X, Liu Y F, Liu H L, Bai Y F, Han S S 2007 Phys. Lett. A 366 569
 Google Scholar
Google Scholar
[4] Gatti A, Bache M, Magatti D, Brambilla E, Ferri F, Lugiato L A 2006 J. Mod. Opt. 53 739
 Google Scholar
Google Scholar
[5] Shapiro J H, Boyd R W 2012 Quantum Inf. Process. 11 949
 Google Scholar
Google Scholar
[6] Shih Y H 2024 Chin. Opt. Lett. 22 060011
 Google Scholar
Google Scholar
[7] Zhao C Q, Gong W L, Chen M L, Li E R, Wang H, Xu W D, Han S S 2012 Appl. Phys. Lett. 101 141123
 Google Scholar
Google Scholar
[8] Erkmen B I. 2012 J. Opt. Soc. Am. A 29 782
 Google Scholar
Google Scholar
[9] Gong W L, Zhao C Q, Yu H, Chen M L, Xu W D, Han S S 2016 Sci. Rep. 6 26133
 Google Scholar
Google Scholar
[10] Stellinga D, Phillips D B, Mekhail S P, Selyem A, Turtaev S, Čižmár T, Padgett M J 2021 Science 374 1395
 Google Scholar
Google Scholar
[11] Sun Z, Tuitje F, Spielmann C 2019 Opt. Express 27 33652
 Google Scholar
Google Scholar
[12] Peng J Z, Yao M H, Huang Z B, Zhong J G 2021 APL Photonics 6 046102
 Google Scholar
Google Scholar
[13] Wu D X, Luo J W, Huang G Q, Feng Y H, Feng X H, Zhang R S, Shen Y C, Li Z H 2021 Nat. Commun. 12 4712
 Google Scholar
Google Scholar
[14] Ota S, Horisaki R, Kawamura Y, et al. 2018 Science 360 1246
 Google Scholar
Google Scholar
[15] Elser V 2003 J. Opt. Soc. Am. A 20 40
 Google Scholar
Google Scholar
[16] Ying G R, Wei Q, Shen X, Han S S 2008 Opt. Commun. 281 5130
 Google Scholar
Google Scholar
[17] Zhang C, Gong W L, Han S S 2013 Appl. Phys. Lett. 102 021111
 Google Scholar
Google Scholar
[18] Bo Z W, Gong W L, Han S S 2016 Chin. Opt. Lett. 14 070301
 Google Scholar
Google Scholar
[19] Katz O, Small E, Silberberg Y 2012 Nat. Photonics 6 549
 Google Scholar
Google Scholar
[20] Cheng J, Han S S 2004 Phys. Rev. Lett. 92 093903
 Google Scholar
Google Scholar
[21] Yu H, Lu R H, Han S S, Xie H L, Du G H, Xiao T Q, Zhu D M 2016 Phys. Rev. Lett. 117 113901
 Google Scholar
Google Scholar
[22] 林洁, 程静 2010 光学学报 30 2912
 Google Scholar
Google Scholar
Lin J, Cheng J 2010 Acta Opt. Sin. 30 2912
 Google Scholar
Google Scholar
[23] Lei Z, Wang C F, Zhang D W, Wang L X, Gong W L 2017 IEEE Photonics J. 9 1
[24] Wang H, Han S S 2012 Europhys. Lett. 98 24003
 Google Scholar
Google Scholar
[25] Zhu R G, Yu H, Tan Z J, Lu R H, Han S S, Huang Z F, Wang J 2020 Opt. Express 28 17556
 Google Scholar
Google Scholar
[26] Zheng G A, Horstmeyer R, Yang C H 2013 Nat. Photonics 7 739
 Google Scholar
Google Scholar
[27] 孙佳嵩, 张玉珍, 陈钱, 左超 2016 光学学报 36 1011005
 Google Scholar
Google Scholar
Sun J S, Zhang Y Z, Chen Q, Zuo C 2016 Acta Opt. Sin. 36 1011005
 Google Scholar
Google Scholar
[28] Liu H L, Cheng J, Han S S 2007 J. Appl. Phys. 102 103102
 Google Scholar
Google Scholar
[29] Loh N T D, Eisebitt S, Flewett S, Elser V 2010 Phys. Rev. E 82 061128
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 2113
- PDF Downloads: 78
- Cited By: 0














 DownLoad:
DownLoad: