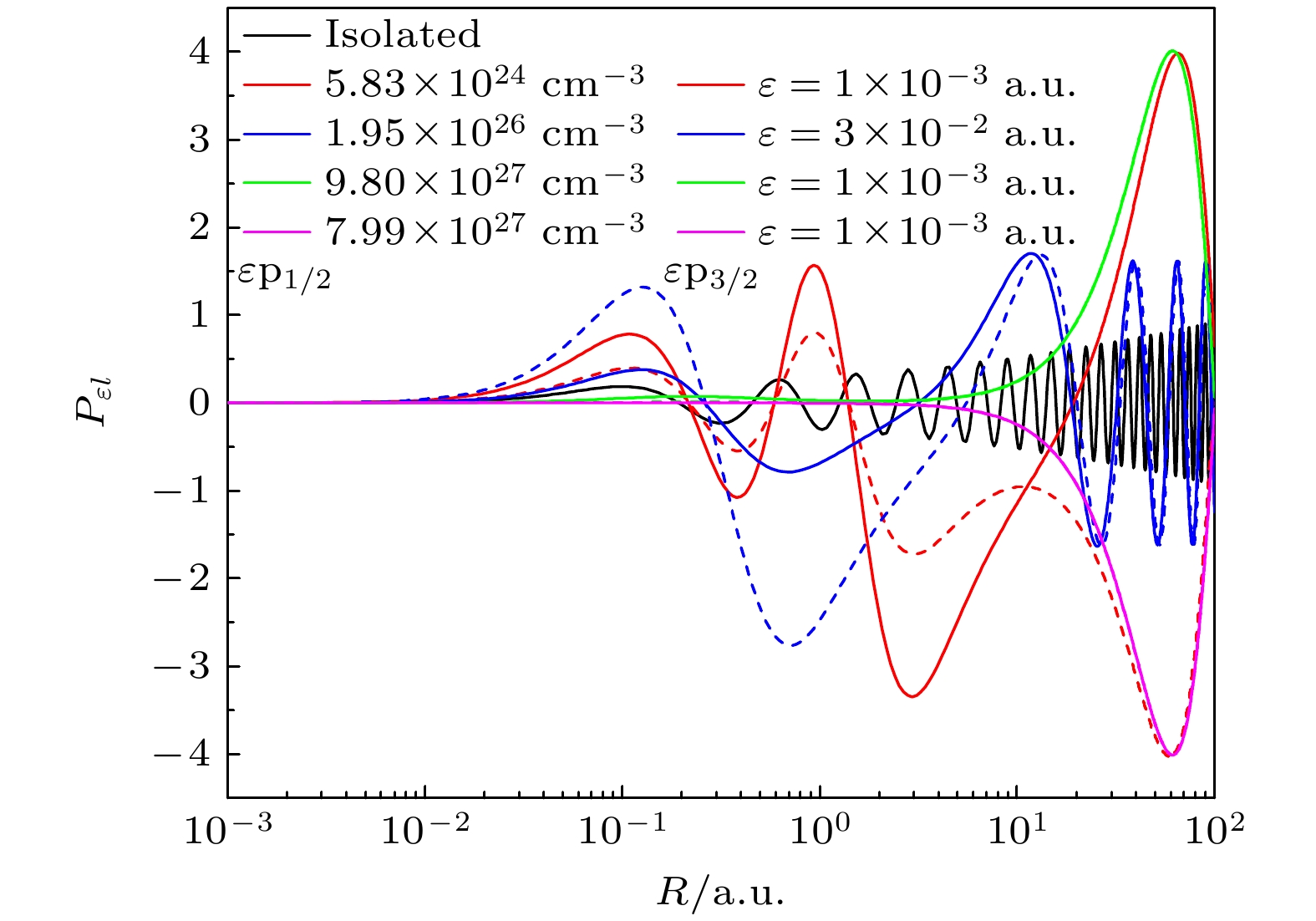
-
Complex multi-body interactions between ions and surrounding charged particles exist in hot and dense plasmas, and they can screen the Coulomb potential between the nucleus and electrons and significantly change the atomic structures and dynamic properties, thereby further affecting macroscopic plasma properties such as radiation opacity and the equation of state. Using the atomic-state-dependent (ASD) screening model, we investigate the photoionization dynamics of Fe25+ ions in hot and dense plasma. The photoionization cross section for all transition channels and total cross sections of n ≤ 2 states for Fe25+ ions are studied in detail, and the low-energy characteristics induced by plasma screening are also investigated. Compared with the classical Debye Hückel model, the ASD model introduces degeneracy effects through inelastic collision processes, resulting in higher plasma density requirements for bound electrons to merge into the continuum. Near the threshold, the photoionization cross section obeys the Wigner threshold law after considering the screening effect. As the energy increases, the cross sections show low-energy characteristics such as shape resonance, Cooper minimum, low-energy enhancement, and Combet-Farnoux minimum, which can significantly increase or reduce the cross section of the corresponding energy region. For example, the low-energy enhancement in the 2p→εs1/2 channel increases the cross section by several orders of magnitude, drastically changing the properties of the photoelectron spectrum. It is significant to study the low-energy characteristics for understanding the physical properties of the photoionization cross section. Fe is an important element in astrophysics. The cross section results in the medium and high energy regions calculated by the ASD model in this work can provide theoretical and data support for investigating hot and dense plasmas in astrophysics and laboratory.
[1] Astapenko V A, Lisitsa V S 2024 Matter Radiat. Extremes 9 057801
Google Scholar
[2] Alkhimova M, Skobelev I, Pikuz T, et al. 2024 Matter Radiat. Extremes 9 067205
Google Scholar
[3] Berrington K A, Burke P G, Butler K, Seaton M J, Storey P J, Taylor K T, Yan Y 1987 J. Phys. B: At. Mol. Phys. 20 6379
Google Scholar
[4] Hummer D G, Berrington K A, Eissner W, Pradhan A K, Saraph H E, Tully J A 1993 A& A 279 298
[5] Tong X M, Li J M, Pratt R H 1990 Phys. Rev. A 42 5348
Google Scholar
[6] Zhao L B, Ho Y K 2004 Phys. Plasmas 11 1695
Google Scholar
[7] Debye P, Hückel E 1923 Phys. Z. 24 185
[8] Salzmann D 1998 Atomic Physics in Hot Plasmas (Oxford: Oxford University Press
[9] Sahoo S, Ho Y K 2006 Phys. Plasmas 13 063301
Google Scholar
[10] Qi Y Y, Wang J G, Janev R K 2009 Phys. Rev. A 80 063404
Google Scholar
[11] Lin C Y, Ho Y K 2010 Phys. Plasmas 17 093302
Google Scholar
[12] Wu C S, Zhou F Y, Yan J, Gao X, Wu Y, Zeng C H, Wang J G 2024 Chin. Phys. Lett. 41 085202
Google Scholar
[13] Zhou F Y, Qu Y Z, Gao J W, Ma Y L, Wu Y, Wang J G 2021 Commun. Phys. 4 1
Google Scholar
[14] Lu S M, Zhou F Y, Xie L Y, Ma Y L, Zhao G P, Gao X, Wu Y, Wang J G 2024 Phys. Rev. E 109 055205
Google Scholar
[15] Ichimaru S 1982 Rev. Mod. Phys. 54 1017
Google Scholar
[16] https://www.nature.com/articles/s42005-021-00652-x [2025-1-1]
[17] Dyall K G, Grant I P, Johnson C T, Parpia F A, Plummer E P 1989 Comput. Phys. Commun. 55 425
Google Scholar
[18] Jönsson P, He X, Froese Fischer C, Grant I P 2007 Comput. Phys. Commun. 177 597
Google Scholar
[19] Tews M G, Perger W F 2001 Comput. Phys. Commun. 141 205
Google Scholar
[20] Perger W F, Halabuka Z, Trautmann D 1993 Comput. Phys. Commun. 76 250
Google Scholar
[21] Grant I P 1974 J. Phys. B: Aom. Molec. Phys. 7 1458
Google Scholar
[22] Zhao G P, Xie L Y, Liu L, Wang J G, Janev R K 2018 Phys. Plasmas 25 083302
Google Scholar
[23] Xie L Y, Wang J G, Janev R K 2014 Phys. Plasmas 21 063304
Google Scholar
[24] Bethe H A, Salpeter E E 1957 Quantum Mechanics of One- and Two-Electron Atoms (New York: Academic Press
[25] Fano U, Cooper J W 1968 Rev. Mod. Phys. 40 441
Google Scholar
[26] Wigner E P 1948 Phys. Rev. 73 1002
Google Scholar
[27] Bylicki M, Stachów A, Karwowski J, Mukherjee P K 2007 Chem. Phys. 331 346
Google Scholar
[28] Joachain 1975 Quantum Collision Theory (New York: American Elsevier
[29] Taylor J R 1972 Scattering Theory (New York: John Wiley
-
图 1 Fe25+离子基态的势能, Te = 200 eV, isolated表示孤立Fe25+离子的势能
Figure 1. Potential energy V(r) of Fe25+ ion at four electron densities ne and the temperature Te = 200 eV, the potential energy of the free Fe25+ ion is also plotted and represented as isolated.
图 2 采用ASD模型得到的εp1/2(实线), εp3/2(虚线)的连续波函数, Te = 200 eV
Figure 2. The radial wavefunction of εp1/2 (solid lines), εp3/2 (dashed lines) of continuous electrons from the ASD model, the electron temperature Te = 200 eV.
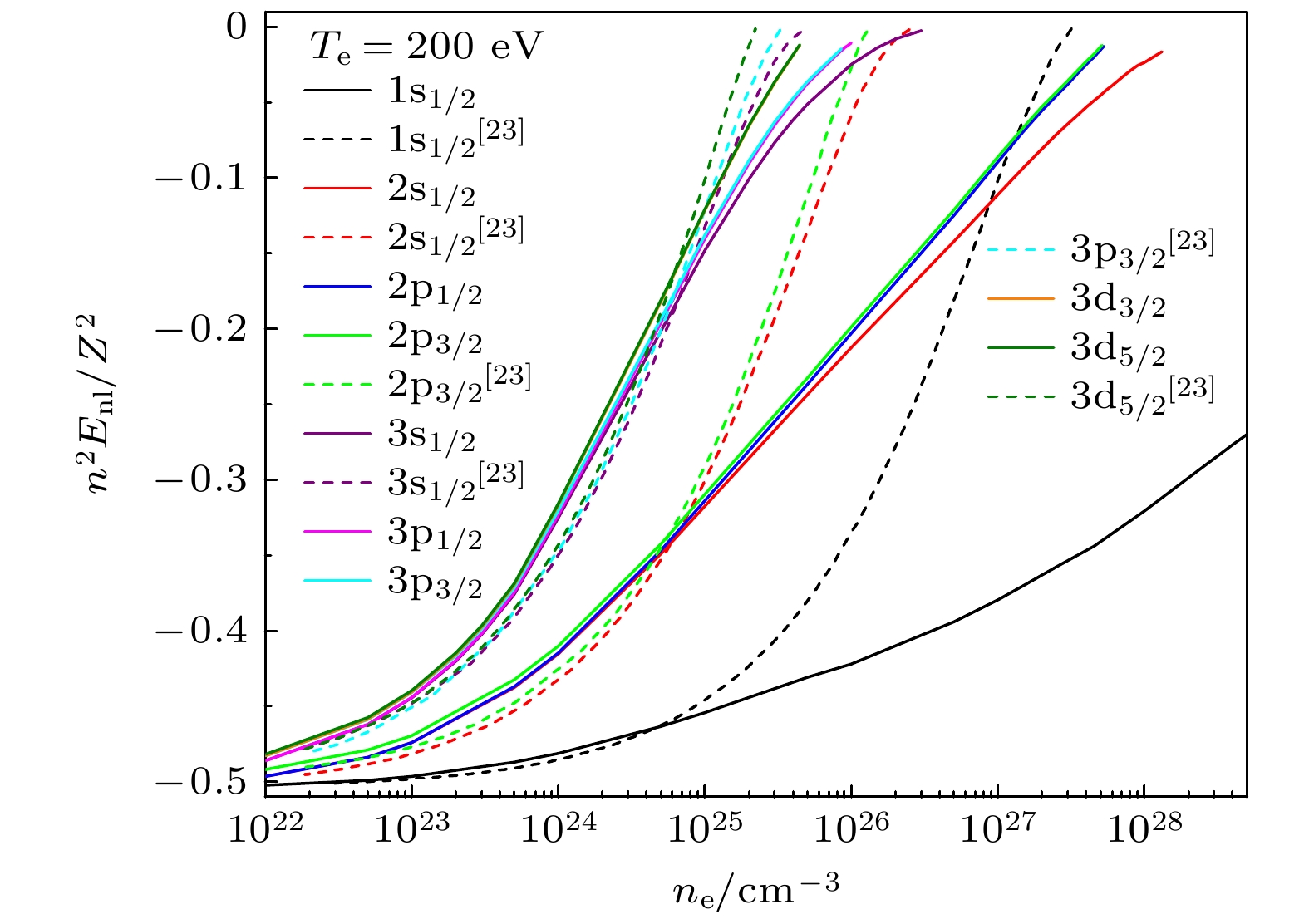
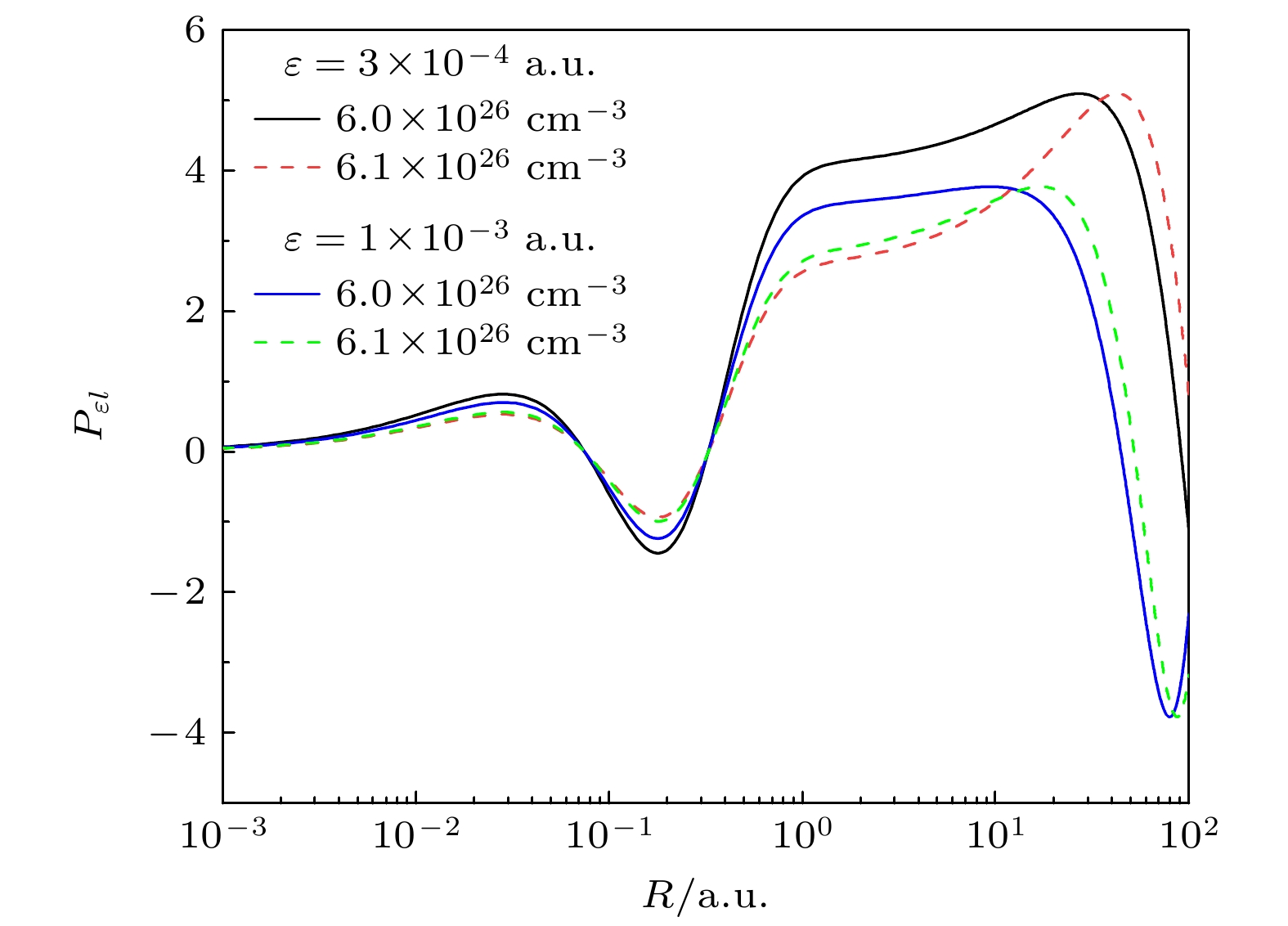
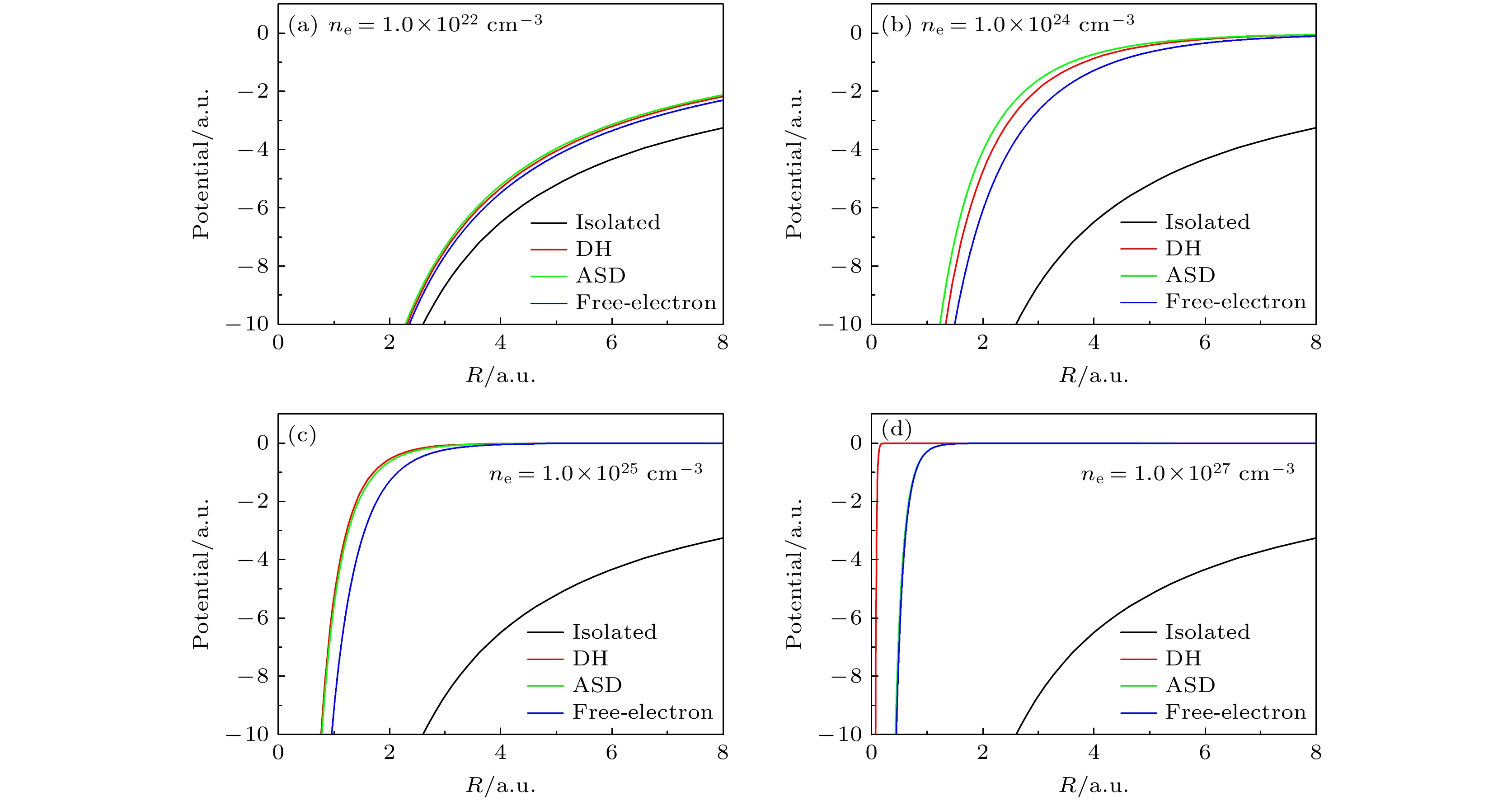
图 3 Fe25+离子基态及n ≤ 3激发态标度能级随电子密度的变化, 实线为ASD模型的结果, 虚线为Xie等[23]采用DH模型的计算结果
Figure 3. Scaled energies of ground and n ≤ 3 excited states of Fe25+ ion as a function of electron density for a fixed plasma temperature Te = 200 eV, the solid line is the result of ASD model, and the dotted line is the calculation result from DH model adopted by Xie et al.[23].
图 4 不同等离子体密度时Fe25+离子的基态光电离截面 (a) 1s总截面; (b) 1s→εp1/2; (c) 1s→εp3/2; 温度Te = 200 eV
Figure 4. Behavior of (a) total 1s, (b) individual 1s→εp1/2, and (c) 1s→εp3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
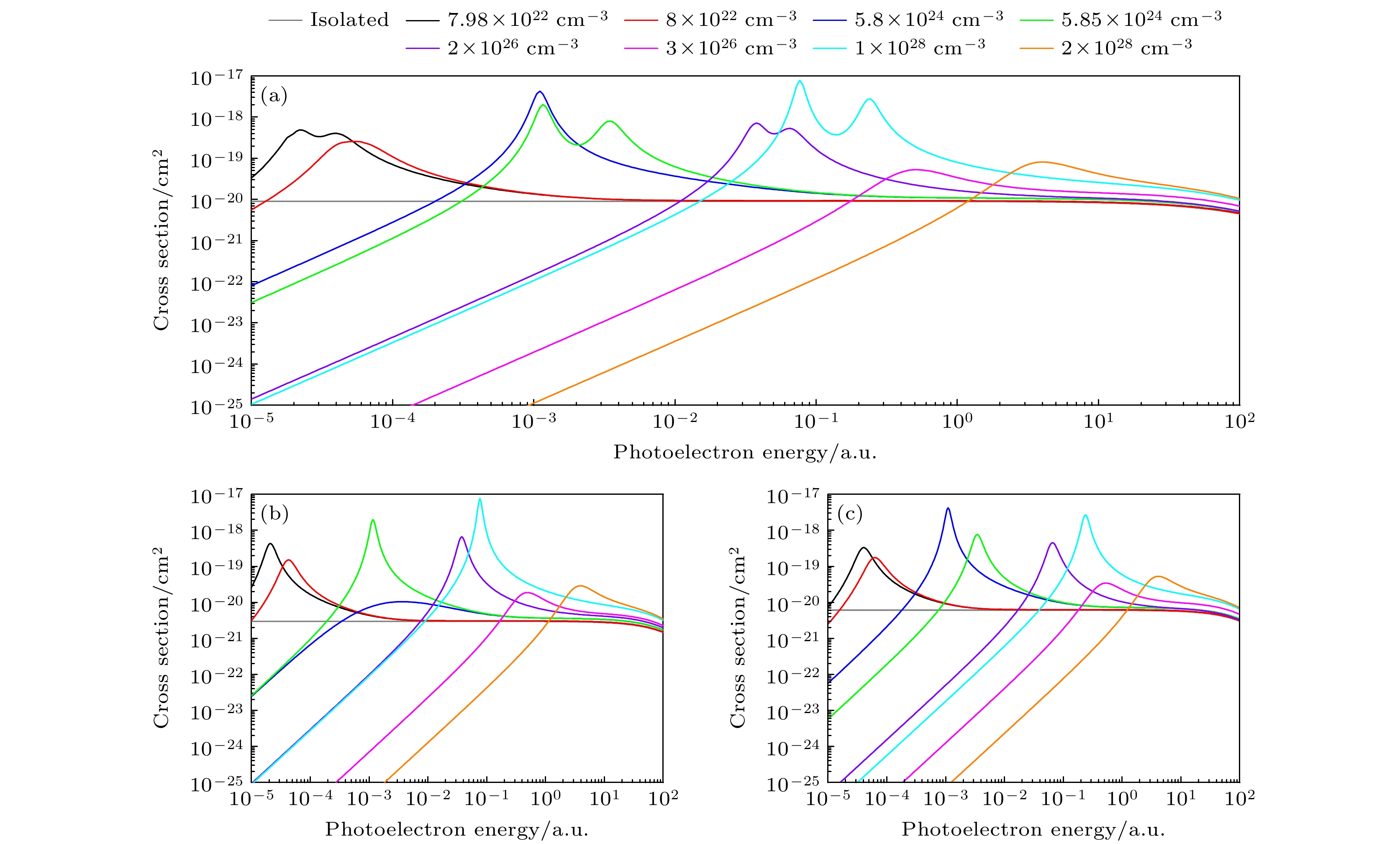
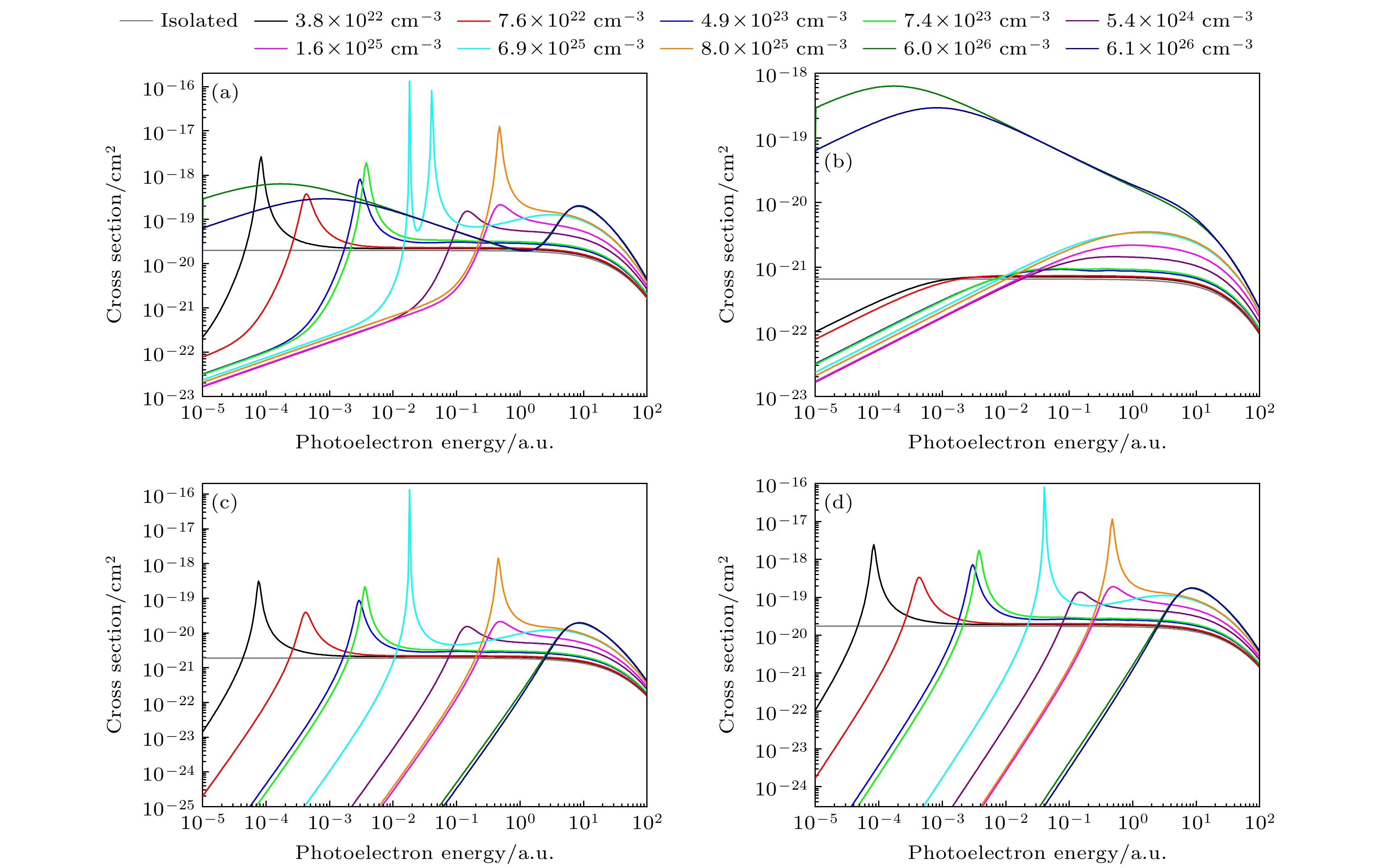
图 5 不同等离子体密度时Fe25+离子2s激发态的光电离截面 (a) 2s1/2总截面; (b) 2s1/2→εp1/2; (c) 2s1/2→εp3/2; 温度Te = 200 eV
Figure 5. Behavior of (a) total 2s1/2, (b) individual 2s1/2→εp1/2, and (c) 2s1/2→εp3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for a plasma with temperature Te = 200 eV.
图 6 Fe25+离子2s1/2激发态密度为 (a) 5.8×1024 cm–3, (b) 7.99×1027 cm–3和 (c) 9.8×1027 cm–3的偶极矩阵元, 温度Te = 200 eV
Figure 6. Dipole matrix elements of 2s1/2 excited state of Fe25+ ion with densities (a) 5.8×1024 cm–3, (b) 7.99×1027 cm–3, and (c) 9.8×1027 cm–3. Te = 200 eV.
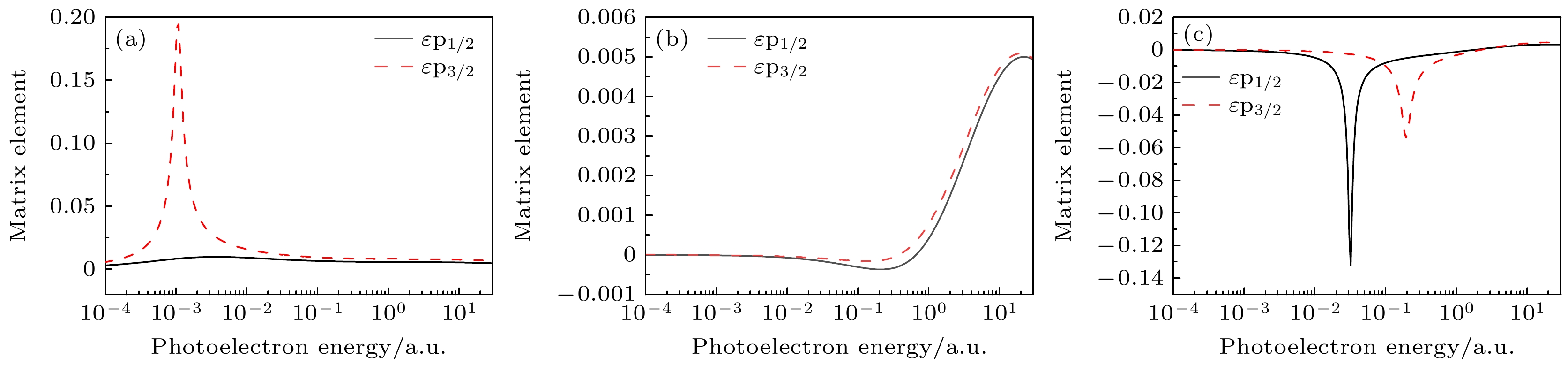
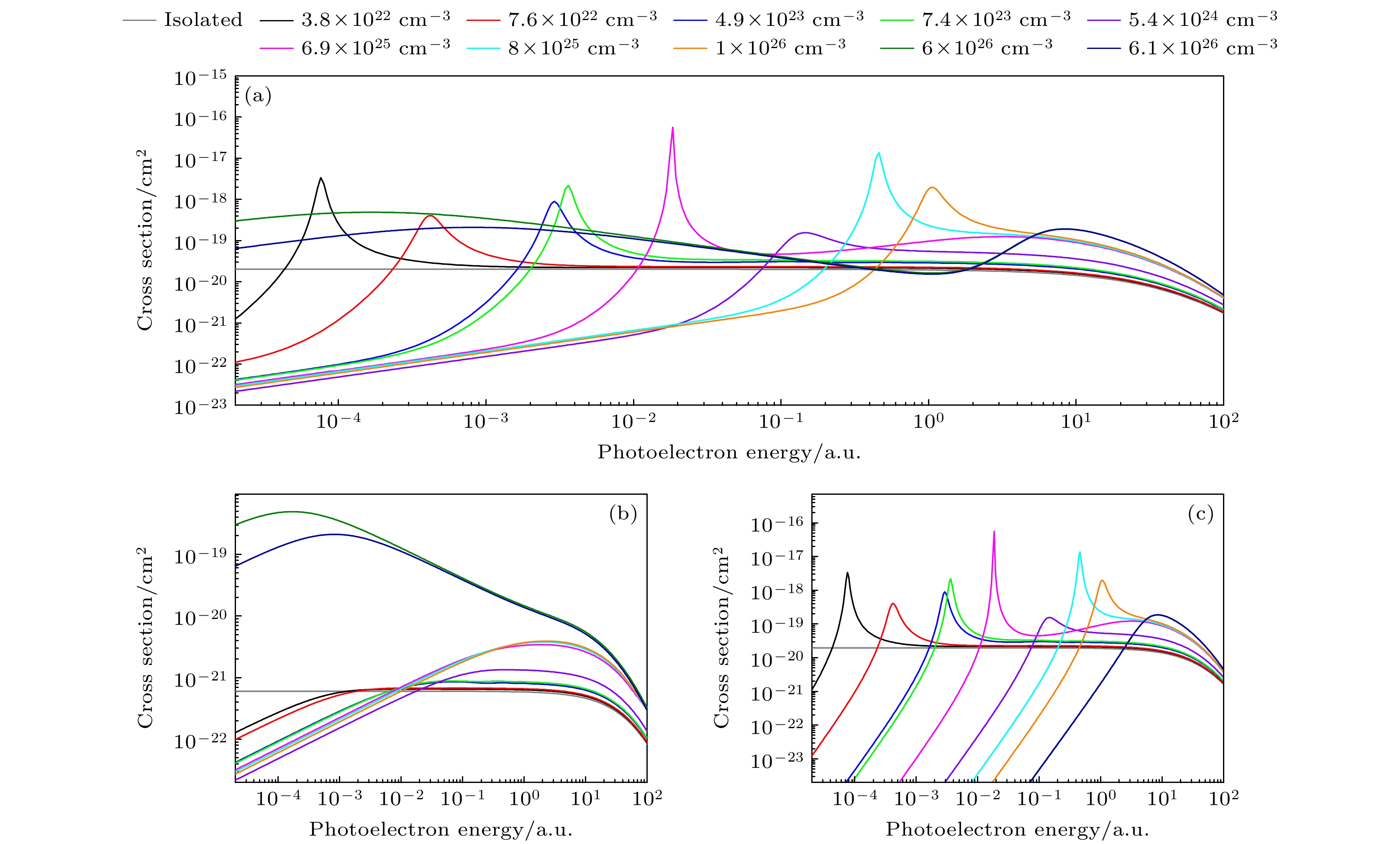
图 7 不同等离子体密度时Fe25+离子 (a) 2p1/2总截面, (b) 2p1/2→εs1/2截面以及(c) 2p1/2→εd3/2光电离截面, 温度Te = 200 eV
Figure 7. Behavior of (a) total 2p1/2, (b) individual 2p1/2→εs1/2, and (c) 2p1/2→εd3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
图 8 Fe25+离子εs1/2连续电子波函数的径向大分量, 温度Te = 200 eV
Figure 8. Large component of radial wavefunctions of εs1/2 continuous electron. Here the electron temperature is 200 eV.
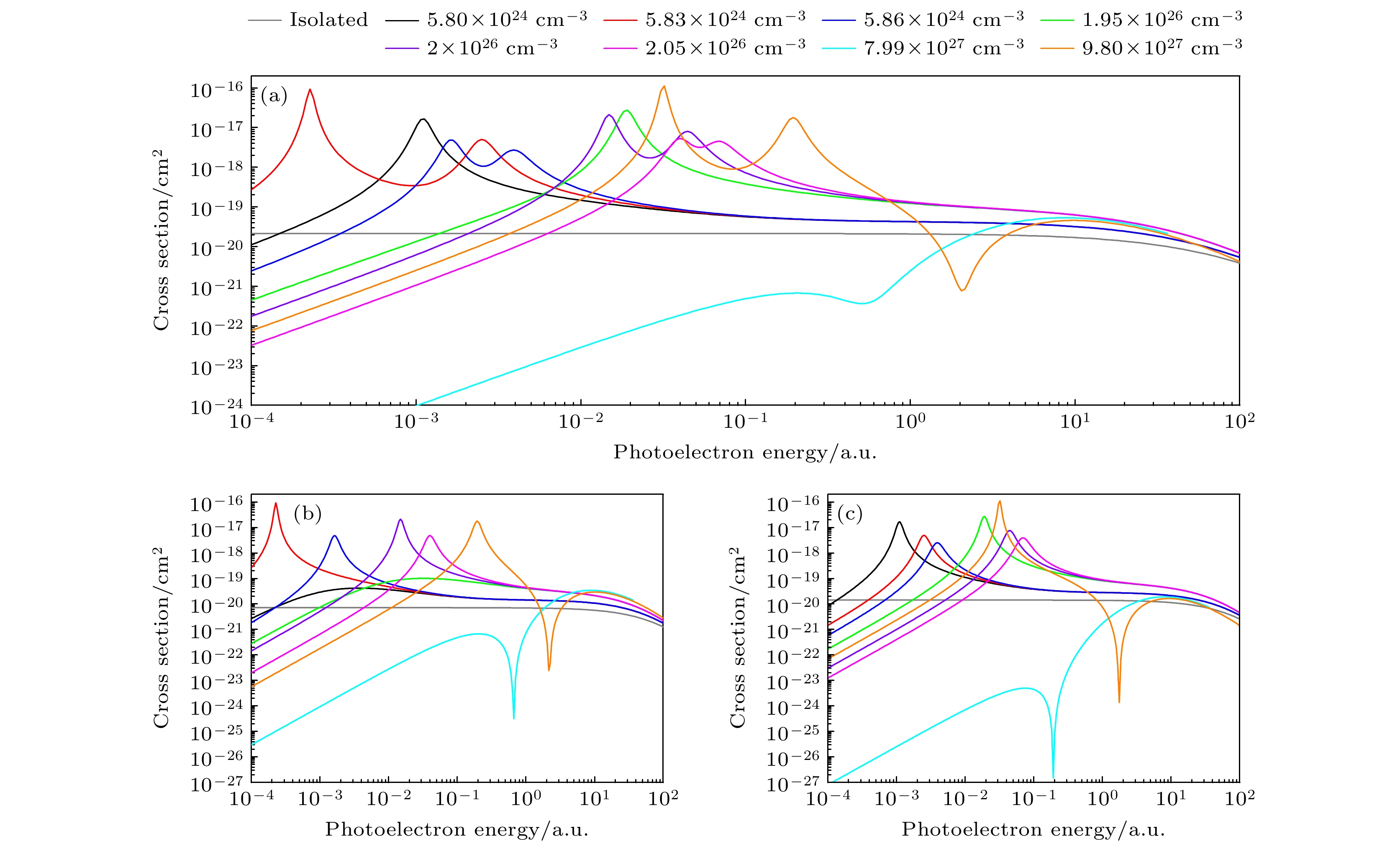
图 9 不同等离子体密度时Fe25+离子2p3/2激发态的光电离截面 (a) 2p3/2总截面; (b) 2p3/2→εs1/2; (c) 2p3/2→εd3/2; (d) 2p3/2→εd5/2; 温度Te = 200 eV
Figure 9. Behavior of (a) total 2p3/2, (b) individual 2p3/2→εs1/2, (c) 2p3/2→εd3/2, and (d) 2p3/2→εd5/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
-
[1] Astapenko V A, Lisitsa V S 2024 Matter Radiat. Extremes 9 057801
Google Scholar
[2] Alkhimova M, Skobelev I, Pikuz T, et al. 2024 Matter Radiat. Extremes 9 067205
Google Scholar
[3] Berrington K A, Burke P G, Butler K, Seaton M J, Storey P J, Taylor K T, Yan Y 1987 J. Phys. B: At. Mol. Phys. 20 6379
Google Scholar
[4] Hummer D G, Berrington K A, Eissner W, Pradhan A K, Saraph H E, Tully J A 1993 A& A 279 298
[5] Tong X M, Li J M, Pratt R H 1990 Phys. Rev. A 42 5348
Google Scholar
[6] Zhao L B, Ho Y K 2004 Phys. Plasmas 11 1695
Google Scholar
[7] Debye P, Hückel E 1923 Phys. Z. 24 185
[8] Salzmann D 1998 Atomic Physics in Hot Plasmas (Oxford: Oxford University Press
[9] Sahoo S, Ho Y K 2006 Phys. Plasmas 13 063301
Google Scholar
[10] Qi Y Y, Wang J G, Janev R K 2009 Phys. Rev. A 80 063404
Google Scholar
[11] Lin C Y, Ho Y K 2010 Phys. Plasmas 17 093302
Google Scholar
[12] Wu C S, Zhou F Y, Yan J, Gao X, Wu Y, Zeng C H, Wang J G 2024 Chin. Phys. Lett. 41 085202
Google Scholar
[13] Zhou F Y, Qu Y Z, Gao J W, Ma Y L, Wu Y, Wang J G 2021 Commun. Phys. 4 1
Google Scholar
[14] Lu S M, Zhou F Y, Xie L Y, Ma Y L, Zhao G P, Gao X, Wu Y, Wang J G 2024 Phys. Rev. E 109 055205
Google Scholar
[15] Ichimaru S 1982 Rev. Mod. Phys. 54 1017
Google Scholar
[16] https://www.nature.com/articles/s42005-021-00652-x [2025-1-1]
[17] Dyall K G, Grant I P, Johnson C T, Parpia F A, Plummer E P 1989 Comput. Phys. Commun. 55 425
Google Scholar
[18] Jönsson P, He X, Froese Fischer C, Grant I P 2007 Comput. Phys. Commun. 177 597
Google Scholar
[19] Tews M G, Perger W F 2001 Comput. Phys. Commun. 141 205
Google Scholar
[20] Perger W F, Halabuka Z, Trautmann D 1993 Comput. Phys. Commun. 76 250
Google Scholar
[21] Grant I P 1974 J. Phys. B: Aom. Molec. Phys. 7 1458
Google Scholar
[22] Zhao G P, Xie L Y, Liu L, Wang J G, Janev R K 2018 Phys. Plasmas 25 083302
Google Scholar
[23] Xie L Y, Wang J G, Janev R K 2014 Phys. Plasmas 21 063304
Google Scholar
[24] Bethe H A, Salpeter E E 1957 Quantum Mechanics of One- and Two-Electron Atoms (New York: Academic Press
[25] Fano U, Cooper J W 1968 Rev. Mod. Phys. 40 441
Google Scholar
[26] Wigner E P 1948 Phys. Rev. 73 1002
Google Scholar
[27] Bylicki M, Stachów A, Karwowski J, Mukherjee P K 2007 Chem. Phys. 331 346
Google Scholar
[28] Joachain 1975 Quantum Collision Theory (New York: American Elsevier
[29] Taylor J R 1972 Scattering Theory (New York: John Wiley
DownLoad:
Catalog
Metrics
- Abstract views: 553
- PDF Downloads: 30
- Cited By: 0
