-
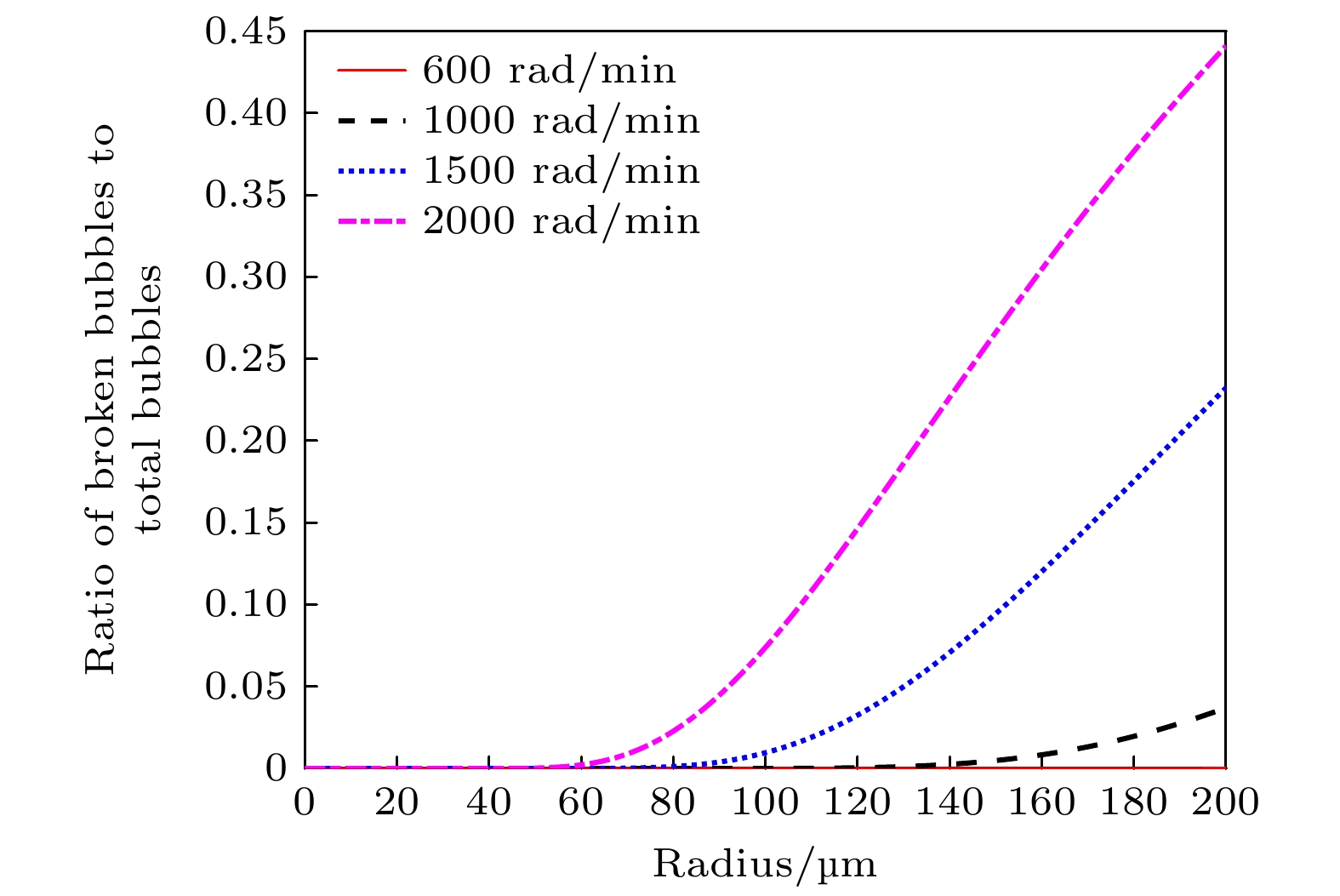
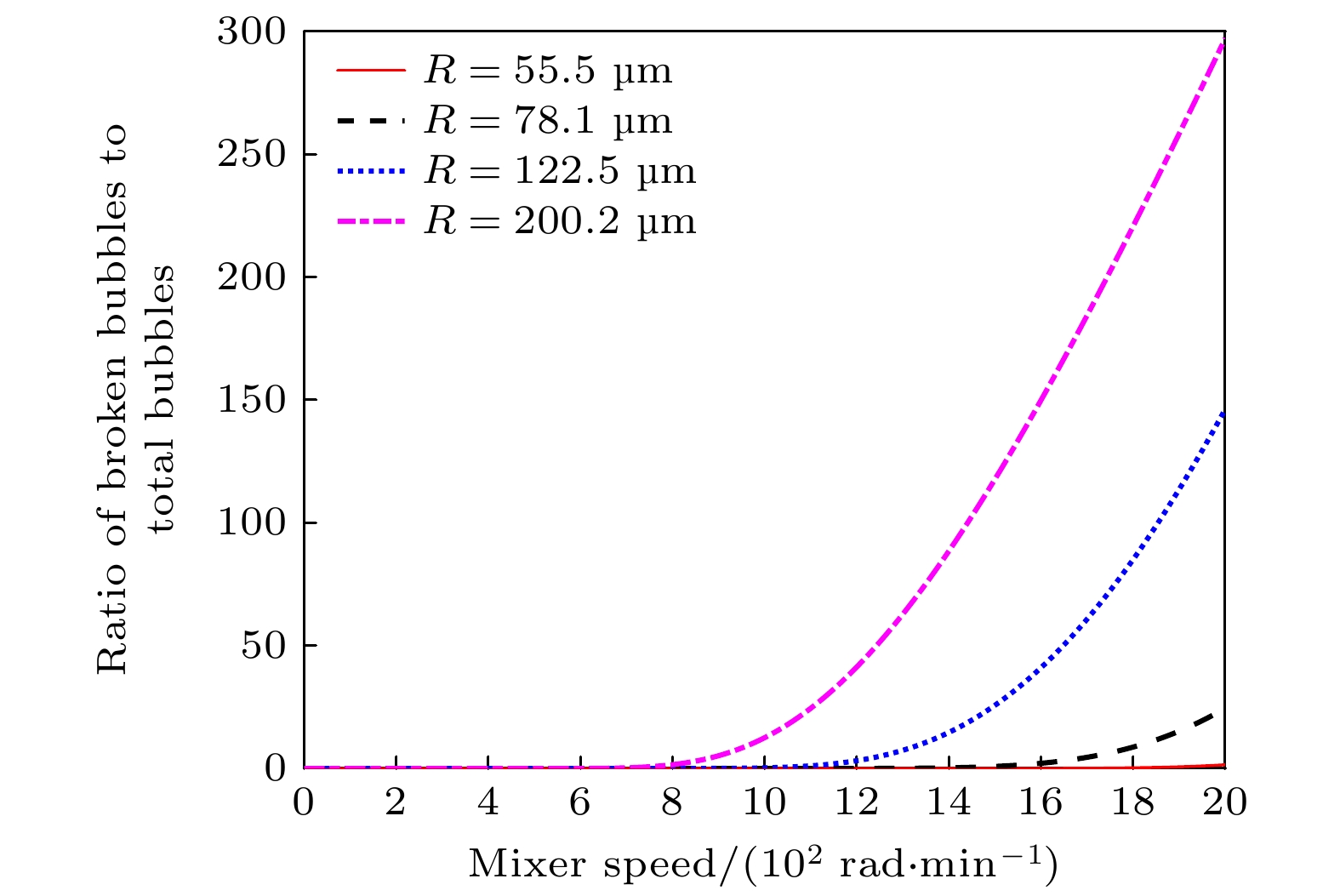
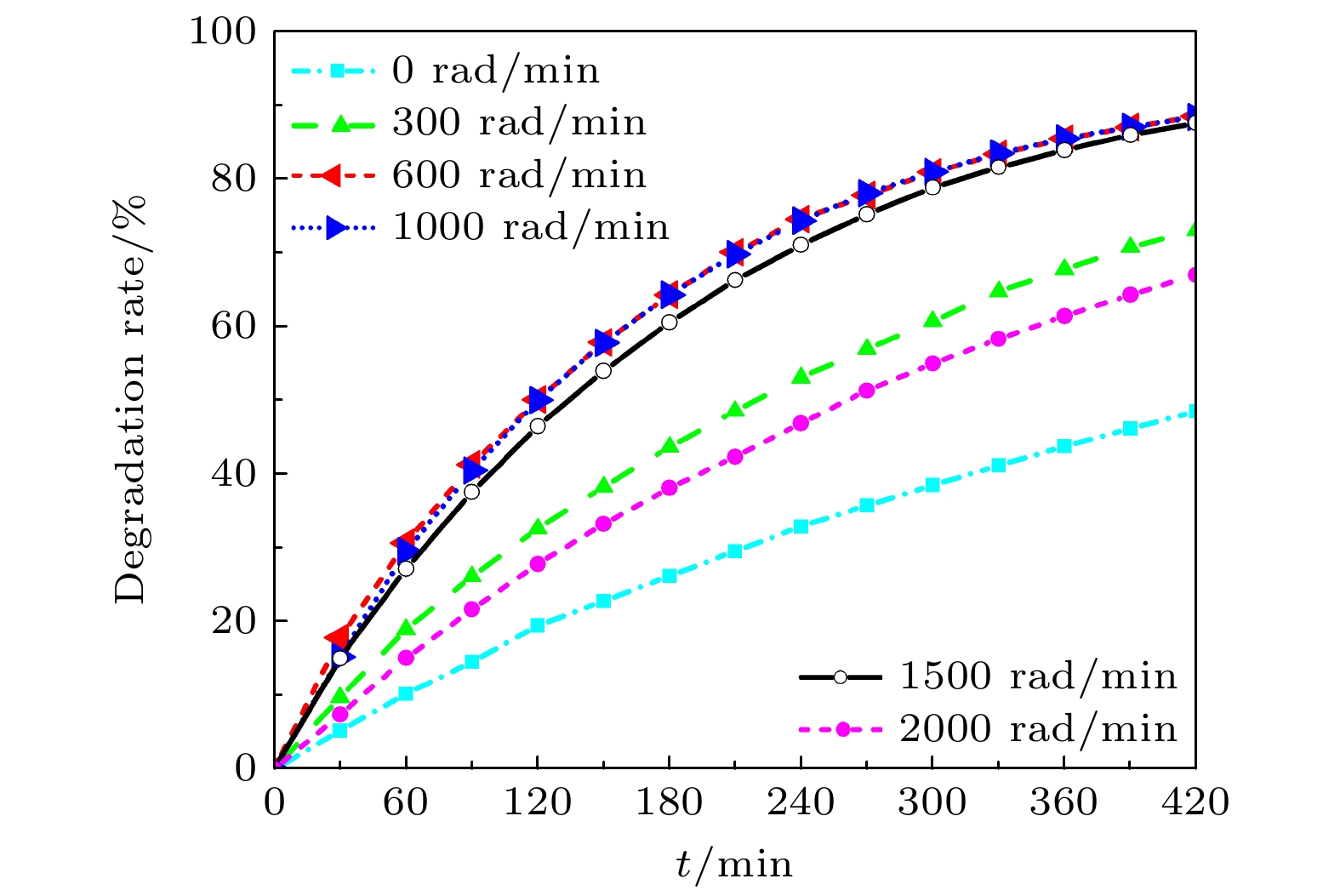
液态涡流场不仅可以传质传热影响声场分布, 还可以影响流场中气泡的行为特性, 进一步影响声空化效果. 以三维漏斗形涡流场中气泡的动力学方程并结合气泡破碎理论为基础, 研究了涡流场(搅拌产生的流场)对气泡破碎概率及其气泡空化效果的影响. 结果表明, 随着转速的增大, 气泡的破碎概率显著提高, 同时气泡破碎临界半径逐渐减小, 从600 rad/min时的200 μm降至2000 rad/min时的55.5 μm, 这意味着在高速旋转的涡流场中, 气泡在尚未膨胀到应达到的最大空化半径时就提前发生破碎, 导致其失去空化效应, 从而降低超声降解效果. 实验结果进一步验证了声空化效果在适中转速(600—1000 rad/min)下最佳, 而过高转速则会抑制降解效果. 这些发现为声空化技术的优化提供了理论基础和实验支持.
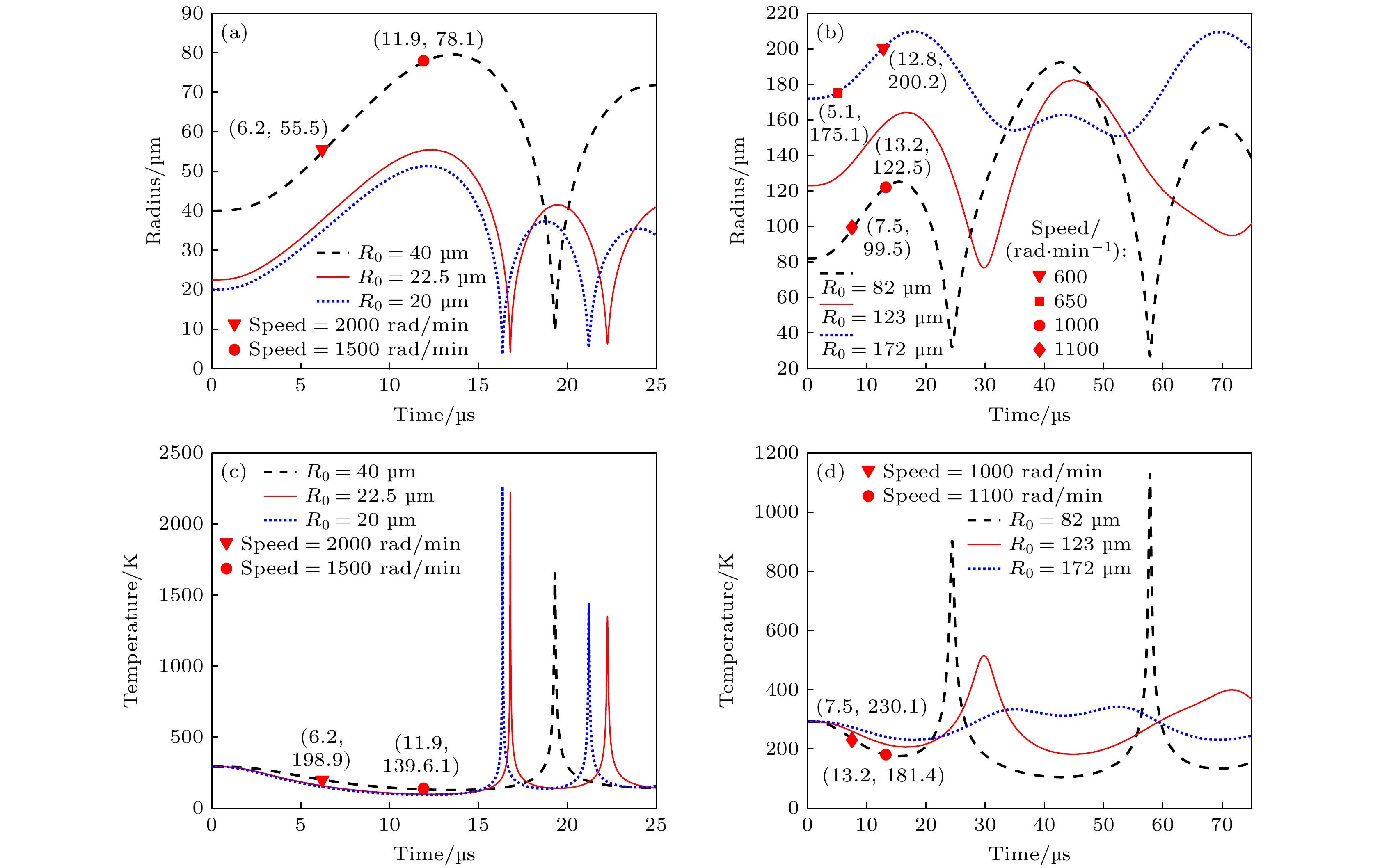
The liquid vortex flow field plays a crucial role not only in the transfer of matter and heat but also in significantly affecting the distribution of sound fields, which in turn influences the behavior of bubbles in the flow. This ultimately affects the phenomenon of acoustic cavitation. Based on the combination of the theory of bubble fragmentation and the theory of funnel-shaped vortex, in a three-dimensional vortex field. The effect of the vortex flow field (flow field generated by stirring) on the bubble breakup probability, as well as its modulation of acoustic cavitation, is investigated in this paper. In addition, the phenomena observed in experiments are explained. When the stirring speed reaches 1000 rad/min, the degradation effect no longer shows a monotonic increase, but instead begins to decline. It is demonstrated that with the increase of stirring speed, the probability of bubble breakup increases significantly. For instance, when the stirring speed is 1000 rad/min, the probability of bubble breakup is about 0.17%. At a stirring speed of 1500 rad/min, the breakup probability rises to 23%, and at 2000 rad/min, it reaches 44%. Moreover, the critical radius for bubble breakup decreases. The critical radius, as defined in this study, refers to the bubble radius at which the probability of breakup becomes nonzero. Experimental data show that at 600 rad/min, the critical radius for bubble breakup is about 200 μm, while at 2000 rad/min, it shortens to 55.5 μm. This indicates that in a high-speed rotating vortex field, bubbles may rupture before reaching their maximum cavitation radius, thus losing their effective cavitation effect. Further analysis shows that in the vortex flow field, for bubbles with an initial radius smaller than 22.5 μm, the temperature inside the bubbles upon collapse can reach as high as 2217.3 K (corresponding to an initial radius of 22.5 μm). For bubbles with an initial radius of 20 μm, the collapse temperature can even reach 2264.3 K. For bubbles with an initial radius of 40 μm, when the stirring speed does not exceed 1500 rad/min, the bubbles can still collapse under the action of the sound field, and the temperature inside the bubble upon collapse can reach 1659.6 K, which is sufficient to trigger off the cavitation effect. However, when the stirring speed exceeds 1500 rad/min, bubbles may break up too quickly and lose their cavitation capacity, thus failing to produce the expected cavitation effect. Experimental results further verify that at moderate stirring speeds (600—1000 rad/min), the acoustic cavitation effect is most pronounced, while excessively high stirring speeds suppress the enhancement of the degradation effect. This phenomenon suggests that the introduction of the vortex flow field makes the factors affecting acoustic cavitation more complex. The optimization of the acoustic cavitation effect requires not only the consideration of the sound field distribution and mass transfer but also the comprehensive factors such as gas entrainment, bubble aggregation, and breakup. Therefore, a thorough analysis and regulation of these factors are crucial for the widespread application of acoustic cavitation technology in engineering, with important theoretical value and practical significance, providing scientific basis and direction for further optimizing the acoustic cavitation process. -
Keywords:
- acoustic degradation /
- vortex field /
- bubble breakage /
- acoustic cavitation
[1] 宗星星 2023 现代工业经济和信息化 8 197
 Google Scholar
Google Scholar
Zong X X 2023 Mod. Ind. Econ. Inf. 8 197
 Google Scholar
Google Scholar
[2] Xu A, Wu Y H, Chen Z, Wu G, Wu Q, Ling F, Huang W E, Hu H Y 2020 Water Cycle 1 80
 Google Scholar
Google Scholar
[3] Khan N, Pu J Y, Pu C S, Xu H X, Gu X Y, Zhang L, Huang F F, Nasir M A, Ullah R 2019 Ultrason. Sonochem. 56 350
 Google Scholar
Google Scholar
[4] Dehghani M H, Karri R R, Koduru J R, Manickam S, Tyagi I, Mubarak N M, Suhasf 2023 Ultrason. Sonochem. 94 106302
 Google Scholar
Google Scholar
[5] Flores E M M, Cravotto G, Bizzi C A, Santos D, Iop G D 2021 Ultrason. Sonochem. 72 105455
 Google Scholar
Google Scholar
[6] Nanzai B, Mochizuki A, Wakikawa Y, Masuda Y, Oshio T, Yagishita K 2023 Ultrason. Sonochem. 95 106357
 Google Scholar
Google Scholar
[7] Pandit A V, Sarvothaman V P, Ranade V V 2021 Ultrason. Sonochem. 77 105677
 Google Scholar
Google Scholar
[8] Ji H F, Xu Y F, Shi H F, Yang X D 2024 Appl. Surf. Sci. 652 0169
 Google Scholar
Google Scholar
[9] Pokhrel N, Vabbina P K, Pala N 2016 Ultrason. Sonochem. 29 104
 Google Scholar
Google Scholar
[10] Tian S, Li B, Dai Y, Wang Z L 2023 Mater. Today. 68 254
 Google Scholar
Google Scholar
[11] Suslick K S, Price G J 1999 Annu. Rev. Mater. Sci. 29 295
 Google Scholar
Google Scholar
[12] 王双维, 冯若, 史群 1992 自然科学进展 3 267
Wang S W, Feng R, Shi Q 1992 Prog. Nat. Sci. 3 267
[13] Zhang Z B, Gao T, Liu X Y, Li D W, Zhao J, Lei Y, Wang Y K 2018 Ultrason. Sonochem. 42 787
 Google Scholar
Google Scholar
[14] Moholkar V S 2009 Chem. Eng. Sci. 64 5255
 Google Scholar
Google Scholar
[15] Ferkous H, Hamdaoui O, Pétrier C 2023 Ultrason. Sonochem. 99 106556
 Google Scholar
Google Scholar
[16] Wong C Y, Raymond J L, Usadi L N, Zong Z, Walton S C, Sedgwick A C, Kwan J 2023 Ultrason. Sonochem. 99 106559
 Google Scholar
Google Scholar
[17] Maghami S, Johansson Ö 2024 Ultrason. Sonochem. 103 106804
 Google Scholar
Google Scholar
[18] Zhang X G, Hao C C, Ma C, Shen Z Z, Guo J Z, Sun R G 2019 Ultrason. Sonochem. 58 104691
 Google Scholar
Google Scholar
[19] Madeleine J B, Zhang D K 2014 Ultrason. Sonochem. 21 485
 Google Scholar
Google Scholar
[20] Kojima Y, Asakura Y, Sugiyama G, Koda S 2010 Ultrason. Sonochem. 17 978
 Google Scholar
Google Scholar
[21] Liu J H, Shen Z Z, Lin S Y 2021 Phys. Rev. E 30 344
 Google Scholar
Google Scholar
[22] 魏鑫鑫 2022 硕士学位论文 (西安: 陕西师范大学)
Wei X X 2022 M. S. Thesis (Xi’an: Shaanxi Normal University
[23] 王英瑞 2022 硕士学位论文 (西安: 陕西师范大学)
Wang Y R 2018 M. S. Thesis (Xi’an: Shaanxi Normal University
[24] Choi J K, Chahine G 2003 Comput. Mech. 32 281
 Google Scholar
Google Scholar
[25] 陈云良, 伍超, 叶茂, 李静 2005 水利学报 36 1269
 Google Scholar
Google Scholar
Chen Y L, Wu C, Ye M, Li J 2005 J. Hydraul. Eng. 36 1269
 Google Scholar
Google Scholar
[26] Mih W C 2010 J. Hydraul. Res. 27 417
[27] Hasan B O 2017 Chin. J. Chem. Eng. 25 698
 Google Scholar
Google Scholar
[28] Coolaloglou C, Tavlarides L 1977 Chem. Eng. Sci 32 1289
 Google Scholar
Google Scholar
[29] Hasan B O, Hamad M F, Majdi H S, Hathal M M 2021 Eur. J. Mech. B/Fluids 85 430
 Google Scholar
Google Scholar
[30] 陈志希, 谢明辉, 周国忠, 虞培清, 王抚华 2010 化学工程 38 38
Chen Z X, Xie M H, Zhou G Z, Yu P Q, Wang F H 2010 Chem. Eng. J. 38 38
[31] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
 Google Scholar
Google Scholar
[32] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 76 046309.
 Google Scholar
Google Scholar
[33] 刘金河, 沈壮志, 林书玉 2021 物理学报 70 224301
 Google Scholar
Google Scholar
Liu J H, Shen Z Z, Lin S Y 2021 Acta Phys. Sin. 70 224301
 Google Scholar
Google Scholar
[34] Yusof N S M, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
 Google Scholar
Google Scholar
[35] Song K, Liu Y J, Ahmad U, Ma H L, Wang H X 2024 Chemosphere 350 141024
 Google Scholar
Google Scholar
[36] Lee D Y, Kang J, Son Y G 2023 Ultrason. Sonochem. 101 1350
 Google Scholar
Google Scholar
-
图 4 涡流场中声空化泡的破碎特性 (a) 1500 rad/min, 2000 rad/min转速下不同初始半径气泡破碎示意图; (b) 1000 rad/min, 1100 rad/min转速下不同初始半径气泡破碎示意图; (c) 1500 rad/min, 2000 rad/min转速下不同初始半径气泡破碎温度示意图; (d) 1000 rad/min, 1100 rad/min转速下不同初始半径气泡破碎温度示意图
Fig. 4. Fragmentation characteristics of cavitation bubbles in a turbulent flow field: (a) Schematic diagram of bubble fragmentation with different initial radii at 1500 rad/min and 2000 rad/min speeds; (b) schematic diagram of bubble fragmentation with different initial radii at speeds of 1000 rad/min and 1100 rad/min; (c) schematic diagram of bubble fragmentation temperature at different initial radii at 1500 rad/min and 2000 rad/min speeds; (d) schematic diagram of bubble fragmentation temperature at different initial radii at speeds of 1000 rad/min and 1100 rad/min.
表 1 不同搅拌转速对应的气泡破碎半径
Table 1. Bubble fragmentation radius corresponding to different stirring speeds.
搅拌转速/
(rad·min–1)破碎
半径/μm搅拌转速/
(rad·min–1)破碎
半径/μm500 251.1 1200 90.6 600 200.2 1300 85.4 700 175.1 1400 82.5 800 159.3 1500 78.0 900 136.6 1600 71.5 1000 122.1 1800 62.4 1100 99.5 2000 55.5 -
[1] 宗星星 2023 现代工业经济和信息化 8 197
 Google Scholar
Google Scholar
Zong X X 2023 Mod. Ind. Econ. Inf. 8 197
 Google Scholar
Google Scholar
[2] Xu A, Wu Y H, Chen Z, Wu G, Wu Q, Ling F, Huang W E, Hu H Y 2020 Water Cycle 1 80
 Google Scholar
Google Scholar
[3] Khan N, Pu J Y, Pu C S, Xu H X, Gu X Y, Zhang L, Huang F F, Nasir M A, Ullah R 2019 Ultrason. Sonochem. 56 350
 Google Scholar
Google Scholar
[4] Dehghani M H, Karri R R, Koduru J R, Manickam S, Tyagi I, Mubarak N M, Suhasf 2023 Ultrason. Sonochem. 94 106302
 Google Scholar
Google Scholar
[5] Flores E M M, Cravotto G, Bizzi C A, Santos D, Iop G D 2021 Ultrason. Sonochem. 72 105455
 Google Scholar
Google Scholar
[6] Nanzai B, Mochizuki A, Wakikawa Y, Masuda Y, Oshio T, Yagishita K 2023 Ultrason. Sonochem. 95 106357
 Google Scholar
Google Scholar
[7] Pandit A V, Sarvothaman V P, Ranade V V 2021 Ultrason. Sonochem. 77 105677
 Google Scholar
Google Scholar
[8] Ji H F, Xu Y F, Shi H F, Yang X D 2024 Appl. Surf. Sci. 652 0169
 Google Scholar
Google Scholar
[9] Pokhrel N, Vabbina P K, Pala N 2016 Ultrason. Sonochem. 29 104
 Google Scholar
Google Scholar
[10] Tian S, Li B, Dai Y, Wang Z L 2023 Mater. Today. 68 254
 Google Scholar
Google Scholar
[11] Suslick K S, Price G J 1999 Annu. Rev. Mater. Sci. 29 295
 Google Scholar
Google Scholar
[12] 王双维, 冯若, 史群 1992 自然科学进展 3 267
Wang S W, Feng R, Shi Q 1992 Prog. Nat. Sci. 3 267
[13] Zhang Z B, Gao T, Liu X Y, Li D W, Zhao J, Lei Y, Wang Y K 2018 Ultrason. Sonochem. 42 787
 Google Scholar
Google Scholar
[14] Moholkar V S 2009 Chem. Eng. Sci. 64 5255
 Google Scholar
Google Scholar
[15] Ferkous H, Hamdaoui O, Pétrier C 2023 Ultrason. Sonochem. 99 106556
 Google Scholar
Google Scholar
[16] Wong C Y, Raymond J L, Usadi L N, Zong Z, Walton S C, Sedgwick A C, Kwan J 2023 Ultrason. Sonochem. 99 106559
 Google Scholar
Google Scholar
[17] Maghami S, Johansson Ö 2024 Ultrason. Sonochem. 103 106804
 Google Scholar
Google Scholar
[18] Zhang X G, Hao C C, Ma C, Shen Z Z, Guo J Z, Sun R G 2019 Ultrason. Sonochem. 58 104691
 Google Scholar
Google Scholar
[19] Madeleine J B, Zhang D K 2014 Ultrason. Sonochem. 21 485
 Google Scholar
Google Scholar
[20] Kojima Y, Asakura Y, Sugiyama G, Koda S 2010 Ultrason. Sonochem. 17 978
 Google Scholar
Google Scholar
[21] Liu J H, Shen Z Z, Lin S Y 2021 Phys. Rev. E 30 344
 Google Scholar
Google Scholar
[22] 魏鑫鑫 2022 硕士学位论文 (西安: 陕西师范大学)
Wei X X 2022 M. S. Thesis (Xi’an: Shaanxi Normal University
[23] 王英瑞 2022 硕士学位论文 (西安: 陕西师范大学)
Wang Y R 2018 M. S. Thesis (Xi’an: Shaanxi Normal University
[24] Choi J K, Chahine G 2003 Comput. Mech. 32 281
 Google Scholar
Google Scholar
[25] 陈云良, 伍超, 叶茂, 李静 2005 水利学报 36 1269
 Google Scholar
Google Scholar
Chen Y L, Wu C, Ye M, Li J 2005 J. Hydraul. Eng. 36 1269
 Google Scholar
Google Scholar
[26] Mih W C 2010 J. Hydraul. Res. 27 417
[27] Hasan B O 2017 Chin. J. Chem. Eng. 25 698
 Google Scholar
Google Scholar
[28] Coolaloglou C, Tavlarides L 1977 Chem. Eng. Sci 32 1289
 Google Scholar
Google Scholar
[29] Hasan B O, Hamad M F, Majdi H S, Hathal M M 2021 Eur. J. Mech. B/Fluids 85 430
 Google Scholar
Google Scholar
[30] 陈志希, 谢明辉, 周国忠, 虞培清, 王抚华 2010 化学工程 38 38
Chen Z X, Xie M H, Zhou G Z, Yu P Q, Wang F H 2010 Chem. Eng. J. 38 38
[31] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
 Google Scholar
Google Scholar
[32] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 76 046309.
 Google Scholar
Google Scholar
[33] 刘金河, 沈壮志, 林书玉 2021 物理学报 70 224301
 Google Scholar
Google Scholar
Liu J H, Shen Z Z, Lin S Y 2021 Acta Phys. Sin. 70 224301
 Google Scholar
Google Scholar
[34] Yusof N S M, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
 Google Scholar
Google Scholar
[35] Song K, Liu Y J, Ahmad U, Ma H L, Wang H X 2024 Chemosphere 350 141024
 Google Scholar
Google Scholar
[36] Lee D Y, Kang J, Son Y G 2023 Ultrason. Sonochem. 101 1350
 Google Scholar
Google Scholar
计量
- 文章访问数: 3417
- PDF下载量: 81
- 被引次数: 0













 下载:
下载: