-
Quantum memories are indispensable for quantum communication and quantum computation, which are able to realize the storage and retrieval of a quantum state such as a single photon, entanglement, or a squeezed state on demand. Among those memories realized by different protocols, the Raman quantum memory has advantages in its broadband and high-speed properties, resulting in huge potential applications in quantum network and quantum computation. However, the realization of Raman quantum memory for a true single photon and photonic entanglement is a challenging job. In this review, after briefly introducing the main benchmarks for quantum memories, showing the state of the art, we focus on the review of the experimental progress recently achieved in storing the quantum state by Raman scheme in our group. We believe that all achievements reviewed are very hopeful in building up a high-speed quantum network.
-
Keywords:
- quantum storage /
- quantum information
[1] Sangouard N, Simon C, Zhao B, Chen Y A, de Riedmatten H, Pan J W, Gisin N 2008 Phys. Rev. A 77 062301
 Google Scholar
Google Scholar
[2] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
 Google Scholar
Google Scholar
[3] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
 Google Scholar
Google Scholar
[4] Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O'Brien J L 2010 Nature 464 54
 Google Scholar
Google Scholar
[5] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photon. 5 222
 Google Scholar
Google Scholar
[6] Majumdar A, Bajcsy M, Rundquist A, Vučković J 2012 Phys. Rev. Lett. 108 183601
 Google Scholar
Google Scholar
[7] Bussières F, Sangouard N, Afzelius M, de Riedmatten H, Simon C, Tittel W 2013 J. Mod. Opt. 60 1519
 Google Scholar
Google Scholar
[8] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
 Google Scholar
Google Scholar
[9] Radnaev A G, Dudin Y O, Zhao R, Jen H H, Jenkins S D, Kuzmich A, Kennedy T A B 2010 Nat. Phys. 6 894
 Google Scholar
Google Scholar
[10] Albrecht B, Farrera P, Gonzalvo X F, Cristiani M, de Riedmatten H 2014 Nat. Commun. 5 3376
 Google Scholar
Google Scholar
[11] Clausen C, Usmani I, Bussières F, Sangouard N, Afzelius M, de Riedmatten H, Gisin N 2011 Nature 469 508
 Google Scholar
Google Scholar
[12] Saglamyurek E, Sinclair N, Jin J, Slater J A, Oblak D, Bussières F, George M, Ricken R, Sohler W, Tittel W 2011 Nature 469 512
 Google Scholar
Google Scholar
[13] Simon C, de Riedmatten H, Afzelius M, Sangouard N, Zbinden H, Gisin N 2007 Phys. Rev. Lett. 98 190503
 Google Scholar
Google Scholar
[14] Zhang W, Ding D S, Shi S, Li Y, Zhou Z Y, Shi B S, Guo G C 2016 Phys. Rev. A 93 022316
 Google Scholar
Google Scholar
[15] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
 Google Scholar
Google Scholar
[16] Olmschenk S, Matsukevich D N, Maunz P, Hayes D, Duan L M, Monroe C 2009 Science 323 486
 Google Scholar
Google Scholar
[17] Kurz C, Schug M, Eich P, Huwer J, Müller P, Eschner J 2014 Nat. Commun. 5 5527
 Google Scholar
Google Scholar
[18] Togan E, Chu Y, Trifonov A S, Jiang L, Maze J, Childress L, Dutt M V G, Sørensen A S, Hemmer P R, Zibrov A S, Lukin M D 2010 Nature 466 730
 Google Scholar
Google Scholar
[19] Bernien H, Hensen B, Pfaff W, Koolstra G, Blok M S, Robledo L, Taminiau T H, Markham M, Twitchen D J, Childress L, Hanson R 2013 Nature 497 86
 Google Scholar
Google Scholar
[20] Greve D G, Yu L, McMahon P L, Pelc J S, Natarajan C M, Kim N Y, Abe E, Maier S, Schneider C, Kamp M, Höfling S, Hadfield R H, Forchel A, Fejer M M, Yamamoto Y 2012 Nature 491 421
 Google Scholar
Google Scholar
[21] Wang Q, Zhang Y S 2012 Eur. Phys. J. B 85 225
 Google Scholar
Google Scholar
[22] Dudin Y O, Li L, Kuzmich A 2013 Phys. Rev. A 87 031801
 Google Scholar
Google Scholar
[23] Xu Z X, Wu Y L, Tian L, Chen L, Zhang Z Y, Yan Z H, Li S J, Wang H, Xie C D, Peng K C 2013 Phys. Rev. Lett. 111 240503
 Google Scholar
Google Scholar
[24] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y H, Chen Y F, Yu I A, Chen Y C 2018 Phys. Rev. Lett. 120 183602
 Google Scholar
Google Scholar
[25] Zhou S, Zhang S C, Liu C, Chen J F, Wen J M, Loy M M T, Wong G K L, Du S W 2012 Opt. Express. 20 24124
 Google Scholar
Google Scholar
[26] Li J F, Wang Y F, Zhang S C, He J Y, Cheng A Q, Yan H, Zhu S L 2017 arXiv: 1706.01404[quant-ph]
[27] Ding D S, Zhou Z Y, Shi B S, Guo G C 2013 Nat. Commun. 4 2527
 Google Scholar
Google Scholar
[28] Ding D S, Zhang W, Zhou Z Y, Shi S, Pan J S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2014 Phys. Rev. A 90 042301
 Google Scholar
Google Scholar
[29] Ding D S, Zhang W, Zhou Z Y, Shi S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2015 Phys. Rev. Lett. 114 050502
 Google Scholar
Google Scholar
[30] Ding D S, Zhang W, Shi S, Zhou Z Y, Li Y, Shi B S, Guo G C 2016 Light: Science and Applications 5 e 5 e16157
 Google Scholar
Google Scholar
[31] Shi B S, Ding D S, Zhang W 2018 J. Phys. B: At. Mol. Opt. Phys. 51 032004
 Google Scholar
Google Scholar
[32] Hosseini M, Sparkes B M, Campbell G, Lam P K, Buchler B C 2011 Nat. Commun. 2 174
 Google Scholar
Google Scholar
[33] Higginbottom D B, Sparkes B M, Rancic M, Pinel O, Hosseini M, Lam P K, Buchler B C 2012 Phys. Rev. A 86 023801
 Google Scholar
Google Scholar
[34] Glorieux Q, Clark J B, Marino A M, Zhou Z F, Lett P D 2012 Opt. Express 20 12350
 Google Scholar
Google Scholar
[35] Shi S, Ding D S, Zhang W, Zhou Z Y, Dong M X, Liu S L, Wang K, Shi B S, Guo G C 2017 Phys. Rev. A 95 033823
 Google Scholar
Google Scholar
[36] Ding D S, Wu J H, Zhou Z Y, Liu Y, Shi B S, Zou X B, Guo G C 2013 Phys. Rev. A 87 013835
 Google Scholar
Google Scholar
[37] Zhong M J, Hedges M P, Ahlefeldt R L, Bartholomew J G, Beavan S E, Wittig S M, Longdell J J, Sellars M J 2015 Nature 517 177
 Google Scholar
Google Scholar
[38] Tang, J S, Zhou Z Q, Wang Y T, Li Y L, Liu X, Hua Y L, Zou Y, Wang S, He D Y, Chen G, Sun Y N, Yu Y, Li M F, Zha Z G, Ni H Q, Niu Z C, Li C F, Guo G C 2015 Nat. Commun. 6 8652
 Google Scholar
Google Scholar
[39] Sinclair N, Saglamyurek E, Mallahzadeh H, Slater J A., George M, Ricken R, Hedges M P, Oblak D, Simon C, Sohler W, Tittel W 2014 Phys. Rev. Lett. 113 053603
 Google Scholar
Google Scholar
[40] Harris S E, Field J E, Imamoğlu A 1990 Phys. Rev. Lett. 64 1107
 Google Scholar
Google Scholar
[41] Hau L V, Harris S E, Dutton Z, Behroozi C H 1999 Nature 397 594
 Google Scholar
Google Scholar
[42] Chanelière T, Matsukevich D N, Jenkins S D, Lan S Y, Kennedy T A B, Kuzmich A 2005 Nature 438 833
 Google Scholar
Google Scholar
[43] Nunn J, Walmsley I A, Raymer M G, Surmacz K, Waldermann F C, Wang Z, Jaksch D 2007 Phys. Rev. A 75 011401(R)
 Google Scholar
Google Scholar
[44] Reim K F, Nunn J, Lorenz V O, Sussman B J, Lee K C, Langford N K, Jaksch D, Walmsley I A 2010 Nat. Photon. 4 218
 Google Scholar
Google Scholar
[45] Reim K F, Michelberger P, Lee K C, Nunn J, Langford N K, Walmsley I A 2011 Phys. Rev. Lett. 107 053603
 Google Scholar
Google Scholar
[46] Moiseev S A, Kröll S 2001 Phys. Rev. Lett. 87 173601
 Google Scholar
Google Scholar
[47] Kraus B, Tittel W, Gisin N, Nilsson M, Kröll S, Cirac J I 2006 Phys. Rev. A 73 020302(R)
 Google Scholar
Google Scholar
[48] Afzelius M, Simon C, de Riedmatten H, Gisin N 2009 Phys. Rev. A 79 052329
 Google Scholar
Google Scholar
[49] Alexander A L, Longdell J J, Sellars M J, Manson N B 2006 Phys. Rev. Lett. 96 043602
 Google Scholar
Google Scholar
[50] Tittel W, Afzelius M, Chaneliére T, Cone R L, Kröll S, Moiseev S A, Sellars M 2010 Laser Photon. Rev. 4 244
 Google Scholar
Google Scholar
[51] Michelberger P S, Champion T F M, Sprague M R, Kaczmarek K T, Barbieri M, Jin X M, England D G, Kolthammer W S, Saunders D J, Nunn J, Walmsley I A 2015 New. J. Phys. 17 043006
 Google Scholar
Google Scholar
[52] Bustard P J, Lausten R, England D G, Sussman B J 2013 Phys. Rev. Lett. 111 083901
 Google Scholar
Google Scholar
[53] England D G, Bustard P J, Nunn J, Lausten R, Sussman B J 2013 Phys. Rev. Lett. 111 243601
 Google Scholar
Google Scholar
[54] Saunders D J, Munns J H D, Champion T F M, Qiu C, Kaczmarek K T, Poem E, Ledingham P M, Walmsley I A, Nunn J 2016 Phys. Rev. Lett. 116 090501
 Google Scholar
Google Scholar
[55] Kaczmarek K T, Ledingham P M, Brecht B, Thomas S E, Thekkadath G S, Lazo-Arjona O, Munns J H D, Poem E, Feizpour A, Saunders D J, Nunn J, Walmsley I A 2018 Phys. Rev. A 97 042316
 Google Scholar
Google Scholar
[56] Dou J P, Yang A L, Du M Y, Lao D, Gao J, Qiao L F, Li H, Pang X L, Feng Z, Tang H, Jin X M 2018 Commun. Phys. 1 55
 Google Scholar
Google Scholar
[57] Guo J X, Feng X T, Yang P Y, Yu Z F, Chen L Q, Yuan C H, Zhang W P 2018 arXiv: 1804.10763[quant-ph]
[58] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nat. Photon. 9 332
 Google Scholar
Google Scholar
[59] Zhang W, Ding D S, Dong M X, Shi S, Wang K, Liu S L, Li Y, Zhou Z Y, Shi B S, Guo G C 2016 Nat. Commun. 7 13514
 Google Scholar
Google Scholar
[60] Liu Y, Wu J H, Shi B S, Guo G C 2012 Chin. Phys. Lett. 29 024205
 Google Scholar
Google Scholar
[61] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
 Google Scholar
Google Scholar
[62] Franke-Arnold S, Allen L, Padgett M 2008 Laser Photon. Rev. 2 299
 Google Scholar
Google Scholar
[63] Leach J, Jack B, Romero J, Jha A K, Yao A M, Franke-Arnold S, Ireland D G, Boyd R W, Barnett S M, Padgett1 M J 2010 Science 329 662
 Google Scholar
Google Scholar
[64] Dada A C, Leach J, Buller G S, Padgett M J, Andersson E 2011 Nat. Phys. 7 677
 Google Scholar
Google Scholar
[65] Fickler R, Lapkiewicz R, Plick W M, Krenn M, Schaeff C, Ramelow S, Zeilinger A 2012 Science 338 640
 Google Scholar
Google Scholar
[66] Wang J, Yang J Y, Fazal I M, Ahmed N, Yan Y, Huang H, Ren Y X, Yue Y, Dolinar S, Tur M, Willner A E 2012 Nat. Photon. 6 488
 Google Scholar
Google Scholar
[67] Inoue R, Kanai N, Yonehara T, Miyamoto Y, Koashi M, Kozuma M 2006 Phys. Rev. A 74 053809
 Google Scholar
Google Scholar
[68] Inoue R, Yonehara T, Miyamoto Y, Koashi M, Kozuma M 2009 Phys. Rev. Lett. 103 110503
 Google Scholar
Google Scholar
[69] James D F V, Kwiat P G, Munro W J, White A G 2001 Phys. Rev. A 64 052312
 Google Scholar
Google Scholar
[70] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
 Google Scholar
Google Scholar
[71] Spengler C, Huber M, Brierley S, Adaktylos T, Hiesmayr B C 2012 Phys. Rev. A 86 022311
 Google Scholar
Google Scholar
[72] Hiesmayr B C, Löffler W 2013 New J. Phys. 15 083036
 Google Scholar
Google Scholar
[73] Collins D, Gisin N, Linden N, Massar S, Popescu S 2002 Phys. Rev. Lett. 88 040404
 Google Scholar
Google Scholar
[74] Romero J, Leach J, Jack B, Barnett S M, Padgett M J, Franke-Arnold S 2010 New J. Phys. 12 123007
 Google Scholar
Google Scholar
[75] Gühne O, Tóth G 2009 Phys. Rep. 474 1
 Google Scholar
Google Scholar
[76] Fickler R, Krenn M, Lapkiewicz R, Ramelow S, Zeilinger A 2013 Sci. Rep. 3 1914
 Google Scholar
Google Scholar
[77] Bruß D 2002 J. Math. Phys. 43 4237
 Google Scholar
Google Scholar
[78] Gühne O, Hyllus P, Bruß D, Ekert A, Lewenstein M, Macchiavello V, Sanpera A 2002 Phys. Rev. A 66 062305
 Google Scholar
Google Scholar
[79] Agnew M, Salvail J Z, Leach J, Boyd R E 2013 Phys. Rev. Lett. 111 030402
 Google Scholar
Google Scholar
[80] Krenn M, Huber M, Fickler R, Lapkiewicz R, Ramelow S, Zeilinger A 2014 Proc. Natl. Acad. Sci. U.S.A. 111 6243
 Google Scholar
Google Scholar
[81] Choi K S, Deng H, Laurat J, Kimble H J 2008 Nature 452 67
 Google Scholar
Google Scholar
[82] Kwiat P G 1997 J. Mod. Opt. 44 2173
 Google Scholar
Google Scholar
[83] Barreiro J T, Langford N K, Peters N A, Kwiat P G 2005 Phys. Rev. Lett. 95 260501
 Google Scholar
Google Scholar
[84] Schuck C, Huber G, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 190501
 Google Scholar
Google Scholar
[85] Bozinovic1 N, Yue Y, Ren Y X, Tur M, Kristensen P, Huang H, Willner A E, Ramachandran S 2013 Science 340 1545
 Google Scholar
Google Scholar
[86] Walborn W S, Pádua S, Monken C H 2003 Phys. Rev. A 68 042313
 Google Scholar
Google Scholar
[87] Calsamiglia J, Lütkenhaus N 2001 Appl. Phys. B 72 67
 Google Scholar
Google Scholar
[88] Barreiro J T, Wei T C, Kwiat P G 2008 Nat. Phys. 4 282
 Google Scholar
Google Scholar
[89] Tiranov A, Lavoie J, Ferrier A, Goldner P, Verma V B, Nam S W, Mirin R P, Lita A E, Marsili F, Herrmann H, Silberhorn C, Gisin N, Afzelius M, Bussières F 2015 Optica 2 279
 Google Scholar
Google Scholar
-
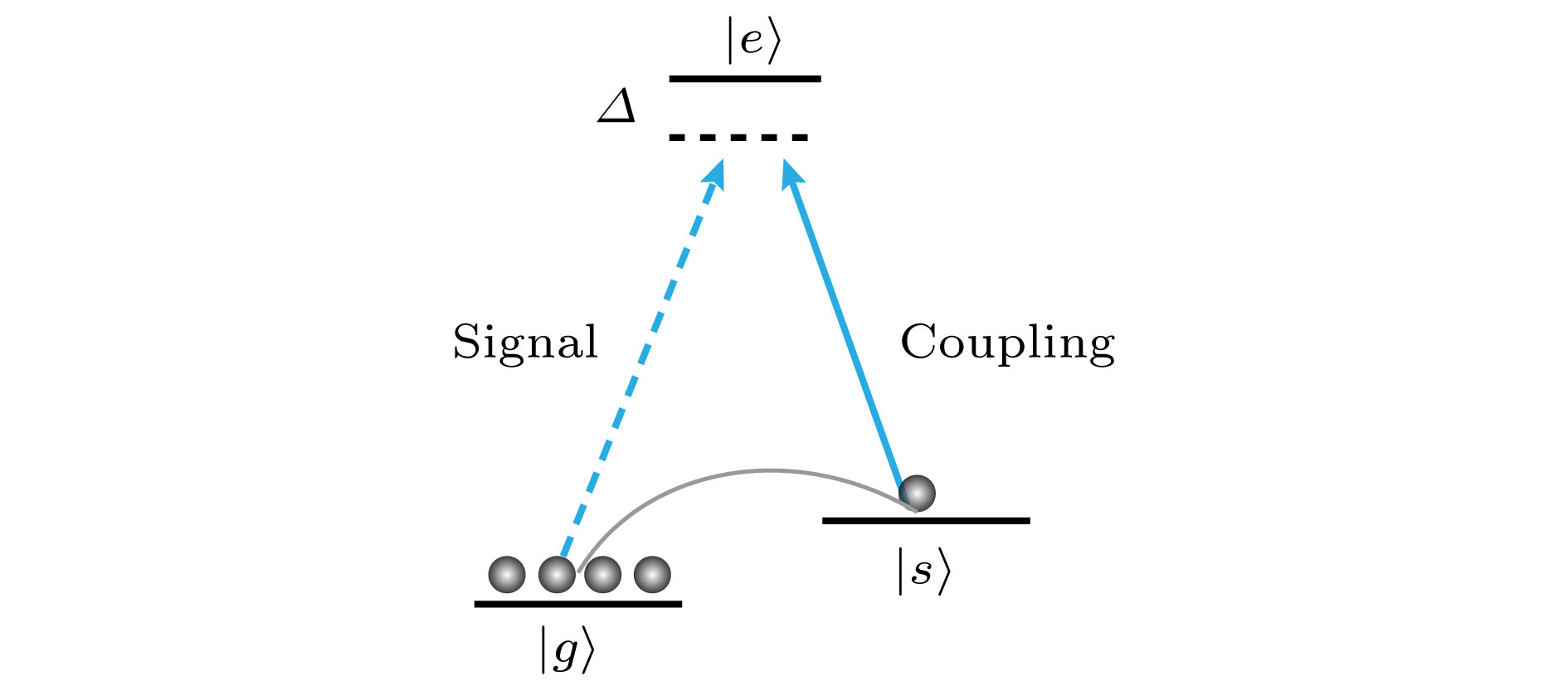
图 1 拉曼存储方案能级简图, 其中
$\left| g \right\rangle $ ,$\left| s \right\rangle $ 和$\left| e \right\rangle $ 分别表示基态、亚稳态和激发态;$\varDelta $ 表示失谐量Figure 1. Simplified energy level diagram for Raman protocol.
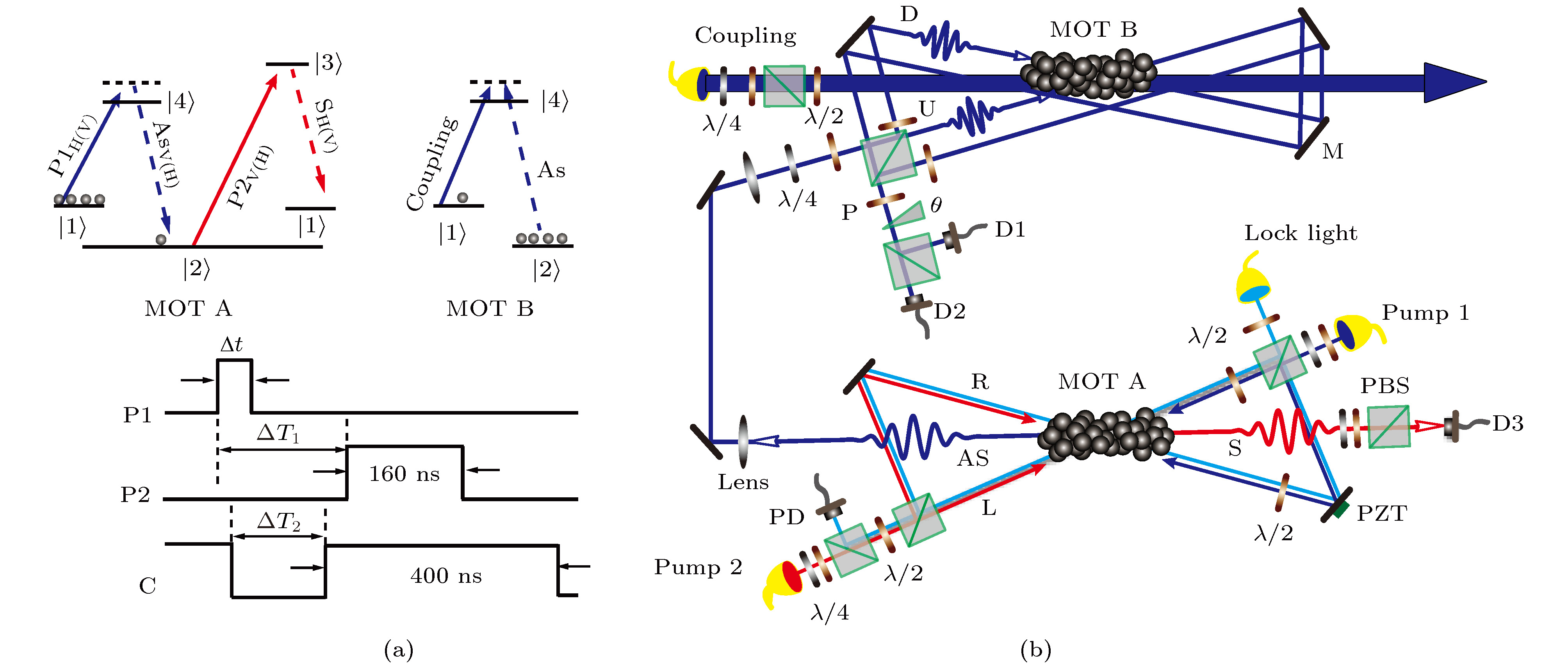
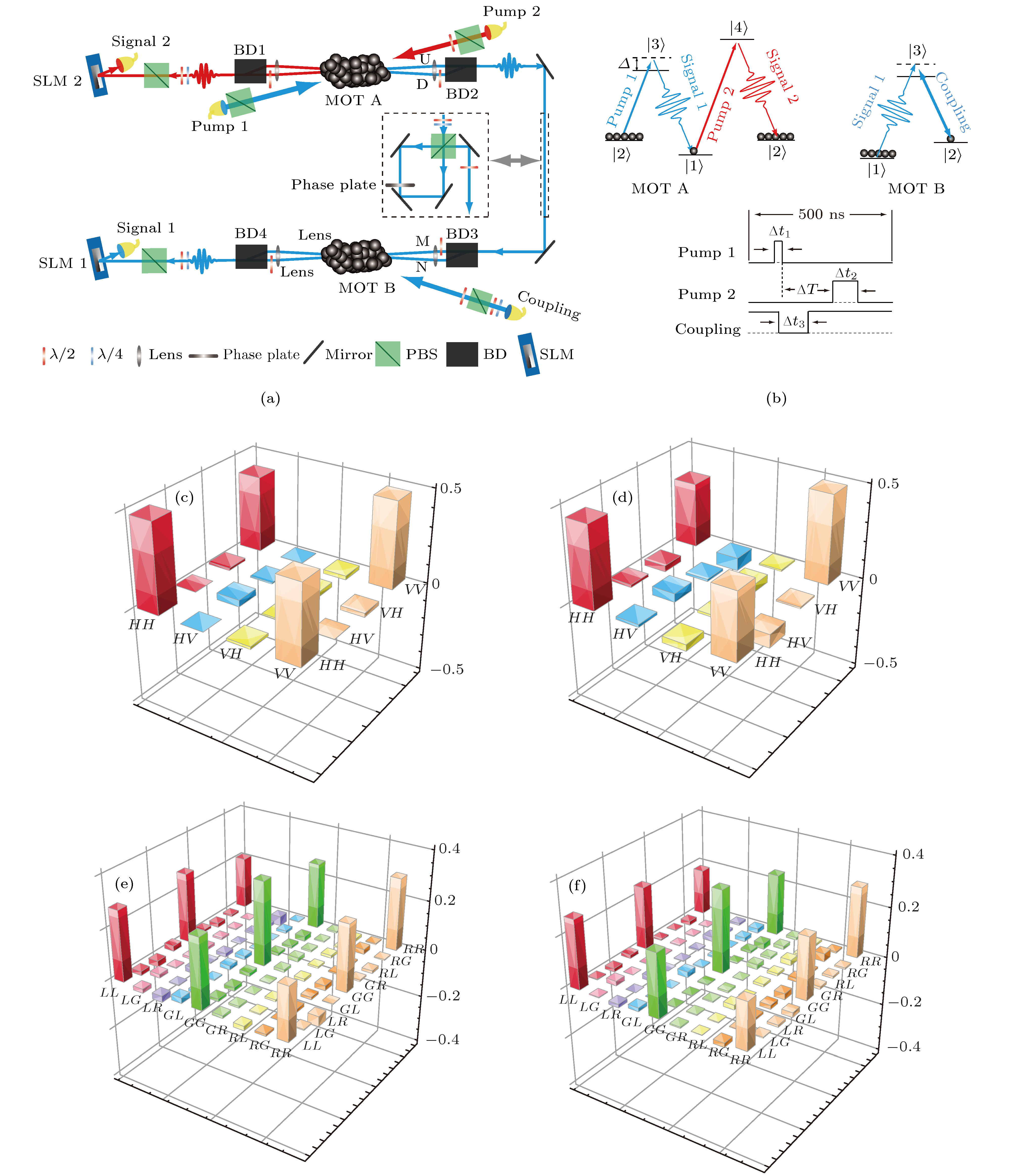
$\left| g \right\rangle $ ,$\left|s\right\rangle $ and$\left| e \right\rangle $ correspond to ground, metastable and excited state respectively;$\varDelta $ represents detuning.图 2 简化的能级图和实验装置图[29] (a)简化的SRS能级图, 态
$\left| 1 \right\rangle $ 和$\left| 2 \right\rangle $ 分别对应于85Rb原子的两个亚稳态能级5S1/2 (F = 3)和5S1/2(F = 2),$\left| 3 \right\rangle $ 和$\left| 4 \right\rangle $ 分别对应激发态能级5P3/2(F' = 3)和5P1/2(F' = 3); 泵浦光1由外腔二极管激光器(DL100, Toptica) 产生, 波长为795 nm, 与原子跃迁5S1/2(F = 3)→5P1/2(F' = 3)蓝失谐值70 MHz; 泵浦光2来自另一个波长为780 nm的外腔二极管激光器(DL100, Toptica), 对应5S1/2(F = 2)→5P3/2(F' = 3)的原子跃迁; 泵浦光1和泵浦光2被调制成脉冲模式, 脉冲宽度分别为50和160 ns, 上升沿为30 ns; 在存储过程中泵浦1和泵浦2脉冲之间的延迟时间被设置为260 ns; 泵浦1和泵浦2的激光功率分别为0.5和4 mW; 控制光来自于与泵浦光1相同的激光器, 也对应于原子跃迁5S1/2(F = 3)到5P1/2(F' = 3), 并蓝失谐值70 MHz, 功率为12 mW; (b)实验装置简化图, MOT 2中信号1的束腰为63${\text{μm}}$ (MOT, 磁光阱; FC, 光纤耦合器; SLM, 空间光调制器; PBS, 偏振分束器;$\lambda$ /2, 半波片)Figure 2. Simplified energy level diagram and experimental setup[29]. (a) Simplified energy level diagram of the SRS. The states
$\left| 1 \right\rangle $ and$\left| 2 \right\rangle $ correspond to two metastable levels 5S1/2(F = 3) and 5S1/2(F = 2) of 85Rb atom respectively,$\left| 3 \right\rangle $ and$\left| 4 \right\rangle $ are the excited levels of 5P3/2(F' = 3) and 5P1/2(F' = 3) respectively. The pump 1 laser is from an external-cavity diode laser (DL100, Toptica) with the wavelength of 795 nm, and is blue-detuned to the atomic transition of 5S1/2(F = 3)→5P1/2(F' = 3) with a value of 70 MHz. The pump 2 laser is from another external-cavity diode laser (DL100, Toptica) with the wavelength of 780 nm which couples the atomic transition of 5S1/2(F = 2)→5P3/2(F' = 3). The pump 1 and pump 2 are modulated into pulse modes with a width of 50 and 160 ns respectively, and a rising edge of 30 ns. The delayed time between the pump 1 pulse and the pump 2 pulse is programmed to be 260 ns for the process of storage. The powers of pump 1 and pump 2 are 0.5 and 4 mW respectively. The coupling laser is from the same laser with pump 1 and is also blue-detuned to atomic transition of 5S1/2(F = 3)→5P1/2(F' = 3) with a value of 70 MHz, its power is about 12 mW. (b) Simplified diagram depicting the storage of entanglement of OAM state. The waist of signal 1 at MOT 2 was 63${\text{μm}}$ . MOT, magneto-optical trap; FC, fibre coupler; SLM, spatial light modulator; PBS, polarisation beam splitter;$\lambda$ /2, half-wave plate.图 3 存储过程中的交叉相关函数
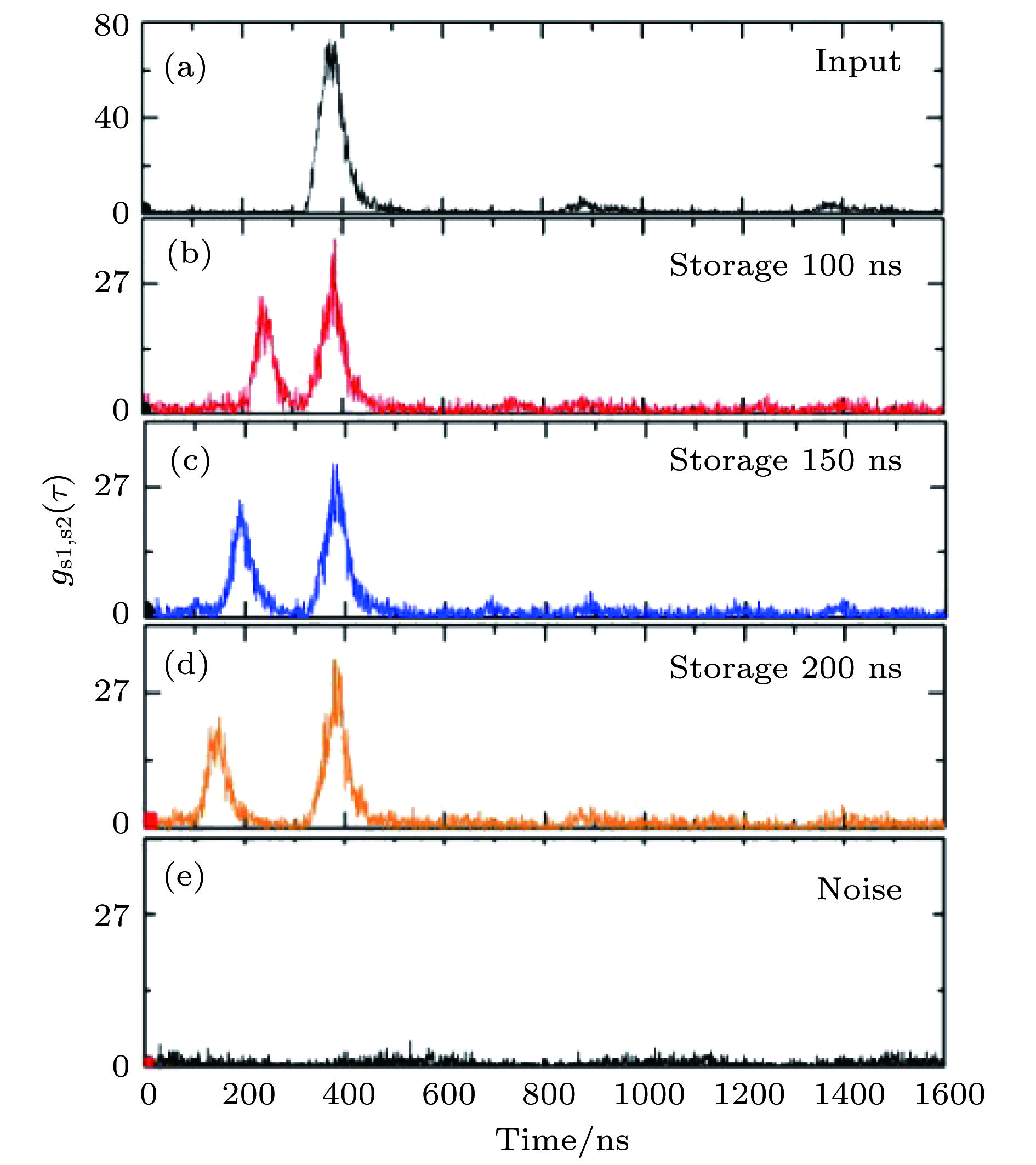
${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right)$ [58] (a)信号光子1和信号光子2之间的交叉相关函数${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right)$ , 泵浦1和泵浦2之间延迟时间为260 ns; (b), (c)和(d)是信号光子2与读出的信号光子1之间的时间相关函数${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right),$ 信号光子1的存储时间分别为100, 150和200 ns; (e)在没有输入信号1至MOT2的情况下收集的噪音; 所有数据均为原始数据, 无噪声校正Figure 3. Cross-correlated function of
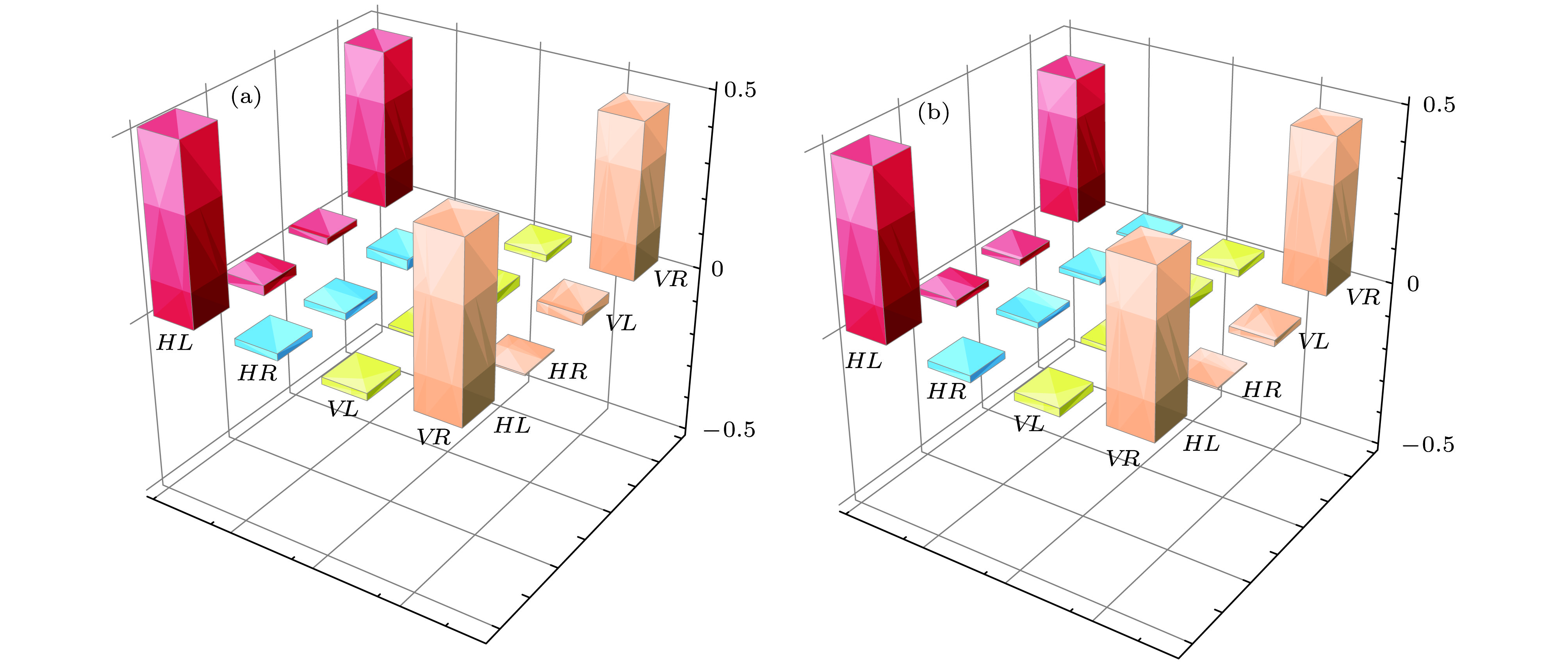
${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right)$ in the process of storage[58]: (a) Cross-correlated function${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right)$ between signal 1 and signal 2 photons with a delayed time of 260 ns between pump 1 and pump 2; (b), (c) and (d) were the time-correlated function${g_{{\rm{s}}1,{\rm{s}}2}}\left( \tau \right)$ between signal 2 photon and the retrieval signal 1 photon with storage time of 100, 150 and 200 ns respectively; (e) the collected noise without the input signal. The signal 1 acted as trigger photon, and the signal 2 acted as stop signal. All data were raw, without noise correction.图 6 存储前后重构的密度矩阵[29] (a)用于重构密度矩阵的OAM态; (b)/(d)和(c)/(e)分别是存储前/后重构密度矩阵的实部和虚部, 背景噪声已被减去; 其中(b)和(c)中每组测量时间为500 s, (d)和(e)中每组测量时间为1000 s; L/R分别表示OAM为1/−1.
Figure 6. Reconstructed density matrices before and after storage[29]: (a) Four OAM states for reconstructing density matrix; (b)/(d) and (c)/(e) are the real and imaginary parts of the reconstructed density matrix of the state before/after storage respectively. The background noise has been subtracted. The background noise was estimated by repeating the experiment without input signal 1 photon to MOT 2. The measurement time for each data was 500 s in (b) and (c) and 1000 s in (d) and (e). L/R represents OAM = 1/−1.
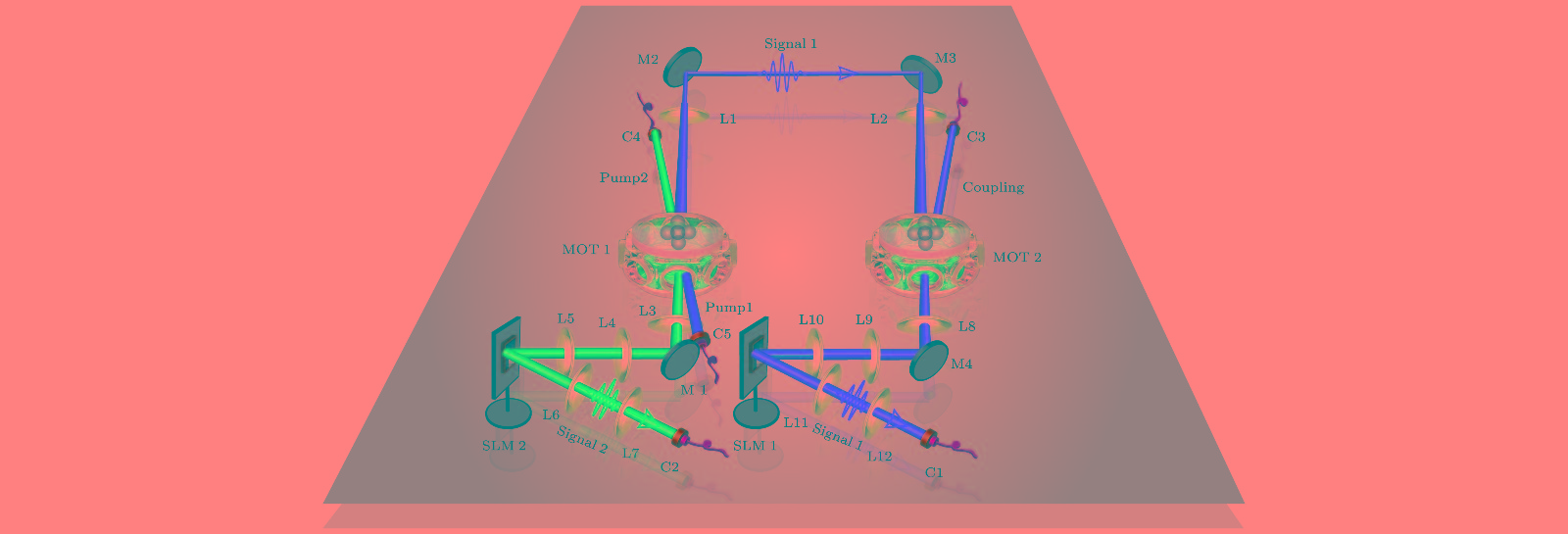
图 7 实验装置[30], 其中透镜L1和L2用于将信号1的相位结构映射到MOT2的中心; 利用L3, L4和L5将位于MOT1中心的信号2的相位结构映射到SLM2的表面; L6和L7用于将信号2的OAM模式耦合到C2中; 图的右侧部分用于将信号1存储在MOT2, 并在读出后将其耦合到C1; C, 光纤耦合器; M, 反射镜; L, 透镜
Figure 7. Experimental setup[30]. Lenses L1 and L2 are used to focus signal 1 on the centre of MOT 2. L3, L4, and L5 are used to focus the phase structure of signal 2 on the center of MOT 1 onto the surface of SLM 2. L6 and L7 are used to couple OAM mode of signal 2 to C2. There is an asymmetric optical path for coupling signal 1 into C1 in right frame of figure. C, fiber coupler; M, mirror; L, lens.
图 10 (a) 简化的能级图, 用于产生和存储偏振纠缠和单光子的生成、存储的时序; P1是泵浦光1, P2是泵浦光2; (b)简化的实验装置; L和R是MOT A中的两个SRS过程, H和V分别代水平极化和垂直极化, P1和P2分别为来自两个声光调制器的25 ns (
$\Delta t $ )和160 ns的调制脉冲; MOT, 磁光阱; FC, 光纤耦合器; PBS, 偏振分束器;$\lambda$ /2, 半波片;$\lambda$ /4, 四分之一波片; S, Stokes光子; As, 反-Stokes光子; D1, D2和D3分别是单光子探测器1, 2和3 (PerkinElmer SPCM-AQR-15-FC); PD, 自制光电探测器; PZT, 压电陶瓷; U和D分别是输入到MOT B中的上和下光模式; P, 半波板;$\theta$ , 插入相位板的相位[58]Figure 10. (a) Simplified energy level diagram used to generate and store the polarization entanglement and the time sequence for the generation, storage and retrieval sequence of a single photon. P1 is pump 1 and P2 is pump 2. (b) Ssimplified setup depicting the storage of the polarization entanglement. L and R are the two SRS processes in MOT A. H and V are the horizontal and vertical polarizations, respectively. P1 and P2 are the modulated pulses with 25 ns (
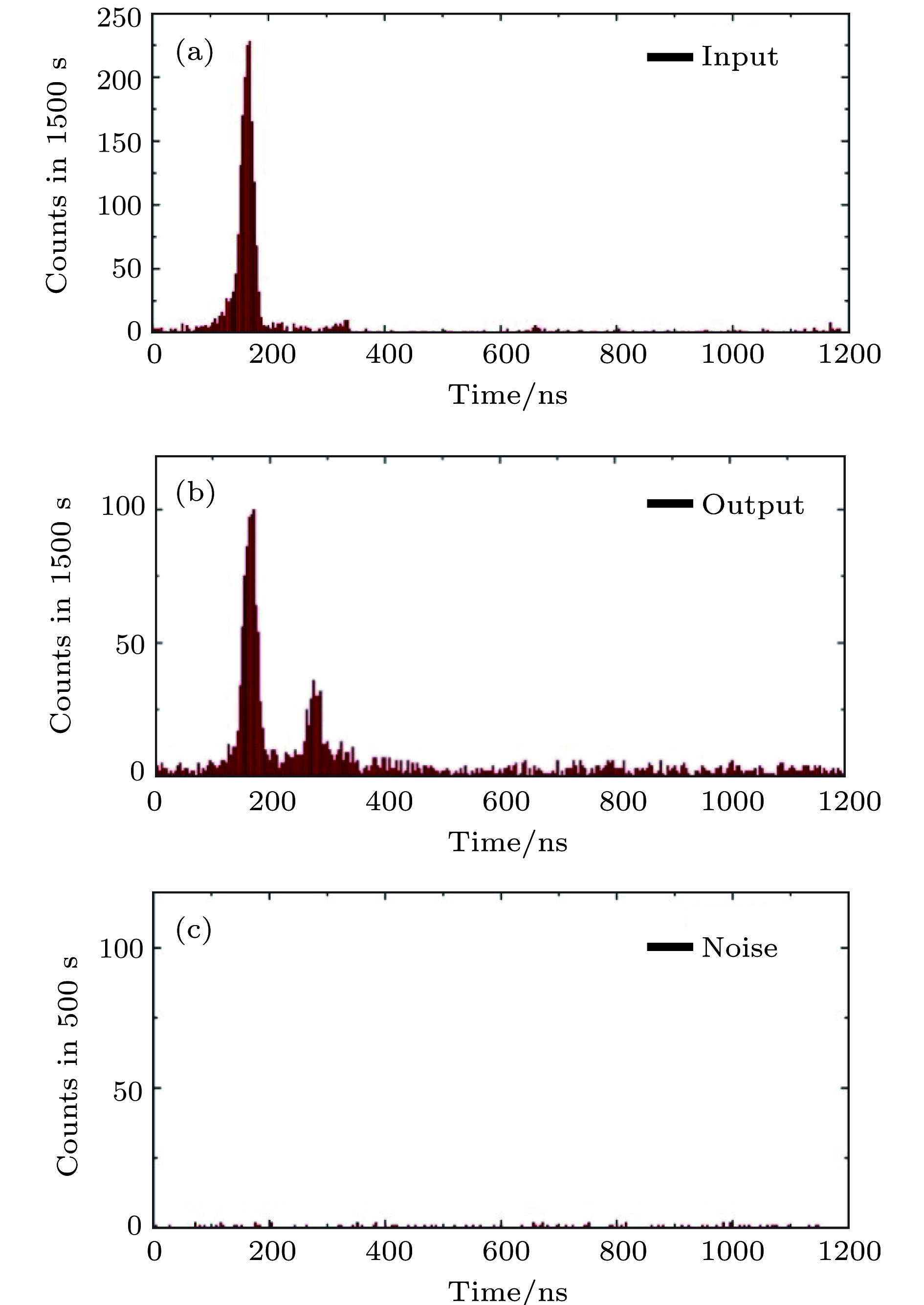
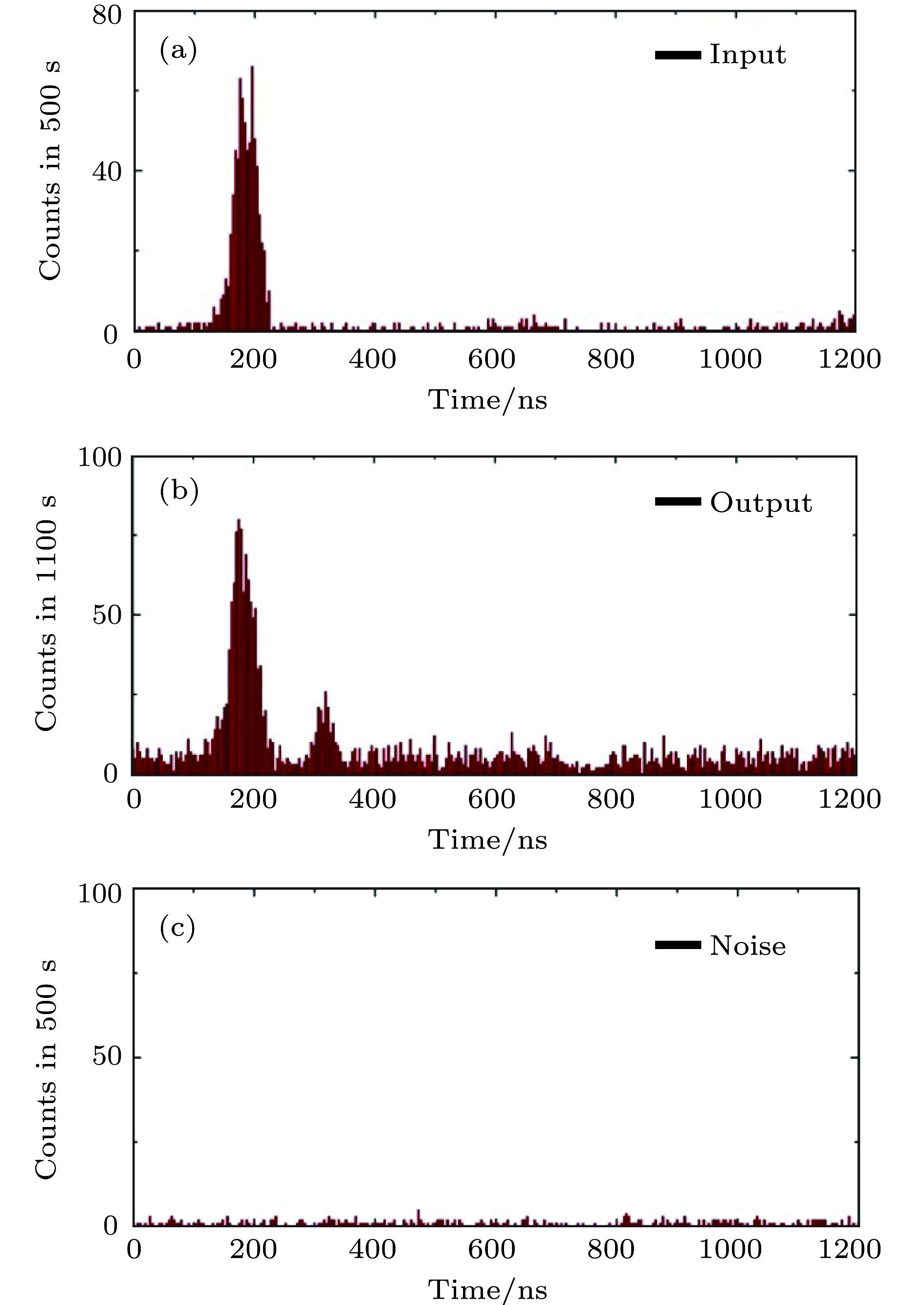
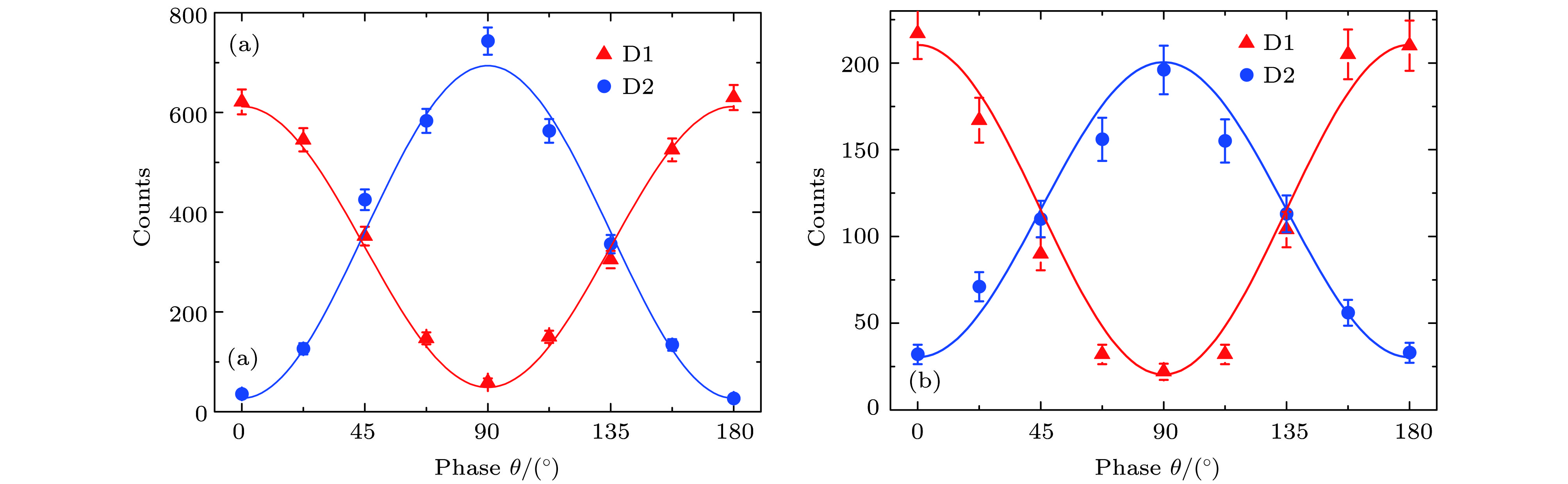
$\Delta t $ ) and 160 ns from two acoustic optic modulators, respectively. MOT, magneto-optical trap; FC, fibre coupler; PBS, polarization beam splitter;$\lambda$ /2, half-wave plate;$\lambda$ /4, quarter-wave plate; S, Stokes photon; As, anti-Stokes photon; D1, D2 and D3 are single photon detectors 1, 2 and 3, respectively (PerkinElmer SPCM-AQR-15-FC); PD, home-made photoelectric detector; PZT, piezoelectric transducer; U and D are the up- and down-optical modes input into MOT B, respectively; P, half-wave plate;$\theta$ , the phase of the inserted phase plate [58].图 11 (a) 和(b) 分别为存储前后探测器D3探测到的Stokes光子与探测器D1 (圆形数据)和探测器D2 (三角形数据)分别探测到的反Stokes光子之间的符合计数; 实线是拟合曲线; 所有实验数据为原始数据, 没有进行误差校正; 误差为 ± 1的标准差[58]
Figure 11. (a) and (b) Coincidence between the Stokes photon detected by detector D3 and the anti-Stokes photon detected by detector D1 (circular data) and detector D2 (triangular data), respectively, with a different phase before/after storage. The solid lines are the fitted lines. All of the experimental data are raw data without error corrections. The error bars are ± 1 standard deviation [58].
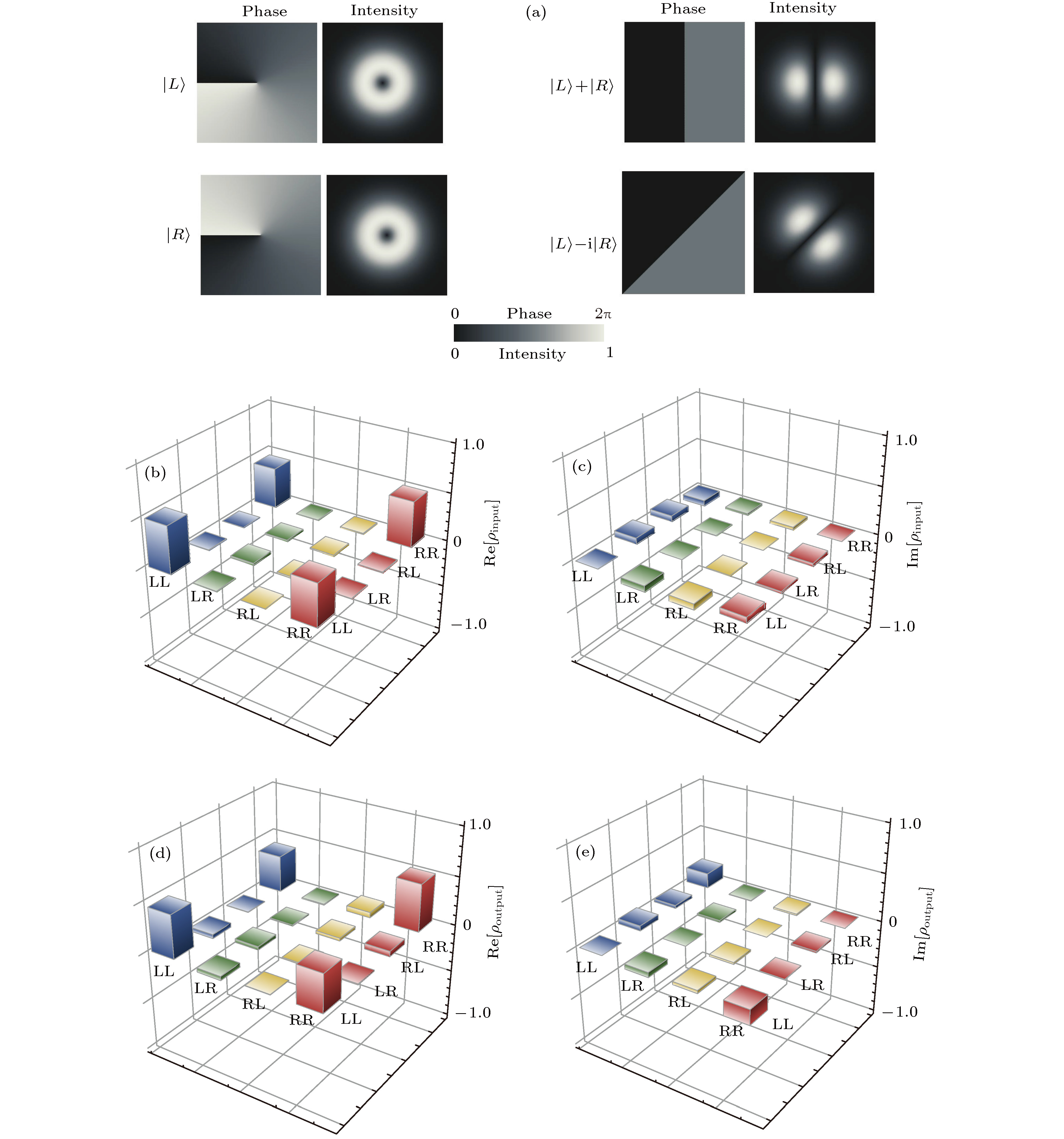
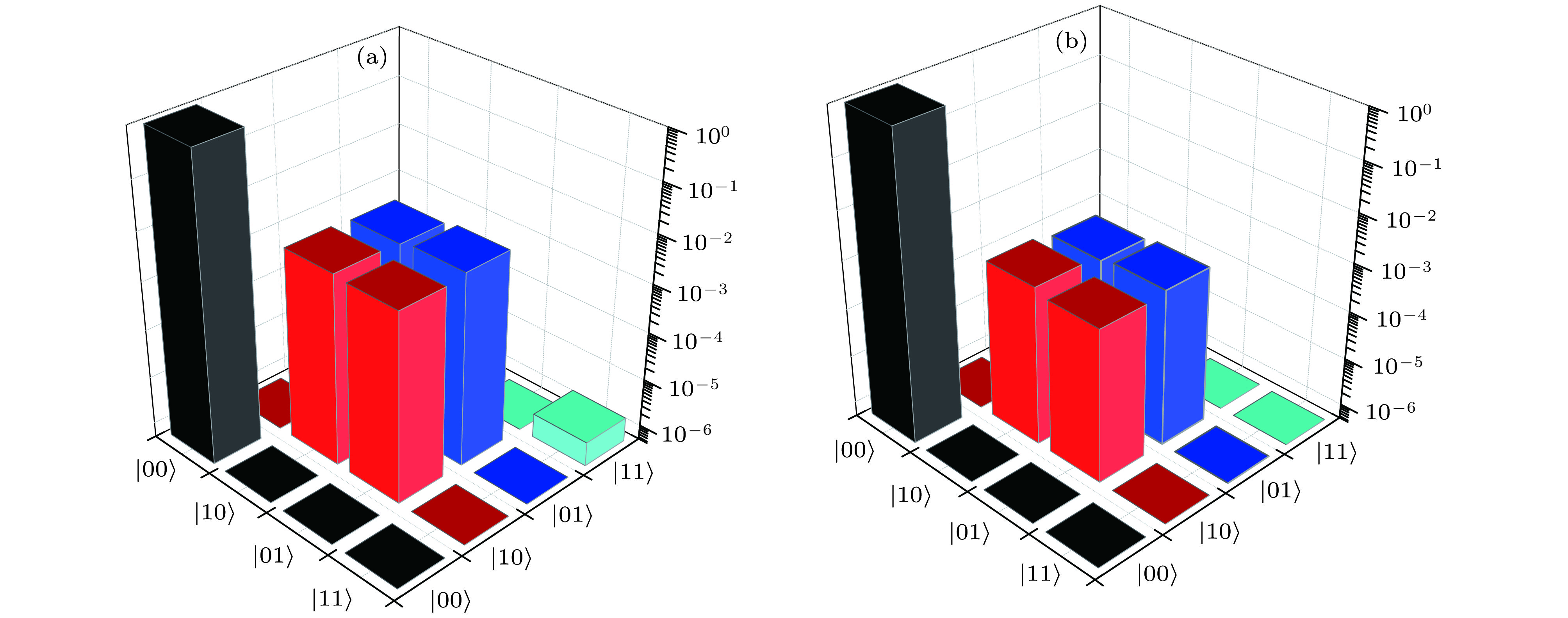
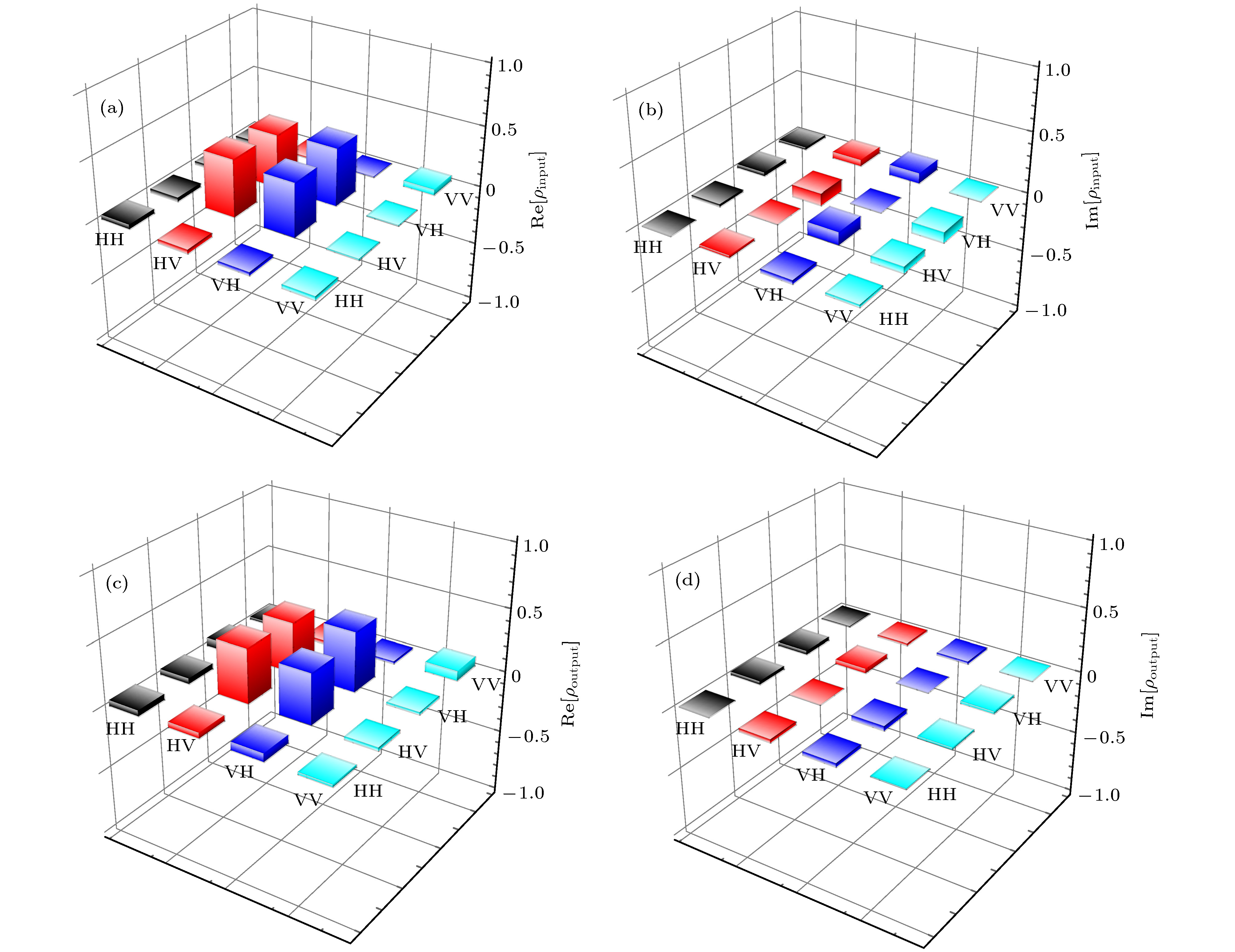
图 13 (a)/(c)和(b)/(d)分别为输入/输出的重构密度矩阵的实部和虚部; 所有实验数据为原始数据, 无误差校正[58]
Figure 13. (a)/(c) and (b)/(d) Reconstructed real and imaginary parts of the input/output density matrix, respectively. The density matrices were reconstructed with losses. All of the experimental data are raw data without error corrections[58].
图 14 多个DOF超纠缠的产生和存储[59] (a)实验装置简化图; (b)能级图和时间序列; 二维极化纠缠((c), (d))和三维OAM纠缠((e), (f))的构造密度矩阵的实部, 其中(c), (e)对应存储前; (d), (f))对应于存储后.
Figure 14. Generation and storage of entanglement in multiple DOFs [59]: (a) Simplified experimental set-up; (b) energy diagram and time sequence; the real parts of the constructed density matrices for the two-dimensional polarization entanglement ((c), (d)) and the three-dimensional OAM entanglement ((e), (f)), before ((c), (e)) and after ((d), (f)) storage.
图 16 杂化纠缠的双光子关联干涉曲线[59] (a)存储前; (b)存储后; 误差由泊松统计估计, 表示为 ± s.d; 所有数据均为原始数据, 没有进行误差纠正
Figure 16. Interference curves of the two-photon correlations for hybrid entanglement [59]: (a) Before storage; (b) after storage. The error bars are estimated from Poisson statistics and represent as ± s.d. All the data are raw and not subjected to noise correction.
表 1 存储前后的
${\bar p_{ij}}$ 以及$\bar C$ Table 1. Values of
${\bar p_{ij}}$ and$\bar C$ before and after storage.${\bar \rho _{{\rm{input}}}}$ ${\bar \rho _{{\rm{output}}}}$ ${\bar p_{00}}$ 0.990393 ± 0.00006 0.998166 ± 0.000008 ${\bar p_{10}}$ (4.59 ± 0.03) × 10−3 (9.64 ± 0.04) × 10−4 ${\bar p_{01}}$ (5.04 ± 0.03) × 10−3 (8.71 ± 0.04) × 10−4 ${\bar p_{11}}$ (1.6 ± 0.2) × 10−6 (5 ± 5) × 10−8 $\bar C$ (5.8 ± 0.2) × 10−3 (1.2 ± 0.4) × 10−3 -
[1] Sangouard N, Simon C, Zhao B, Chen Y A, de Riedmatten H, Pan J W, Gisin N 2008 Phys. Rev. A 77 062301
 Google Scholar
Google Scholar
[2] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
 Google Scholar
Google Scholar
[3] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
 Google Scholar
Google Scholar
[4] Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O'Brien J L 2010 Nature 464 54
 Google Scholar
Google Scholar
[5] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photon. 5 222
 Google Scholar
Google Scholar
[6] Majumdar A, Bajcsy M, Rundquist A, Vučković J 2012 Phys. Rev. Lett. 108 183601
 Google Scholar
Google Scholar
[7] Bussières F, Sangouard N, Afzelius M, de Riedmatten H, Simon C, Tittel W 2013 J. Mod. Opt. 60 1519
 Google Scholar
Google Scholar
[8] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
 Google Scholar
Google Scholar
[9] Radnaev A G, Dudin Y O, Zhao R, Jen H H, Jenkins S D, Kuzmich A, Kennedy T A B 2010 Nat. Phys. 6 894
 Google Scholar
Google Scholar
[10] Albrecht B, Farrera P, Gonzalvo X F, Cristiani M, de Riedmatten H 2014 Nat. Commun. 5 3376
 Google Scholar
Google Scholar
[11] Clausen C, Usmani I, Bussières F, Sangouard N, Afzelius M, de Riedmatten H, Gisin N 2011 Nature 469 508
 Google Scholar
Google Scholar
[12] Saglamyurek E, Sinclair N, Jin J, Slater J A, Oblak D, Bussières F, George M, Ricken R, Sohler W, Tittel W 2011 Nature 469 512
 Google Scholar
Google Scholar
[13] Simon C, de Riedmatten H, Afzelius M, Sangouard N, Zbinden H, Gisin N 2007 Phys. Rev. Lett. 98 190503
 Google Scholar
Google Scholar
[14] Zhang W, Ding D S, Shi S, Li Y, Zhou Z Y, Shi B S, Guo G C 2016 Phys. Rev. A 93 022316
 Google Scholar
Google Scholar
[15] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
 Google Scholar
Google Scholar
[16] Olmschenk S, Matsukevich D N, Maunz P, Hayes D, Duan L M, Monroe C 2009 Science 323 486
 Google Scholar
Google Scholar
[17] Kurz C, Schug M, Eich P, Huwer J, Müller P, Eschner J 2014 Nat. Commun. 5 5527
 Google Scholar
Google Scholar
[18] Togan E, Chu Y, Trifonov A S, Jiang L, Maze J, Childress L, Dutt M V G, Sørensen A S, Hemmer P R, Zibrov A S, Lukin M D 2010 Nature 466 730
 Google Scholar
Google Scholar
[19] Bernien H, Hensen B, Pfaff W, Koolstra G, Blok M S, Robledo L, Taminiau T H, Markham M, Twitchen D J, Childress L, Hanson R 2013 Nature 497 86
 Google Scholar
Google Scholar
[20] Greve D G, Yu L, McMahon P L, Pelc J S, Natarajan C M, Kim N Y, Abe E, Maier S, Schneider C, Kamp M, Höfling S, Hadfield R H, Forchel A, Fejer M M, Yamamoto Y 2012 Nature 491 421
 Google Scholar
Google Scholar
[21] Wang Q, Zhang Y S 2012 Eur. Phys. J. B 85 225
 Google Scholar
Google Scholar
[22] Dudin Y O, Li L, Kuzmich A 2013 Phys. Rev. A 87 031801
 Google Scholar
Google Scholar
[23] Xu Z X, Wu Y L, Tian L, Chen L, Zhang Z Y, Yan Z H, Li S J, Wang H, Xie C D, Peng K C 2013 Phys. Rev. Lett. 111 240503
 Google Scholar
Google Scholar
[24] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y H, Chen Y F, Yu I A, Chen Y C 2018 Phys. Rev. Lett. 120 183602
 Google Scholar
Google Scholar
[25] Zhou S, Zhang S C, Liu C, Chen J F, Wen J M, Loy M M T, Wong G K L, Du S W 2012 Opt. Express. 20 24124
 Google Scholar
Google Scholar
[26] Li J F, Wang Y F, Zhang S C, He J Y, Cheng A Q, Yan H, Zhu S L 2017 arXiv: 1706.01404[quant-ph]
[27] Ding D S, Zhou Z Y, Shi B S, Guo G C 2013 Nat. Commun. 4 2527
 Google Scholar
Google Scholar
[28] Ding D S, Zhang W, Zhou Z Y, Shi S, Pan J S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2014 Phys. Rev. A 90 042301
 Google Scholar
Google Scholar
[29] Ding D S, Zhang W, Zhou Z Y, Shi S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2015 Phys. Rev. Lett. 114 050502
 Google Scholar
Google Scholar
[30] Ding D S, Zhang W, Shi S, Zhou Z Y, Li Y, Shi B S, Guo G C 2016 Light: Science and Applications 5 e 5 e16157
 Google Scholar
Google Scholar
[31] Shi B S, Ding D S, Zhang W 2018 J. Phys. B: At. Mol. Opt. Phys. 51 032004
 Google Scholar
Google Scholar
[32] Hosseini M, Sparkes B M, Campbell G, Lam P K, Buchler B C 2011 Nat. Commun. 2 174
 Google Scholar
Google Scholar
[33] Higginbottom D B, Sparkes B M, Rancic M, Pinel O, Hosseini M, Lam P K, Buchler B C 2012 Phys. Rev. A 86 023801
 Google Scholar
Google Scholar
[34] Glorieux Q, Clark J B, Marino A M, Zhou Z F, Lett P D 2012 Opt. Express 20 12350
 Google Scholar
Google Scholar
[35] Shi S, Ding D S, Zhang W, Zhou Z Y, Dong M X, Liu S L, Wang K, Shi B S, Guo G C 2017 Phys. Rev. A 95 033823
 Google Scholar
Google Scholar
[36] Ding D S, Wu J H, Zhou Z Y, Liu Y, Shi B S, Zou X B, Guo G C 2013 Phys. Rev. A 87 013835
 Google Scholar
Google Scholar
[37] Zhong M J, Hedges M P, Ahlefeldt R L, Bartholomew J G, Beavan S E, Wittig S M, Longdell J J, Sellars M J 2015 Nature 517 177
 Google Scholar
Google Scholar
[38] Tang, J S, Zhou Z Q, Wang Y T, Li Y L, Liu X, Hua Y L, Zou Y, Wang S, He D Y, Chen G, Sun Y N, Yu Y, Li M F, Zha Z G, Ni H Q, Niu Z C, Li C F, Guo G C 2015 Nat. Commun. 6 8652
 Google Scholar
Google Scholar
[39] Sinclair N, Saglamyurek E, Mallahzadeh H, Slater J A., George M, Ricken R, Hedges M P, Oblak D, Simon C, Sohler W, Tittel W 2014 Phys. Rev. Lett. 113 053603
 Google Scholar
Google Scholar
[40] Harris S E, Field J E, Imamoğlu A 1990 Phys. Rev. Lett. 64 1107
 Google Scholar
Google Scholar
[41] Hau L V, Harris S E, Dutton Z, Behroozi C H 1999 Nature 397 594
 Google Scholar
Google Scholar
[42] Chanelière T, Matsukevich D N, Jenkins S D, Lan S Y, Kennedy T A B, Kuzmich A 2005 Nature 438 833
 Google Scholar
Google Scholar
[43] Nunn J, Walmsley I A, Raymer M G, Surmacz K, Waldermann F C, Wang Z, Jaksch D 2007 Phys. Rev. A 75 011401(R)
 Google Scholar
Google Scholar
[44] Reim K F, Nunn J, Lorenz V O, Sussman B J, Lee K C, Langford N K, Jaksch D, Walmsley I A 2010 Nat. Photon. 4 218
 Google Scholar
Google Scholar
[45] Reim K F, Michelberger P, Lee K C, Nunn J, Langford N K, Walmsley I A 2011 Phys. Rev. Lett. 107 053603
 Google Scholar
Google Scholar
[46] Moiseev S A, Kröll S 2001 Phys. Rev. Lett. 87 173601
 Google Scholar
Google Scholar
[47] Kraus B, Tittel W, Gisin N, Nilsson M, Kröll S, Cirac J I 2006 Phys. Rev. A 73 020302(R)
 Google Scholar
Google Scholar
[48] Afzelius M, Simon C, de Riedmatten H, Gisin N 2009 Phys. Rev. A 79 052329
 Google Scholar
Google Scholar
[49] Alexander A L, Longdell J J, Sellars M J, Manson N B 2006 Phys. Rev. Lett. 96 043602
 Google Scholar
Google Scholar
[50] Tittel W, Afzelius M, Chaneliére T, Cone R L, Kröll S, Moiseev S A, Sellars M 2010 Laser Photon. Rev. 4 244
 Google Scholar
Google Scholar
[51] Michelberger P S, Champion T F M, Sprague M R, Kaczmarek K T, Barbieri M, Jin X M, England D G, Kolthammer W S, Saunders D J, Nunn J, Walmsley I A 2015 New. J. Phys. 17 043006
 Google Scholar
Google Scholar
[52] Bustard P J, Lausten R, England D G, Sussman B J 2013 Phys. Rev. Lett. 111 083901
 Google Scholar
Google Scholar
[53] England D G, Bustard P J, Nunn J, Lausten R, Sussman B J 2013 Phys. Rev. Lett. 111 243601
 Google Scholar
Google Scholar
[54] Saunders D J, Munns J H D, Champion T F M, Qiu C, Kaczmarek K T, Poem E, Ledingham P M, Walmsley I A, Nunn J 2016 Phys. Rev. Lett. 116 090501
 Google Scholar
Google Scholar
[55] Kaczmarek K T, Ledingham P M, Brecht B, Thomas S E, Thekkadath G S, Lazo-Arjona O, Munns J H D, Poem E, Feizpour A, Saunders D J, Nunn J, Walmsley I A 2018 Phys. Rev. A 97 042316
 Google Scholar
Google Scholar
[56] Dou J P, Yang A L, Du M Y, Lao D, Gao J, Qiao L F, Li H, Pang X L, Feng Z, Tang H, Jin X M 2018 Commun. Phys. 1 55
 Google Scholar
Google Scholar
[57] Guo J X, Feng X T, Yang P Y, Yu Z F, Chen L Q, Yuan C H, Zhang W P 2018 arXiv: 1804.10763[quant-ph]
[58] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nat. Photon. 9 332
 Google Scholar
Google Scholar
[59] Zhang W, Ding D S, Dong M X, Shi S, Wang K, Liu S L, Li Y, Zhou Z Y, Shi B S, Guo G C 2016 Nat. Commun. 7 13514
 Google Scholar
Google Scholar
[60] Liu Y, Wu J H, Shi B S, Guo G C 2012 Chin. Phys. Lett. 29 024205
 Google Scholar
Google Scholar
[61] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
 Google Scholar
Google Scholar
[62] Franke-Arnold S, Allen L, Padgett M 2008 Laser Photon. Rev. 2 299
 Google Scholar
Google Scholar
[63] Leach J, Jack B, Romero J, Jha A K, Yao A M, Franke-Arnold S, Ireland D G, Boyd R W, Barnett S M, Padgett1 M J 2010 Science 329 662
 Google Scholar
Google Scholar
[64] Dada A C, Leach J, Buller G S, Padgett M J, Andersson E 2011 Nat. Phys. 7 677
 Google Scholar
Google Scholar
[65] Fickler R, Lapkiewicz R, Plick W M, Krenn M, Schaeff C, Ramelow S, Zeilinger A 2012 Science 338 640
 Google Scholar
Google Scholar
[66] Wang J, Yang J Y, Fazal I M, Ahmed N, Yan Y, Huang H, Ren Y X, Yue Y, Dolinar S, Tur M, Willner A E 2012 Nat. Photon. 6 488
 Google Scholar
Google Scholar
[67] Inoue R, Kanai N, Yonehara T, Miyamoto Y, Koashi M, Kozuma M 2006 Phys. Rev. A 74 053809
 Google Scholar
Google Scholar
[68] Inoue R, Yonehara T, Miyamoto Y, Koashi M, Kozuma M 2009 Phys. Rev. Lett. 103 110503
 Google Scholar
Google Scholar
[69] James D F V, Kwiat P G, Munro W J, White A G 2001 Phys. Rev. A 64 052312
 Google Scholar
Google Scholar
[70] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880
 Google Scholar
Google Scholar
[71] Spengler C, Huber M, Brierley S, Adaktylos T, Hiesmayr B C 2012 Phys. Rev. A 86 022311
 Google Scholar
Google Scholar
[72] Hiesmayr B C, Löffler W 2013 New J. Phys. 15 083036
 Google Scholar
Google Scholar
[73] Collins D, Gisin N, Linden N, Massar S, Popescu S 2002 Phys. Rev. Lett. 88 040404
 Google Scholar
Google Scholar
[74] Romero J, Leach J, Jack B, Barnett S M, Padgett M J, Franke-Arnold S 2010 New J. Phys. 12 123007
 Google Scholar
Google Scholar
[75] Gühne O, Tóth G 2009 Phys. Rep. 474 1
 Google Scholar
Google Scholar
[76] Fickler R, Krenn M, Lapkiewicz R, Ramelow S, Zeilinger A 2013 Sci. Rep. 3 1914
 Google Scholar
Google Scholar
[77] Bruß D 2002 J. Math. Phys. 43 4237
 Google Scholar
Google Scholar
[78] Gühne O, Hyllus P, Bruß D, Ekert A, Lewenstein M, Macchiavello V, Sanpera A 2002 Phys. Rev. A 66 062305
 Google Scholar
Google Scholar
[79] Agnew M, Salvail J Z, Leach J, Boyd R E 2013 Phys. Rev. Lett. 111 030402
 Google Scholar
Google Scholar
[80] Krenn M, Huber M, Fickler R, Lapkiewicz R, Ramelow S, Zeilinger A 2014 Proc. Natl. Acad. Sci. U.S.A. 111 6243
 Google Scholar
Google Scholar
[81] Choi K S, Deng H, Laurat J, Kimble H J 2008 Nature 452 67
 Google Scholar
Google Scholar
[82] Kwiat P G 1997 J. Mod. Opt. 44 2173
 Google Scholar
Google Scholar
[83] Barreiro J T, Langford N K, Peters N A, Kwiat P G 2005 Phys. Rev. Lett. 95 260501
 Google Scholar
Google Scholar
[84] Schuck C, Huber G, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 190501
 Google Scholar
Google Scholar
[85] Bozinovic1 N, Yue Y, Ren Y X, Tur M, Kristensen P, Huang H, Willner A E, Ramachandran S 2013 Science 340 1545
 Google Scholar
Google Scholar
[86] Walborn W S, Pádua S, Monken C H 2003 Phys. Rev. A 68 042313
 Google Scholar
Google Scholar
[87] Calsamiglia J, Lütkenhaus N 2001 Appl. Phys. B 72 67
 Google Scholar
Google Scholar
[88] Barreiro J T, Wei T C, Kwiat P G 2008 Nat. Phys. 4 282
 Google Scholar
Google Scholar
[89] Tiranov A, Lavoie J, Ferrier A, Goldner P, Verma V B, Nam S W, Mirin R P, Lita A E, Marsili F, Herrmann H, Silberhorn C, Gisin N, Afzelius M, Bussières F 2015 Optica 2 279
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 33197
- PDF Downloads: 103
- Cited By: 0






















 DownLoad:
DownLoad: