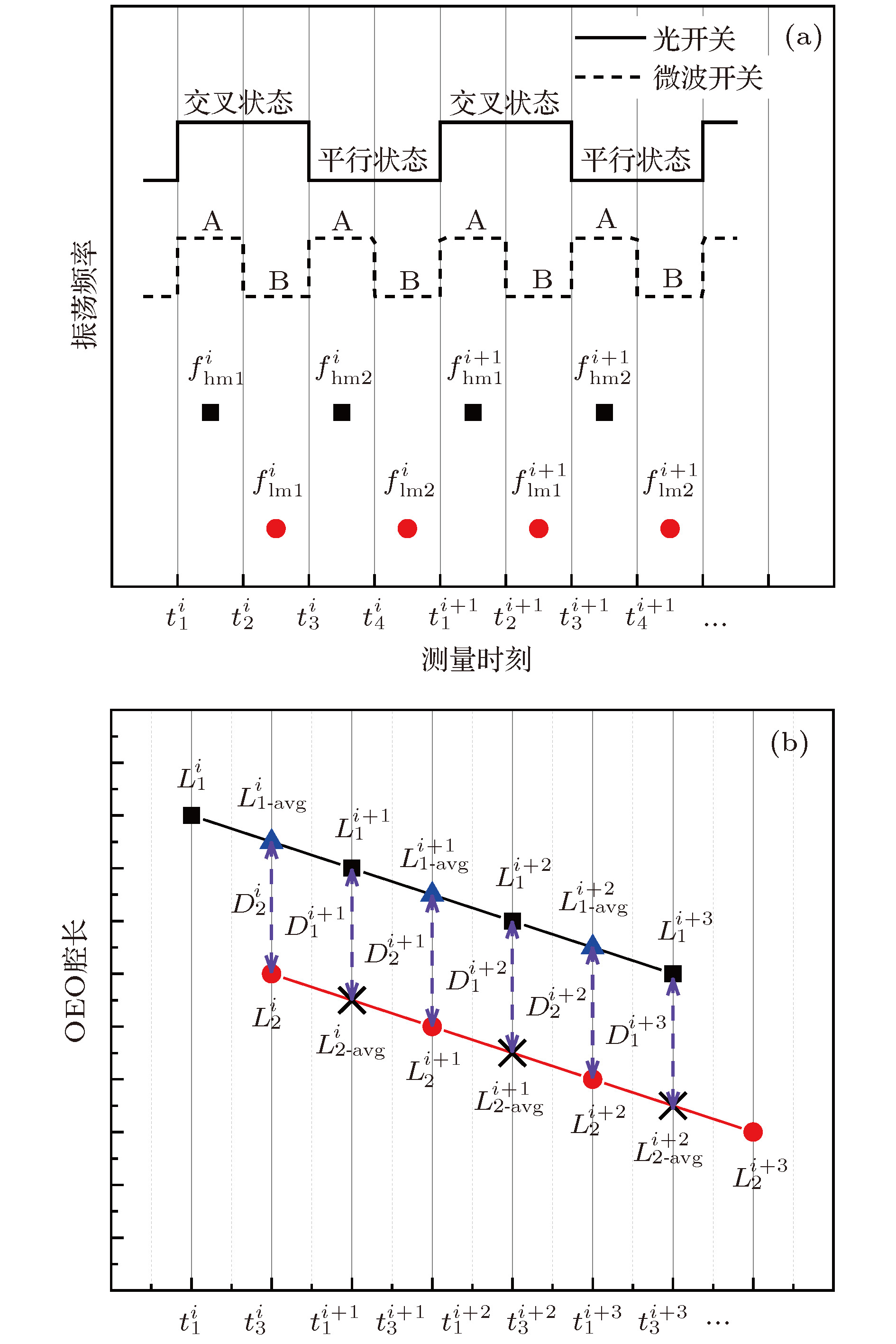
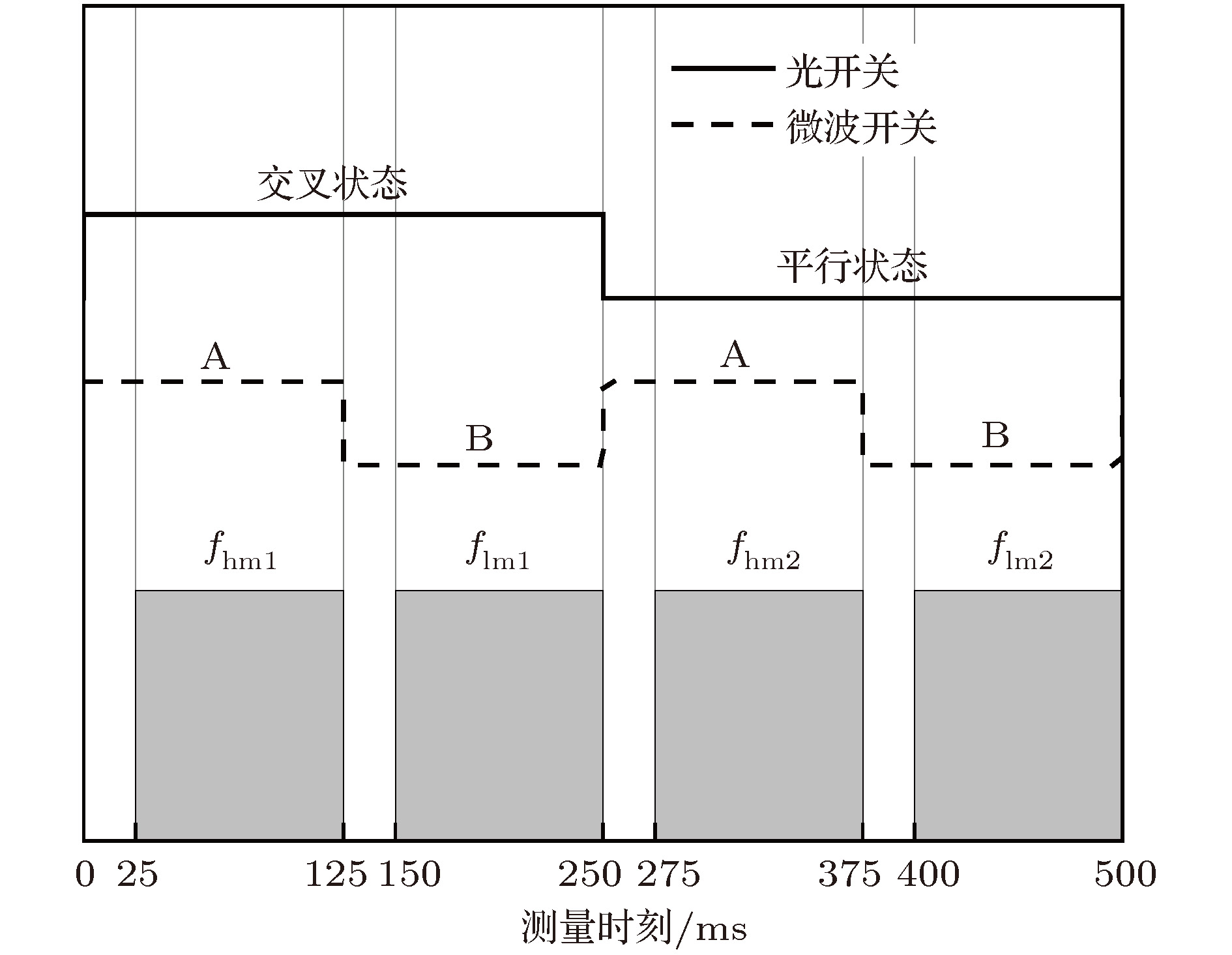
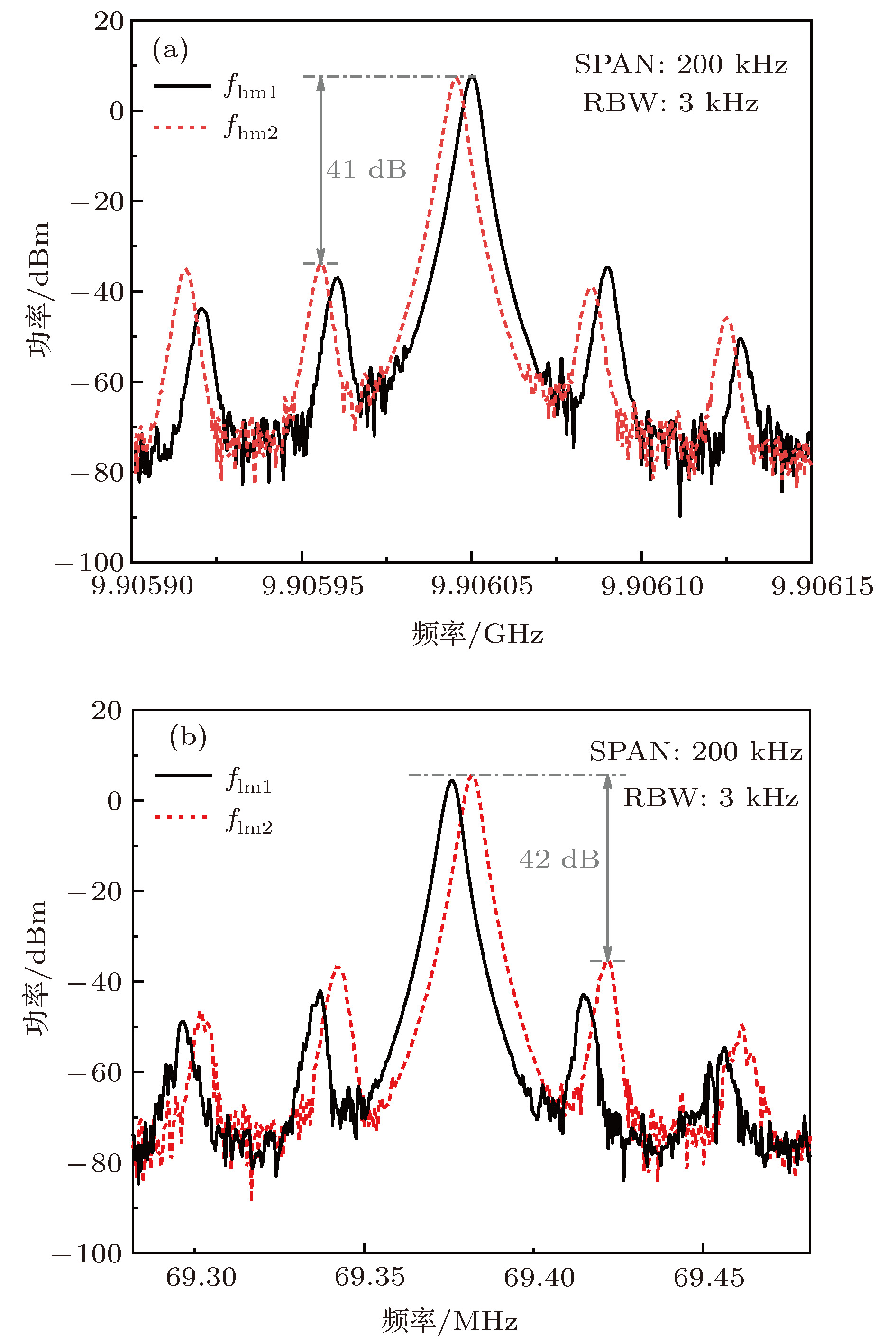
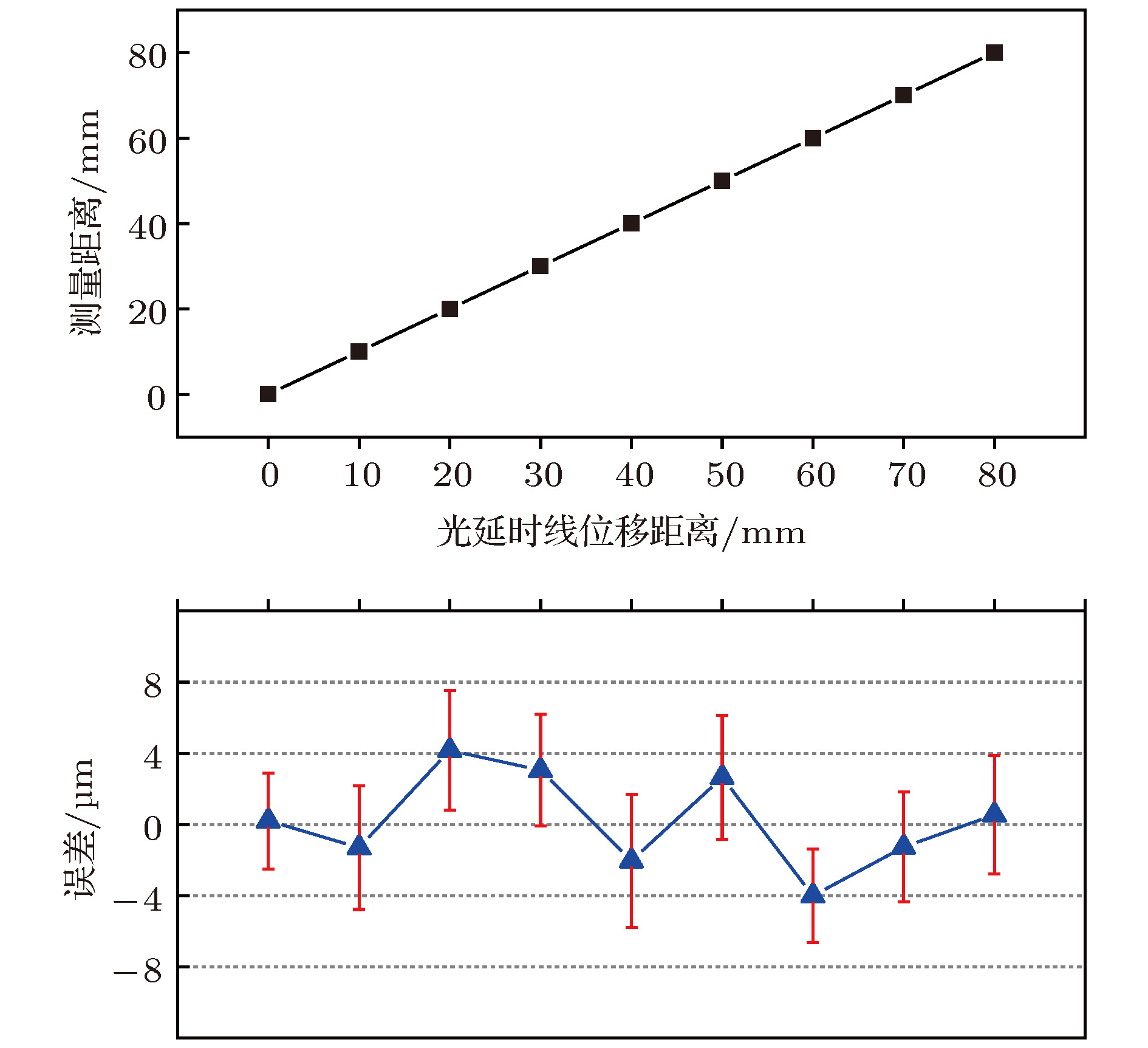
-
Absolute distance measurement plays an important role in many areas, such as aerospace and scientific research. Traditional measurement methods generally cannot meet requirements for long-range and high-precision at the same time. In this paper, an absolute distance measurement method based on alternately oscillating optoelectronic oscillator is proposed. This method places the distance to be measured in the loop of optoelectronic oscillator and takes advantage of accumulative magnification effect to achieve high accuracy. The measurement and the reference optoelectronic oscillators are established and selected by an optical switch, and a microwave switch is used to choose the high-order or low-order oscillating frequency. The high-order frequency and low-order oscillating frequency of the measurement and reference optoelectronic oscillators are measured in turn by frequency counter to calculate the loop lengths of two optoelectronic oscillators. The low-order frequencies are used to measure the fundamental frequency roughly and the high-order frequencies are used to calculate loop length precisely. Although the mode hopping occurs in the measurement process, it does not affect the loop length calculation by substituting the corresponding oscillating mode number. Note that the loop length measurement moments of two optoelectronic oscillators are different due to the switching order of optical switch and microwave switch. In order to calculate the absolute distance, which is the length difference between two optoelectronic oscillators at the same moment, the measured loop lengths should be averaged.In this way, systematic error accumulation caused by slow drift of environment can be eliminated, and this method does not need to control the length of reference optoelectronic oscillator. Meanwhile, the measurement system is simple. In the experiment, 1 km, 5 km and 8 km fibers are placed in a common part of the measurement and reference optoelectronic oscillators to simulate different long-range distances in space. A high-resolution optical delay line is placed in the measurement optoelectronic oscillator to verify the performance of the measurement system. The experimental results show that the measurement error is 3.5 μm with a 3.5 μm maximum standard deviation of each measurement distance at an emulated round trip distance of 6 km. The relative measurement accuracy reaches 5.8 × 10－10. This method provides a feasible idea for solving the technical problems of long-range and high-precision absolute distance measurement.
[1] Estler W T, Edmundson K L, Peggs G N, Parker D H 2002 CIRP Ann. 51 587
Google Scholar
[2] Tapley B D, Bettadpur S, Ries J C, Thompson P F, Watkins M M 2004 Science 305 503
Google Scholar
[3] Kim J, Lee S W 2009 Acta Astronaut. 65 1571
Google Scholar
[4] Dickey J O, Bender P L, Faller J E, Newhall X X, Ricklefs R L, Ries J G, Shelus P J, Veillet C, Whipple A L, Wiant J R, Willams J G, Yoder C F 1994 Science 265 482
Google Scholar
[5] Falaggis K, Towers D P, Towers C E 2009 Opt. Lett. 34 950
Google Scholar
[6] Yang H J, Deibel J, Nyberg S, Riles K 2005 Appl. Opt. 44 3937
Google Scholar
[7] Abouzeid A, Pollinger F, Meinershagen K, Wedde M 2009 Appl. Opt. 48 6188
Google Scholar
[8] 黑克非, 于晋龙, 王菊, 王文睿, 贾石, 吴穹, 薛纪强 2014 物理学报 63 100602
Google Scholar
Hei K F, Yu J L, Wang J, Wang W R, Jia S, Wu Q, Xue J Q 2014 Acta Phys. Sin. 63 100602
Google Scholar
[9] Ye J 2004 Opt. Lett. 29 1153
Google Scholar
[10] Lee J, Kim Y J, Lee K, Lee S, Kim S W 2010 Nat. Photon. 4 716
Google Scholar
[11] Lee J, Lee K, Lee S, Kim S W, Kim Y J 2012 Meas. Sci. Technol. 23 065203
Google Scholar
[12] Wang G, Jang Y S, Hyun S, Chun B J, Kang H J, Yan S 2015 Opt. Express 23 9121
Google Scholar
[13] Zhu Z B, Xu G Y, Ni K, Zhou Q, Wu G H 2018 Opt. Express 26 5747
Google Scholar
[14] Zhang S H, Xu Z Y, Chen B Y, Yan L P, Xie J D 2018 Opt. Express 26 9273
Google Scholar
[15] Wang J, Yu J L, Miao W, Sun B, Jia S, Wang W R, Wu Q 2014 Opt. Lett. 39 4412
Google Scholar
[16] Chen B, Yu J L, Wang J, Li T Y, Wang W R, Yu Y, Xie T Y 2016 Chin. Opt. Lett. 14 110608
Google Scholar
[17] Yao X S, Maleki L 1996 J. Opt. Soc. Am. B 13 1725
Google Scholar
[18] 贾石, 于晋龙, 王菊, 王文睿, 王子雄, 陈斌 2015 物理学报 64 154204
Google Scholar
Jia S, Yu J L, Wang J, Wang W R, Wang Z X, Chen B 2015 Acta Phys. Sin. 64 154204
Google Scholar
-
图 1 基于交替起振光电振荡器绝对距离测量的基本结构 (a)光开关处于交叉状态, 测量环振荡; (b)光开关处于平行状态, 参考环振荡
Figure 1. Basic structure of absolute distance measurement method based on alternately oscillating OEO: (a) The measurement loop oscillates with optical switch at cross state; (b) the reference loop oscillates with optical switch at parallel state.
图 2 距离测量过程 (a)光开关、微波开关切换时刻及相应的频率测量; (b) OEO1和OEO2的腔长测量及绝对距离测量
Figure 2. Distance measurement process: (a) The switching moments of optical switch and microwave switch and corresponding frequency measurement process; (b) loop length measurement of OEO1, OEO2 and the absolute distance measurement.
图 3 开关切换及频率计计数时序图
Figure 3. The switching time and frequency counting timing diagram.
图 4 测量/参考环振荡信号的频谱图 (a)高阶模式起振; (b)低阶模式起振
Figure 4. RF spectrum of oscillating frequencies of measurement/reference loop: (a) With OEO oscillating at high-order mode; (b) with OEO oscillating at low-order mode.
图 5 长光纤为5 km光延时线在0 mm位置时的测量结果 (a) OEO1和OEO2起振频率测量值; (b) OEO1和OEO2的腔长及待测距离测量结果
Figure 5. Measurement results at 0 mm position of optical delay line with 5 km fiber: (a) Oscillating frequencies of OEO1 and OEO2; (b) loop lengths of OEO1 and OEO2, and distance measurement results.
图 6 长光纤为5 km时测量距离与光延时线位移距离的关系
Figure 6. The relationship between measured distance and position variation of optical delay line with 5 km fiber.
图 7 测量距离与光延时线位移距离的关系 (a) 1 km长光纤; (b) 8 km长光纤
Figure 7. The relationship between measured distance and position variation of optical delay line: (a) With 1 km fiber; (b) with 8 km fiber.
-
[1] Estler W T, Edmundson K L, Peggs G N, Parker D H 2002 CIRP Ann. 51 587
Google Scholar
[2] Tapley B D, Bettadpur S, Ries J C, Thompson P F, Watkins M M 2004 Science 305 503
Google Scholar
[3] Kim J, Lee S W 2009 Acta Astronaut. 65 1571
Google Scholar
[4] Dickey J O, Bender P L, Faller J E, Newhall X X, Ricklefs R L, Ries J G, Shelus P J, Veillet C, Whipple A L, Wiant J R, Willams J G, Yoder C F 1994 Science 265 482
Google Scholar
[5] Falaggis K, Towers D P, Towers C E 2009 Opt. Lett. 34 950
Google Scholar
[6] Yang H J, Deibel J, Nyberg S, Riles K 2005 Appl. Opt. 44 3937
Google Scholar
[7] Abouzeid A, Pollinger F, Meinershagen K, Wedde M 2009 Appl. Opt. 48 6188
Google Scholar
[8] 黑克非, 于晋龙, 王菊, 王文睿, 贾石, 吴穹, 薛纪强 2014 物理学报 63 100602
Google Scholar
Hei K F, Yu J L, Wang J, Wang W R, Jia S, Wu Q, Xue J Q 2014 Acta Phys. Sin. 63 100602
Google Scholar
[9] Ye J 2004 Opt. Lett. 29 1153
Google Scholar
[10] Lee J, Kim Y J, Lee K, Lee S, Kim S W 2010 Nat. Photon. 4 716
Google Scholar
[11] Lee J, Lee K, Lee S, Kim S W, Kim Y J 2012 Meas. Sci. Technol. 23 065203
Google Scholar
[12] Wang G, Jang Y S, Hyun S, Chun B J, Kang H J, Yan S 2015 Opt. Express 23 9121
Google Scholar
[13] Zhu Z B, Xu G Y, Ni K, Zhou Q, Wu G H 2018 Opt. Express 26 5747
Google Scholar
[14] Zhang S H, Xu Z Y, Chen B Y, Yan L P, Xie J D 2018 Opt. Express 26 9273
Google Scholar
[15] Wang J, Yu J L, Miao W, Sun B, Jia S, Wang W R, Wu Q 2014 Opt. Lett. 39 4412
Google Scholar
[16] Chen B, Yu J L, Wang J, Li T Y, Wang W R, Yu Y, Xie T Y 2016 Chin. Opt. Lett. 14 110608
Google Scholar
[17] Yao X S, Maleki L 1996 J. Opt. Soc. Am. B 13 1725
Google Scholar
[18] 贾石, 于晋龙, 王菊, 王文睿, 王子雄, 陈斌 2015 物理学报 64 154204
Google Scholar
Jia S, Yu J L, Wang J, Wang W R, Wang Z X, Chen B 2015 Acta Phys. Sin. 64 154204
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 13419
- PDF Downloads: 123
- Cited By: 0
