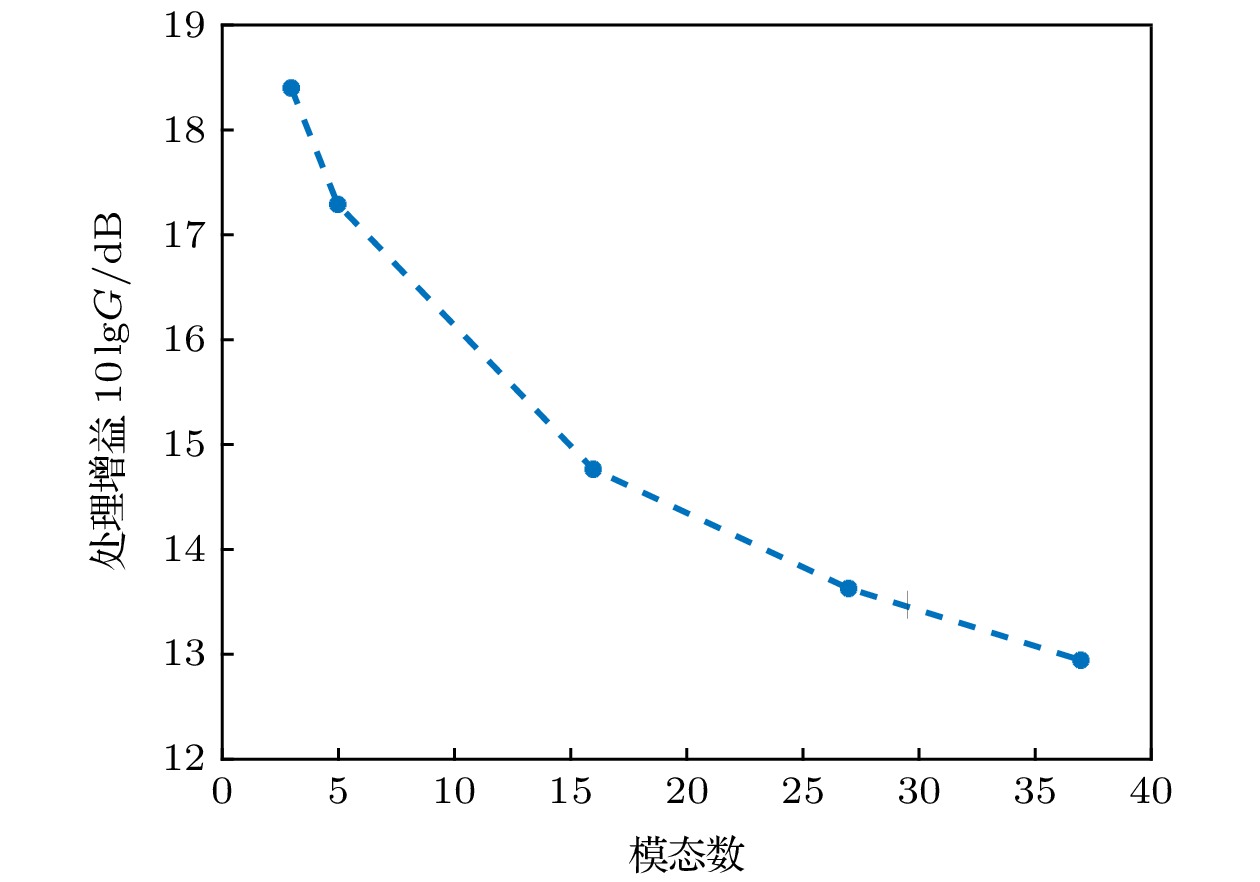
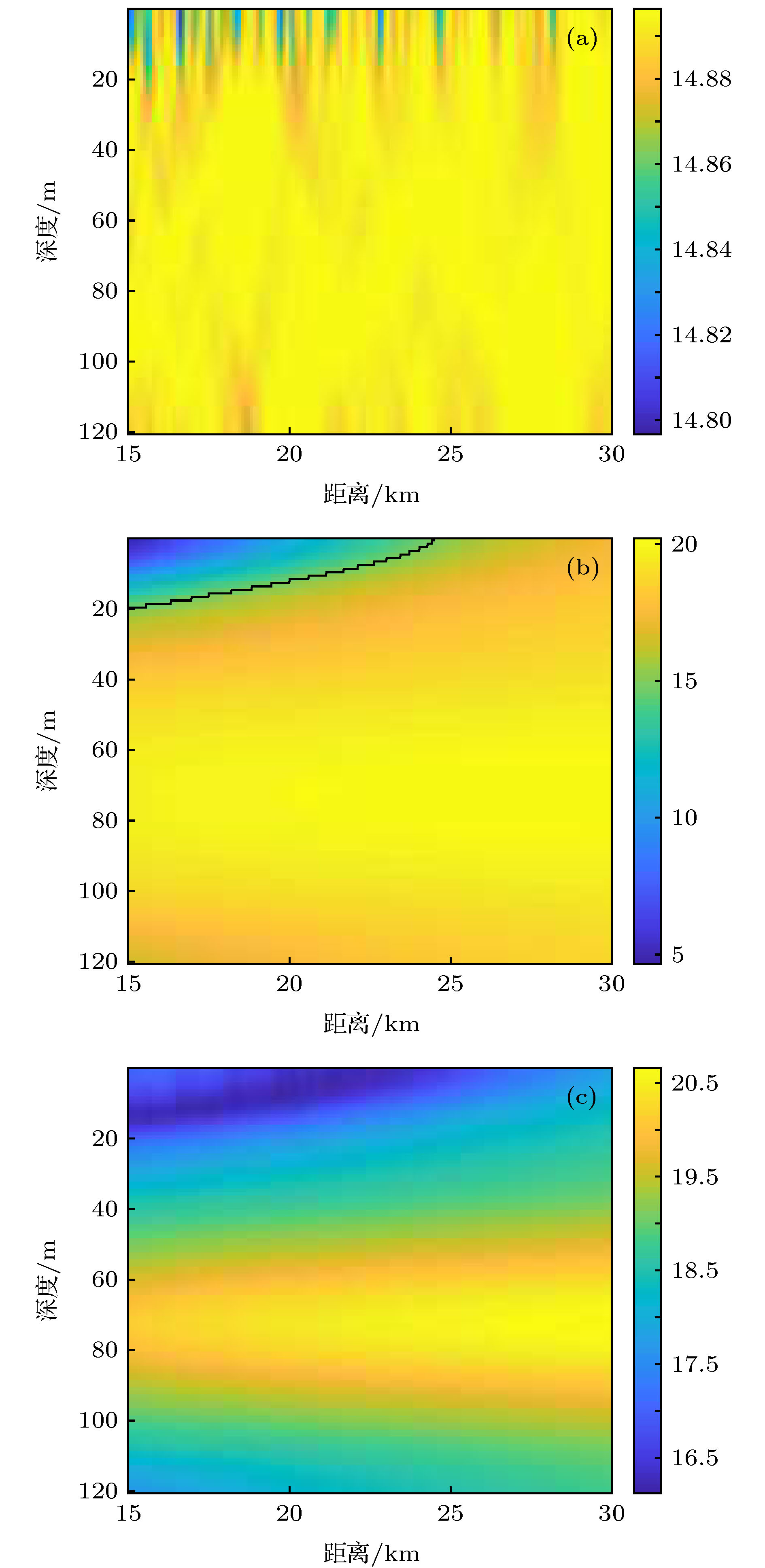
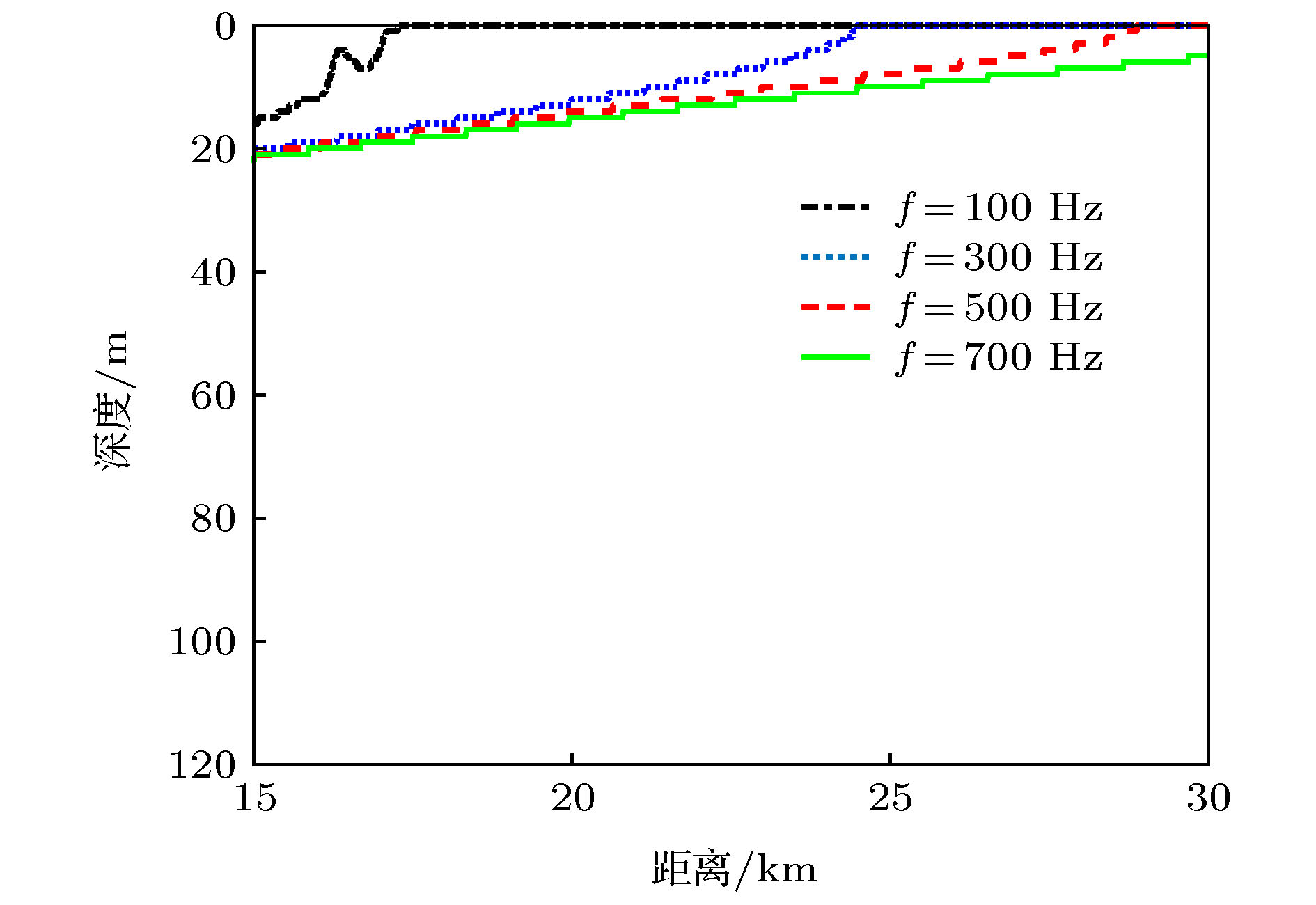
-
In this paper, the modal space detector (MSD) is investigated in shallow water environment when utilizing a vertical linear array. The processing gain of the MSD is derived, and the result demonstrates that the processing gain of the MSD degrades when the number of the propagated normal modes excited by the underwater acoustic source increases, and therefore the detection performance of the MSD decreases. By exploiting the orthogonality among the modal depth functions, the MSD can be decomposed into a group of modal subspace detectors (MSSDs). The processing gains of these MSSDs are derived as well and it is found out that the processing gain of a MSSD is in direct proportion to its corresponding modal attenuation coefficients. By designing a group of weighting coefficients based on the mode attenuation law, a weighted modal subspace detector (WMSSD) is proposed to alleviate the degradation of the processing gain processing of the MSD. We analyze the influences of acoustic source locations and sound velocity profiles (SVPs) on the detection performance of the WMSSD theoretically, and verify the theoretical analyses by comparing its processing gain with the MSD in simulation experiments. The results show that the WMSSD presents various processing gains versus different acoustic source locations. In the waveguide having a negatively-gradient SVP, there exists a ‘weak detection area’ for the WMSSD, that is, the processing gain of the WMSSD is smaller than that of the MSD when the acoustic source locations are close to sea surface. The reason is because there are inversion points on the lower-order modal depth functions and the depths of the inversion points are close to sea surface. In other most areas, the processing gain of the WMSSD is larger (even remarkably larger) than that of the MSD. In the waveguide having a positively-gradient SVP, due to the phenomenon that the modal inversion points of the lower-order modal depth functions are near sea floor, there is a contrary consequence, that is, the ‘weak detection area’ is close to sea floor. And meanwhile the WMSSD outperforms the MSD in other most areas as well. There are no modal inversion points in the waveguide having a constant SVP, and therefore the WMSSD always outperforms the MSD.
-
Keywords:
- modal space detection /
- modal attenuation coefficient /
- processing gain /
- modal inversion point
[1] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
Google Scholar
[2] Sha L, Nolte L W 2005 J. Acoust. Soc. Am. 117 1942
Google Scholar
[3] Sha L, Nolte L W 2006 IEEE J. Oceanic Eng. 31 345
Google Scholar
[4] 刘宗伟, 孙超, 易锋, 郭国强, 向龙凤 2014 声学学报 3 309
Liu Z W, Sun C, Yi F, Guo G Q, Xiang L F 2014 Acta Acust. 3 309
[5] 刘宗伟, 孙超, 吕连港 2015 声学学报 5 665
Liu Z W, Sun C, Lv L G 2015 Acta Acust. 5 665
[6] Scharf L L, Friedlander B 1993 IEEE Trans. Signal Process. 42 2146
[7] Krishna K M, Anand G V 2009 IEEE OCEANS Biloxi, USA, October 26−29, 2009 p1
[8] Hari V N, Anand G V, Premkumar A B, Madhukumar A S 2011 IEEE OCEANS Santander, Spain, June 6−9, 2011 p1
[9] Hari V N, Anand G V, Nagesha P V, Nagesha P V, Premkumar A B 2012 Proceedings of the 20th European Signal Processing Conference Bucharest, Romania, August 27−31, 2012 p1334
[10] Hari V N, Anand G V, Premkumar A B 2013 Digit. Signal Process. 23 1645
Google Scholar
[11] 李明杨, 孙超, 邵炫 2014 物理学报 20 204302
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 20 204302
Google Scholar
[12] Li M, Sun C, Willett P 2017 IEEE J. Oceanic Eng. 99 1
[13] Kong D Z, Sun C, Li M Y, Liu X H, Xie L 2019 IEEE Access 7 79644
Google Scholar
[14] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 物理学报 68 174301
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
Google Scholar
[15] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp258−263
[16] 张仁和 1979 声学学报 2 16
Zhang R H 1979 Acta Acust. 2 16
[17] Wang Q, Zhang RH 1990 J. Acoust. Soc. Am. 87 633
Google Scholar
[18] 汪德昭, 尚尔昌2013 水声学(第二版) (北京: 科学出版社) pp92−94
Wang D Z, Shang E C 2013 Underwater Acoustics (Vol. 2) (Beijing: Science Press) pp92−94 (in Chinese)
[19] 斯蒂芬Kay著 (罗鹏飞, 张文明译) 2011 统计信号处理基础 (北京: 电子工业出版社) 第573−574页
Kay S M (translated by Luo P F, Zhang W M) 2011 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp573−574 (in Chinese)
[20] Morgan D R, Smith T M 1990 J. Acoust. Soc. Am. 87 737
Google Scholar
-
图 1 浅海波导环境及其相关参数
Figure 1. The shallow water waveguide and its environmental parameters.
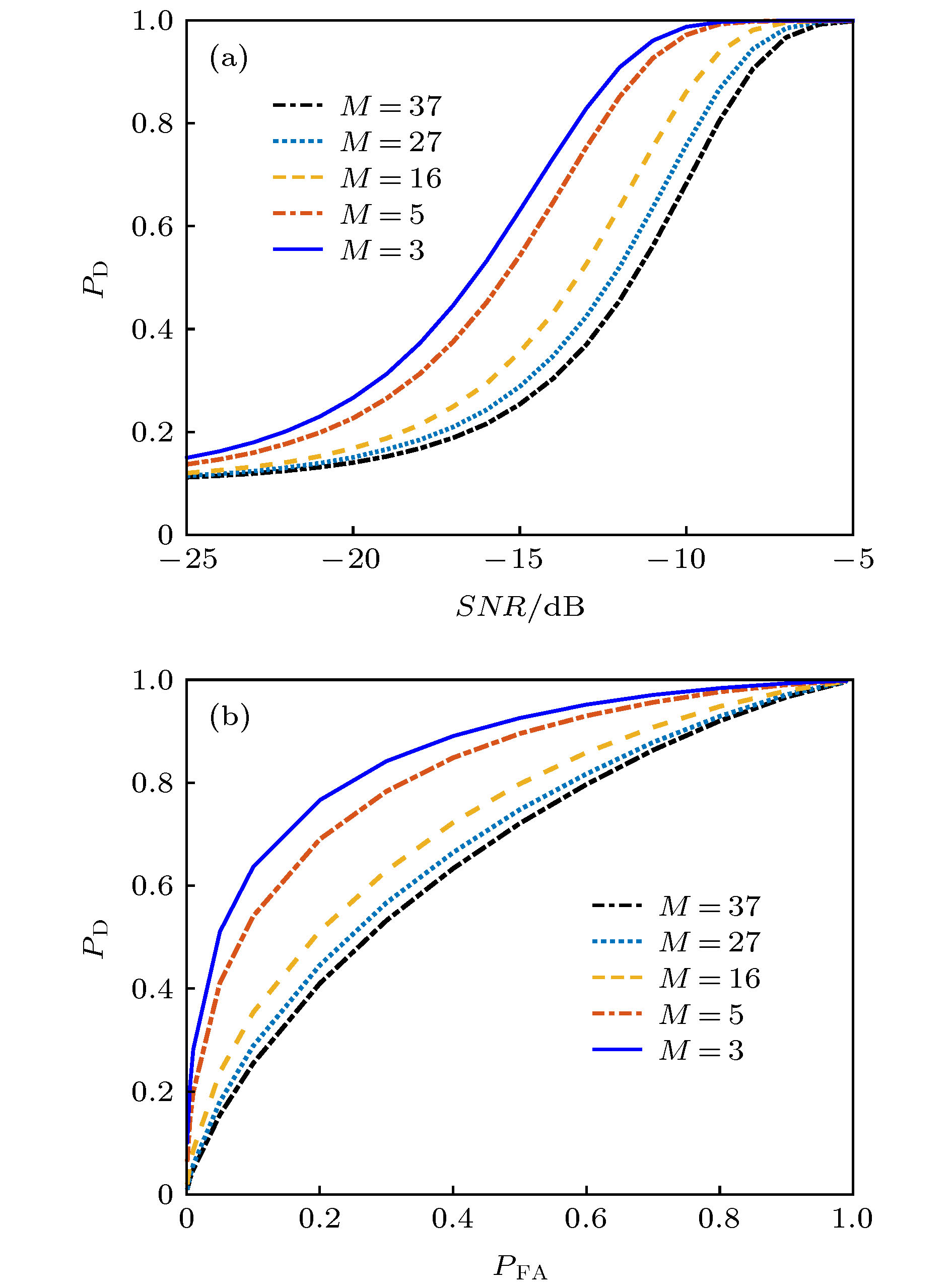
图 2 不同传播模态数下MSD的检测性能曲线 (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{ dB}}$ Figure 2. Detection performance curves of the MSD under various numbers of normal modes: (a) Probabilities of detection versus SNRs,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ .
图 3 MSD的处理增益随模态数的变化曲线
Figure 3. The processing gains of the MSD versus the numbers of normal modes.
图 4 各阶MSSD处理增益随阶数的变化
Figure 4. The processing gains of MSSD versus the orders of normal modes.
图 5 MSD, WMSSD, OWMSSD的检测性能曲线, f = 100 Hz (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{dB}}$ Figure 5. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 100 Hz: (a) Probabilities of detection versus SNR,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ .
图 6 MSD, WMSSD, OWMSSD的检测性能曲线, f = 300 Hz (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{dB}}$ Figure 6. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 300 Hz: (a) Probabilities of detection versus SNR,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ .
图 7 MSD, WMSSD, OWMSSD的处理增益随声源位置的变化, f = 300 Hz (a) MSD; (b) WMSSD; (c) OWMSSD
Figure 7. The processing gains of the MSD, WMSSD and OWMSSD versus acoustic source locations with f = 300 Hz: (a) MSD; (b) WMSSD; (c) OWMSSD.
图 8 各阶模态函数及其反转点深度, f = 300 Hz (a) 波导环境中的各阶模态函数分布; (b) 各阶模态函数的反转点深度
Figure 8. The modal depth functions and their turning-depths with f = 300 Hz: (a) Each modal depth function in the waveguide; (b) the turning-depth of each modal depth function.
图 9 各阶MSSD的加权系数与处理增益, f = 300 Hz, 声源距离15 km (a)声源深度10 m; (b) 声源深度80 m
Figure 9. The weighting coefficients and the processing gains of the MSSD with f = 300 Hz and source range of 15 km: (a) Source depth of 10 m; (b) source depth of 80 m.
图 10 不同频率时临界深度随距离的变化图
Figure 10. The critical depths versus ranges under various frequencies.
图 11 各阶MSSD归一化的加权系数与处理增益, f = 300 Hz, 声源深度10 m, 声源距离25 km
Figure 11. The weighting coefficients and the processing gains of the MSSD with f = 300 Hz, source depth of 10 m and source range of 25 km.
图 12 等声速剖面与正梯度声速剖面图
Figure 12. Constant sound velocity profile (SVP) and positive gradient SVP.
图 13 各阶模态函数的反转深度, f = 300 Hz
Figure 13. The turning-depth of each modal depth function with f = 300 Hz.
图 14 两种声速剖面波导中的各阶模态函数, f = 300 Hz (a) 等声速剖面; (b) 正梯度声速剖面
Figure 14. Each modal depth function in the two kinds of waveguides with f = 300 Hz: (a) Constant SVP; (b) positive gradient SVP.
图 15 两种声速剖面下, 不同声源位置处的WMSSD处理增益, f = 300 Hz (a)等声速剖面; (b) 正梯度声速剖面
Figure 15. The processing gains of the WMSSD versus acoustic source locations with f = 300 Hz: (a) Constant SVP; (b) positive gradient SVP.
-
[1] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
Google Scholar
[2] Sha L, Nolte L W 2005 J. Acoust. Soc. Am. 117 1942
Google Scholar
[3] Sha L, Nolte L W 2006 IEEE J. Oceanic Eng. 31 345
Google Scholar
[4] 刘宗伟, 孙超, 易锋, 郭国强, 向龙凤 2014 声学学报 3 309
Liu Z W, Sun C, Yi F, Guo G Q, Xiang L F 2014 Acta Acust. 3 309
[5] 刘宗伟, 孙超, 吕连港 2015 声学学报 5 665
Liu Z W, Sun C, Lv L G 2015 Acta Acust. 5 665
[6] Scharf L L, Friedlander B 1993 IEEE Trans. Signal Process. 42 2146
[7] Krishna K M, Anand G V 2009 IEEE OCEANS Biloxi, USA, October 26−29, 2009 p1
[8] Hari V N, Anand G V, Premkumar A B, Madhukumar A S 2011 IEEE OCEANS Santander, Spain, June 6−9, 2011 p1
[9] Hari V N, Anand G V, Nagesha P V, Nagesha P V, Premkumar A B 2012 Proceedings of the 20th European Signal Processing Conference Bucharest, Romania, August 27−31, 2012 p1334
[10] Hari V N, Anand G V, Premkumar A B 2013 Digit. Signal Process. 23 1645
Google Scholar
[11] 李明杨, 孙超, 邵炫 2014 物理学报 20 204302
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 20 204302
Google Scholar
[12] Li M, Sun C, Willett P 2017 IEEE J. Oceanic Eng. 99 1
[13] Kong D Z, Sun C, Li M Y, Liu X H, Xie L 2019 IEEE Access 7 79644
Google Scholar
[14] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 物理学报 68 174301
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
Google Scholar
[15] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp258−263
[16] 张仁和 1979 声学学报 2 16
Zhang R H 1979 Acta Acust. 2 16
[17] Wang Q, Zhang RH 1990 J. Acoust. Soc. Am. 87 633
Google Scholar
[18] 汪德昭, 尚尔昌2013 水声学(第二版) (北京: 科学出版社) pp92−94
Wang D Z, Shang E C 2013 Underwater Acoustics (Vol. 2) (Beijing: Science Press) pp92−94 (in Chinese)
[19] 斯蒂芬Kay著 (罗鹏飞, 张文明译) 2011 统计信号处理基础 (北京: 电子工业出版社) 第573−574页
Kay S M (translated by Luo P F, Zhang W M) 2011 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp573−574 (in Chinese)
[20] Morgan D R, Smith T M 1990 J. Acoust. Soc. Am. 87 737
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6355
- PDF Downloads: 50
- Cited By: 0
